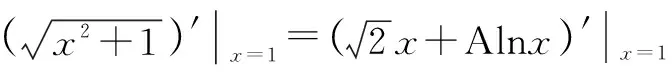活跃在证明题中的构造局部不等式法
2020-06-06朱小扣
朱小扣
(安徽省无为第三中学城北校区 238300)
笔者发现构造局部不等式在证明竞赛题与数学通讯等期刊的征解题中有着重要的作用.本文将从四个角度去构造局部不等式,以期抛砖引玉.
一、利用切线法构造局部不等式
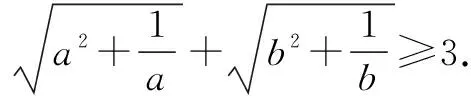

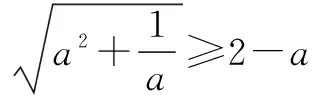
⟺(2a-1)2≥0 (0 ①+②即证. 用切线法可以解决很多题目,如数学通讯问题332: 例2(数学通讯问题332)已知正数x,y,z满足xy+yz+zx≤3,求证: 同理: ①+②+③得: 令a=xy,b=yz,c=zx,则问题转化为在a+b+c≤3的条件下,求证: 由切线法得只需证: ⟺4≥(1+a)(3-a)⟺(a-1)2≥0. ④+⑤+⑥得: 故原命题得证. 上述例题用割线法可以很快解决.又如数学通讯问题399: 例4(数学通讯399问题)已知△ABC,记BC=a,CA=b,AB=c,求证: 原命题等价于: 下面先证明: 三式相加得: 故原不等式得证. 故只需证明: 故原不等式得证. 例6 (数学通讯398问题)已知正数a,b,c满足a+b+c≤12,求证:abc≤2a+5b+10c. 当且仅当a=5,b=4,c=3时取等号. 即证. 本题证明是笔者采用文[2]中类似的构造方法写出来的,非常令人不解的是为什么这样构造局部不等式,原因如下: 先a=5,b=4,c=3时取等号, 此法还可以解决很多类似的题目. 例7(数学通讯390问题)已知正数a,b,c,d且满足abcd=1,求证: 于是,f′(x)单调递减,而f′(1)=0 易得,当x∈(0,1)时,f′(x)>0,x∈(1,+)时,f′(x)<0. ⟹f(x)≤f(1)=0,即证①式. 四式相加,即证. 此种方法有别于切线法的“以直代曲”,这是“以曲代曲”.又如: 例8(2004年波兰奥林匹克)已知正数a,b,c且满足a2+b2+c2=1,求证: 以下证明: 故①式恒成立.故: 三式相加,即证. 类似地,还可以解决很多不等式竞赛题,如:2005年摩尔多瓦竞赛题等. 以上阐述了四种构造局部不等式证明试题的方法,正是”花开四朵,各自妖娆.” 当然,能用构造局部不等式去证明的题目可能远不止这四种,希望大家能继续研讨升级.
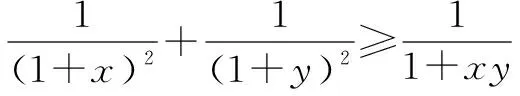





二、利用割线法构造局部不等式


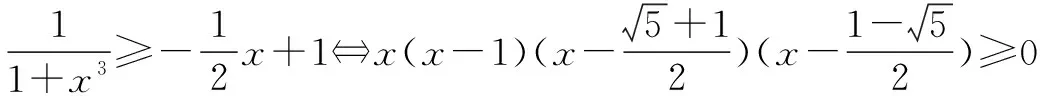








三、利用均值不等式构造局部不等式
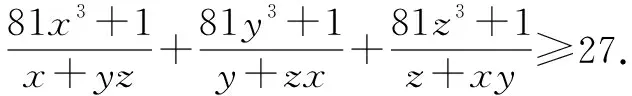





四、利用支撑函数构造局部不等式