解压轴题:见微知著 大胆设想
2020-06-06许银伙杨苍洲
数理化解题研究 2020年16期
许银伙 杨苍洲
(1.福建省泉州外国语学校 362000;2.福建省泉州第五中学 362000)
作为高考函数压轴题,通常都是情境较新颖、难度较大的数学问题,因此问题的解答,除了必须综合运用各种数学思想、方法和知识外,还需要细心观察,见微知著,调动自身的解题经验,大胆设想,创新解法,才有可能突破问题的解答瓶颈,提升自己的解题能力.

(1) 试讨论函数f(x)的单调性;
(2)证明:f(x)≥g(x).


观察到:h(1)=0,h′(1)=0,思考:h(1)应该是函数h(x)的最小值,预测当x∈(1,+)时,h′(x)≥0;当x∈(0,1)时,h′(x)≤0.下证明之:
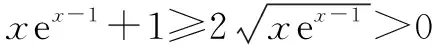

综上得:h(x)≥0对x>0恒成立,即f(x)≥g(x)恒成立.
反思与评注问题(2)的解决主要靠观察与猜想,见微知著.
1.令h(x)=f(x)-g(x),观察到:h(1)=0,h′(1)=0,思考:h(1)应该是函数h(x)的最小值.

3.当x∈(0,1)时和当x∈(1,+)时,在h′(x)中分别把ex-1用1代入放缩和用消去ex-1是本题解答的最大“亮点”.
例题2(2016年东北三省四市联合体试题理科)已知函数f(x)=e1-xcosx.



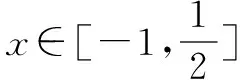

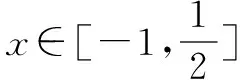

2.针对含多个超越函数的不等式的证明,通常有两种方法:(1)通过放缩减少超越函数式的个数,如例1.(2)引入切线,转化成两个不等式加以证明.





反思与评注1.本题的解决有两个难点:


例题4 (2018全国卷(Ⅲ)理科21)已知函数f(x)=(2+x+ax2)ln(1+x)-2x.
(1)若a=0,证明:当-1
(2) 若x=0是f(x)的极大值点,求a.
分析与解(1)略.




