具有Logistic增长的SIRS传染病模型的稳定性及最优控制分析

许云霞，雷学红

(凯里学院 理学院，贵州 凯里 556011)

当前，传染病严重地威胁着人类的健康及生命，对人类生存和国民经济造成了不可估量的损失，因此传染病的研究一直是医学界和生态环境学界关注的主要对象.传染病动力学的建模与分析是研究传染病传播规律的重要方法.自从Kermack与Mckendrick[1]创建了SIR仓室模型后，人们在此基础上做了大量的研究工作.许多学者利用动力学原理建立了SIR、SIS、SIERS等不同的传染病模型.传染率是研究传染病的一个重要的因素，人们根据传染率的特点提出了不同形式的传染率模型.在经典的传染病模型中，常见的是标准型或双线性传染率[2-3].近年来，许多不同形式的非线性传染率相继被引入[4-9],其中，文献[7]提出了发生率为Sg(I)的时滞型传染病模型.本文在此基础上研究了具有发生率为f(S,I)的时滞型传染病模型，具体模型如下:

(1)

其中：S(t)、I(t)、R(t)分别表示在t时刻的易感者、感染者、恢复者的数量，且易感者按照Loglistic方式增长，内禀增长率为r，K为所容纳的最大容量口的常数，μ、α分别表示人群的自然死亡率、因病死亡率，ε、d分别表示为相应的转化率，f(S,I)为疾病的非线性接触率函数；时滞τ表示为潜伏期；e-μτf(S(t-τ)、I(t-τ))表示在t-τ到时间t段时间内感染者的数量.由生态学的意义可知，所有的参数均为非负数.系统(1)满足如下初始条件：

S(θ)=φ1(θ),I(θ)=φ2(θ),R(θ)=φ3(θ);φi(θ)≥0,θ∈[-τ,0].

(2)

(H1)f(0,I)=f(S,0)=0.对∀(S,I)∈Ω，有f(S,I)>0；

1 基本再生数及平衡点的存在性

定理1设(S(t),I(t),R(t))是系统(1)满足条件(2)的解，对任意的t≥0时，其解非负且有界.

证明(S(t),I(t),R(t))是系统(1)满足条件(2)的解，有:

I(t)≥φ2(0)e-(μ+α+ε)t≥0;R(t)≥φ3(0)e-(μ+d)t≥0，

令y(t)=S(t)+e-μτI(t+τ)+R(t)；y′(t)+εy(t)≤(r+μ)S(t)-rS2(t)/K.

有：y′(t)+εy(t)≤m，(m=K(r+μ)2/4r)，即:

因此系统(1)的解有界.

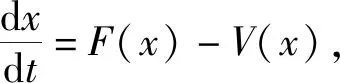
则：

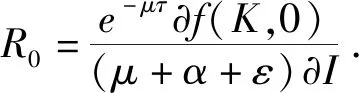
(3)

e-μτf(S(t),I(t))-(μ+α+ε)I(t)=0，

(4)

I(t)-(d+μ)R(t)=0.

(5)

(d+μ)rS2(t)-r(d+μ)KS(t)+[(μ+α+ε)(d+μ)eμτ-dε]KI(t)=0，

令：

定理2在假设条件(H1)～(H3),当R0≤1时，对于任意τ≥0，系统(1)在E0处局部渐近稳定的；当R0>1时，E0是不稳定的.

证明系统(1)在E0处的特征方程为：

显然，方程的根：λ1=-r<0，λ2=-d<0.其它的根由下面的方程决定：

(6)

假设Re(λ)≥0，代入式(6)可得：

(7)

当R0≤1时，由式(7)可知Re(λ)<0，与假设矛盾，故Re(λ)<0.系统(1)在E0处局部渐近稳定的.

定理3在假设条件(H1)～(H3)，当R0≤1时，系统(1)的无病平衡点E0(K,0,0)在Ω内全局渐近稳定的.

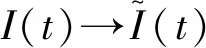
证明令lt=(S(t+θ),I(t+θ),R(t+θ))，θ∈[-τ,0].构建如下函数：

则

v′(lt)=I′(t)+e-μτf(S(t),I(t))-e-μτf(S(t-τ),I(t-τ))=e-μτf(S(t),I(t))-(μ+α+ε)I(t)

在无病平衡点E0(K,0,0)处，

则由假设条件(H2)可知，e-μτf(K,0)=0.得:

在E0处，I→0+，现对I取极限，有:

因此，当R0≤1时，有v′(lt)≤0.且在点E0(K,0,0)，v′(lt)=0.由Lyapunov-LaSalle不变原理得，系统(1)在E0(K,0,0)点是全局渐近稳定的.

2 特殊情形的最优控制策略分析

(8)

满足初始条件(2).因模型(8)的控制函数u1(t)、u2(t)随时间而变化.现实中，人们希望通过采取措施取得对疾病最优控制效果，把感染人数降到最低，花费的费用最低.故提出如下目标函数[12]：

(9)

(10)

控制条件为：U={(u1,u2)∈L1(t0,tf)|0≤u1,u2≤1}.为了寻找最优解，令Lagrange函数[13-15]:

(11)

定义该控制问题的哈密尔顿函数为:

(12)

λi(i=1,2,3)为系统的伴随变量，fi为系统(12)中第i方程的右端函数，应用Pontryagin最大值原理可以推导出最优控制的必要条件.

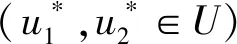
(13)

(14)

证明根据时滞状态下的Pontryagin极大值原理[14-16]，得到如下的伴随方程和横截条件:

利用最优控制性条件得：

因为0≤ui(t)≤1(i=1,2)，利用控制空间U，有以下几种情况：

故最优控制的特征为式(13)、式(14).

3 数值仿真

下面运用MATLAB软件和龙格-库塔方法进行数值模拟和仿真，其模型参数和仿真参数如下：

r=0.5,K=300,β=0.001;α1=0.02,d=0.03,τ=1,μ=0.04,α=0.02,ε=0.03;S(0)=820,I(0)=110,R(0)=70;B1=100,B2=500,u1=0-1,u2=0-1,t0=0,tf=200.

在数值模拟中，选取接种变量u1、治疗策略u2的取值范围也为0～1，表示采取有效策略的程度.τ=1表示疾病发生1d后立即引起社会的关注，且采取有效的接种和治疗措施.分别采取3种情况(①不采取任何有效措施，即u1=u2=0；②仅采取有效的接种治疗，即u1≠0,u2=0；③采取有效的接种和治疗措施，即u1≠0,u2≠0)下进行比较易感者S(t)、感染者I(t)、恢复者R(t)随着时间t变化趋势图(见图1).

图1中易感者S(t)在2种情况下都迅速下降到平衡状态，在没有控制条件下比在控制条件下更先达到平衡位置，但感染者的数量在控制条件下比没有控制条件下明显的减少.图2中感染者I(t)在没有控制条件下出现迅速上升后又下降达到平衡位置.在控制条件下I(t)迅速下降到平衡位置.所用时间也相对短一些，说明在最优控制下的感染者的数量比没有控制的数量明显降低.图3中，显然在控制条件下恢复者R(t)的量迅速上升达到新的平衡位置，在没有控制条件下恢复者R(t)的量仅能保持在一个比较少的量中保持平衡.