计及需求响应和蓄电池综合损耗的微电网优化调度
2020-06-06尹立敏蒋家祥杨镇达倪明伟
尹立敏,王 琳,雷 刚,蒋家祥,杨镇达,倪明伟
(1.东北电力大学电气工程学院,吉林 吉林 132012;2.国网吉林省电力公司辽源分公司,吉林 辽源 136200)
近年来,飞速发展的经济在改善人民生活质量的同时,对电力能源的要求也越来越高[1].化石能源的消耗量飞速增长加剧了全球能源枯竭的形势,分布式发电技术的发展,可以缓解传统化石能源的枯竭问题和环境问题.分布式发电(Distributed Generation,DG)具有对环境友好、装配便捷、安全可靠等优势[2].然而,由于分布式发电受环境条件的波动性和随机性较大,对主网的安全稳定性造成威胁[3].微电网可以对分布式发电进行整合管理,在保障系统安全可靠性的前提下,提高了清洁能源的利用率.并网型微电网管理系统要在联络线功率约束范围内调整DG的出力.不仅如此,目标函数还要充分考虑微电网与大电网的交互成本,而在电力市场环境中,随着电能需求的日益增长,负荷峰谷差也被逐渐拉大,使得需求响应(Demand Response,DR)得到广泛的关注,DR作为实现需求侧管理的主要措施[4],可以引导电力用户对市场电价信号或者激励机制做出响应,从而改变用户电力消费习惯.在DR参与的项目中,根据不同的响应机制,可分为采用负荷控制补偿激励机制的激励型需求响应[5]和采用负荷价格弹性电价的价格型需求响应[6-8]两种方式,参与电力市场运行[9].通过改善负荷曲线的分布,优化资源配置,是应对可再生能源波动性、不确定性的有效途径.所以研究需求响应对微电网成本优化的影响,对并网型微电网的日前经济运行优化有着重要的意义.
关于需求管理侧参与优化微电网经济运行的问题,国内外学者就此问题进行了大量研究.文献[10]在考虑大电网分时电价的基础上引入负荷管理,建立了含有风光燃储家庭型微电网优化调度模型,降低了用户的购电费用,也实现了可中断负荷的零削减,提高了用户的舒适度.文献[11]提出了微电网双层优化模型,将需求侧响应层和微网层采用源荷互动方式对需求响应层的负荷曲线进行优化,不仅改善了清洁能源利用率,也降低了可控微源平稳性指标,进一步提高了微网运行的综合经济效益.文献[12]在分时电价机制下,以电网交换量最小引入到目标函数中,针对光伏微电网优化运行调度问题进行了研究.文献[13]以用户侧用电成本、空调与热水器的舒适度作为优化目标,验证了优化模型实用性,有效地降低了用电成本.虽然上述研究针对可转移负荷、可削减负荷进行相关分析,但所研究负荷只考虑两种情况,即整体平移或者不平移,在实际工程运用上具有片面性.
另外,由于微电网中风光出力的波动性和不稳定性,作为微电网中平衡新能源出力波动,能够长期存储电能的储能系统(Energy Storage System,ESS)起到了平抑可再生能源波动的作用.因此,计及储能系统的微电网经济调度成为国内外学者研究的热点.文献[14]对并网型光储微电网储能容量优化配置进行研究分析,建立了能量管理策略.文献[15]对孤岛型微电网经济模型,考虑储能损耗,对微电网的经济性进行了调度分析.这些研究中,对于储能设备,仅仅是作为能量交换的中介,对于储能系统自身的属性分析没有过多的深入研究.
本文在已有研究的基础上,对含风机、光伏、微型燃气轮机、蓄电池组成的微电网为研究对象,提出了并网运行模式下的微电网经济调度模型.模型中在综合考虑分时电价、蓄电池综合损耗、和可转移负荷的基础上,以运行成本最小和系统负荷与目标负荷最小为多目标的微电网优化调度.采用遗传算法进行算例仿真,验证了所提模型的经济性.
1 微电网的系统构成与需求侧管理模型
1.1 微电网的基本结构
典型的微电网结构如图1所示,该微电网系统主要是由光伏发电机(Photo Voltaic Cell,PV)、风力发电机(Wind Turbine,WT)等清洁能源发电单元、微型燃气轮机(Micro Turbine,MT)以及储能系统(Energy Storage System,ESS)组成微电网的发电系统与固定负荷(Fixed Load,FL)、可转移负荷(Transferable Load,TL)、能量管理系统(Energy Management System,EMS)等组件构成.分布式电源通过电气控制系统(Electrical Control System,ECS)、DC/AC逆变器并联在交流母线上,微网各个分布式单元通过系统控制器与微电网控制中心联接起来形成通信网络.整个系统能够基于EMS通过通讯信道实现分布式能源网络能量管理集成以及发电单元的有效控制,是微电网优化运行控制的关键.
1.2 需求侧管理模型
对需求侧负荷进行分类,有助于能量管理以及制定合理的调度计划.本文主要将微电网用电负荷按供电可靠大小分为固定负荷和可转移负荷.固定负荷即为重要负荷.重要负荷一般在日常生活中由重要作用的负荷,若对其断电会引起政治、经济方面的重大影响.因此,在系统正常运行时必须对其保持持续可靠的供电,不可对其进行平移和中断.可转移负荷是指在供电方式上具有一定的灵活性的负荷,这种负荷的可控性很强,负荷的供电时间可按计划变动,如洗衣机、洗碗机、空调等.电力部门对可转移负荷的容量进行估计,与用户签订合约,增加微网的经济性.其数学模型为
(1)
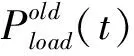
可转移负荷有不同的用电持续时间,既有用电持续时长为一个Δt的可转移负荷,也有用电持续时长为大于一个Δt的可转移负荷.因此P(t′,t)和P(t,t′)的数学模型为[16]
(2)
(3)
公式中:nL1为可转移负荷的种类总数;nL2为运行时间大于一个调度时段的可转移负荷种类数;Lmax为可转移负荷的最大运行时间;Ak(t′1,t)、Ak(t′1,t-l)分别为第k类可转移负荷从t′1时段转移到t时段、t-l时段的负荷单元数量;Bk(t,t′2)、Bk(t-l,t′2)分别为第k类可转移负荷转出的单元数;P1.k为第k类可转移负荷单元在第一个运行时段的功率;P(l+1).k为第k类可转移负荷单元在第l+1个运行时段的功率.
当用户侧参与需求管理时,电力部门应对用户进行经济补偿.现有的研究只考虑到转移负荷量的大小对用户用电的影响,忽略了可转移负荷调整时间间隔对用户用电舒适度的影响[15-18],调整时间间隔越大,对用户的用电习惯影响就越大,造成用户用电的不舒适度就越高,本文对综合考虑转移的负荷量大小补偿成本和不舒适度补偿成本.具体数学模型为
(4)
公式中:ρ为可转移负荷单位功率的补偿费用;∂为单位功率不舒适度折损成本;CL转移负荷补偿成本.
2 微电网优化调度模型
2.1 各微源的成本模型
2.1.1 可再生能源运维成本
(5)
公式中:Ci,om为第i个可再生能源运维成本;Ki,om第i个可再生能源单位功率运维成本系数;Pi(t)为第i个可再生能源t时段实际出力.
2.1.2 微型燃气轮机模型
微型燃气轮成本模型为
(6)
(7)
(8)
由于微燃机在发电的过程中,需要消耗天然气,会产生CO2、NO2、SO2等大气污染物.所以,需考虑环境成本,环境成本包括两种:(1)排放污染物需要缴纳的罚款,如表1所示;(2)对环境价值的损失,即将环境看做一种资源,对环境污染相当于对环境资源的消耗,包括由于直接排放污染物环境质量的下降和过度消耗自然资源对生态环境造成破坏[17],如表1所示.因此,微燃机环境成本可表示为
(9)
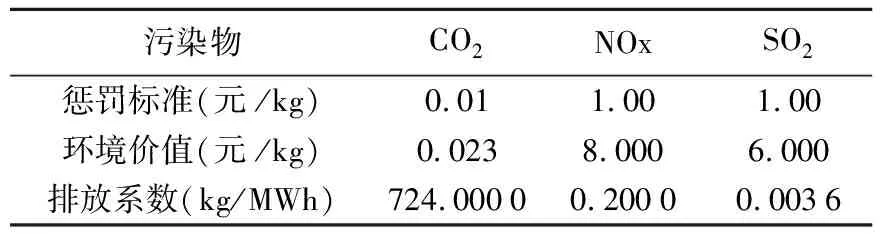
表1 污染物罚款标准、环境价值标准和排放系数
公式中:m为污染物的种类;Vhj为微燃机发出单位功率时第j项污染物环境价值损失的惩罚成本;Vj为单位功率第j项污染物排放所受的罚款成本;Qj为单位功率下第j项污染物的排放量,如表1所示.
综上所述,微燃机综合成本为
(10)
2.2.4 储能系统模型
(1)蓄电池充放电模型
(11)
公式中:SOC(t)为t时段储能系统的荷电状态;Pc(t)、Pd(t)分别为t时段储能系统充、放电功率;ηD、ηC分别为储能系统充、放电效率.
(2) 蓄电池寿命损耗成本模型
铅酸蓄电池的工作寿命与温度、峰值电流、充放电循环和放电深度(Depth of Discharge,DOD)等因素的影响.其中DOD的大小是影响电池使用寿命的最关键因素,DOD越大,蓄电池的最大循环次数就越少,蓄电池的工作寿命就越短.铅酸蓄电池不同的DOD下最大循环次数一般由电池厂家通过测试给出.由于实际运行中,蓄电池在每个调度时段实时变化的.可采用等效循环寿命法对调度周期内蓄电池的寿命损耗进行测算.
等效循环寿命法是将蓄电池不同DOD所对应的最大循环次数N(DOD)折算全充全放时即DOD=1时的等效循环次数N(DOD=1)并累加和,再根据DOD=1时的最大循环次数N(DOD=1)计算蓄电池的实际工作寿命.蓄电池在调度周期充放电循环一般用SOC的变化曲线来表示.一个完整的循环周期是由一个放电半周期加上一个充电半周期构成,第k次充放电循环的一个充电半周期为SOCa→SOCb,一个放电半周期为SOCb→SOCa,则SOCa→SOCb→SOCa为第k次充放电循环的一个完整的充放电周期,其中0≤SOCa≠SOCb≤1.则对应的DODk为
DODk=|SOCb-SOCa|,
(12)
则蓄电池的等效循环系数α为
(13)
公式中:N(DODk)为第k次循环放电深度DODk对应的最大循环次数;N(1)为DOD=1时的最大循环次数;α(DODk)为第k次循环放电深度为DODk下循环一次等效为DOD=1下的循环次数,其中0≤α(DODk)≤1.
根据蓄电池实际工作中一个调度周期的SOC变化曲线,可以通过雨流计数法来进行统计和提取[18-19],一个调度周期内,蓄电池充放电总循环周期数为n,对应DOD1,DOD2,DOD3,…,DODn,则该调度周期内,蓄电池的等效循环次数为
(14)
所以一个调度周期内蓄电池寿命损耗成本为
(15)
公式中:Ccost为储能投资安装成本.
整体计算步骤流程,如图2所示.
蓄电池循环寿命与DOD关系曲线参照文献[20],如式(16)所示.
N=-3 278DOD4-5DOD3+12 823DOD2-14 122DOD+5 112
.
(16)
蓄电池在实际工作中,其使用寿命还会受到蓄电池的荷电状态值的影响.蓄电池在其荷电状态过高过低的情况下充放电都会对蓄电池使用寿命造成影响.所以,设置蓄电池荷电状态警告区域,如图3所示.当蓄电池荷电状态位于警告区域时,产生惩罚费用,使蓄电池尽快进入安全区域工作.惩罚费用为
(17)
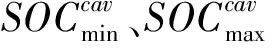
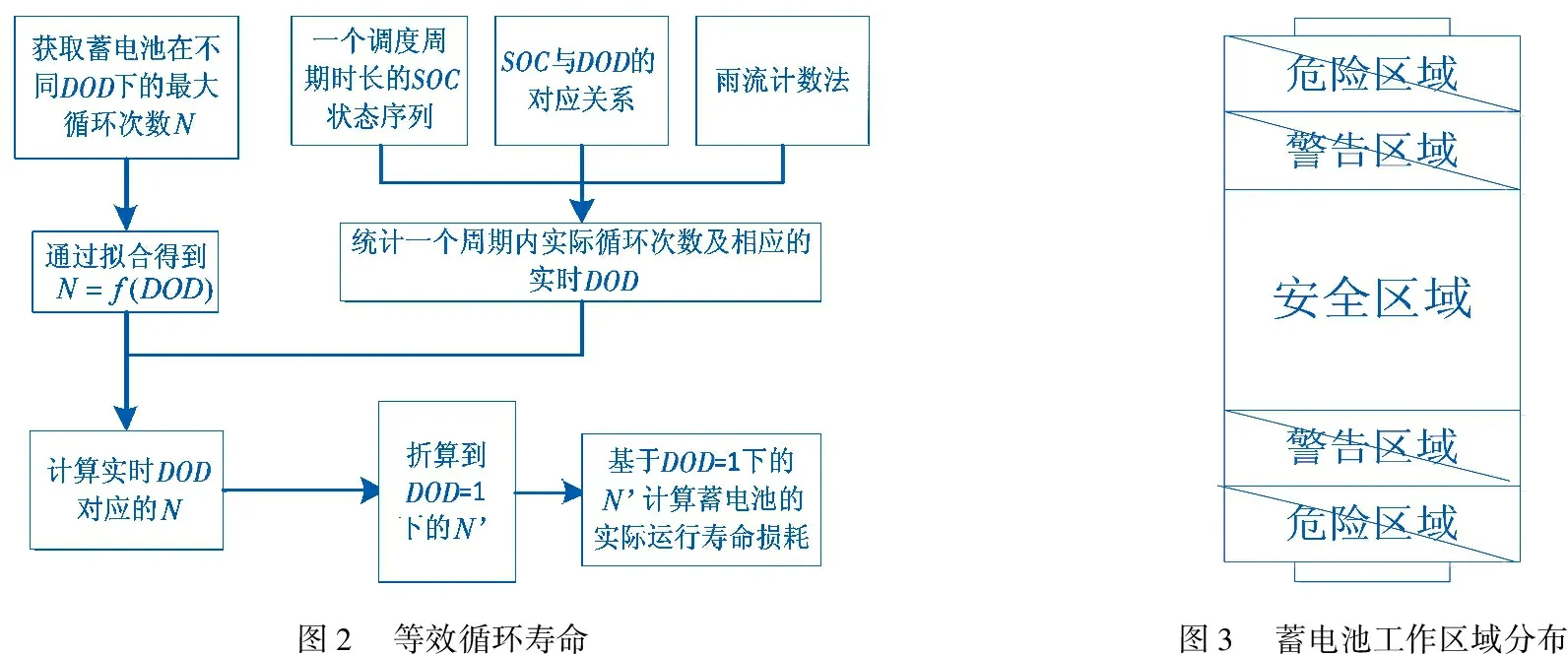
图2 等效循环寿命图3 蓄电池工作区域分布
综上所述,所有的储能系统的损耗成本为
CSB(t)=Closs+Cw(t)
.
(18)
2.2 目标函数
目标1:本文采用日前调度模型,以一天内微网分布式电源以及蓄电池的运维成本、微燃机综合成本、微电网向主网购电成本和向微网售电利润、以及可转移负荷补偿费用之和最小为优化目标.因此微电网一天内的成本函数可表示为
minF1=Ci,om+CMT+CSB+Cbuy-Csell+CL,
(19)
(20)
(21)
公式中:Cbuy(t)、Csell(t)分别为t时段微电网向主网的购电费用和售电收益;eb(t)、es(t)为t时段向主网实时购电、售电电价;Pgrid(t)为微电网与主网之间的交互功率,当微电网向主网购电时为正,向主网售电时为负.
目标2:用户侧参与考虑需求侧响应后,调度后的负荷曲线和新能源发电曲线时序上最大化贴近,尽可能实现分布式能源就地消纳最大化、自发自用.所以,以系统净负荷最小为目标,目标函数可表示为
(22)
则最终目标函数形式为
minF=ω1F1+ω2F2,
(23)
公式中:ω1和ω1为权重系数,本文考虑到用户的舒适度,ω1不宜过大,ω1取0.2,ω2取0.8.
2.3 约束条件
2.3.1 功率平衡约束
假设系统内部无网络损耗,系统功率平衡约束为
PWT(t)+PPV(t)+PSB(t)+PMT(t)+Pgrid(t)=Pload(t)
.
(24)
2.3.2 微源出力约束
(25)
2.3.3 储能系统运行约束
(1)SOC状态约束
SOCmin≤SOC(t)≤SOCmax,
(26)
公式中:SOCmin、SOCmax分别为蓄电池组的SOC状态下限和上限.
(2)充放电功率约束
(27)
(3)充放电互斥约束
(28)
公式中:SOC(t)为储能系统在t时段的荷电状态;μt、πt为状态变量,分别表示储能系统的充、放电状态.
(4)周期储能平衡约束
对于储能系统,在经过一个调度周期T后,储能系统的存储能量需要回到调度前储存能量的初始值表达式为
SOC(1)=SOC(T)
.
(29)
2.3.4 爬坡率约束
(1)微燃机爬坡功率
0≤PMT(t+1)-PMT(t)≤dPMT,
(30)
公式中:dPMT为微燃机爬坡速率约束值.
(2)与大电网交互功率约束
Pgrid,min≤Pgrid(t)≤Pgrid,max,
(31)
公式中:Pgrid,min、Pgrid,max为微电网与主网交互功率的上下限.
2.3.5 可转移负荷约束
(1)可转移负荷时间区间约束
(32)
公式中:fk.t为可转移负荷的可转入最早时间段;dk.t为可转移负荷的转移时间段区间;Ak.t.t′为第k类可转移负荷从t时段转移到t′时段的负荷数量.
(2)可转移负荷数量约束
(33)
公式中:Pinmax为最大负荷转入量、Ptrload(t)为t时段可转移负荷容量.
3 并网微电网能量管理与可转移负荷调度策略
3.1 微电网能量管理策略
本文考虑到主网分时电价机制,即将全天24 h划分为峰、平、谷三种时段,把3种时段作为三种前提来控制可控性微源的出力、蓄电池充放电功率以及微电网与主网之间的交互功率.引入净负荷概念,其数学表达式为
ΔPnet(t)=Pload-PWT-PPV
.
(34)
并网运行控制策略如图4所示.其中优化策略A、优化策略B、优化策略C分别对应谷时段、平时段、峰时段的优化控制策略.
(1)谷时段调度策略
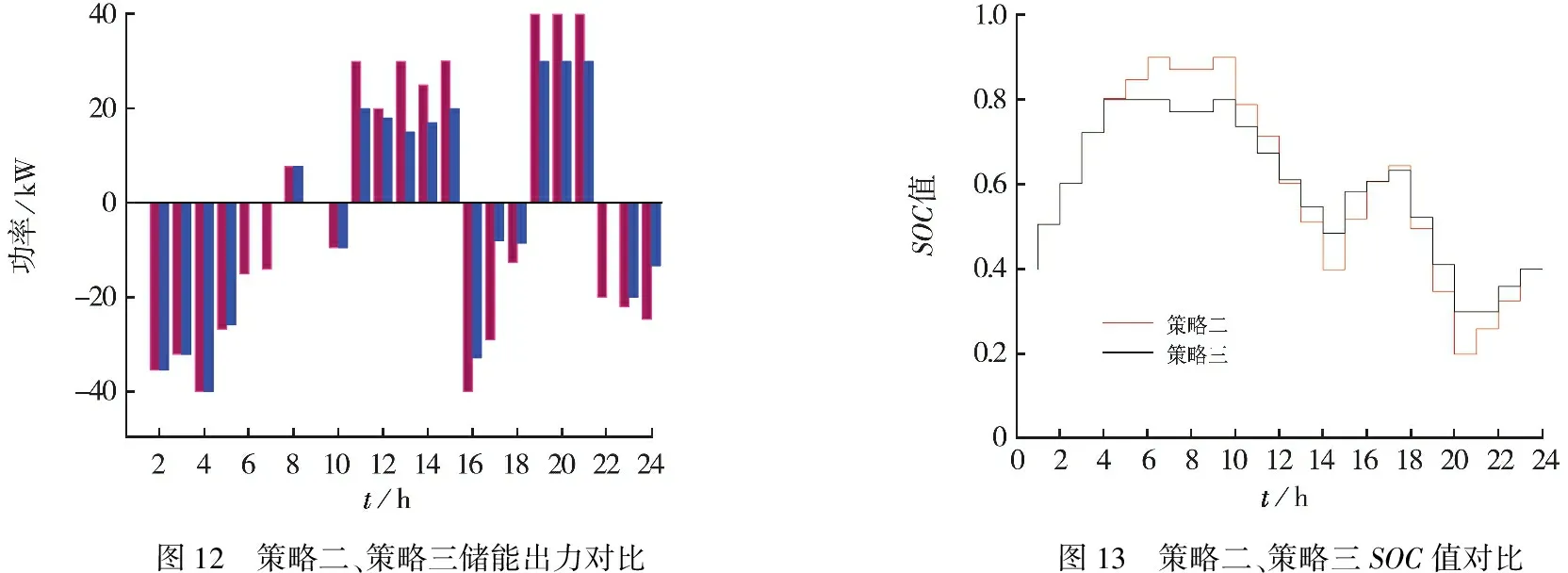
当ΔPnet(t)<0时,若SOC(t) (2)平时段调度策略 当ΔPnet(t)<0时,若SOC(t) (3)峰时段调度策略 当ΔPnet(t)<0,由于峰时段售电电价较高,所以应尽量售电.若|ΔPnet(t)| 本文提出一种可转移负荷调度策略,综合考虑主网的分时电价、新能源消纳以及净负荷与储能放电功率的关系,先确定可转移负荷在各个时段是否转入、转出或不转移,再确定各可转移时段转移负荷的种类和单元数.这样可以有效减少待求变量的维度,提高计算精度和速度,减少计算量.具体的调度策略步骤如下: (1)预测基本数据信息.预测一天24个时段每个时段的风电功率,光伏功率和负荷平均功率,收集用户侧设置的可转移负荷种类和单元数信息. 本文的规划为约束非线性规划,可采用内点法对目标函数进行寻优,然而所有非线性寻优算法均存在易陷入局部极值的问题.因此,本文利用遗传算法优化内点法初值,尽可能的避免算法陷入局部极值,具体步骤如图6所示. 本文以一个含风力发电机,光伏发电系统、微型燃气轮机和蓄电池的微电网为例,多种微源的微电网系统为例.微电网的可控微源基本信息,如表2所示.蓄电池采用铅酸蓄电池,额定容量为300 kWh,基本参数如表3所示.联络线传输功率上限100 kW,最大返送功率不超过100 kW.为日前风力发电机预测出力、日前光伏发电预测出力、日前负荷预测结果,如图7所示.可转移负荷参数,如图8所示.采用分时电价,电价如表4所示. 表2 可控微源基本参数 表3 蓄电池基本参数 表4 分时电价 设定两类可转移负荷,工作时间分别为1 h和2 h,两类负荷的功率曲线如图8所示.ρ取0.05,∂取0.02. 为了验证方案的有效性和可行性,本文设立了三种策略对比方案;策略一:不考虑需求侧响应,不考虑储能综合损耗;策略二:仅考虑储能综合损耗;策略三,综合考虑需求侧响应和储能综合损耗.其中策略一的调度结果,如图9所示. 从图9中可以看出,风力出力、光伏出力与预测出力曲线一致,说明低成本的风机和光伏优先发电.微燃机在0:00~10:00处于停运状态,在峰时段满发运行,说明微燃机发电成本高于平时段和谷时段的购电电价,低于峰时段的购电电价.在10:00~15:00第一个峰时段中,由于系统净负荷较低,微燃机满发,蓄电池增加出力,在满足系统内部负荷的情况下,向电网售电获取利润.18:00~21:00,由于风光出力较低,负荷较高,此时微燃机,蓄电池满发出力,并向大电网购电来维持对负荷的供电.策略二的调度结果,如图10所示. 图9 策略一调度结果图10 策略二调度结果 在策略二中,由于可转移负荷参与调度,12:00~13:00,、14:00~15:00、16:00~21:00时间段的负荷明显减少.23:00~01:00、05:00~08:00时间段的负荷有明显的提高.负荷从峰时段转移到的谷时段和新能源充足的部分平时段,达到了削峰填谷的目的.由于考虑到用户舒适度,01:00~05:00没有转入负荷,并且峰时段的负荷大多平移到了时间间隔较短的谷时段.对比图9、图10,通过负荷转移,12:00~13:00、14:00~15:00时间段微网向主网售电功率有所提升,增加了售电利润.并且18:00~21:00时间段,向主网购电功率明显降低,减少了购电成本,提高了微网的经济性. 在策略三中,考虑储能损耗和储能荷电状态管理后,得到了更加精准的蓄电池模型,为微电网优化调度运行提供了更精确的依据.策略二与策略三储能出力情况和蓄电池SOC状态,如图12、图13所示. 图12 策略二、策略三储能出力对比图13 策略二、策略三SOC值对比 从图12可以看出,在考虑了储能综合损耗后,在10:00-15:00之间,储能的放电深度明显降低,储能在此时段对主网进行削峰填谷获取售电利润的同时,受自身综合损耗成本的约束减少储能自身损耗,从而延长储能使用寿命.在18:00-21:00之间,储能放电深度亦有所降低,这是因为储能以较高的放电深度出力所产生的储能综合损耗成本高于此时段向主网购电成本.由图13可以看出,策略三的SOC值的更加平稳,蓄电池的剩余能量保持在安全区域内,整体放电循环深度有明显的降低. 表4 各策略成本 各策略成本,如表4所示.比较策略一、策略二,通过负荷转移,微网运行总成本有所降低,向主网购电费用减少约30.9%,提高了微网的经济性.策略三中,微网的运行成本有所升高,是因为考虑了储能综合损耗,模型更加全面精确,成本提升了约10%,这也说明了在微网经济调度过程中,储能综合损耗问题不可忽视. 本文建立了考虑需求侧管理的微电网优化调度模型,模型中综合考虑系统运维成本、蓄电池综合损耗成本、与主网交互成本以及可转移负荷补偿成本.针对可转移负荷的求解问题,提出了一种综合考虑系统净负荷和分时电价的负荷调度策略,有效的降低了负荷求解难度.针对蓄电池损耗问题,综合考虑了蓄电池寿命损耗和SOC状态管理,使蓄电池在安全区域下运行.通过算例的计算与分析,验证了本文所提出的模型的精确性和有效性.3.2 可转移负荷调度策略

4 模型求解算法
5 算例分析
5.1 模型参数



5.2 结果分析


4 结 论
