陡脉冲干扰下的心电信号滤波及QRS提取
2020-06-05姚晰童张建勋葛锦涛
姚晰童,代 煜✉,张建勋,葛锦涛,陈 通,杨 灏
1) 南开大学机器人与信息自动化研究所,天津 300310 2) 南开大学电子信息与光学工程学院,天津 300310
陡脉冲是指短时高压电脉冲.通过向细胞施加陡脉冲可以使得细胞出现瞬时的电穿孔.基于这种特性,陡脉冲广泛的应用于靶向药物传递[1]、癌症治疗[2]等多个领域,其可行性已经在人体实验中得到了证实[3].除此之外,陡脉冲在材料领域[4]、食品工业[5]也有着广泛的应用.
心电是心脏活动的重要表现,是医生对患者生理状态进行判断的重要佐证.然而,心电信号(Electrocardiogram, ECG)受到陡脉冲的干扰,波形可能发生变异,这导致病患的生理状况无法被掌握,影响治疗效果.以不可逆电消融疗法[6]为例,心电信号的作用除监测患者生理状态外,还包括同步陡脉冲的施放,如果不将陡脉冲的施放时间与心电周期同步,手术范围将被严格的限制在远离心脏的20 cm的范围外.
目前,对心电信号的滤波算法的研究,主要针对高频噪声、基线漂移、工频干扰,对于陡脉冲干扰的滤波算法研究较为缺乏.由于陡脉冲产生的相关噪声与心电信号主成分频带重合,经典的数字滤波器[7]虽然简单易实现,但是效果较差;小波算法[8]对心电信号滤波是基于信号与噪声频谱分离特性,运用于此场景效果不理想,且小波基的选择影响最终结果;基于EMD的滤波算法[9]改进了小波算法的缺陷,但是对分解信号的进一步处理需要依赖经验,且对采样频率和噪声敏感.因此,本文针对陡脉冲干扰的特性,基于VMD[10]算法提出了解决方案,实现了对陡脉冲干扰下心电信号的滤波并满足了心电周期同步需求.
1 陡脉冲干扰下心电信号的分析
陡脉冲具有如下特征:脉冲幅值要求达到kV·cm-1,脉冲上升沿时间为ns级别,脉冲宽度为μs级别[11].可用表达式(1)表示:
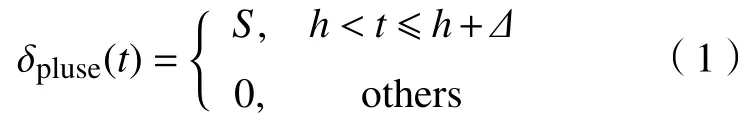
式中,δpluse(t)表示高压陡脉冲的时域曲线,S为陡脉冲幅值,Δ为陡脉冲脉宽,h为陡脉冲施放时间点.陡脉冲对ECG的干扰如图1所示.时域上可将陡脉冲干扰分为两个部分,即:前支和后支.其中,前支频率高,时间短,位于心电信号中的不应期,相当于陡脉冲对心电采集设备等效RC电路的充电过程;后支以前支的终点为起点,频率低,时间长,对心电信号的波形影响较大,其数学模型如式(2):
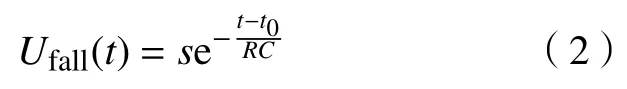
式中,Ufall为陡脉冲冲激下降沿的幅值,s为陡脉冲冲激的峰值电压,R、C分别表示人体等效电阻和等效电容,t0为陡脉冲冲激后支起点时间.此外,在医疗环境中,随机噪声伴随陡脉冲干扰心电信号.随机噪声的能量均匀的分布在整个频带上,在此以nw表示.经过以上分析可知,受陡脉冲相关噪声干扰的心电信号的数学模型如式(3):
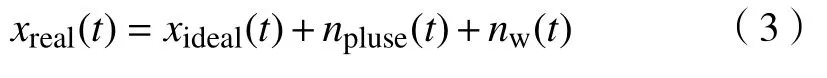
其中,xreal与xideal分别表示实际心电信号和理想心电信号,npluse表示陡脉冲干扰.
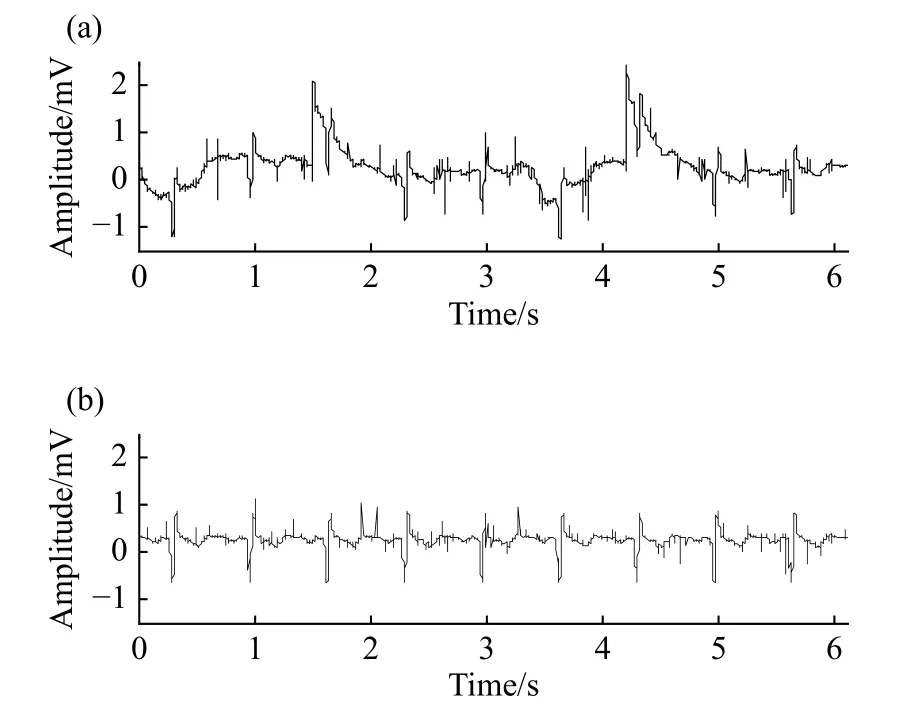
图1 受陡脉冲干扰的ECG.(a)受到陡脉冲干扰的心电信号;(b)未受陡脉冲干扰的心电信号Fig.1 ECG disturbed by steep pulses: (a) ECG disturbed by steep pulses; (b) ECG not disturbed by steep pulses
2 基于VMD的陡脉冲干扰抑制
VMD算法最早由Dragomiretskiy等于2014年提出[10],可以将任意信号x(t)分解成离散数量K的子信号uk(Band-limited intrinsic mode functions, BLIMF).每一个子信号的能量都集中在相应的中心频率wk周围,具有特殊的稀疏特性[10].其基本表达式如式(4).这是一种后验的、非递归算法,并具有带通滤波器属性[12].目前,这种算法被广泛的应用在轴承故障检测[13],地震信号分析[14],经济走势预测[15]等领域.
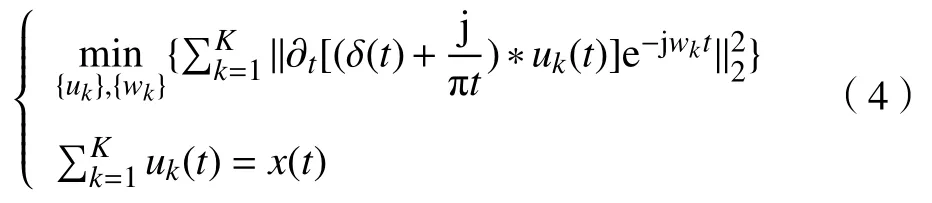
式中,K表示分割层数,uk表示第k个子信号,wk表示uk的中心频率,x表示原信号,δ(t)为狄拉克函数,∂t代表梯度运算,*代表卷积运算,j为虚数符号.
2.1 心电信号的预处理
根据香农采样定律,信号的频带宽度是采样频率的0.5倍.以500 Hz的采样频率为例,实际信号的宽度为0~250 Hz.而心电信号的主要成分集中于0.05~49 Hz[16].因此,不对50~250 Hz的信号进行分析,以提高实时性.在此,采用了一个4阶IIR滤波器对这部分信号进行衰减,截止频率为50 Hz.
2.2 陡脉冲干扰的抑制
对式(2)进行傅里叶变换,可得其幅频曲线A(f),如式(5).
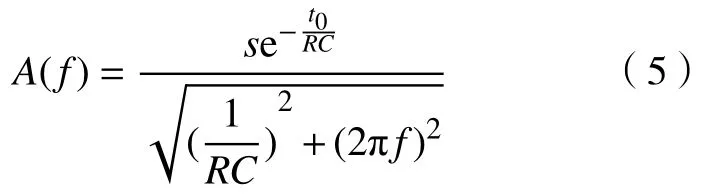
式中,f表示频率.由于心电采样设备通常要求大输入电阻[17],因此1/RC为常数且较小,在此为方便分析将其忽略.幅频特性如图2.
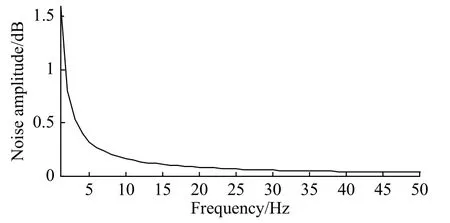
图2 衰减模型单边幅频图Fig.2 Diagram of a single-sided amplitude-frequency attenuationmodel
可以看到,陡脉冲干扰的后支能量主要分布在10 Hz前.VMD算法基于对混合信号的主成分估计,结合其带通滤波器属性,包含陡脉冲干扰后支的子信号对应中心频率wk应小于10 Hz.由于此部分干扰对心电波形干扰较大,是抑制的重点.图3展示了当K=6时,各子信号时域图.其中,子信号u1的中心频率w1接近于0,包含直流分量、基线漂移、陡脉冲干扰的低频干扰分量.将u1抛弃,可以有效地消除基线漂移和直流分量.u2的中心频率满足w2<10 Hz,包含陡脉冲干扰分量、P波、T波分量[16].完全抛弃u2不利于恢复心电信号.
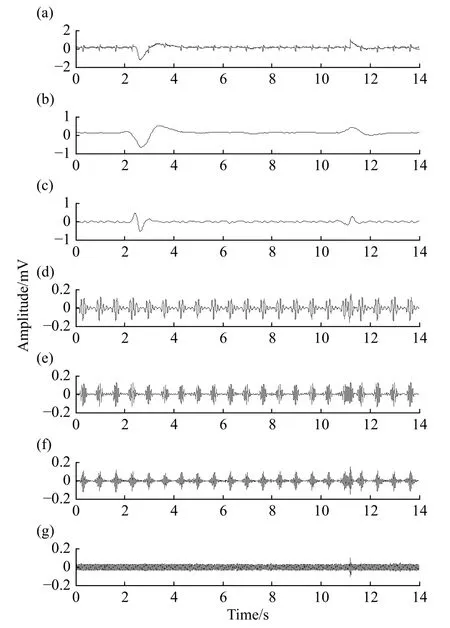
图3 VMD 6阶分解子信号.(a)原信号;(b)u1;(c)u2;(d)u3;(e)u4;(f)u5;(g)u6Fig.3 Use of VMD to divide the signal into six layers: (a) original signal; (b) u1; (c) u2; (d) u3; (e) u4; (f) u5; (g) u6
设心电采集系统共模抑制比为-100 dB,陡脉冲的峰值大于1000 V,理论上产生噪声的幅值约大于10 mV.实际测得幅值由于损耗而略小.以肢体导联为例,P波幅值不超过0.25 mV,T波幅值不超过0.5 mV[16],远低于同频段陡脉冲干扰幅值.基于以上分析,本文设计了一种自适应阈值,对陡脉冲干扰在u2中的陡脉冲干扰分量进行消除.阈值λsp如式(6).
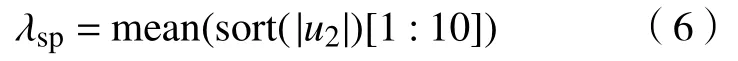
上式表示对子信号u2中绝对幅值最大的10个采样点sort(|u2|)[1:10]取 均值.sort(||)表示对输入信号序列的绝对值降序排列,mean(·)表示均值运算.
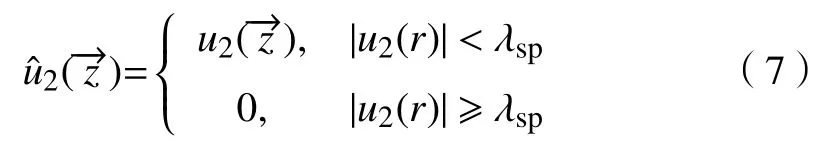
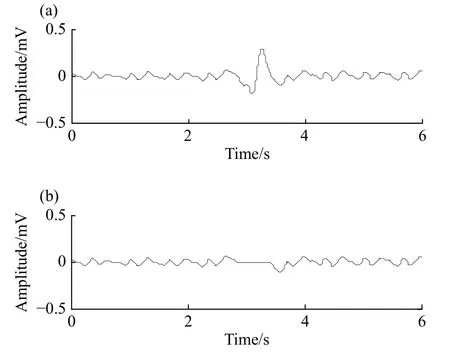
图4 u2中干扰分量消除效果.(a) 阈值处理前;(b) 阈值处理后Fig.4 Interference component elimination effect in u2: (a) before using thresholds; (b) after using thresholds
对于陡脉冲干扰前支,由于其在时域上与后支存在紧密关联,在u2之后的子信号中,以[zon-Δt,zon+Δt]为范围,搜索极大值(由陡脉冲特性,陡脉冲干扰前支时域上表现为时长短的特点,因此,Δt取500 Hz采样频率下的5个采样点,即10 ms).将极大值所属脉冲置零以完全消除陡脉冲冲激.
2.3 消除随机噪声
随机噪声由电子器件产生,在频域分布均匀,根据VMD算法的带通滤波器组特性[12],uk中的随机噪声分量的幅值远远小于原信号随机噪声幅值.受基于wavelet的阈值滤波算法[8]启发,本文提出了一种基于VMD的阈值法去随机噪声算法.由于P、T波幅值小,采用阈值消除相应子信号中的随机噪声分量可能得不偿失.因此需uk对应的wk满足式(8):
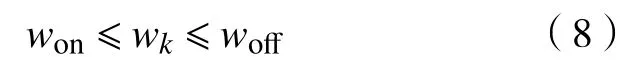
式中,won和woff分别对应P、T波频带的上限与心电信号主要频带的上限,分别取12 Hz和49 Hz[16].对满足条件的子信号uk施加阈值,如式(9).
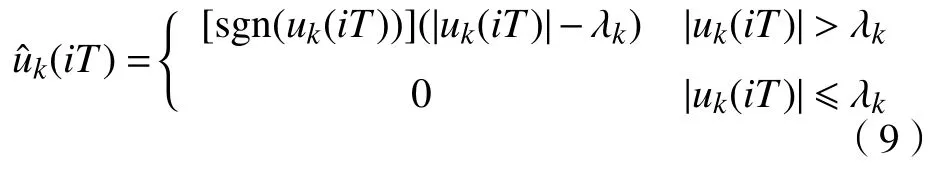
其中,i表示采样点序号,T为采样周期,sgn(·)代表阶跃函数,λk代表uk的阈值.如下式(10)所示.
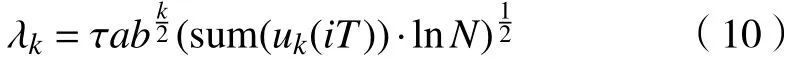
式中,N代表uk中采样点的数量,a和b均为常数[18].τ为比例因子.施加阈值后效果如图5.
最终,抑制噪声后的心电信号用xfilter表示.如式(11)所示:

图5 消除随机噪声分量之后的子信号.(a) u4;(b) u5Fig.5 Sub-signal after eliminating random noise components: (a) u4;(b) u5
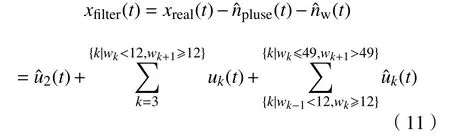
式中,w是对心电信号中随机噪声的估计,pluse是算法对陡脉冲冲激的估计.表示消除随机噪声后的uk.
3 基于VMD算法的QRS提取
在心电信号中,QRS波群的能量集中在8~16 Hz之间[16].如式(12)所示,则可以提取QRS波群主要成分.
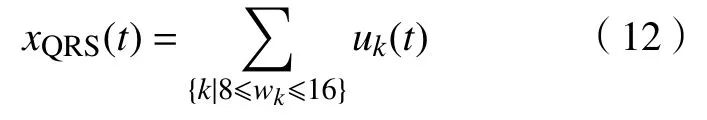
在重组信号xQRS的基础上,对QRS波群进行检测,可避免P、T波等信号对检测过程的干扰.为了突出R波的位置,对重组信号进行预处理.预处理算法如式(13)、(14)、(15)所示,依次对重组信号序列表示差分、平方、积分运算.xdiff、xsq、xmvw分别是差分、平方、积分运算的输出.式中,T表示采样周期,W表示移动滑窗宽度,在此取80 ms效果较为理想,这与R波的实际宽度有关[19].效果如图6(c)所示.
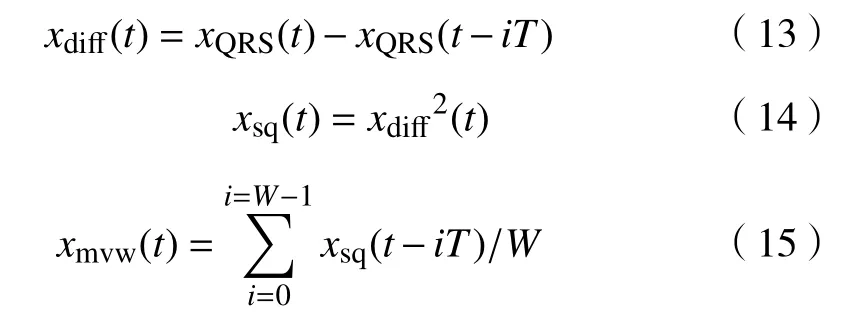
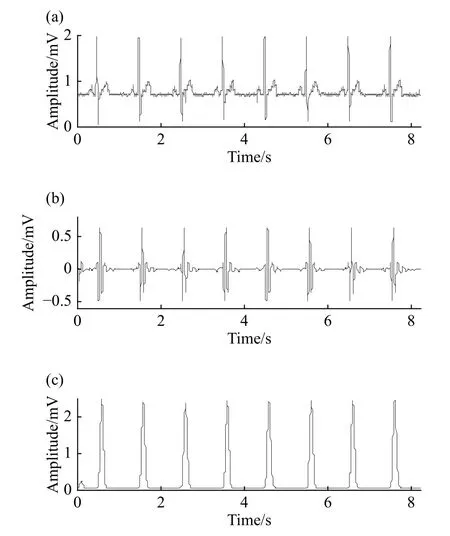
图6 R波检测的算法验证.(a) 原信号;(b) 重组的QRS;(c) R波增强Fig.6 Verification of the R-wave detection algorithm: (a) original signal; (b) restructured QRS wave; (c) enhanced R wave
处理之后的心电信号,采用阈值法对R波峰值点进行提取.初始阈值λ0由最初10个1 s内预处理后序列极大值的均值决定.随后,每检测到一个R波即对阈值进行更新.阈值更新算法如式(16).
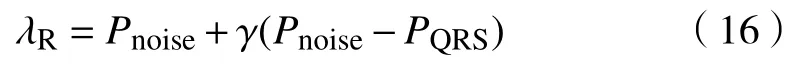
式中,λR为当前R波的检测阈值,Pnoise和PQRS分别是最近n个非R峰值点幅值的均值和最近n个R峰值点幅值的均值.γ为比例常数,当n取8时,γ取0.475效果最佳[19].算法流程图如图7.图中,rm-1和rm分别表示第m-1个和第m个已经被定位的R波所在位置,rrmean表示连续n个RR间期长度;tRP为不应期,此期间无R波,时长为200 ms[20];max[.]表示求括号中的最大值.
4 实验和数据分析
实验部分采用MIT-BIH数据库数据与实际采集的心电信号共同验证本文中提出的算法.图8(a)所示,是天津市机器人与智能重点实验室研制的不可逆电脉冲消融设备样机,可以释放峰峰值范围1000~3000 V的陡脉冲.为采集受陡脉冲相关噪声干扰的心电信号,本文采用TI公司ADS1298芯片,自行设计制作了心电信号采集设备,如图8(b)所示.本文的实验部分,陡脉冲的峰峰值为1000 V.
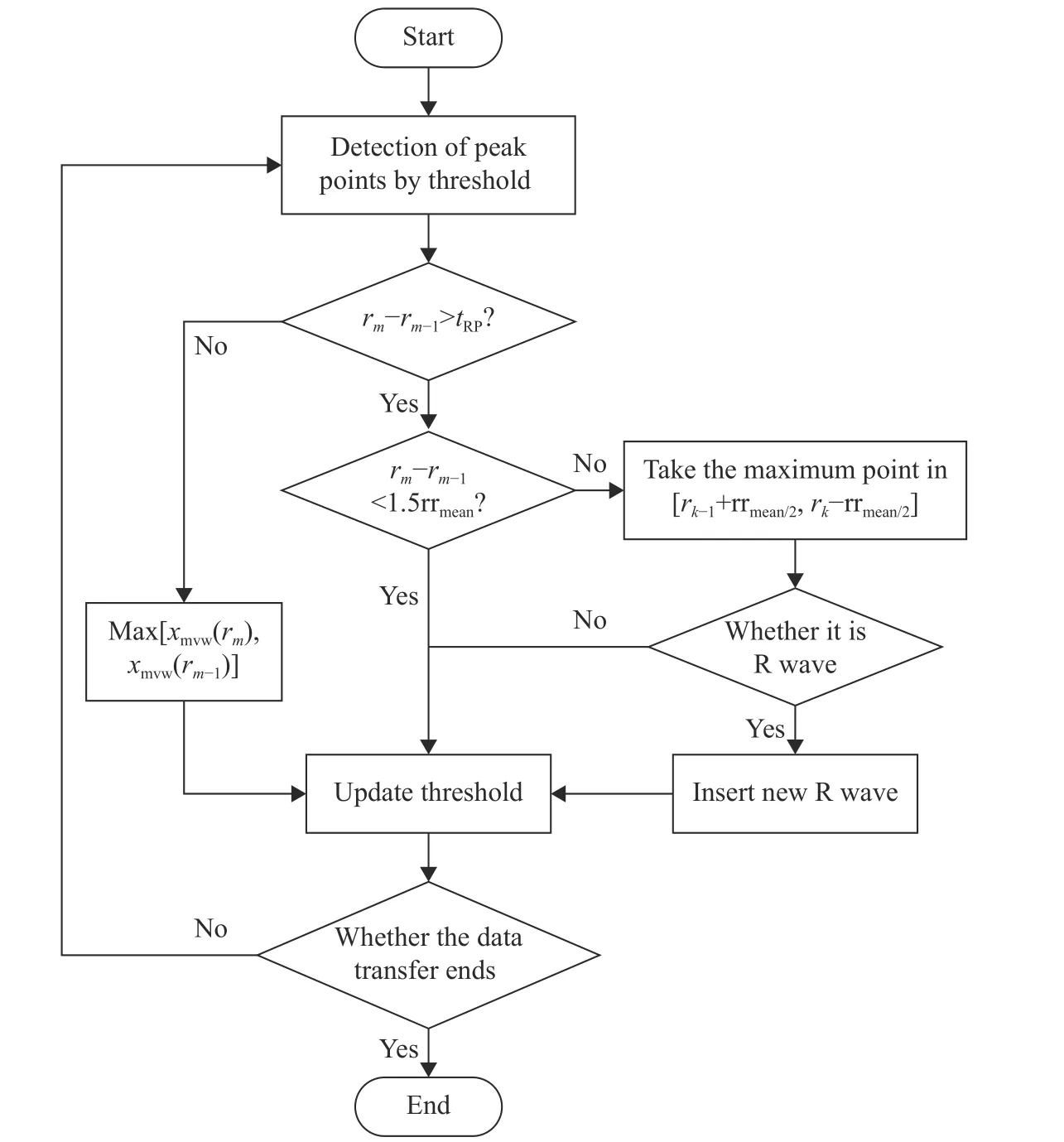
图7 R波检测的算法流程图Fig.7 Flowchart of the R-wave detection algorithm

图8 实验设备展示.(a) 不可逆电消融样机;(b) 心电信号采集板Fig.8 Experimental equipment: (a) prototype of irreversible electrical pulse ablation surgery; (b) ECG signal sampling circuit
4.1 ECG滤波算法实验
4.1.1 预处理对实时性的提升
实验平台基本参数:主频2.9 GHz,i5处理器,运行内存8 G,Windows10操作系统.本次实验选用500 Hz采样频率下16.384 s的包含陡脉冲干扰的ECG信号为实验对象.
图9对比了心电信号是否预处理对w2的影响.根据VMD相关理论,分解层数K应当尽可能的少以节约计算时间;同时u1表示基线信息因而w1约等于0,w2的值意味着分解的有效性.当w2<10 Hz时有效分离高压陡脉冲干扰.若不进行预处理,分解层数K≥14时可将陡脉冲干扰与QRS波群分离.当K=14时,耗时30.1939 s.如对ECG进行预处理,当K≥5时即满足要求.当K=5时,仅需2.511 s.显然,对带噪心电信号预处理可以有效提高实时性且并较少内存耗费.
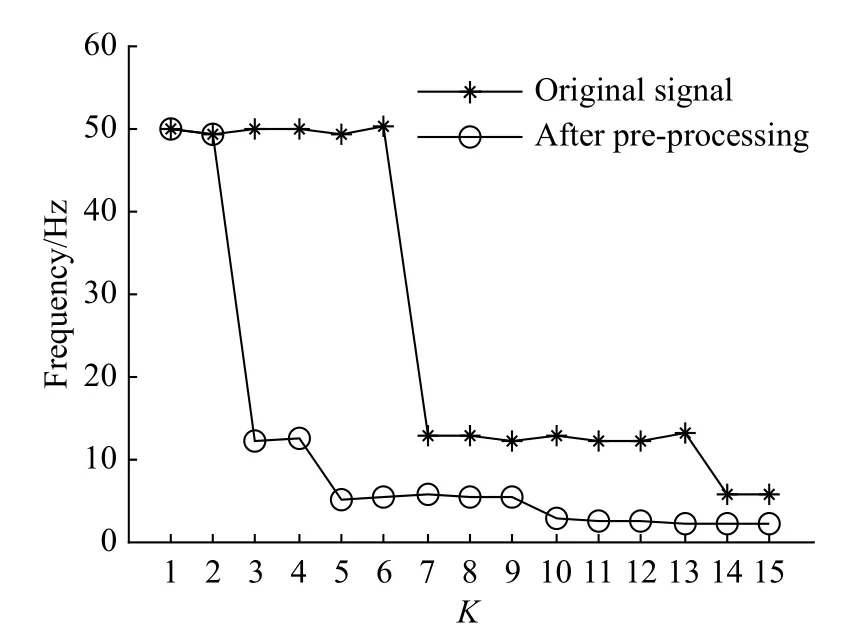
图9 信号预处理效果对比Fig.9 Effect of signal preprocessing interference
4.1.2 惩罚因子α和分解层数K的确定
惩罚因子α和分解层数K是VMD算法两个重要的参数,决定了滤波器通频带宽度[10].由图9,对心电信号进行预处理的条件下,分解层数K应满足{K|K∈[5,9]}.为进一步确定参数,设计以下实验:选取MIT-BIH数据库中第100号数据,取7200个采样点,在随机噪声级别均为5 dB的条件下,添加一定数量的模拟高压陡脉冲干扰.在此,以信噪比(Signal to noise ratio, SNR)作为评价指标,如式(17).式中,xclean表示未添加噪声的心电信号,xnoise表示添加了噪声后的心电信号,Nal表示全部参加测试的采样点数.
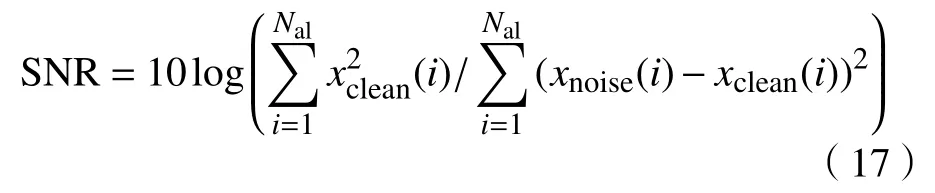
实验结果如图10所示.实验结果表明,当K=6且α=2500时,滤波效果较为理想.
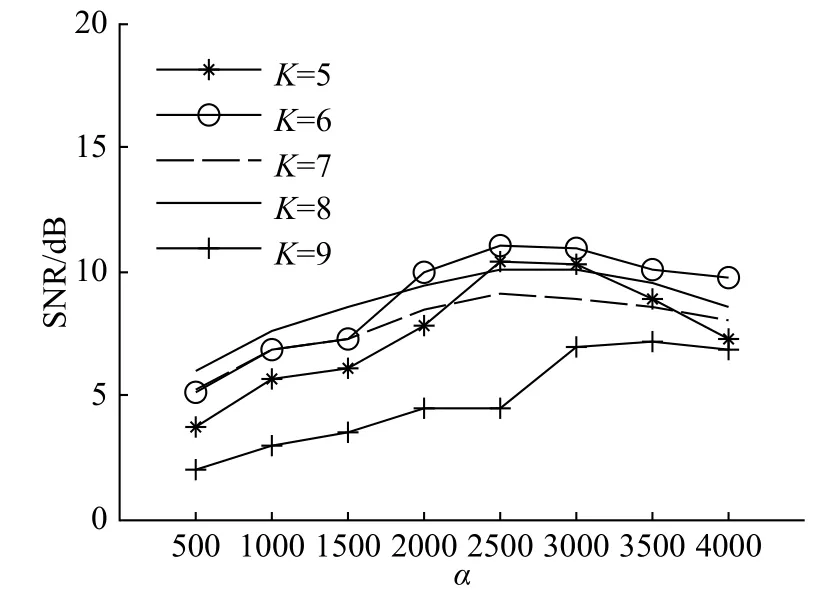
图10 对分解层数和惩罚因子进行验证Fig.10 Values of K and quadratic penalty were verified through experiments
4.1.3 陡脉冲干扰抑制
图11为对心电信号中陡脉冲干扰抑制效果.其中,图11(a)为原信号图,图11(b)和图11(c)分别是选择保留和不保留陡脉冲前支的心电信号图.可以看到,运用本算法,对陡脉冲冲激有着明显的消除效果,且最大程度上保持了心电信号应有波形.图12对比了本文提出算法与小波包阈值去燥[8]、带阻滤波算法(采用FIR带阻滤波器滤除0~10 Hz信号)在消除陡脉冲干扰时的效果.其中图12(a)为本文提出算法对陡脉冲干扰的消除效果,图12(b)为小波包阈值去燥算法对陡脉冲干扰的消除效果,虽然这种算法相对较好的保留了心电信号的特征,但是对陡脉冲干扰消除并不彻底;图12(c)为采用带阻滤波器算法对陡脉冲干扰的消除效果,此算法则完全不能保留心电信号特征,且抑噪效果差.
为进一步验证算法效果,选择MIT-BIH数据库中10段含噪声较少的心电数据,每段数据长度为16.384 s;由式(5)的数学模型,分别向心电信号中加入不同数量的模拟高压陡脉冲干扰.分别采用本文提出的算法、小波包阈值法、带阻滤波器对噪声进行处理.实验结果如表1所示.
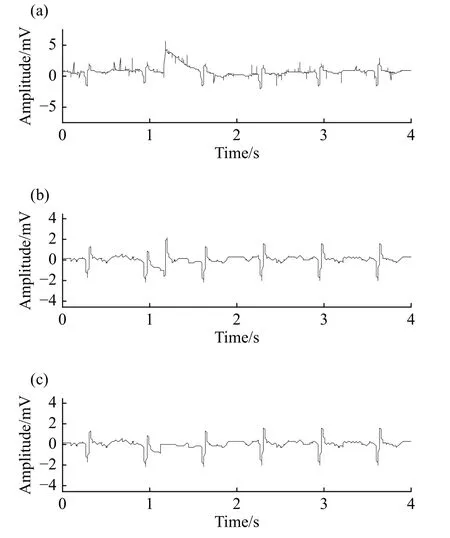
图11 施放陡脉冲期间相关噪声抑制.(a) 陡脉冲干扰消除前;(b)消除陡脉冲干扰后支;(c) 完全消除陡脉冲干扰Fig.11 Result of eliminating steep pulse interference: (a) ECG disturbed by steep pulses; (b) forehead is retained; (c) fore branches are eliminated
表中,第一列表示加入不同数量模拟陡脉冲干扰后的原始信号信噪比,其后三列分别表示采用不同滤波算法处理后的滤波效果,以信噪比表示.可以从以上实验结果中得出结论,本文设计算法可有效去除心电信号中的高压陡脉冲干扰,且相比于其他算法具有明显的优势.
4.1.4 随机噪声消除效果
阈值公式(10)由文献[18]提出,式中参数a,b分别取0.083和1.39.再此对参数正确性进行验证.采用一段来自MIT-BIH数据库第103条心电数据,加入一定数量的模拟陡脉冲干扰以及5 dB的随机噪声模拟真实环境.实验结果如图13所示:当a和b改变时,信噪比不同程度降低.由此,可以认为文献[18]中a,b的取值是无误的.
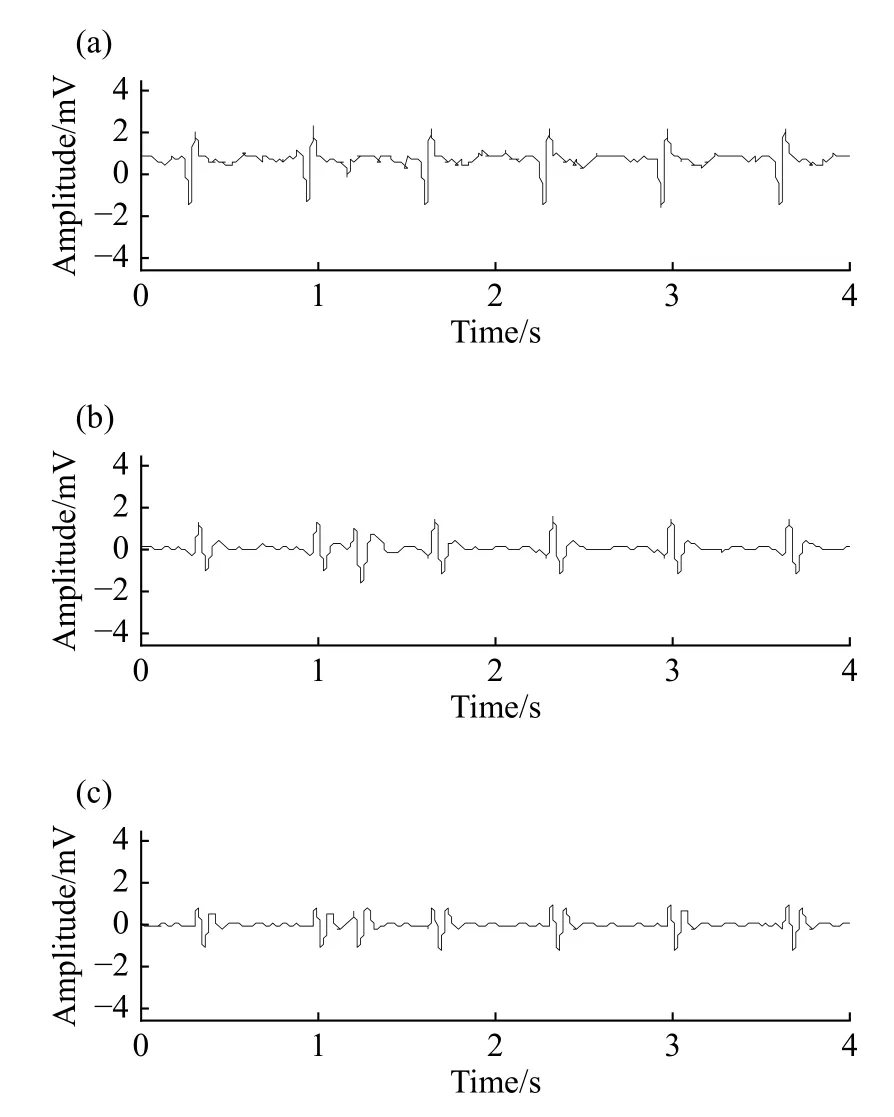
图12 陡脉冲干扰抑制效果对比.(a) 本文提出算法效果;(b) 小波算法效果;(c) 带阻滤波器算法效果Fig.12 Comparison of the results of steep pulse noise filtering: (a)algorithm in this article; (b) wavelet algorithm; (c) bandpass filter
再分别将信噪比为1~10 dB的随机噪声和相同数量的模拟陡脉冲加入到等长的心电数据中,以此数据对算法进行对比验证.表2为将本文提出的算法与wavelet去噪法[8]、EMD去燥法[9]的效果对比.信噪比越大说明信号包含随机噪声的强度越小,也就意味着对噪声的消除效果越好.
可以得出结论,在消除消融设备工作带来的随机噪声方面,本算法可以明显的提高信号的信噪比;相较于另外两种算法,提升效果更佳明显.
4.2 QRS波群检测实验和数据分析
对于R波检测准确度,采用两个指标进行评价:
(1)误检率(Error detection, ED):表达式如式(18)所示;
(2)敏感度(Sensitivity, SE):表达式如式(19)所示.

表1 陡脉冲干扰消除效果对比Table 1 Results obtained after a variety of filtering processes
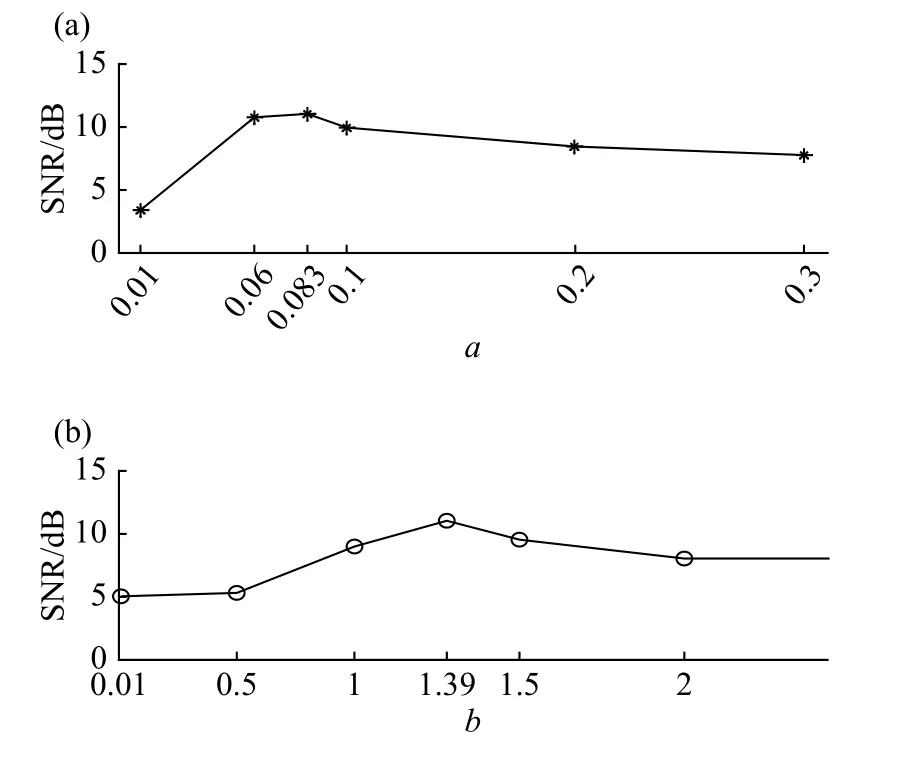
图13 a,b最优值验证.(a) b恒定a改变;(b) a恒定b改变Fig.13 Verification of the optimal values of a and b: (a) when b is constant and a is changed; (b) when a is constant and b is changed
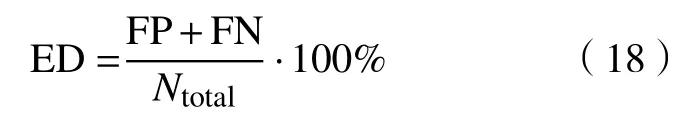

式中,TP表示正确检测,FP表示漏检的情况,FN表示误检的情况,Ntotal表示R波总数量.
为验证本算法的实际表现,采用8段来自不同患者的心电信号数据.每组数据集的时间长度均为30 min.考虑相关陡脉冲疗法的治疗位置可能位于躯干,因此,采用肢体导联作为心电信号来源,避免干扰正常治疗过程.经过人工标记,共标记16218个R峰值点.此期间,共记录释放陡脉冲522次.将本文提出算法与差分阈值法[20],带通滤波器法[21]的对比结果,实验数据如表3所示.经过对比发现,相比于本文提出的算法,其他两种算法的误检率远高于本算法,这与未对陡脉冲干扰进行抑制由直接关系.可以通过数据得出结论,本文提出的算法,在应对陡脉冲干扰下的心电信号时,有着更好的准确度和敏感度.

表2 去噪效果对比Table 2 Comparison of the results of the filtering processes
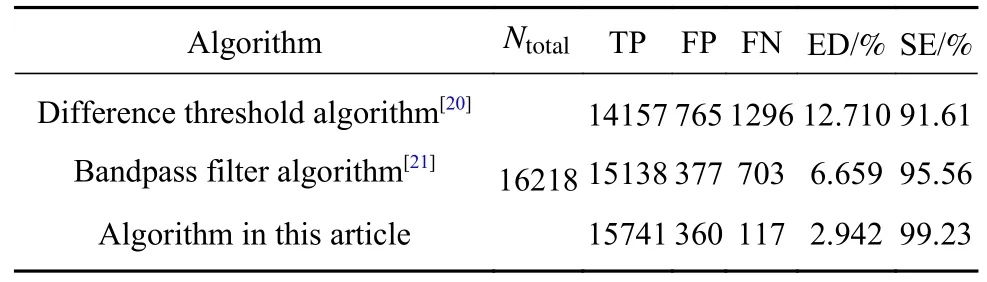
表3 与常用算法准确度对比Table 3 Comparison of the accuracy of the algorithms
5 结论
本文以陡脉冲的应用为背景,对这种特殊环境下采集的心电信号进行了研究.创新点在于:针对陡脉冲干扰特性,本文提出了一种基于VMD的心电信号陡脉冲干扰抑制算法;基于VMD特性,提出了一种阈值算法,有效的消除了电子设备带来的随机噪声;并根据分割后子信号的频域特性,提出了一种基于VMD的QRS波群提取算法.最终,以在天津市机器人与智能重点实验室研制的不可逆电消融设备干扰下采集的心电信号,与来自MIT-BIH数据库中的心电数据共同对算法性能进行了验证.结果证明,算法可以实现预期目标,且效果较为理想.其中,对陡脉冲相关噪声干扰下的ECG,提取QRS波群的准确度达到了99%以上.
