FSAE赛车差速器支撑架可靠性与轻量化协同优化设计

武彬,伍文广

(长沙理工大学 汽车与机械工程学院,湖南 长沙 410114)

FSAE赛车传动系统结构协同优化设计是一个复杂、系统的多参数和多约束优化设计问题,必须满足部件的各项结构性能。而对差速器支撑架结构进行优化设计是获得合理结构方案、提高赛车整体性能的先决条件之一。现有研究大多停留在对已完成设计的分析与验证上,且分析变量单一,很少涉及拓扑形貌等结构优化。同时,面向差速器支撑架设计的应用研究、设计方案较少,且对其优化设计不易于得到理想的参数方案,需采用新的优化策略。该文采用协同优化与可靠性分析方法,通过分析求得结构的安全系数和疲劳寿命,验证支撑架的可靠性,在满足可靠性要求的同时实现支撑架轻量化,提高赛车的安全性、动力性。

1 受力分析

赛车相关参数见表1。

表1 赛车的相关参数

图1 传动系统局部装配图

差速器支撑架受到来自支撑架和差速器的重力、支撑架中心的轴向力、耳片连接处的应力及扭矩、链传动的压轴力等载荷,其中左支撑架承受80%的链轮压轴力,而右支撑架仅承受20%,左支撑架所受载荷大于右支撑架。因此,主要对左支撑架进行受力分析。

1.1 链条传动受力计算

在链传动过程中,链条传动使大链轮处产生紧边拉力和松边拉力,即对大链轮的压轴力,经过力的传递,在差速器支撑架上产生力矩(见图2)。

不计动载荷,紧边拉力和松边拉力分别为：

F1＝Fe＋Fc＋Ff

F2＝Fc＋Ff

式中：Fe为有效圆周力,按式(1)计算；Fc为离心力引起的拉力,按式(2)计算；Ff为悬垂拉力,按式(3)计算。

式中：P为传递的功率,以最大功率计算；v为链的平均速度,v＝z1nTmaxp/(60×1 000)；z1为小链轮齿数；nTmax为最大转矩下转速；p为链条节距。

永磁同步电机矢量控制实验系统调试及故障分 析 ………………………………………… 徐 婷，戴 怡（27）

式中：q为链条单位长度的质量,为1.07 kg/m。

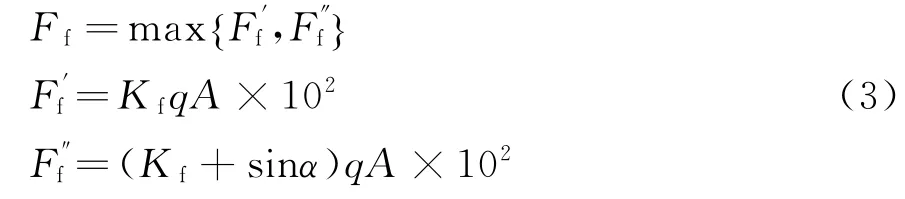
式中：Kf为垂度系数,水平传动中Kf＝6；A为链传动的中心距；α为两轮中心连线与水平面的倾斜角,水平传动中α＝1.443 1°(近似为水平)。

压轴力为：

式中：KFP为压轴力系数,水平传动中取1.12。

1.2 支撑架中心处轴向力计算

对支撑架中心处进行受力分析,支撑架垂直面上的受力和链轮的压轴力在支撑架中心处(轴承位置)产生的载荷见图3。

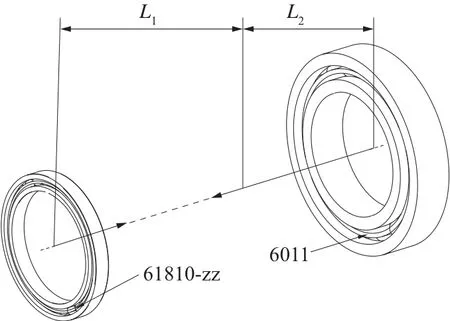
图3 轴向受力分析示意图

采用深沟球轴承,其主要承受径向载荷,也可同时承受小的轴向载荷,其当量摩擦系数最小,在高转速且有轻量化要求的场合可用来承受单向或双向轴向载荷。所选轴承的参数见表2。

在装配图中测量,得：L1＝64 mm,L2＝108.5 mm,L＝L1＋L2＝172.5 mm,FR1＝1 876.13 N,FR2＝469.03 N,按式(5)计算得轴承轴向力R1＝696.07 N,R2＝295.01 N。

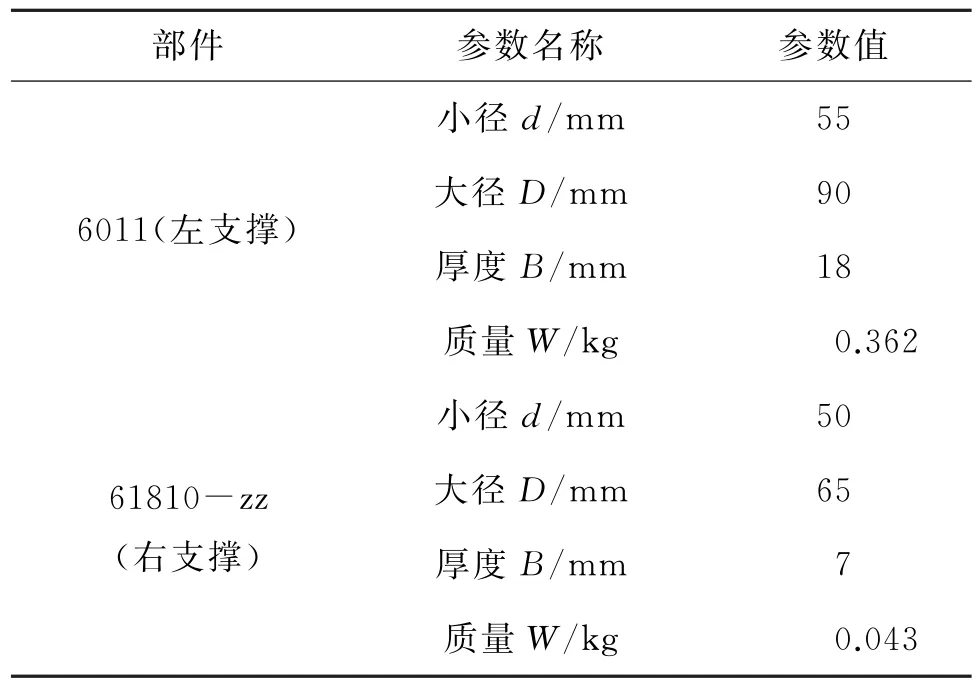
表2 深沟球轴承的参数

2 可靠性分析

2.1 模型建立与网格划分

为了满足空间布置要求,将支撑架的结构形状设计为三角形,这种结构形状能满足可靠性要求,且具有美观、易于调节的特点。图4为差速器支撑架二维图。

图4 差速器支撑架二维图

将差速器支撑架的三维模型导入有限元分析软件ANSYS Workbench的Static Structural模块,运用ANSYS Design Modeler对模型结构参数进行变量化,即多目标优化中的“定义可变参数”。定义20个模型结构参数为变量,其位置和定义见图5。

对模型进行Slice处理,将模型划分为两部分,两部分采用不同划分方案,设置不同的Body Sizing(见图6)。网格质量检查与优化贯穿于整个模型网格划分的始终。模型包含56 060个单元、89 293个节点,平均雅可比比率为1.272(＞0.7)、平均正交品质为0.818(＞0.7),网格划分质量较好。

图5 左支撑架NX模型及结构参数变量

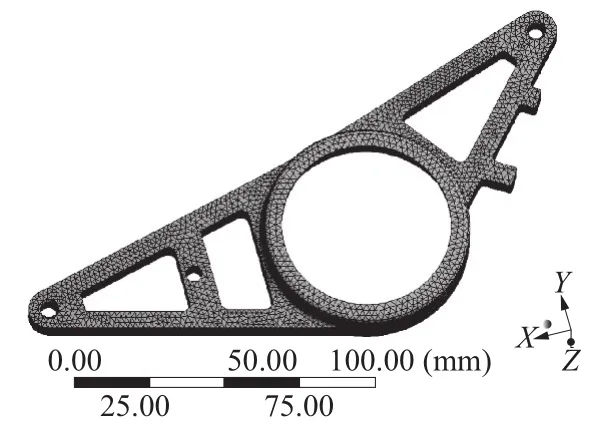
图6 差速器左支撑架Mash图

2.2 材料选择

在满足结构要求的前提下,材料应具有足够的强度且质量较轻。支撑架材料选为7075铝合金,其具有高比强度、耐锈蚀、热稳定性好、易成型、再生性好和简化结构等优点,还具有良好的机械性能和阳极反应(见表3)。

表3 7075铝合金的机械性能

2.3 模型可靠性

为模拟赛车在实际状态下承受交变载荷时的情况,采用静强度分析方法进行模型可靠性分析。先对赛车的实际工况进行分析：加速工况时,后轮的载荷最大；转向工况时,外侧轮的载荷最大。考虑转弯过程中的加速工况,计算差速器支撑架的载荷。以建立的模型为研究对象,运用CAE进行疲劳分析,预测疲劳寿命。

在差速器支撑架主体互相约束处(D)与耳片连接紧固处(C)采用固定方式。在支撑架与轴承接触面处施加所受载荷,包括压轴力、轴向力、重力等(见图7)。在网格划分与施加载荷后,通过ANSYS进行静态应力与应变分析,结果见图8、图9。

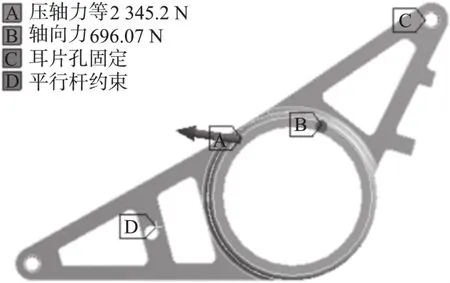
图7 差速器左支撑架载荷施加

图8 差速器支撑架的主应力(单位：MPa)

图9 差速器支撑架的主应变

应用ANSYS Mechanical进行安全系数求解,通过Safety Factor分析模块得出差速器支撑架的最小安全系数为1.94(见图10),满足要求。

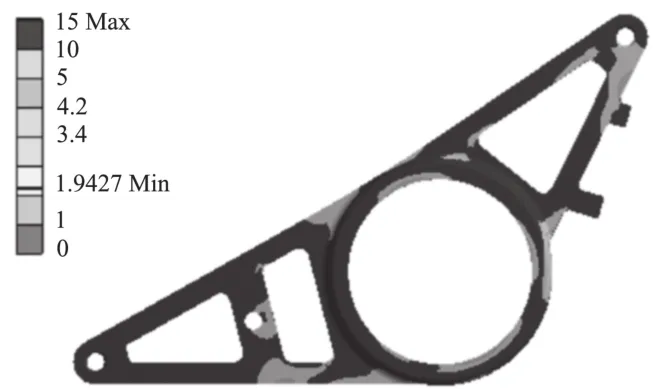
图10 极限工况下差速器支撑架的安全系数

应用Fatigue Tool模块,在工具箱中对寿命、损伤、疲劳敏感度进行求解,得出左支撑架寿命最少可达1×107cycles,在1×109cycles之内未出现损伤。

综上,加速器左支撑架的寿命、损伤和安全系数随载荷的变化稳定且收敛,满足疲劳寿命要求。

3 协同优化

3.1 拓扑分析

对模型进行Shape Optimization模块分析即拓扑分析,得出左支撑架的大致拓扑形状见图11。

图11 左支撑架拓扑分析图

图11中,Remove表示可去,Marginal表示参考,Keep表示不可去。拓扑分析图提供了不能轻易镂空或减去的区域,根据分析结果,镂空形状范围可扩大,在支撑架的边界可采用曲线设计(既减轻质量,也美观),为优化设计提供了可靠依据。

3.2 多参数协同优化

为了不影响传动系统标准件的参数,实现多变量协同优化设计,将支撑架主体作为优化对象。输入参数见图5,输出参数即协同优化目标见表4。

表4 协同优化目标

设置优化目标值为最小安全系数大于1.5、质量最小且最大应力小于160 MPa。然后设置变量变动的上下限,生成130组样本点。选取20个优化变量和4个优化目标的130组样本点进行试验设计,生成130个计算流程,后续可直接进行数据提取。

选择Design Exploration中的响应曲面(Response Surface)进行优化设计分析。响应面构建采用RSO方程,代理模型选择二阶标准响应面构建模式响应面。可直接得到代理模型表达曲面及各参数权重表,基于该响应面代理模型建立优化方程。

利用优化方程,在ANSYS Optimization模块中求得最小安全系数、质量和最大应力间的关系(见图12),获得最佳优化参数方案。

图12 最小安全系数、质量和最大应力间的关系

图12为帕累托解集,所示整个区域为可行域,最高区域为帕累托前沿,是不使任何优化目标劣化的最优参数点集；中间、低层、离散区域包含劣化了的参数点。因此,从帕累托前沿中选用最合理参数方案。

3.3 可靠性检验

在帕累托前沿中选取一个合理方案,为便于后续的加工及装配,将所选参数进行修正、圆整。把优化之后的参数再次进行可靠性分析,等效应力、安全系数分别见图13和图14。

图13 优化后差速器支撑架的主应力分布(单位：MPa)

图14 优化后差速器支撑架的安全系数

由图13、图14可知：多目标协同优化后差速器左支撑架安全系数为1.87,疲劳寿命最少可达1×107cycles,在1×109cycles之内未出现疲劳损伤,满足可靠性要求。

3.4 轻量化对比

优化前后性能对比见表5。

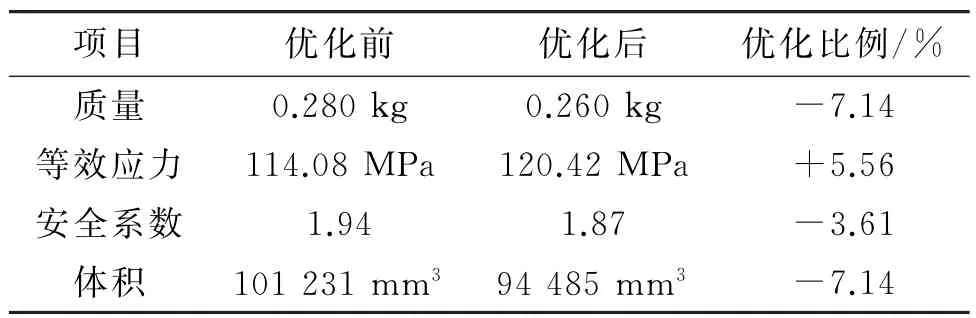
表5 左支撑架优化前后性能对比

支撑架强度、刚度的提高不仅可通过选择更好的材料来实现,结构参数和布局优化更重要。由表5可知：优化设计后,在叠加工况下的最大应力为120 MPa,远小于7075铝的屈服极限455 MPa,且安全系数符合安全标准。通过改进支撑架结构,减轻了质量,提高了材料利用率。

4 结语

在分析计算支撑架垂直面受到的来自链传动的压轴力、支撑架中心处由轴承传递的轴向力的基础上,改进集中受力的结构参数,提高支撑架受载能力,保证协同设计的可靠度。可靠性分析中,充分利用支撑架的结构特性进行模型建立、网格划分,避免结构的无规律及材料浪费。基于二阶标准响应面代理模型建立优化方程,利用优化方程分析20个优化变量和4个优化目标的130组样本点,求得最佳优化参数方案。结果表明,优化后的最大应力值远小于7075铝合金的屈服极限,差速器支撑架质量减少约7.14%,达到了协同优化目标。