基于模糊集与改进证据理论的综合管廊施工安全风险评价

蔡孟龙,胡庆国,何忠明

(长沙理工大学 交通运输工程学院,湖南 长沙 410114)

综合管廊在规划市政管线建设与增强城市综合承载能力方面具有显著优势,能解决地下基础设施建设中路面重复开挖、架空线网过密及管线安全事故频发等问题,还能最大化节约土地资源与最优化利用有限的地下空间资源实现城镇化。但其实施过程中易对周遭环境产生不良影响,并伴随着安全事故的发生,对其施工安全及邻近重要建构筑物安全性影响风险评价已成为城市地下综合管廊建设中十分必要的环节。杜修力等采用证据理论对长春轻轨三期的某地下站深基坑工程施工风险进行了评价；何忠明等通过分析高边坡爆破施工的失稳因素,建立集对可拓模型对广西某高速公路扩建段高边坡爆破施工安全风险进行了评价；刘艳宇等建立基于层次分析法的模糊评价模型,对某综合管廊PPP项目风险管理进行了研究；张胜昔等构建G－FAHP评价模型,对青岛某深基坑施工风险进行了综合评价,并对关键风险要素进行了排序。目前针对城市地下综合管廊项目的风险评价大多以PPP项目全生命周期为出发点,且在大多数定量评价中会涉及专家打分,会受到专家主观意见和自身经验等不确定因素的影响。该文将模糊集与改进D－S证据理论相融合,建立综合管廊施工安全风险评价模型,对城市地下综合管廊施工安全风险进行全面评价。

1 理论简介

1.1 模糊集理论

模糊集理论采用隶属函数表示不确定概念外延中对象属于概念的程度。采用高斯隶属函数反映正态分布特征,即：

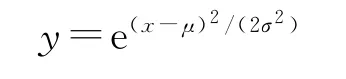
式中：μ为函数的中心；σ为宽度,其值与专家意见的确信度成反比。

1.2 D-S证据理论

Dempster教授提出利用多值映射思想来界定不确定概率的上、下界。由合成法则可知,n个独立证据m1,m2,…,mn的融合结果为：

2 风险评价指标体系

2.1 评价指标体系的建立

由于综合管廊是在地下建设,其基坑工程和主体工程具有复杂性、综合性且易受周边环境的影响。参考GB 50838－2015《城市综合管廊工程技术规范》、GB 51354－2019《城市地下综合管廊运维级安全技术标准》等,结合问卷调查法,充分考虑其缆线、干线、支线及干支混合等4种设计类型,选取5个主要影响因素构建综合管廊施工安全风险评价指标体系(见表1)。

2.2 综合管廊施工安全风险等级划分

在查阅大量建筑、公路、市政工程等评价文献的基础上,结合综合管廊项目的特点,按照李克特量表的形式,将综合管廊施工安全风险评价指标的等级评语按照高低分为VL、L、M、H、VH 5个等级,其值分别为θ1、θ2、θ3、θ4、θ5,构成评语集合 Θ＝{θ1,θ2,θ3,θ4,θ5}。风险等级划分见表2。

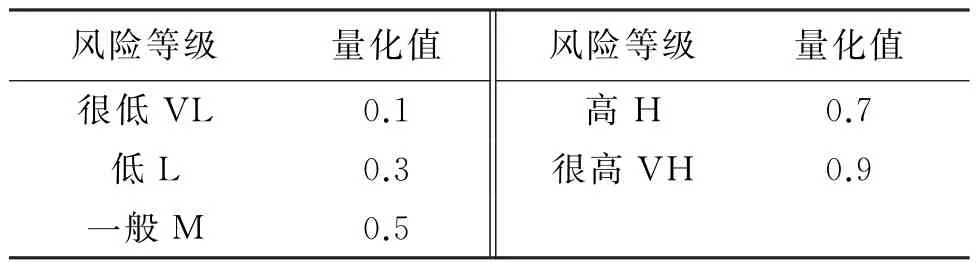
表2 综合管廊施工安全风险等级

3 综合管廊施工安全风险评价模型

3.1 权重的确定

引入连续有序加权平均算子COWA确定权重,运算步骤如下：

(1)指标A i决策数据集结为(a i1,a i2,…,a in),根据其数值大小对数据重新进行递减排序,并将新集结数列重新编号为(b i1,b i2,…,b in)。

(2)利用组合数计算b i的权重,求加权向量：

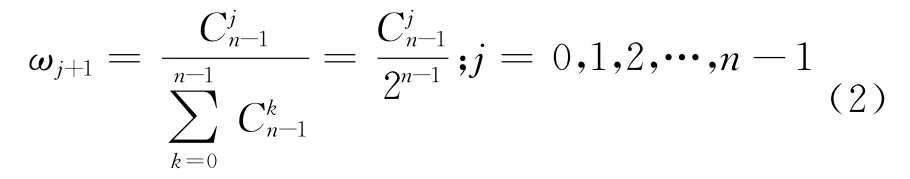
(3)按下式计算A i的绝对权重

(4)按下式计算指标A i的相对权重ωi：

式(4)所得即为指标的COWA权重值。

3.2 隶属度矩阵的建立

由隶属度求出各指标隶属于不同风险等级的程度。定义中心点μ＝(0,0.25,0.5,0.75,1),则隶属度函数如下：

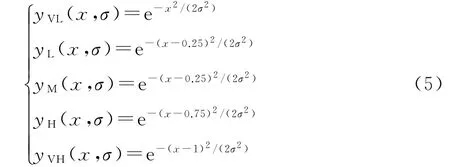
按式(5),结合各评价指标构造隶属度矩阵如下：

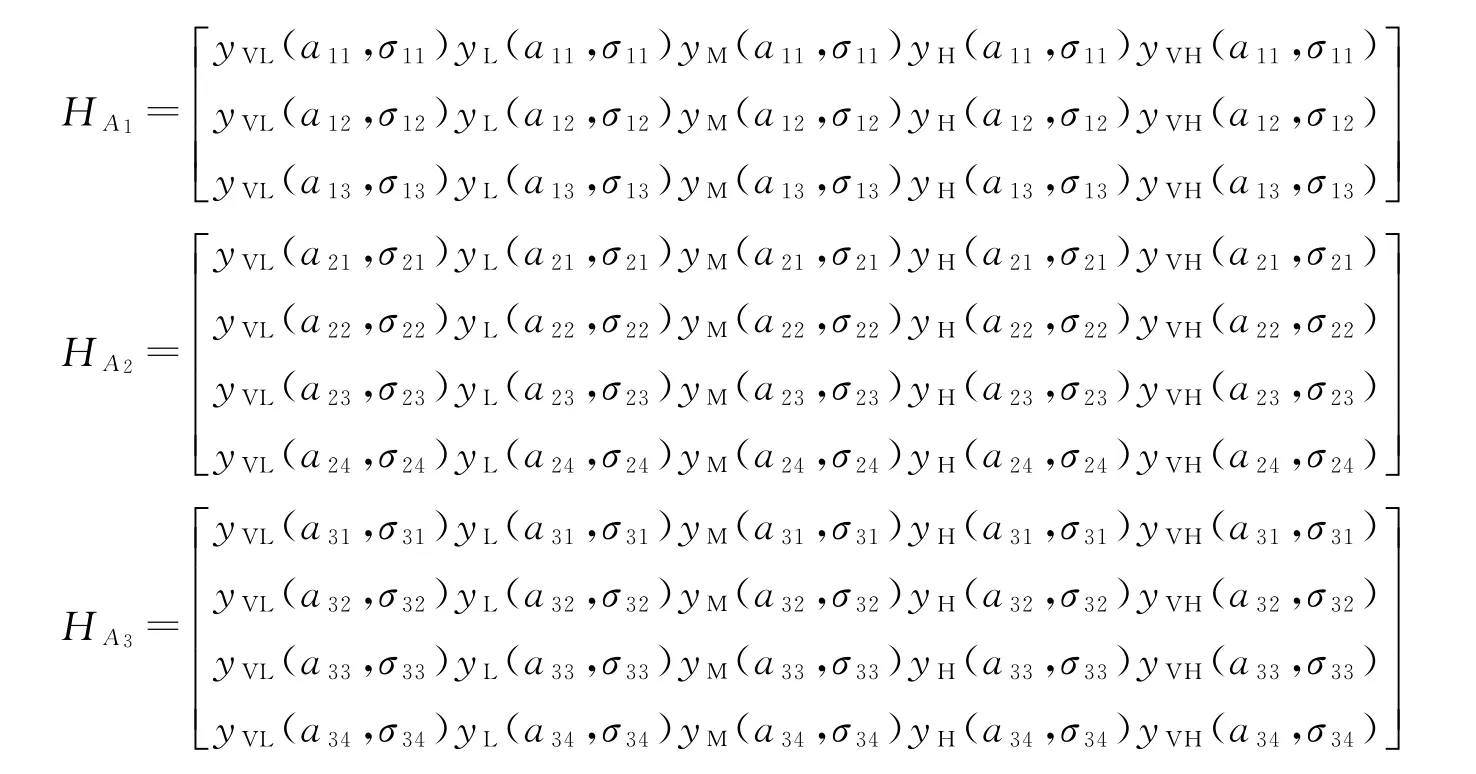
3.3 证据融合

依据传统D－S证据理论中的Dempster合成法则可对数据进行融合,但证据之间的冲突程度越大,其算法缺陷逐渐突出,特别是当冲突较高时,融合结果可能不太符合实际。根据文献[10],证据间的互相冲突对决策评价而言并非全都是无用的。综合管廊施工安全风险分为5个等级,融合n位专家意见时所需的计算量随着专家人数呈指数增长。为提高高冲突下证据融合的合理性与真实性,引入基于权值分配与矩阵分析的算法,具体运算过程参考文献[11]～[12]。基于权值分配与矩阵分析的D-S合成算法流程见图1。

图1 基于权值分配与矩阵分析的D-S合成算法流程

3.4 mass函数合成

对所有指标函数按下式进行数据融合：

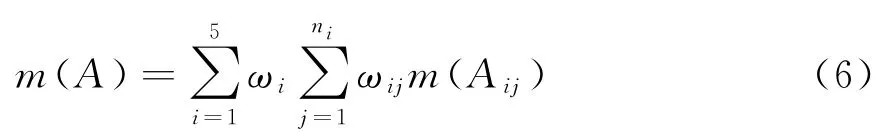
式中：m(Aij)为指标Aij对A的支持度,通过转化专家意见后得到；ni为指标Ai所含子指标的个数。

3.5 风险综合评价

根据统计学与概率学原理,风险评定的每一等级的概率大小在理论上是相等的,为使评价结果一目了然,将综合管廊施工风险评价等级的取值范围定为[0,1],并以此划分5个等级(见表3)。

表3 综合管廊施工安全风险等级划分

将合成后的风险等级概率分配矩阵P与表2中的评价量化值U相乘,并进行单值化,得到风险综合评价结果。

4 实例分析

4.1 工程概况

重庆市开州区地下综合管廊建设一期项目起于滨湖北路丰太段K0＋000,止于滨湖北路大丘段K6＋091,全长6 091 m。其中：K0＋000—K4＋180段管廊基坑长度4 180 m,自然放坡,坡比1∶1.5,基坑深度8～13 m,采用分层明挖施工；K5＋180—K6＋091段管廊基坑长度911 m,桩板挡墙支护,基坑深度8 m,采用分层明挖施工；K4＋180—K5＋180段管廊基坑长度1 000 m,锚喷支护,基坑深度4.8 m,采用分层明挖施工。综合管廊采用矩形箱涵结构形式,分为两舱和三舱,断面净空尺寸分别为(1.6＋4.2)m×2.8 m、(2.1＋1.6＋2.6)m×2.8 m～(2.1＋1.6＋4.2)m×2.8 m,设置监控中心一座(见图2)。

4.2 指标权重的确定

通过调查问卷请6位从业人员对指标A1～A5的重要度进行打分,运用COWA算子确定各指标的权重。以A1为例,按式(2)求得加权向量,根据式(3)计算绝对权重,得：

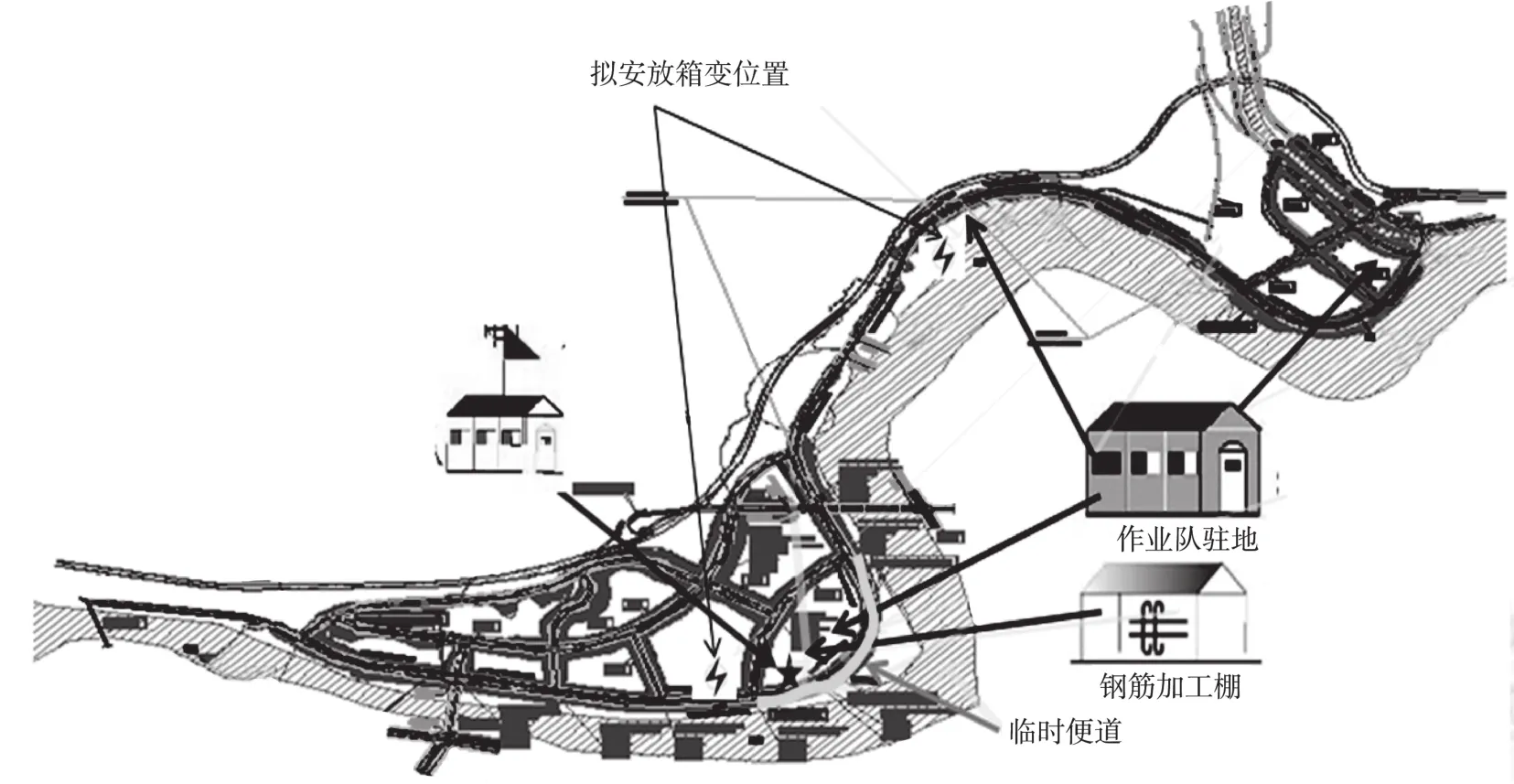
图2 重庆市开州区地下综合管廊平面布置

4.3 风险综合评价

为确保评价结果真实有效,邀请3位具有丰富经验和高级职称的评委(2位为某地综合管廊项目的项目经理,1位为当地高校的教授)对该项目的施工安全风险进行评价,并将其评价意见带入隶属度矩阵进引计算,归一化后得表4～6。

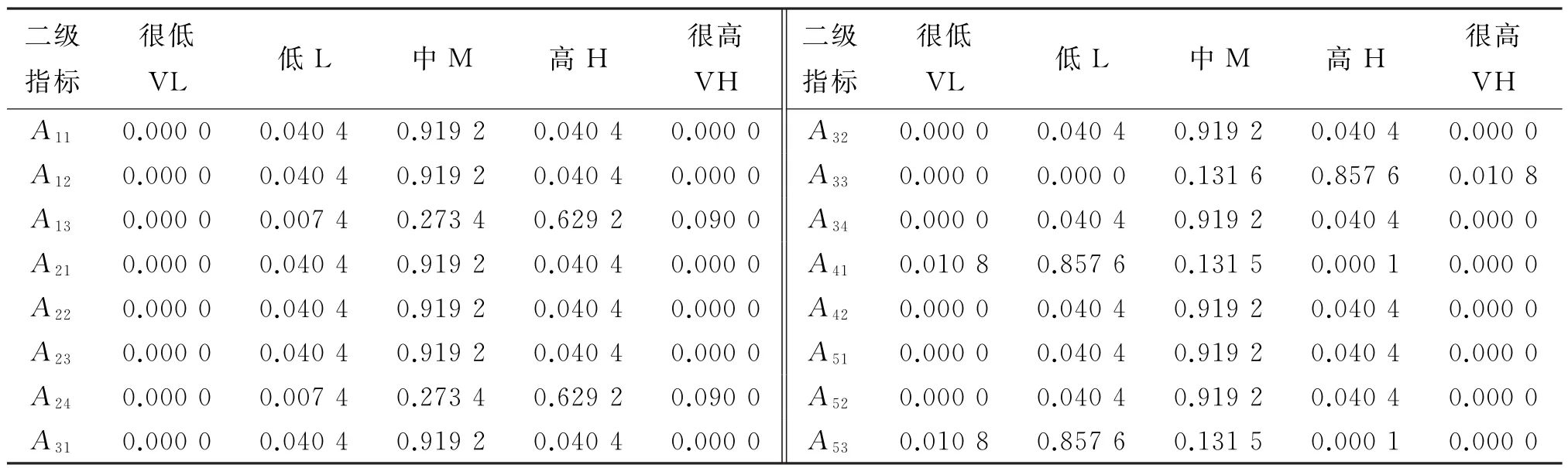
表4 专家1基本概率分配

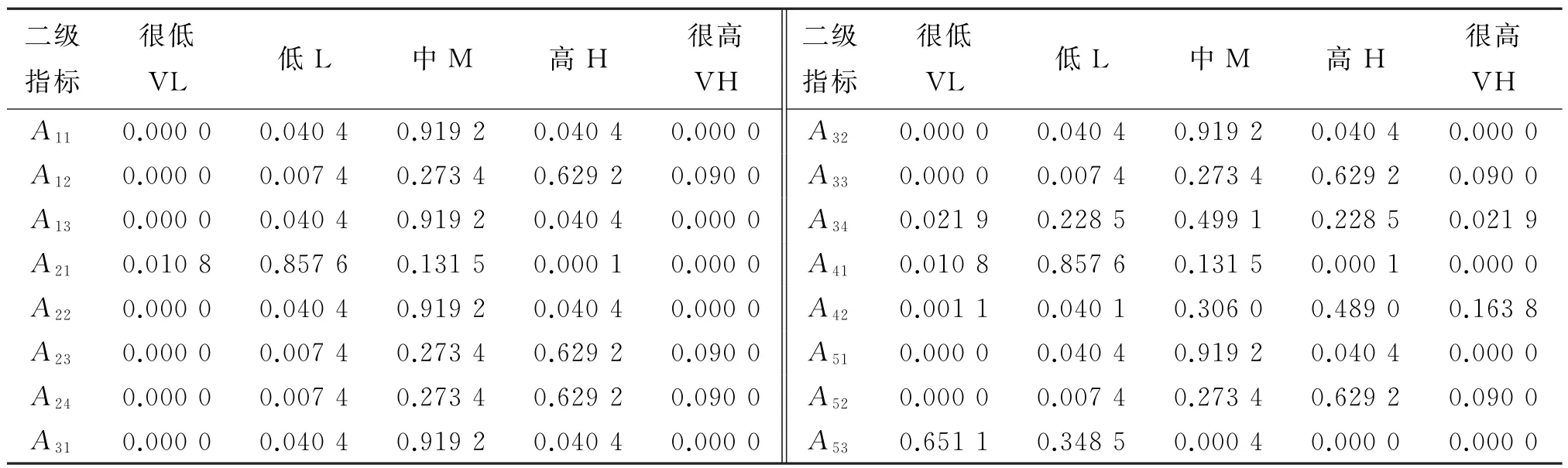
表5 专家2基本概率分配

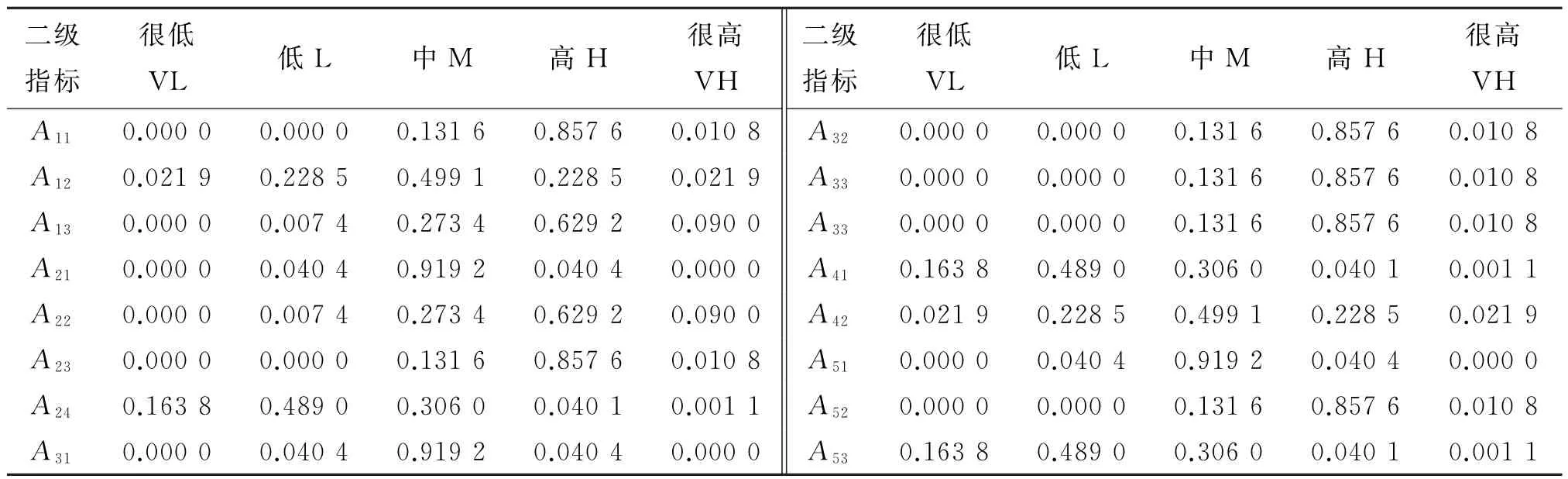
表6 专家3基本概率分配

采用图1所示D－S证据合成算法融合上述3位专家的基本评价概率,结果见表7。

表7 基于改进D-S证据理论的数据融合结果

根据式(3)和COWA算子所得各层指标权重,将表8所示指标数据输入MATLAB软件进行逐层合成,结果见表8。

表8 各层指标Mass函数合成

综合评价值R＝P×U＝0.496 2。由表3可知：开州城市地下综合管廊施工安全风险为中等。为分析各指标对综合管廊施工安全风险的影响大小,将指标A1～A5进行单值化处理,得指标风险值如下：R1＝0.544 1,R2＝0.541 2,R3＝0.528 2,R4＝0.382 8,R5＝0.454 4。将上述指标风险值按照大小进行排序,R1＞R2＞R3＞R5＞R4,说明在综合管廊施工安全风险中,人为因素与设计因素是较主要、影响较大的两个因素。该综合管廊项目各施工人员具有相应的资质,负责安全管理的专职人员能及时指出危险操作并要求防范；舱数、断面尺寸、分区投料口设置合理；在进行深基坑分层明挖施工时,根据各标段的边坡土质特性,分别采用桩板挡墙与喷锚等支护方法,可有效避免险情发生,安全风险为中等风险。

5 结论

(1)针对施工安全风险评价中专家意见不集中等问题,建立基于模糊集与改进D－S证据理论的城市地下综合管廊施工安全风险综合评价模型,通过将模糊集与证据理论相结合,真实可靠地反映综合管廊施工中的不确定性,提高风险评价的准确度,且该评价模型逻辑清晰、计算简单、易于推广。

(2)基于COWA算子的权重计算与传统层次分析法、德尔菲法相比更严谨、客观,可降低专家评价主观因素的影响。采用以高斯函数为隶属度函数构造Mass矩阵,并与权值分配和矩阵分析算法相结合,所得结果比传统证据理论更准确。

(3)重庆开州区地下综合管廊建设一期项目的施工安全风险为中等,与工程实际吻合度较高,验证了该量化模型的正确性与可实践性,可为项目的顺利进行提供有力保障。