基于模糊逻辑的异形拱塔斜拉桥黏滞阻尼器参数优化研究

邹辉煌，张谢东，王琛，黄笑犬

(武汉理工大学 交通学院，湖北 武汉 430063)

地震作为一种常见自然灾害，对桥梁等结构破坏作用巨大。桥梁是交通运输的枢纽，一旦被破坏，会对社会经济建设与发展造成巨大的损失。所以对斜拉桥抗震性能的研究，保证其震后功能正常使用及结构完整具有十分重要的意义。

黏滞阻尼器作为一种常用减震耗能装置，具有装置简单、安全、经济效益高、易于维修更换且减震效果好等优点，被大量应用于结构减震。黏滞阻尼装置在斜拉桥减震研究中已取得很多成果。如AK Agrawal通过黏滞阻尼器对斜拉桥位移、弯矩减震研究得出黏滞阻尼器能高效减小桥梁结构响应的结论；贾帅以某双塔斜拉桥为对象，对设置黏滞阻尼器与不设置黏滞阻尼器两种方案进行对比，得出设置阻尼器可大幅降低主梁位移及塔底弯矩的结论；Wen LiangQiu、Jin Zhu等以斜拉桥为对象，研究了黏滞阻尼器阻尼系数以及速度指数对结构减震的影响，为该桥选出了合适的阻尼器参数；游瀚以某斜拉桥为对象，对黏滞阻尼器横向减震进行研究，速度指数取0.3、阻尼系数取2 500 kN·(s/mm)时该桥主梁位移及塔底弯矩达到最佳减震效果；梁智垚以某大跨公铁两用斜拉桥为例，对黏滞阻尼器参数进行分析，当速度指数取0.4、阻尼系数取10 000 kN·(s/mm)时该桥减震效果最佳；王雷以某低塔斜拉桥为研究背景，对黏滞阻尼器装置参数进行分析，阻尼系数为3 000 kN·(s/mm)，速度指数为0.4时该桥减震效果达到最佳。

黏滞阻尼器作为一种广泛使用于桥梁中的减震装置，在常规桥梁中黏滞阻尼减震性能得到大量研究，但异形斜拉桥结构特殊，实际工程较少，使得异形斜拉桥黏滞阻尼减震性能的研究较少。该文以某异形拱塔斜拉桥为对象，建立全桥三维有限元模型研究黏滞阻尼参数对该桥减震效果的影响，并运用Matlab模糊逻辑优化，得到综合减震性能最佳时的阻尼参数，为该异形拱塔斜拉桥黏滞阻尼器抗震参数的选取提供参考。

1 背景工程及有限元建模

该文以某异形拱塔斜拉桥为工程背景，研究黏滞阻尼参数对该桥减震性能的影响。该异形拱塔斜拉桥主桥跨径布置为2×70 m；主梁为带挑梁的钢箱梁结构；索塔采用花瓣形边、中桥塔布置，桥塔外形均为半椭圆拱形塔，两侧边塔相对竖直中塔外倾30°，边塔桥面以上高35 m，中塔高30 m，边、中塔均采用矩形钢箱截面，通过拱脚预埋段与下部桥墩固结，边、中塔之间及边塔与主梁之间均采用空间拉索相连，斜拉索通过钢锚箱锚定在索塔上，全桥共12对主梁斜拉索，12对塔间斜拉索。该桥采用Midas2015有限元分析软件以顺桥向为x轴，横桥向为y轴，竖向为z轴建立三维全桥有限元模型，如图1所示。

图1 全桥有限元模型

主副塔、主梁、横梁、墩身、承台、桩基均采用梁单元模拟，斜拉索采用空间桁架单元模拟。考虑斜拉索初始张拉内力，采用Ernest公式计算斜拉索等效弹性模量考虑拉索垂度引起的非线性问题。主梁采用单主梁模式，主梁与斜拉索、主副塔与桥墩之间均采用刚结；主梁与桥墩之间弹性连接限制横桥向与竖向的位移，释放顺桥向约束，允许主梁出现较大顺桥向位移，形成漂浮结构体系。桩基础采用m法参考JTG D63-2007《公路桥涵地基与基础设计规范》相关方法计算土弹簧刚度，模拟桩土间的相互作用。在主梁与横梁相交处，沿纵向设置1个黏滞阻尼器，黏滞阻尼器的阻尼系数C取值2 000～5 000 kN·(s/mm)，间隔500 kN·(s/mm)；速度指数α取值0.2～1.0,间隔0.2，共设置35种组合。

2 黏滞阻尼减震性能分析

2.1 黏滞阻尼减震原理

黏滞阻尼器是一种被广泛采用的减震耗能装置，一般由缸筒、活塞、阻尼通道、阻尼介质(黏滞流体)和导杆等部分组成。桥梁等建筑结构由于地震等因素产生变形时，黏滞阻尼器的活塞杆发生运动，黏滞液体由于受到活塞杆的拉压而从活塞上的小孔阻尼通道内流过产生阻尼，如此的往复运动消耗地震等因素对桥梁结构输入的能量，达到减小结构动力响应的目的。

黏滞阻尼器基本力学方程如下：

F=CVα

(1)

式中：C为阻尼系数[kN·(s/mm)]；F为阻尼力(kN)；V为活塞杆速度(mm/s)；α为速度指数。速度指数α实际取值范围为0.1～2.0，在土木工程结构中一般取值范围为0.2～1.0。当α为1时，该阻尼器为线性阻尼器，恢复力滞回曲线近似椭圆；α不取1时为非线性阻尼器，一般情况下α取值越小滞回曲线越饱满，耗能越大，其形状近似矩形。

2.2 减震性能分析

该文依据桥址地质报告，抗震设防烈度为7度，加速度为0.1g，场地类别为Ⅱ类，特征周期0.4 s。根据GB 50011-2001《建筑抗震设计规范》选取两条天然地震波及一条人工拟合地震波对该桥模型进行时程分析。斜拉桥在地震作用下，一般在主梁处会产生较大位移，塔底处产生较大弯矩。由于所研究异形拱塔斜拉桥桥塔结构外形独特，该文将对主副塔塔顶位移、主梁位移及主副塔底部弯矩进行对比分析。

为从3种波中选出对结构产生最不利影响的地震波。该文以主塔顶部位移时程及副塔底部弯矩时程为例，对比3种波对该桥动力响应的影响。主塔顶部位移时程曲线及副塔底部弯矩时程曲线如图2所示。

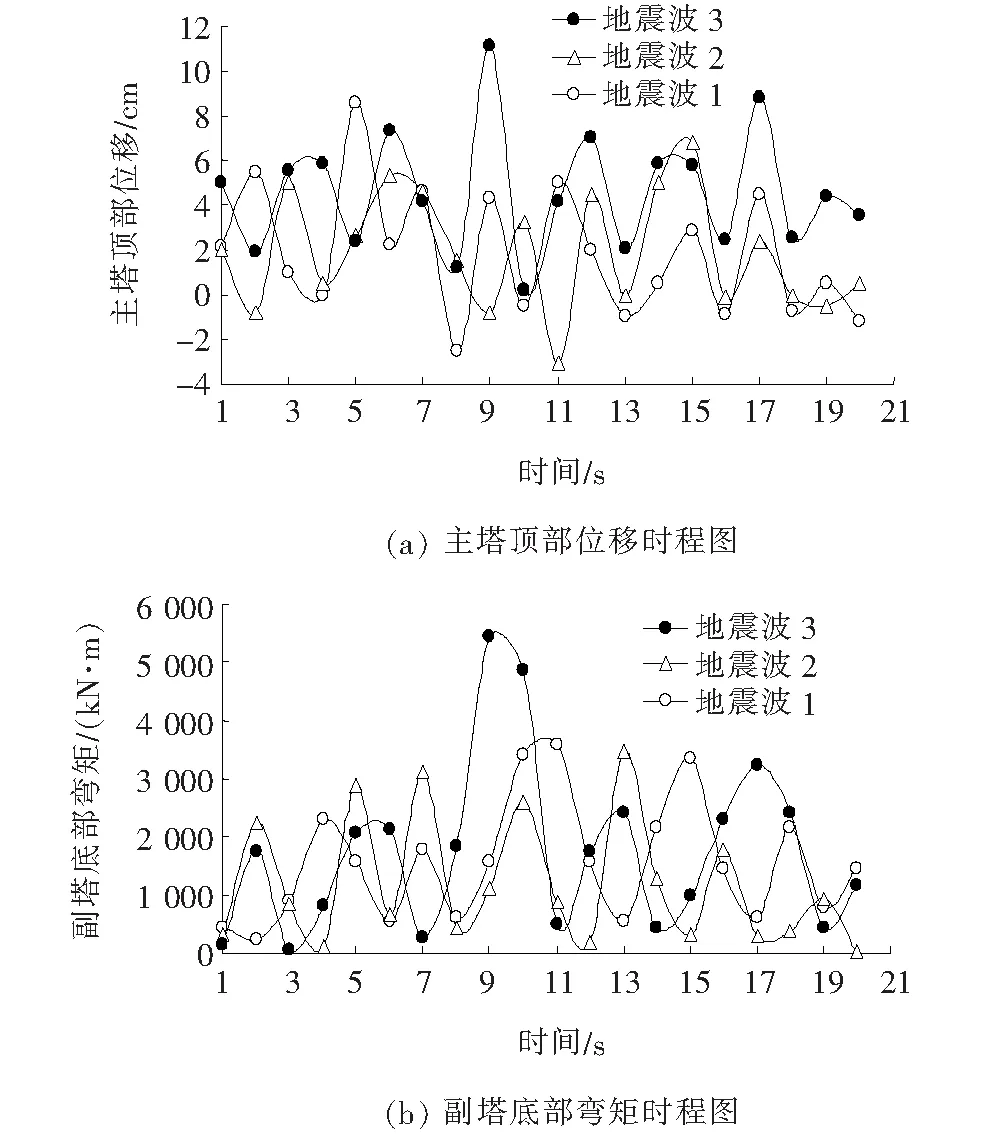
图2 动力响应结果

由图2可知：在3种地震波作用下，地震波3在9 s左右时对该桥产生的动力影响最大。因此后文将以地震波3为最不利地震荷载，研究黏滞阻尼器对该桥抗震性能的影响。

在地震波3作用下，保持阻尼系数C取3 500 kN·(s/mm)不变，改变速度指数，各工况关键位置位移及弯矩变化趋势如图3所示。

由图3可以看出：① 阻尼相同时，在地震荷载作用下，左主塔顶部产生的位移均最大，主梁产生的位移均最小；设置阻尼后，主梁与桥塔的位移量均减小，减小幅度相差不大；② 阻尼相同时，在地震荷载作用下，主塔底部产生的弯矩均较大，副塔底部产生的弯矩均较小；设置阻尼后，主、副塔的弯矩均减小，主塔弯矩减小幅度较小，副塔弯矩减小幅度较大。

图3 关键部位位移、弯矩随速度指数的变化规律[C=3 500 kN·(s/mm)]

设置阻尼器后，主副塔顶及梁端位移均得到了有效的减小，且主塔顶部位移最大，选取主塔顶部位移为第1个优化控制变量。设置阻尼器后，主、副塔塔底弯矩均减小，但阻尼器对主塔塔底弯矩减小幅度较小、不明显，对副塔塔底弯矩减小幅度较大，选取副塔塔底弯矩为第2个优化控制变量。主塔顶部位移及副塔底部弯矩在不同阻尼系数C及速度指数α共35种参数组合下的数据变化趋势如图4、5所示。

从图4可以看出：① 设置阻尼器后，当α不变时，主塔塔顶位移大致随阻尼系数C的变大而变小，但是在α取0.2时，随着阻尼系数变大，主塔塔顶位移先减小后变大；② 当C不变时，主塔塔顶位移大致随着速度指数α的变大而变大，但是在阻尼系数C取5 000 kN·(s/mm)时，随着速度指数的变大，主塔塔顶位移先减小后增大。

从图5可以看出：① 设置阻尼器后，当α不变时，副塔底部弯矩大致随阻尼系数C的变大而变小；② 当C不变时，在C小于3 500 kN·(s/mm)时，随速度指数的变大，副塔底部弯矩先减小后增大；在C大于4 000 kN·(s/mm)时，随速度指数的变大，副塔底部弯矩大致变化为先增大后减小再增大。

图4 主塔顶部位移随C、α的变化规律

图5 副塔底部弯矩随C、α的变化规律

设置黏滞阻尼装置后，总体大致变化趋势是随着阻尼系数的增大，塔顶位移及塔底弯矩均会减小；随着速度指数的增大，塔顶位移及塔底弯矩均会增加。故对该桥进行减震设计时宜选取阻尼系数大、速度指数小的黏滞阻尼器。

3 模糊逻辑参数优化

3.1 变量隶属函数

从以上分析结果可知阻尼系数大、速度指数小的黏滞阻尼器对该异形拱塔斜拉桥减震效果良好，但阻尼参数对塔顶位移及塔底弯矩影响变化规律存在不一致的情况，难以找到精确的数学函数对其进行分析计算，无法直接找到最优阻尼参数。模糊逻辑作为一种模糊数学方法，不需要精确的数学模型，可通过专家经验制定模糊控制规则对问题进行求解，且这种方法具有很强的鲁棒性、适应性及很好的容错性。因此该文拟采用模糊逻辑控制理论，运用Matlab Fuzzy Logic模糊工具箱，选取隶属度函数，定义主塔顶部位移减震率γ以及副塔底部弯矩减震率β为输入量，综合减震性能k为输出量，对其进行参数优化研究。主塔顶部位移减震率及副塔底部弯矩减震率具体含义见式(2)：

(2)

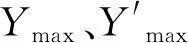
利用式(2)计算可得主塔顶部位移减震率γ以及副塔底部弯矩减震率β结果如表1所示。

表1 主塔顶部位移减震率及副塔底部弯矩减震率结果

主塔顶部位移减震率γ、副塔底部弯矩减震率β、综合减震性能k模糊处理，分为5个评价等级：差、较差、中等、较好、好。选择合适的隶属度函数时，在结果误差较小时选择分辨率较高的函数，即较尖的函数；结果误差较大时可选择分辨率低较平缓的函数。该文均采用分辨率较高的trimf三角函数为隶属函数。隶属函数表达为：

y=trimf[x(a,b,c)]

(3)

式中:a、b、c为隶属函数的形状参数，a、b为三角形下部两顶点，c为三角形顶部顶点。

3.2 模糊优化结果

依据经验制定输入变量与输出变量之间模糊规则查询表，根据模糊规则运用Matlab模糊工具箱，求得弯矩、位移、综合减震性能之间的模糊关系见图6。

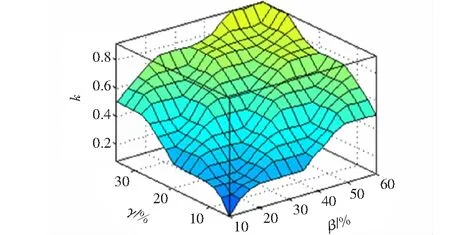
图6 综合减震性能与位移、弯矩模糊关系

图6结果显示：经Matlab模糊优化所得结果具有一定的变化规律，优化结果理想，综合减震性能总体趋势随着主塔顶部位移减震率及副塔底部弯矩减震率的增大而增大，且具有很好的正相关性。在Matlab中输入表1中主塔顶部位移减震率和副塔底部弯矩减震率数据，可得到黏滞阻尼综合性能与阻尼系数C与速度指数α之间的关系，具体结果见表2。

表2 综合减震性能k

由表2可知：经模糊逻辑处理，综合减震性能k总体趋势随阻尼系数的增加而增加，随速度指数的增加而减小，变化趋势较为明显。由表可得：在阻尼系数C取4 500 kN·(s/mm)，速度指数α取0.2时，综合减震性能效果最好为0.794，此时主塔顶部位移与副塔底部弯矩综合减震效果达到最佳，经查表1可知：此时主塔顶部位移减震率达到31.27%，副塔底部弯矩减震率达到52.77%。

在地震荷载作用下，无阻尼及阻尼系数C取4 500 kN·(s/mm)、速度指数α取0.2时，前20 s主塔顶部位移、副塔底部弯矩时程变化如图7所示。

图7 有、无阻尼器地震响应对比

从图7可以看出：主塔顶部最大位移及副塔底部最大弯矩在9 s左右出现，安装阻尼器后，最大位移及弯矩均得到有效控制，且最大弯矩得到大幅度减小。安装该阻尼器后减震效果明显，可有效降低该异形拱塔斜拉桥的地震响应。

4 结论

该文以异形拱塔斜拉桥为对象，建立全桥三维有限元分析模型，研究了黏滞阻尼器参数对异形斜拉桥抗震性能的影响，并运用Matlab模糊逻辑对黏滞阻尼器减震参数进行了优化。得到以下结论：

(1) 在地震作用下，设置黏滞阻尼器后，该异形塔斜拉桥主、副塔顶部位移，梁端位移，主、副塔底部弯矩均得到有效减小。设置黏滞阻尼器后能有效减小该异形塔斜拉桥的地震反应，提高该异形塔斜拉桥的抗震能力。

(2) 异形拱塔斜拉桥动力响应随阻尼参数的变化规律为：当速度指数不变时，随阻尼系数的增大，塔顶位移及塔底弯矩均减小；当阻尼系数不变时，随速度指数的增大，塔顶位移及塔底弯矩均增加。对该桥进行减震设计时宜选取阻尼系数大，速度指数小的黏滞阻尼器。

(3) 运用Matlab模糊逻辑优化得出结论：当阻尼系数C取4 500 kN·(s/mm)、速度指数α取0.2时，综合减震性能效果最好为0.794，主塔顶部位移与副塔底部弯矩综合平衡减震效果达到最佳，减震率分别为31.27%、52.77%。