智能压实间接指标试验分析与压实度预测
2020-06-05黄国卿严筱杨永刚牛迪
黄国卿, 严筱, 杨永刚, 牛迪
(云南省交通规划设计研究院有限公司,云南 昆明 650041)
压实度是路基施工过程中最重要的指标之一,路基压实度不足或压实不均匀容易造成工后差异沉降,进而导致路面出现裂缝、凹陷等病害。传统的压实度主要通过环刀法、灌砂法等手段进行“点”检测,效率低、全面性差及时效性差等问题突出。智能压实是根据土体与振动压路机相互动态作用原理,基于连续量测振动压路机的响应信号,采用压实质量实时评估指标来实现对整个碾压“面”压实质量的动态监测与控制。压实强度和均匀性的判定是智能压实系统的重要内容,而智能压实指标是该系统中的关键。
20世纪80年代以后,路基连续压实检测技术逐渐成为国际研究热点,瑞典、德国、美国、日本、中国等国家都相继研发了相应的检测系统。目前,智能压实指标主要分为经验反应类的间接指标和基于力学模型的直接指标,前者代表性的有压实密度值CMV、连续压实值CCV及谐波总失真THD等,后者有动态模量及动态刚度。一般的经验反应类间接指标都是基于振动轮中心处垂向加速度,由于信号获取相对简便,且无需复杂的力学模型,目前该类指标在智能压实中应用广泛,代表性的有瑞典Dynapa公司、德国Bomag公司、日本Sakai公司等。但理论研究和实际应用均表明,智能压实间接指标与传统压实度的相关性不高,且多数研究侧重于压实强度的评价,关于表征压实均匀性的研究较少。
该文在分析连续智能压实系统组成的基础上,首先介绍了3种智能压实间接指标的计算方法。同时,通过现场试验,对比分析各指标表征不同压实遍数下土体压实强度和均匀性的能力;最后,基于3个智能压实间接指标,提出采用BP神经网络预测土体压实度的方法,以提高智能压实间接指标的工程适用性。
1 连续智能压实系统组成
基于智能压实间接指标的连续智能压实系统如图1所示。主要分为信号采集、信号预处理、间接指标计算及压实效果评价4个部分。
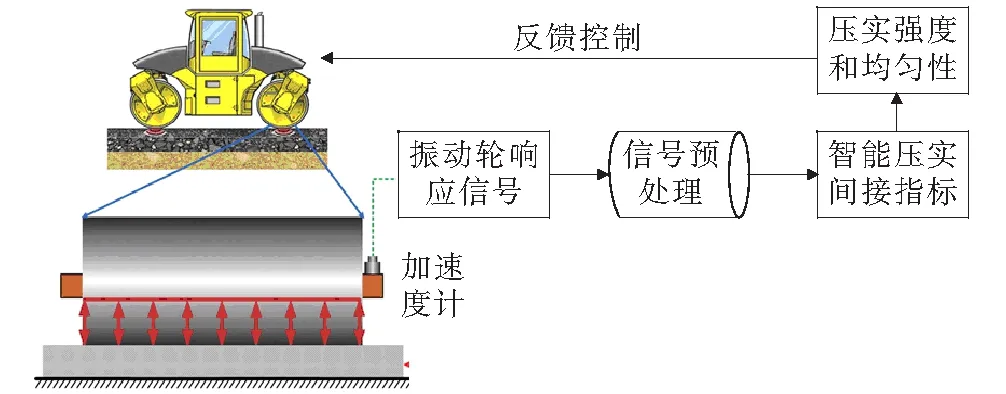
图1 连续压实控制体系
(1) 信号采集:将加速度计固定安装在振动轮的中心,实时采集压路机工作时的振动轮响应信号。
(2) 信号预处理:压路机的启动停止等会带给振动信号一定的噪声和误差。振动信号预处理可以得到真实振动压实信号。预处理工作主要包括预滤波、零均质、错点剔除以及消除趋势项等。
(3) 间接指标计算:将预处理后的信号作为输入源,通过响应的算法计算智能压实间接指标CCV、CMV和THD值,各指标的定义和计算将在下文给出。
(4) 压实效果评价:基于采集的智能压实间接指标,通过压实的强度和均匀性两个方面分别评价压实的效果,进而对土体压实过程进行反馈控制。
2 智能压实间接指标
振动加速度信号在空振的情况下呈正弦周期信号,但当土体对振动轮产生抵抗力时,振动加速度信号出现畸变,土体压实程度越大畸变越明显,加速度信号的谐波分量也越多。基于此原理,智能压实间接指标通过谐波比值大小来反映路基压实程度的振动响应。
(1) 压实密度值CMV
瑞典Dynapa公司认为振动轮信号频率中除了基频信号外,一次谐波成分占了主要部分,定义压实密度值CMV为基频幅值a(w0)与二次频幅值a(2w0)的比值来反映信号的畸变程度,如式(1)所示:
(1)
式中:C为一个静态量,根据实际情况标定,通常取C=300。CMV为一个无量纲的相对值,CMV越大,表明土体的压实度越好。但由于实际上土体对压路机钢轮的作用不仅仅体现在二次频信号上,可能还有其他的谐波,故CMV值一般只适用级配较为单一的路基土,具有一定的局限性。
(2) 连续压实值CCV
日本曾对瑞典的压实计法进行过较细致的研究,发现振动响应信号频谱成分极具复杂性,CMV在很多情况下并不能正确反映填筑体的压实程度。因此,考虑多次谐波成分的连续压实值CCV更适用于复杂级配的土体,如式(2)所示。CCV越大,表明土体的压实度越好。然而,CCV值只是将不同谐波的振幅进行了简单的累加,因此该指标更适用于畸变信号明显的场景,在压路机弱振状态下具有明显的缺点。
CCV=
×100
(2)
(3) 总谐波失真THD
Mooney提出总谐波失真THD可作为填料压实状态的评价指标,THD是碾压轮n次谐波分量振幅的均方根与基波振幅的比值,定义如式(3)所示:
(3)
式中:a(w0)为加速度频谱中的基频振幅;a(nw0)为加速度频谱中的n次谐波分量振幅。
总谐波失真THD越大,碾压轮加速度的谐波分量越多,表明土层越坚硬,压实程度越高。但是,THD的n值并未明确给定,且该指标错失了半谐波,对于含有刚性下卧层的路基土适用性较差。
3 智能压实间接指标试验分析
3.1 实例描述
选用国产单钢轮振动压路机开展路基土碾压试验。试验对象为上海市宝山区某交叉口的新翻待碾杂填土,土质松散较为均匀,属于黏性土。选取现场50 m×6 m的矩形作为压路机的活动区域。
3.2 试验场景
采用环刀法测量土体的传统压实度,试验方案为每隔5 m放置一个采样点,压路机每碾压一遍取一个环刀。试验选取了8个样本点,碾压3遍,一共收集24个有效样本。
在试验中,记下压路机压过标记点的绝对时间,读取传感器数据中该时刻前后0.2 s内的加速度序列作为该点的压实振动反应,并处理后得到智能压实的间接指标。
3.3 结果分析
3.3.1 不同压实遍数
为了横向比较不同智能压实间接指标在压实遍数后的状态,对收集的数据进行归一化处理:
(4)
式中:X为智能压实间接指标序列集合;x为序列集合的元素;x′为x归一化后的数据。
CMV、CCV和THD3个间接指标归一化后随压实遍数的分布如图2所示。在振动碾压轮作用下,土颗粒越来越紧密,土体的密实度越来越高,因此随着压实遍数的增加,土体的压实度也增大。相邻的碾压遍数之间,如果归一化后间接指标的差值越大,则表明该指标能表征压实状态的能力越强。,整体上看,CMV、CCV和THD都基本能区分土体的不同压实遍数,但THD指标在第2遍和第3遍的折线存在部分交织,故该指标的性能比CMV和CCV更差。CMV和CCV指标普遍呈现第2遍和第3遍之间的差值,比第1遍和第2遍更高的趋势,表明振动压路机对土体的第3遍碾压效果最好。
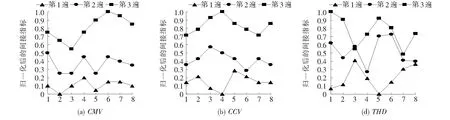
图2 不同压实遍数对智能压实间接指标的影响
3.3.2 不同的间接指标
智能压实间接指标与传统压实度之间的关系如图3所示。由图3可见:① 3个间接指标随着传统压实度的增加而呈现增加的趋势。从定性上看,3个间接指标都基本能描述传统压实度的变化;② 用线性模型拟合这3种趋势,不同间接指标与传统压实度之间的相关性不同,3个指标的相关系数表明对于该文试验的黏性土而言,整体上CMV的相关性最好,CCV次之,THD最差;CMV和CCV在第3遍(高压实度)采集的数据较为离散,而THD在第1遍(低压实度)采集的数据较为离散。这是因为土的性质、碾压遍数都将影响土体对振动轮的抵抗力,导致加速度信号的畸变程度不同,进而影响各个间接指标。因此,在智能压实间接指标实际使用时,应该尽可能多取样进行相关性标定,且应该根据不同性质的碾压土选取更为合适的间接指标。

图3 智能压实间接指标与传统压实度之间的关系
3.3.3 压实均匀性
压实不均匀将导致路基在行车荷载作用下的不均匀沉降,因此同一路基填筑区域的压实均匀性非常重要。在同一区域内,可采用压实同一遍的压实指标变异系数描述压实的均匀性。变异系数越小,表明区域内各点的压实差异越小,则均匀性就越好,工后差异沉降的概率就越小。变异系数C的计算如式(5)所示:
(5)
式中:s为同一区域、压实同一遍后的压实值标准差;u为平均值。
表1为不同压实遍数下各压实指标的变异系数。

表1 不同压实遍数下各指标的变异系数
由表1可见:随着压实遍数的增加,传统压实度的变异系数呈现越来越小的趋势,到第3遍的变异系数仅为0.015,这表明只要压路机行驶路径覆盖均匀,通过控制压实遍数可控制土体压实的均匀性。同时,CMV、CCV和THD3个智能压实间接指标的变异系数也随着压实遍数的增加而减小,因此定性上看,这3个指标都能表征黏土压实后越来越均匀的趋势。但是,3个智能压实间接指标的变异系数是传统压实度的10倍,两者基本相差了一个数量级,因此从均匀性的角度,单个智能压实间接指标表征土体压实的均匀性仍不太理想。
4 基于BP神经网络的压实度预测分析
4.1 模型的建立及预测
连续智能压实系统中对土体压实强度的判定是基于智能压实间接指标和传统压实度之间的相关性。BP神经网络是一种按照误差逆向传播算法训练的多层前馈神经网络,对多输入-单输出的映射关系具有较强的适用性。该文通过3层BP神经网络(3-5-1)建立传统压实度与CMV、CCV和THD之间的映射关系,如图4所示。
(1) 输入层:输入层采用3个智能压实间接指标:CMV、CCV、THD。该文用前7个样本点的3遍数据

图4 BP神经网络建立传统压实度和智能压实间接指标的映射关系
(共21个)作为训练的样本数据。
(2) 隐含层:隐含层含有5个单元数量。
(3) 输出层:用对应的21个传统压实度数据作为训练网络的输出层。
该文采用第8个样本的3遍压实数据作为验证数据。同时,为了与各指标线性模型的预测能力进行对比,由21个数据分别拟合的CMV、CCV和THD与传统压实度的线性模型如式(6)~(8)所示。
CMV:y=3.824 7x-302.97,R2=0.647 9
(6)
CCV:y=2.208 3x-167.38,R2=0.587 3
(7)
THD:y=0.328 7x-24.52,R2=0.538 2
(8)
最终得到的BP神经网络和3个线性模型的预测值如表2所示。从预测值与真实值的误差百分比来看,BP神经网络的误差最小,预测能力最强;相比CMV、CCV和THD单指标线性模型,BP神经网络的平均误差可分别下降55%、67%和58%。
4.2 模型预测结果的均匀性
采用上述训练好的3层BP神经网络(3-5-1)预估各样本的传统压实度值,并根据式(5)统计每遍的变异系数。最终,各指标在不同压实遍数下变异系数分布如图5所示。由图5可见,BP神经网络方法对应的变异系数介于传统压实度和单指标之间,变异系数都控制在0.1以下。图5表明采用BP神经网络联合CMV、CCV和THD3个指标进行压实度综合预测,更能贴近原来的传统压实度的均匀性,故BP神经网络模型适用性更强。
智能压实间接指标都是通过信号的畸变程度来侧面反映路基的压实状态,由于CMV、CCV和THD的侧重点不同,三者对不同土体的适应性也不一样。但是,这种经验类指标很难完全量化对各种土体的适应性,而通过BP神经网络隐式关系将这三者综合起来,将会增加预测土体压实度的准确性和鲁棒性。从预测路基压实的强度和均匀性上看,基于多指标的BP神经网络模型比单一指标更有效。该文数据量样本较少,24个样本量训练得到的BP神经网络模型在压实强度预测误差上能减少50%,变异系数能降低55%以上。在实际工程中,随着实测数据有效样本的增加,BP神经网络模型将得到更好的训练,输入层和输出层之间的隐式关系更为可靠。因此,在路基连续压实系统中,采用人工智能算法建立智能压实间接指标与传统压实指标的关系更为合理,工程适用性强。
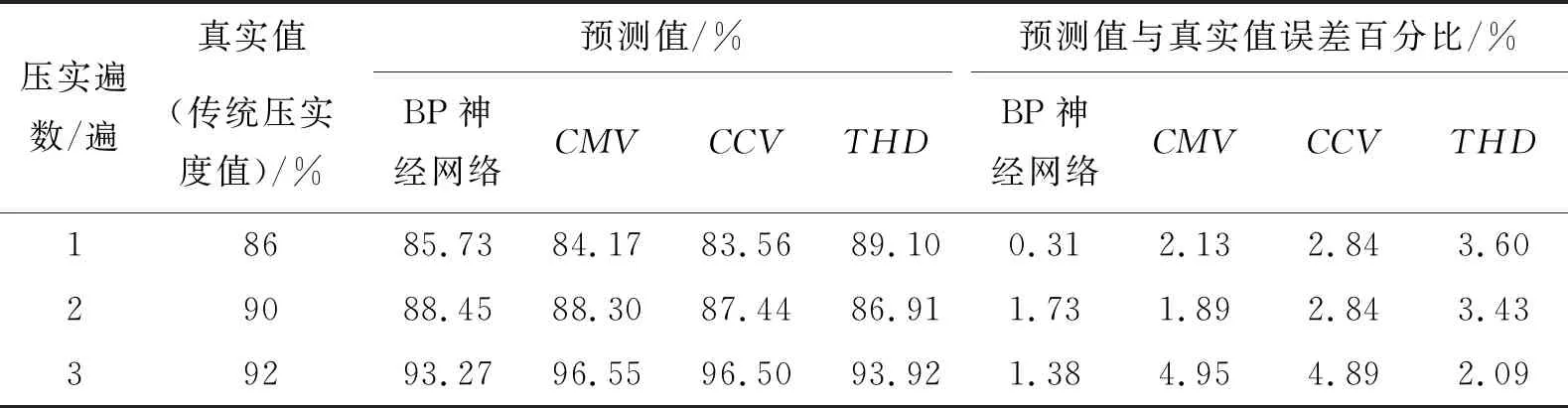
表2 BP神经网络和3个线性模型的预测值
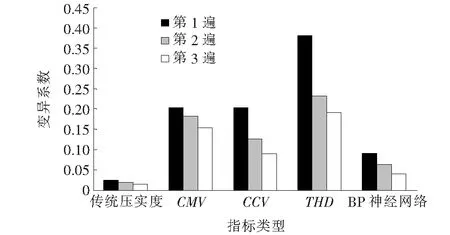
图5 不同压实遍数和不同指标变异性的分布
5 结论
(1) 分析了连续智能压实系统的组成,明确了压实强度和均匀性的判定是智能压实系统的重要内容,介绍了3种智能压实间接指标计算方法。
(2) 采用同一区域内智能压实指标的变异系数可描述压实的均匀性,施工中填筑路基土应进行多遍压实,但单个智能压实间接指标表征土体压实强度和均匀性的能力有限。
(3) 通过3层BP神经网络建立了传统压实度与CMV、CCV和THD之间的映射关系,验证了采用人工智能算法可有效提高智能压实间接指标的工程适应性。
