后张法预应力筋锚固损失计算的虚拟张拉法

2020-06-05伍彦斌黄方林

中外公路 2020年2期

伍彦斌，黄方林

(1.湖南方圆建筑工程设计有限公司，湖南长沙 410007；2.中南大学土木工程学院)

1 前言

后张法预应力混凝土结构中，锚固损失是预应力筋锚固瞬间由于锚具变形、钢束回缩和接缝压密等引起的一种瞬时预应力损失。锚固损失的计算，应考虑锚固瞬间钢束回缩过程中反向摩阻作用的影响。研究表明：当预应力筋与孔道之间的摩擦作用较大时，锚固损失主要集中在张拉端附近的局部范围内，张拉端锚固损失值可高达锚下张拉控制应力的20%～30%。因此，锚固损失将对结构的力学性能特别是锚固区附近的局部抗裂性能产生显著影响，锚固损失的准确计算非常重要。

近年来，不少学者对后张法预应力筋锚固损失的计算方法进行了研究。对于平面多段曲线且曲线段为圆弧的预应力筋锚固损失的计算，可采用分段解析法，通过分析钢束微段的平衡，利用变形协调条件及应力连续条件，导出预应力筋锚固损失的理论计算公式。对于线形复杂的空间曲线预应力筋，则一般采用基于正、反向摩阻对称性假设的数值方法进行计算，假设预应力筋锚固时的反向摩阻损失与张拉时的摩阻损失对称，对力筋各个定位点对应的有效应力图面积进行逐次试算，搜索满足变形协调条件的回缩终点位置，确定反向摩阻区段长度和锚固损失。

分段解析法计算结果精确，但计算分析难度大、过程复杂，主要适用于能够建立函数式的平面曲线且曲线段为圆弧的情况。实际中预应力筋的几何线形多种多样，对于既有竖弯又有平弯的空间曲线，很难采用解析法进行计算。而已有数值方法中正、反向摩阻损失的对称性假设，会过高地估计锚固损失值，与实际情况不符。

该文通过分析预应力筋锚固时发生回缩变形的原因，揭示回缩变形过程中“反向摩阻损失”的本质是由内部力筋内力对反向摩阻区段进行“反向张拉”而产生的摩阻损失，从而提出“虚拟张拉法”，编制适用于任意线形预应力筋锚固损失计算的非对称数值程序，并形成自定义宏命令，实现有限元模型中预应力筋有效预应力的批量计算。

2 虚拟张拉法的提出

2.1 基本原理

后张法预应力混凝土结构中预应力筋锚固前、后的伸长量变化如图1所示。设无应力长度为l的预应力筋AB在A端初始张拉时，总伸长变形量为Δl0；锚固瞬间的回缩变形量为Δlf；回缩终点为E，张拉端至回缩终点的范围为反向摩阻区段lf。

锚固瞬间预应力筋发生回缩变形的原因，是力筋存在有效内力。如图2所示，将预应力筋AB以回缩终点E为界分为AE、EB两个段落，张拉端A锚固瞬间，EB段力筋的内力分布及伸长量不变，力筋在E点处的有效内力PE也不变，而反向摩阻区段AE的摩阻力方向发生改变。受到力筋有效内力的“张拉”作用，AE段力筋的受力状态与在E点以初始有效内力PE进行反向张拉的情形相同。

图1 预应力筋伸长量示意图

图2 锚固瞬间状态变化示意图

将回缩终点E作为“虚拟张拉端”，将回缩终点E处的初始有效内力PE作为“虚拟张拉力”，对力筋反向摩阻区段AE进行虚拟张拉，则虚拟张拉完成后AE段力筋的受力状态，即为锚固损失完成后的受力状态；反向摩阻损失的本质，是内力“张拉”产生的正摩阻损失。

2.2 变形协调方程

由以上分析可知：回缩变形仅发生在AE段力筋范围内。根据锚固前后预应力筋伸长量的变化，虚拟张拉过程的变形协调方程为：

Δlf=ΔlAE-ΔlAE′

(1)

式中：ΔlAE为AE段真实张拉时的初始伸长量；ΔlAE′为AE段锚固后的实际伸长量，也即AE段力筋虚拟张拉的伸长量。

预应力筋的虚拟张拉(内力张拉)和真实张拉(外力张拉)满足相同的摩阻损失规律。在真实张拉端建立正坐标系，在虚拟张拉端建立反向坐标系，则预应力筋锚固前后的有效应力分布如图3所示。图中粗虚线为传统数值方法的有效应力曲线(对称)，σE为有效应力；s为从真实张拉端A起至计算位置处的空间曲线累计长度；s′为从虚拟张拉端E起至计算位置处的空间曲线累计长度；σcon为锚下张拉控制应力；σL2为锚固损失；σL1为真实张拉时的摩阻损失；σL1(E)为回缩终点E处真实张拉时的摩阻损失；σL1′为虚拟张拉时的摩阻损失；σE1(s)为真实张拉时扣除摩阻损失后的初始有效应力。

图3 有效应力分布

根据任意线形预应力筋摩阻损失理论，真实张拉时，AE段力筋的摩阻损失和伸长量分别为：

σL1=σcon[1-e-(μθ+ks)]

(2)

(3)

式中：θ为从真实张拉端A起至计算位置处的空间曲线包角；μ为力筋与孔道之间的摩擦系数；k为孔道偏差系数；Ep为预应力筋弹性模量；Ap为预应力筋截面面积；其余符号意义同前。

虚拟张拉时，“锚下控制应力”即虚拟张拉端的初始有效应力。AE段预应力筋的虚拟摩阻损失和虚拟伸长量分别为：

σL1′=σE1(E)[1-e-(μθ′+ks′)]

(4)

(5)

式中：σE1(E)为真实张拉锚固前E点的初始有效应力；θ′为从虚拟张拉端E起至计算位置处的空间曲线包角；其余符号意义同前。

将式(3)、(5)代入式(1)，变形协调方程为：

(6)

对于给定的预应力筋，可编制数值计算程序，采用逐次搜索的方法，求解式(6)中的lf。

当力筋长度较短，或锚固瞬间的回缩变形量较大时，回缩终点可能到达非张拉端。此时，反向摩阻区段lf为预应力筋全长，非张拉端也相应产生锚固损失，预应力筋的有效应力分布如图4所示。图中σL1(B)为锚固前非张拉端B的摩阻损失；σL2(B)为非张拉端B的锚固损失，即图中B、E两点的竖坐标之差；其余符号意义同前。

图4 lf为全长时的有效应力分布

对比左、右两端张拉的伸长量变化，变形协调方程为：

ΔlL-Δlf=λΔlR

(7)

(8)

式中：ΔlL为以初始张拉力P0左端张拉时的总伸长量；ΔlR为以初始张拉力P0右端张拉时的总伸长量；λ为张拉力折减系数；其余符号意义同前。

以非张拉端B点为虚拟张拉端，以折减后的张拉力λP0为虚拟张拉力，对力筋全长进行反向虚拟张拉计算，即得到锚固损失后的有效预应力分布。

3 虚拟张拉法的数值程序

实际预应力混凝土结构中，预应力筋数量繁多，且空间线形多样，为便于批量处理，该文基于常用有限元软件平台Ansys的参数化设计语言(APDL)，编制了预应力筋锚固损失计算的虚拟张拉法非对称数值程序，并形成“宏”命令。在宏命令中，共设置9个自定义参数(arg1～arg9)，实现参数输入、轴线方向识别、张拉方式控制、长度单位换算等功能，程序中所有的积分运算均采用梯形积分公式。单端张拉计算程序主要流程如图5所示，图中nn为预应力筋的总束数。

数值计算程序说明如下：

(1) 输入张拉控制应力σcon、弹性模量Ep、摩擦系数μ、孔道偏差系数k、回缩量Δlf等已知参数。

(2) 计算单端(左端)张拉时各个定位节点处扣除摩阻损失后的初始有效应力和初始伸长量，形成初始有效应力向量σE0和初始伸长量向量Δl0。

(3) 循环计算力筋在第j点(j=3～n，n为力筋ii的定位点总数)处以初始有效内力虚拟张拉时，第1～j点的虚拟有效应力、虚拟伸长量等数据，形成虚拟有效应力矩阵S和虚拟伸长量矩阵D：

(9)

(10)

式中：σjj为虚拟张拉端j点的初始有效应力；σij为反向摩阻区段内i点的虚拟有效应力；Δlij为反向摩阻区段内从j点起算至i点的累计虚拟伸长量；Δl1j为在j端虚拟张拉时的总虚拟伸长量；i=1～j。

图5 非对称数值计算程序框图

(4) 循环比较各个定位点处初始伸长量与虚拟伸长量的差值，当满足变形协调条件时，退出循环，得到回缩终点的精确位置，从而确定反向摩阻区段内的有效应力分布，最终得到预应力筋全长的有效预应力分布。

(5) 对于反向摩阻区段为全长的情况，则将右端张拉形成的有效应力乘以折减系数λ，即为左端张拉锚固损失后的有效预应力。

4 算例分析

为验证该文虚拟张拉法的正确性，选取经典算例——文献[6-8]中的小凌河特大桥32 m预应力混凝土简支箱梁N4、N6钢束和文献[6]中的老万福河大桥腹板下弯束N4(为便于区分，该文重新编号为N4a)进行锚固损失计算，3束预应力筋的竖弯曲线如图6所示。

图6 算例竖弯曲线(单位：cm)

N4a钢束在A端张拉，弹性模量Ep=195 GPa，张拉端锚下控制应力为σcon=1 395 MPa，力筋回缩变形值Δlf=6 mm，摩擦系数μ=0.23，孔道偏差系数k=0.001 5；N4、N6钢束在A端张拉，弹性模量Ep=195 GPa，张拉端锚下控制应力为σcon=1 250 MPa，力筋回缩变形值Δlf=6.8 mm，摩擦系数μ=0.265，孔道偏差系数k=0.003。

以上3束预应力筋的弯起角各不相同，均为典型的5段式(对称)桥梁结构预应力筋，且曲线段为圆弧，可采用分段解析法计算。分别采用分段解析法、基于正、反向摩阻对称性假设的数值方法(以下简称“对称方法”)和该文提出的虚拟张拉法进行预应力筋锚固损失计算。数值计算中，力筋定位点划分间距为10 mm，计算公式中的力筋累计长度均采用空间曲线长度。

算例中3束预应力筋的主要计算结果见表1。表中lf为反向摩阻区段长度，为空间曲线长度(文献值已换算)；σL2(A)为张拉端的锚固损失；σL2(B)、σL2(C)分别为预应力筋圆弧段起、止点处的锚固损失；相对差1、2分别为对称方法、该文虚拟张拉法计算值与解析解的相对误差。

表1 预应力筋的计算结果

从表1可以看出：

(1) 采用该文虚拟张拉法计算得到的预应力筋反向摩阻区段长度和预应力筋沿程锚固损失与解析解高度吻合，反向摩阻区段长度计算值的最大相对误差仅为0.19%，张拉端锚固损失计算值的最大相对误差仅为0.17%，该文虚拟张拉法可实现预应力筋锚固损失的准确计算。

(2) 采用对称方法则存在较大的误差，其计算所得的反向摩阻区段长度小于解析解，张拉端锚固损失大于解析解，且计算误差受预应力筋线形的影响较大。预应力筋的弯起角越大，则锚固损失越大，采用对称方法的计算误差也越大。当回缩终点位于圆弧段与平直段的临界位置时，锚固损失值相对误差为100%；其他情况下最大相对误差约为35.8%。

采用对称方法和虚拟张拉法计算得到3束预应力筋锚固损失前、后的有效应力分布如图7所示。

从图7可以看出：有效应力的分布曲线与线形相对应，不同线形导致3束预应力筋的回缩终点位于不同位置。对于弯起角最小、曲线段长度最短的N4a钢束，当回缩变形量为6 mm时，回缩终点位于圆弧段，采用对称方法的计算误差最小；对于弯起角较大、曲线段长度较长的N4钢束，当回缩变形量为6.8 mm时，回缩终点位于圆弧段与平直段的临界位置，采用对称方法的计算误差较大；对于弯起角最大、曲线段长度最长且曲线半径最小的N6钢束，当回缩变形量为6.8 mm时，回缩终点位于力筋中部平直段，采用对称方法的计算误差最大。

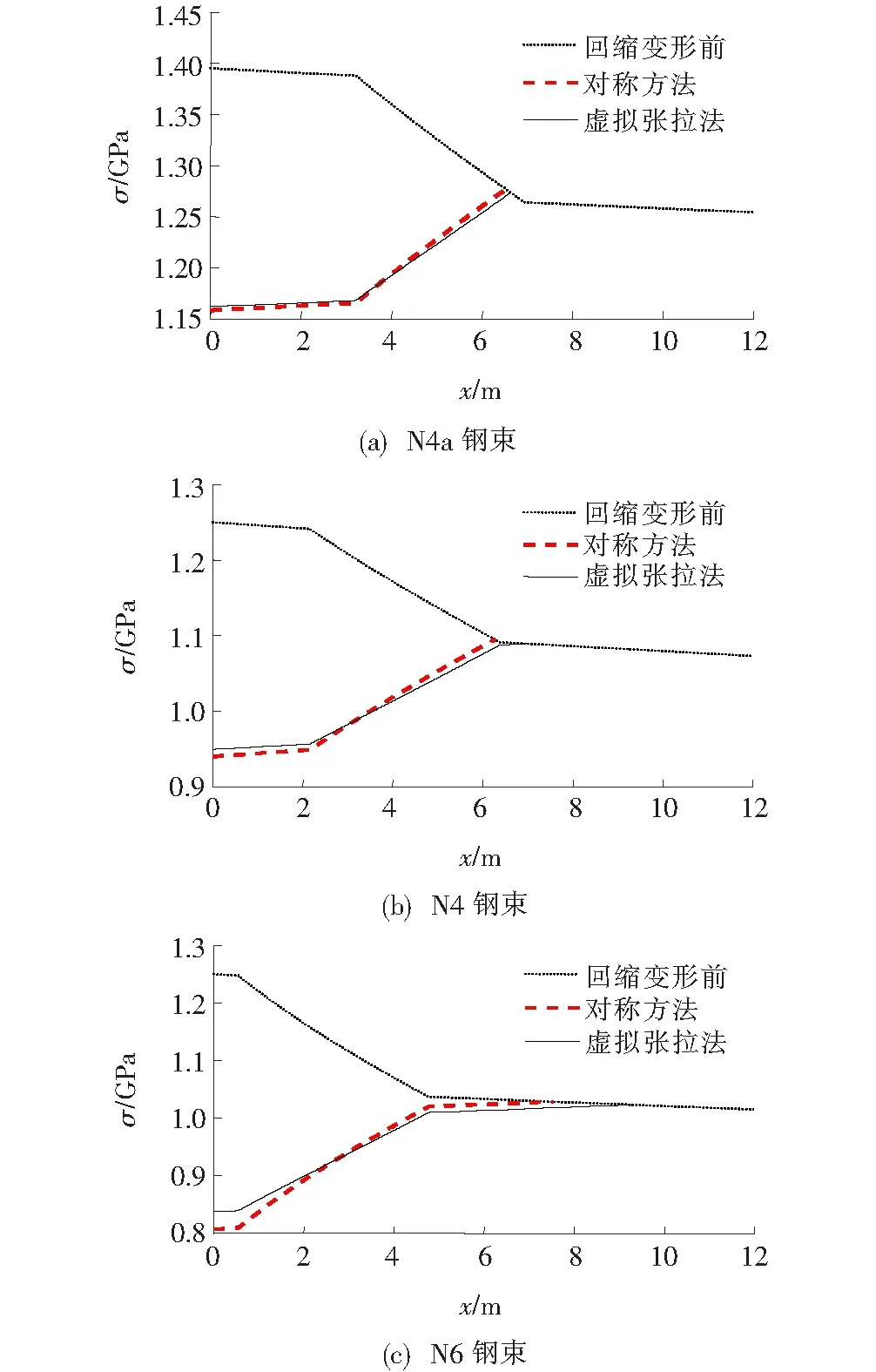
图7 钢束有效应力分布曲线

由此可见，采用对称方法，其计算误差的大小受预应力筋线形和回缩终点位置的影响，当力筋弯起角较大，或当回缩终点位于力筋中部平直段内时，计算误差也相对较大。

为了进一步考察对称方法计算误差的分布规律，仍以N4a钢束为例(假设其在长度对称中心位置锚固)，计算回缩变形量为1～12 mm的锚固损失。采用对称方法和虚拟张拉法计算得到的锚固损失比例σL2(A)/σcon、反向摩阻长度比例lf/l随回缩变形量的变化如图8、9所示。

从图8、9可以看出：① 当回缩变形量为1～12 mm时，预应力筋锚固损失占锚下张拉控制应力的比例可达5%～25%，与回缩变形量呈非线性关系；② 当回缩变形量为1～6 mm时，反向摩阻区段为部分力筋长度，两种方法的锚固损失计算结果非常接近；③ 当回缩变形量为7～9 mm时，反向摩阻区段长度突然增大，分析可知：此时回缩终点恰好位于曲线段与平直段的临界位置附近，两种方法的锚固损失计算结果偏差也较大；④ 当回缩变形量为9～12 mm时，lf为力筋全长，经计算，张拉端锚固损失的相对误差约为5%。