实测与规范风谱下某悬索桥抖振响应定性比较

汪磊，张志田，谭卜豪，马健，袁少洋

(1．云南省交通规划设计研究院，云南 昆明 650011；2.湖南大学 土木工程学院)

桥梁等结构在随机风荷载作用下的随机响应即抖振。是否能准确分析一座桥梁的抖振响应由3个环节来控制。① 结构本身的描述，包括有限元模型中质量、刚度、几何以及材料非线性、边界条件；② 结构气动力特性的描述，包括主要受风构件的静风力特性、气动导纳特性以及自激力特性。根据静风力系数以及气动导纳特性可建立从脉动风至随机气动力的转换关系。根据自激力特性则可考虑结构的振动对气动自激力的反馈修正作用，这一作用在频域内表现为气动阻尼与气动刚度的形式；③ 来流风特性的描述，包括脉动风的自功率谱、互谱以及相关谱特性。从工程实际看，这3个环节中最易把握的是对结构的描述；对气动力特性的描述通常采用风洞试验的方法解决，实际应用中可视情况进行简化，如不考虑气动导纳或采用简化的气动导纳函数，在假设流固耦合效应不明显时也可忽略自激力特性；相比之下，最难准确把握的是输入特性，即脉动风的谱特性。湍流特性对抖振影响很大。当输入特性脱离实际情况时，结构特性以及气动力特性描述得再准确也无济于事，得到的结果完全有可能与工程实际情况大相径庭，对于山区复杂地形这一问题可能更加突出。JTG/T D60-01-2004《公路桥梁抗风设计规范》将风场分成4类，根据建议的水平及竖向风谱公式结合4类风场指定的风参数可得到具体的风谱值。该文结合某一山区大跨桥梁桥址现场实测脉动风特性进行抖振响应分析，并与基于规范建议谱的结果进行对比。

1 现场风特性

现场风特性采用30 m高的塔布置两层风观测仪进行观测。两层风观测仪分别位于10 m及30 m高度处。

现场测得的典型瞬时风速时程如图1所示。实际观测到的风速在长时间范围内(以d为单位)具有较明显的非平稳特征，但对于给定的一座桥梁，用于结构设计的风速以及内力值却是固定的，如100年一遇、10 min时距下与桥址相应的风场产生的各类设计值。该文在为期1年多的观测数据中，提取20 min时距内平均风向平稳(分布在283°～289°之间，该方向大致与桥轴线垂直)的若干条时程进行处理，得到顺风向与竖向的脉动风时程，进而进行谱分析得到每个样本的风谱，最后将所有样本的风谱按频率点进行平均后得到该风速段与该风向的实测平均风谱(图2、3)。考虑到风谱对风速值的依赖性，首先选择合理的风速值。给定风速值下，20 min时距的样本须具有足够的风向以及风速平稳性。如图1所示，显然风速越小可得到的样本越多，越高则样本数越少。结合实际观测结果，在10～12 m/s的风速范围内选取满足方向与平稳性的样本。

图1 实测30 m高度处瞬时风速时程(2017年)

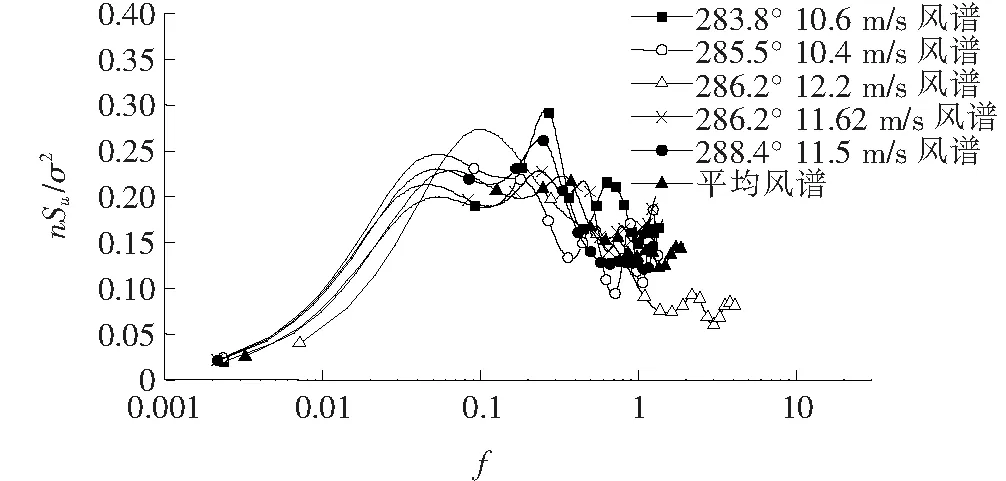
图2 实测顺风向脉动风谱

图3 实测竖向脉动风谱

山区峡谷中的风场具有空间分布特性，即空间不同点具有不同的谱特性。实际工程中要得到每一点的谱特性进行输入是不可行的。该文仅通过观测位置的谱特性入手进行研究，目标不是准确描述山谷中桥梁的随机风荷载分布，而是定性地讨论实测与规范风谱下可能造成的差异。

JTG/T D60-01-2004《公路桥梁抗风设计规范》建议顺风向风谱采用Kaimal谱，其表达式如下：

(1)

(2)

(3)

式中：u*为流动剪切速度；S1u(z,n)为顺风向Kaimal谱(m2/s)；Z为距地面高度；n为脉动风频率(Hz);f为莫宁坐标系无量纲频率；U为平均风速；σu为顺风向脉动风均方差。规范建议采用Panofsky谱拟合竖向风谱，如式(4)所示：

(4)

式中：S3w(z,n)为竖向风谱。

该文将分别采用基于实测的风谱以及规范建议的风谱进行抖振分析与对比。为保证对比的合理性，遵循以下两条原则：① 桥面高度处的平均风速值一致，均为11.2 m/s；② 脉动风的相关谱一致，由于相关谱缺少现场实测，全部统一采用以下公式：

(5)

式(5)中衰减指数的计算为：

(6)

式中：n为频率；z1、z2为两点的水平坐标；y1、y2为两点的竖向坐标；Cz、Cy为控制两点水平及竖向相关性的相关系数。

2 有限元模型及抖振频域算法

拟建桥梁为一超大跨度悬索桥，主跨920 m，采用混凝土桥塔与钢箱加劲梁。采用单主梁法建模，有限元模型如图4所示。全桥共464个节点，626个单元。桥塔与加劲梁采用不考虑剪切变形的欧拉-伯努力三维梁单元模拟；主缆与吊杆采用杆单元模拟。模型中坐标轴x、y、z分别为顺桥向、竖向以及侧向。

图4 抖振分析有限元模型

加劲梁断面的三分力系数如图5所示。采用频域多模态耦合方法进行抖振分析，这一基本方法在国内外已经得到广泛应用。该文采用Visual C++实现数值算法，以下给出基于节点与单元的频域抖振有限元求解的离散格式。

在不考虑气动导纳修正并假设脉动风速远小于平

图5 加劲梁静风荷载三分力系数

均风速值的情况下，可采用以下Davenport表达式来描述加劲梁断面每延米的抖振力：

(7a)

(7b)

(7c)

式中：Db、Lb、Mb分别为每延米的抖振阻力、升力以及升力矩关于时间t的函数；u(t)、w(t)分别为顺风向、竖向脉动风时程；U为平均风速；CD、CL、CM分别为阻力、升力、升力矩系数，为风攻角α的函数；B为参考宽度；ρ为空气密度；CD′=dCD/dα、CL′=dCL/dα、CM′=dCM/dα分别为阻力、升力系数、升力矩系数对风攻角α的导数。

当平均风速固定时，单元节点上所分配到的抖振力可表示为脉动风的线性函数，如下所示：

Db(t)=Δx[αDu(t)+βDw(t)]

(8a)

Lb(t)=Δx[αLu(t)+βLw(t)]

(8b)

Mb(t)=Δx[αMu(t)+βMw(t)]

(8c)

式中:Δx为分到该节点的有效长度；αi、βi(i=D,L,M)为常数，可通过比较式(7)、(8)得出。

采用振型分解法对结构进行抖振求解，其第i阶模态的广义运动方程为：

(9)

式中：Ii为第i阶模态的广义质量；ξi、ζi、ωi分别为第i阶模态的广义运动坐标、阻尼比以及自然频率；Qbi为第i阶模态力。

假设结构上需要考虑抖振力的节点共有k个，每个节点上均作用有气动阻力、升力与升力矩，则模态力可表示为：

(10)

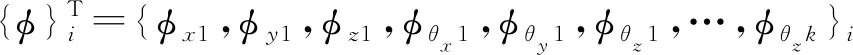
(11)

由于只考虑升力、阻力与升力矩，因此每一个节点的6个力矢量只有3个分量不为0，最后抖振力向量表达为：

{F}b={0,Lb1,Db1,Mb1,0,0,…,Mbk,0,0}

(12)

n阶模态参与分析的矩阵运动方程为：

(13)

式中： {ξ}、{q}分别为模态运动坐标向量、广义模态力向量，其表达式分别为：

(14)

(15)

式中：Ii为第i阶模态的模态质量。[I]、[C]、[K]均为n×n阶矩阵，其表达式分别如下：

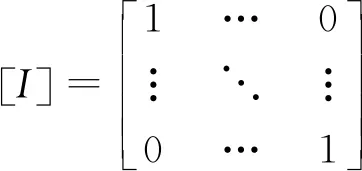
(16)

(17)

(18)

定义形如下式所示的Fourier变换：

(19)

对式(13)进行如式(19)所示的Fourier变换后可得：

(20)

式中：

[E]=-ω2[I]+iω[C]+[K]

(21)

将式(20)两边求共轭后再与式(20)本身相乘可得

[E][Sεξ][E]*=[SQbQb]

(22)

变形后可得：

[Sξξ]=[E]-1[SQbQb][E]*-1

(23)

式中：[Sξξ]为n×n阶广义模态坐标的功率谱密度矩阵，其表达式如下：

(24)

(25)

由于加劲梁上只考虑抖振阻力、升力以及升力矩，因而式(25)中第i阶模态的模态抖振力频谱为：

(26)

在式(26)的基础上，可得到模态荷载功率谱密度矩阵任意元素的表达式如下：

(27)

式(27)括号中共由9项组成，每一项可继续展开，以第1项为例，可展开得到：

(28)

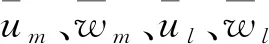
最后，根据频谱与功率谱的关系，式(28)可写成如下风谱的形式：

(29)

式中：Suu(xm,xl)、Suw(xm,xl)、Sww(xm,xl)分别为m与l两位置处顺风向脉动风相关谱、顺风向脉动风与竖向脉动风交叉谱、以及竖向脉动风相关谱。

从式(29)、(27)到式(23)的逆运算过程建立了从空间不同点脉动风速相关谱以及交叉谱转变到结构模态坐标运动功率谱密度矩阵的计算过程。

最后，结构任意两点6个自由度方向位移的功率互谱密度函数可按以下公式计算：

(30)

(31)

(32)

(33)

(34)

(35)

对功率谱进行积分可得位移的方差函数，以竖向响应方差为例，其积分表达式如下：

(36)

当xm=xl时，即可得某一点的位移响应方差。有了节点位移响应的均方差后，最后根据单元刚度矩阵可得节点的抖振内力响应均方差，具体过程不再详述。实际求解过程中，并非采用式(36)的积分表达式，而是从圆频率ω=0开始，选择一个合理的积分上限，以某一足够精细的扫频增量Δω进行离散求解，为提高数值求解效率，可采用变增量扫频算法大幅缩短求解时间，具体过程可参考文献[10]。

3 频域抖振结果

该文用Visual C++语言实现以上频域抖振求解过程，并应用于风观测现场拟建的桥梁。抖振求解选取前40阶模态参与；采用瑞利阻尼模型并控制第1阶竖弯与第1阶扭转模态阻尼比为0.4%，其他模态阻尼比按阻尼模型自动计算；初始扫频增量设为0.001 rad/s，扫频截断频率为3.2 rad/s，基本覆盖了参振的所有模态。按照现场实测的风速样本，当采用规范建议的风谱计算时，桥面高度处的平均风速控制在11.2 m/s。为进行全面比较，针对规范中所有4类场地进行了抖振分析。

图6～8分别给出了加劲梁的竖向、侧向以及扭转响应均方差分布。

图6 主梁竖向响应均方差分布

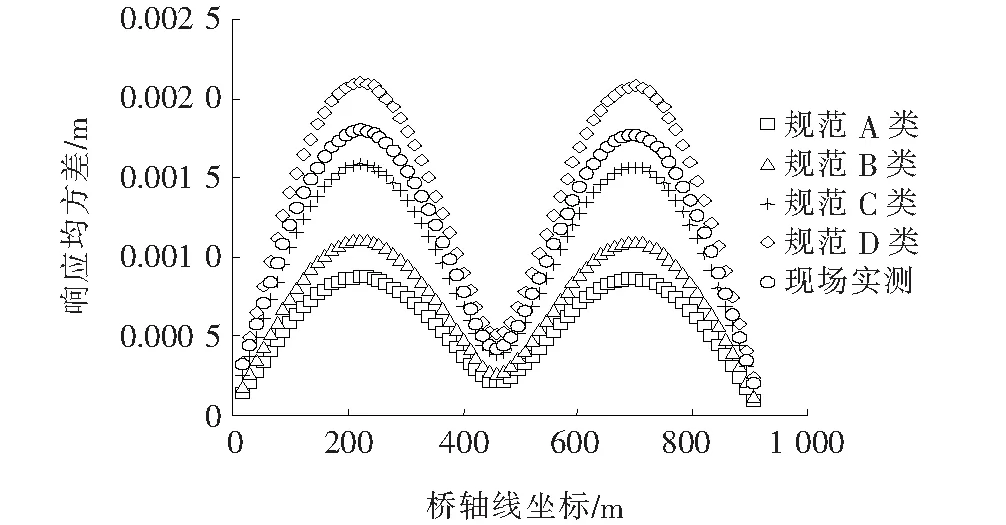
图7 主梁侧向响应均方差分布

由图6～8可知：

(1) 基于规范建议风谱的抖振响应，从A类场地到D类场地逐渐增大，D类场地的响应约为A类场地响应的2.5倍；整体来看，基于现场实测风谱的抖振结果位于规范C类与D类场地之间。对于竖向响应，基于实测谱的响应已经很接近规范D类风场结果，对于侧向与扭转，基于实测谱的响应基本位于规范C类与D类结果中间。

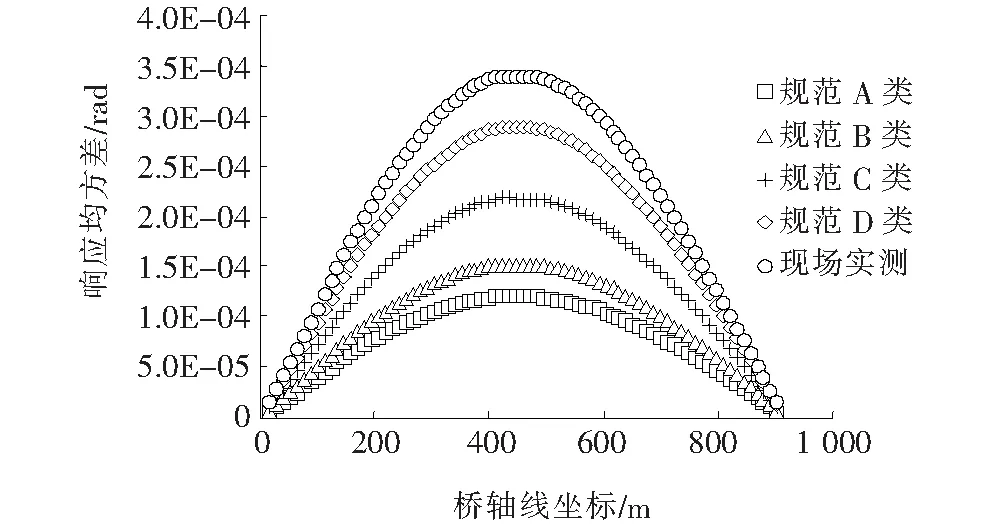
图8 主梁扭转响应均方差分布

(2) 竖向响应在桥跨中间数值较大(正对称竖弯模态贡献)，在两侧四分点有突出分布(反对称竖弯模态贡献)，因此对称与反对称竖弯模态均明显参与抖振响应；侧向响应的分布曲线在跨中数值很小，两个四分点形成突出的峰值，因此主要参振模态为反对称模态；扭转响应分布曲线很对称单一，可以判断主要由正对称扭转振型参与。

图9、10分别给出了加劲梁左侧四分点的竖向响应功率谱曲线、跨中扭转响应的功率谱曲线。

图9 主梁竖向位移响应功率谱

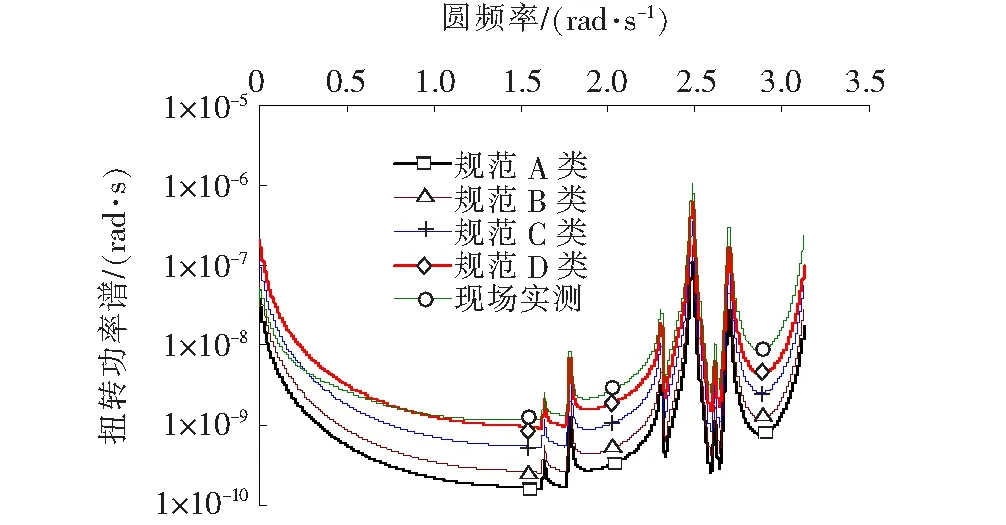
图10 主梁扭转位移响应功率谱

从图9、10可知：竖向响应参与的模态较多，是典型的多模态耦合抖振响应；由于扭转频率较高，因此在圆频率2.0 rad/s之前基本上只有背景响应，在2.0～3.0 rad/s之间有几阶模态有明显的共振响应。

比较图10、11中基于现场实测曲线与规范D类曲线可知：在高频区，基于现场实测的响应功率谱均在基于规范D类的功率谱曲线之上；而在低频区，现场实测曲线在规范D类之下，在更低的频率范围内甚至位于规范C类之下。这一特征与前面的均方差分布曲线有明显的不同，也间接说明规范建议的风谱在高频区的能量低于现场实测风谱，在低频区的能量则高于现场实测风谱。

图11给出了左右桥塔单柱根部3个方向抖振力的均方差；图12则给出了相应部位3个方向抖振力矩均方差。由图11、12可知：塔高形成抖振内力的差异十分明显，远高于塔高本身之间的差距。以力矩Mx的均方差为例，左塔柱底部为13 067 kN·m，而右塔柱底部为5 667 kN·m，前者为后者的2.3倍。

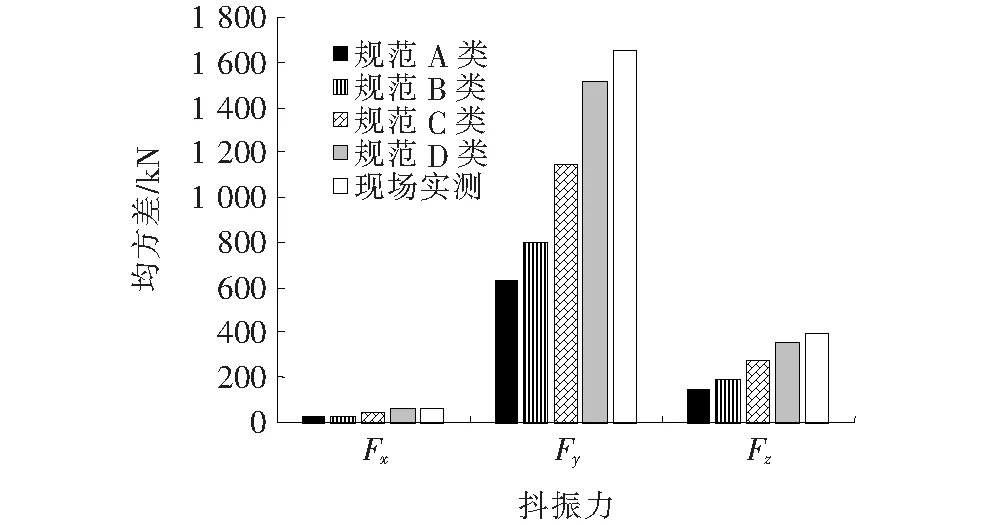
(a) 左桥塔柱根部

(b) 右桥塔柱根部

与加劲梁位移响应形成鲜明对比的是，基于现场实测风谱得到的塔基抖振内力明显高于所有4类基于规范谱的结果。目前，形成这一现象的机理并不十分明确，但结合前面给出的响应功率谱曲线来看，应当与桥塔本身频响特性有关。相对主体结构而言，桥塔本身的共振区间分布在高频区，在高频区间现场实测的风谱高于4类规范建议谱。

4 结论

该文基于桥址实测风谱以及规范建议风谱对拟建主跨约1 000 m的悬索桥进行了频域抖振分析，通过对计算结果的对比分析可知，基于JTG/T D60-01-2004《公路桥梁抗风设计规范》建议风谱进行桥梁抖振分析时，对位移与内力这两项指标可能得到相反的结果。因此对于十分重视抖振内力的桥梁，建议基于现场长期实测的风特性进行分析。具体结论如下：

(1) 从加劲梁位移抖振响应来看，基于现场观测风谱的响应值介于基于规范建议风谱的C类与D类场地结果之间，因此采用基于D类场地的规范建议谱计算加劲梁的抖振位移比较合理。

(a) 左桥塔柱根部

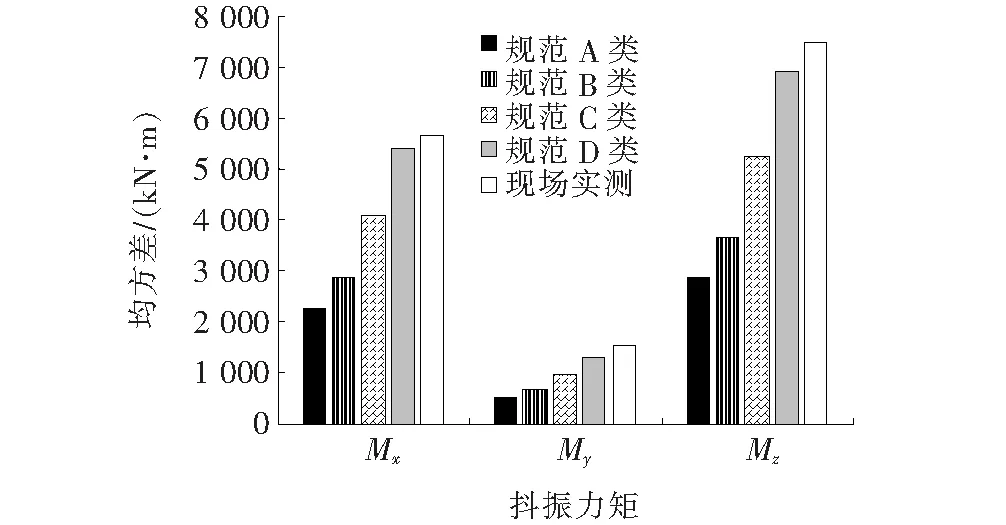
(b) 右桥塔柱根部

(2) 从塔基抖振内力结果来看，基于现场观测风谱的响应值高于基于规范建议风谱的所有4类场地的结果，因此即使采用响应值最大的D类场地规范建议谱进行分析，得到的抖振内力仍然偏于不安全。

(3) 从功率谱曲线来看，在低频处，基于现场实测谱的响应低于基于D类甚至C类场地规范谱的结果；而在高频处，基于现场实测谱的响应高于所有4类场地的规范建议谱的结果。