改进的无单元Galerkin方法在沥青路面动态响应中的应用

2020-06-05彭妙娟付杨

中外公路 2020年2期

彭妙娟, 付杨

(上海大学土木工程系，上海市 200444)

无网格方法是近年来快速发展的数值方法，由于该类方法的计算基于节点而非网格，因而在对大变形、断裂、爆炸等问题进行研究时具有一定优势，现在已成为计算力学领域的研究热点。

无网格方法主要有无单元Galerkin方法、无网格局部法、径向基函数法、自然单元法，其中无单元Galerkin( Element-Free Galerkin，EFG)方法是使用最普遍的无网格方法之一，EFG方法采用移动最小二乘法建立逼近函数，但计算量相比有限元较大。程玉民等基于移动最小二乘法，提出了改进的移动最小二乘法，并以此为基础，建立了改进的无单元Galerkin(Improved Element-Free Galerkin，IEFG)方法，并将其应用到势问题、瞬态热传导、波动方程、弹性力学和弹性动力学、断裂力学、黏弹性力学，由于改进的移动最小二乘法形成的方程组易于求解且不会形成病态方程组，因而 IEFG 方法比EFG 方法具有更高的计算精度和计算效率。

姚莉莉等基于变分原理，将温度荷载与车辆荷载进行耦合，并利用无网格方法计算分析了路面结构的温度场和应力场；李荣鑫等利用EFG方法模拟了沥青路面的力学行为，对沥青路面的车辙进行了分析；彭妙娟，席伟成等利用IEFG方法，通过设置不同的节点数量和影响域比例参数，对机场复合道面的位移和应力进行了分析；邹诗莹等将断裂力学和IEFG方法结合，分析了机场复合道面的反射裂缝。

目前，国内外在求解沥青路面动力响应时，使用有限元方法较多，而将无网格方法应用到路面动力响应的相关研究还较少。因此使用改进的无单元Galerkin方法对沥青路面动态响应的研究非常必要。

该文建立三维沥青混凝土路面分析模型，基于三维弹性动力学问题的IEFG方法对沥青路面结构的动力响应进行计算，并对路面结构不同深度的动力响应及位移进行分析。

1 改进的移动最小二乘法

在改进的移动最小二乘法中，逼近函数uh(x)的形式为：

(1)

式中：m为基函数个数；p(x)=[p1(x),p2(x),…,pm(x)]为基函数；ai(x)为相应的系数。

在点x邻域内的局部逼近函数为：

(2)

定义泛函：

(3)

式中：xI为点紧支域内的节点；w(x-xi)为权函数;n为影响域覆盖点x的节点数。

将式(3)用矩阵形式表示：

J=(Pa-u)TW(x)(Pa-u)

(4)

uT=(u1,u2,…,un)

(5)

(6)

W(x)=

(7)

为使误差最小，对J求一阶导数，从而得到系数向量：

A(x)a(x)=B(x)u

(8)

其中：

A(x)=PTW(x)P

(9)

B(x)=PTW(x)

(10)

利用Schmidt正交化方法将基函数正交化，例如对基函数：

(11)

正交化后的正交基函数为：

(12)

为加权的正交基函数组：

(pi,pj)=0，(i≠j)

(13)

由式(8)～(13)可得：

a(x)=A*(x)B(x)u

(14)

其中：

(15)

将式(14)代入式(1)，可得：

(16)

(17)

2 三维弹性动力学的改进的无单元Galerkin方法

三维线弹性动力学的控制方程为：

(18)

(19)

σ=[σ11,σ22,σ33,σ12,σ13,σ23]T

(20)

b=[b1(t),b2(t),b3(t)]T

(21)

u=[u1(t),u2(t),u3(t)]T

(22)

(23)

(24)

边界条件为：

(25)

(26)

初始条件为：

u(x,t0)=u0(x)，(x∈Ω)

(27)

(28)

式中：u0为点x的初始位移；v0为点x的初始速度向量。

采用罚函数法施加位移边界条件，可得弹性动力学的Galerkin积分弱形式：

(29)

式中：α为罚因子。

由弹性问题的几何方程和本构方程，代入改进的移动最小二乘法的逼近函数式(1)，可得：

(30)

其中：

(31)

(32)

(33)

(34)

(35)

(36)

(37)

(38)

(39)

(40)

若x1、x2或x3方向有位移约束，对应的S1、S2或S3为1，否则为0。

(41)

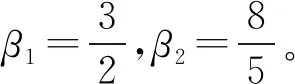
(42)

阻尼矩阵采用瑞利阻尼：C=αM+βM，其中α、β为阻尼系数。

3 三维动力学IEFG方法在沥青路面动态响应中的应用

该文利用Matlab编制了无网格法程序，建立了4层结构的路面分析模型，基于三维弹性动力学IEFG方法对移动荷载作用下的路面动态响应进行了计算，具体计算流程为：

(1) 确定路面几何尺寸，输入路面材料参数。

(2) 在求解域内确定坐标系，设置节点坐标，对应编号建立节点信息。

(3) 形成用于数值积分的背景积分网格，并建立Γu和Γt的边界积分网格信息。

(4) 根据背景网格和边界生成Gauss积分点并计算对应Gauss点积分信息。

(5) 形成刚度矩阵K，质量矩阵M，阻尼矩阵C，全局罚函数矩阵Ka及列向量Fα。

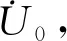
(8) 进入时间步循环，计算时间t+Δt的节点荷载向量Ft+Δt。

(9) 求解并输出路面各层计算点的位移、速度、应变和应力。

(10) 返回步骤(6)，计算Δt内车轮移动距离，确定新的荷载位置。

3.1 路面结构和参数

该文采用中国典型的半刚性沥青路面结构，路面结构及其各层材料参数见表1。

表1 沥青路面结构和参数

3.2 计算模型

沥青路面计算模型尺寸为：路面宽度方向3.75 m，长度方向8.68 m，厚度方向3.78 m。图1为路面模型节点分布，总节点数为2 304个；共1 736个积分子域，各个子域均采用3×3阶Gauss积分，取影响域比例参数dmax=2，罚因子为1×1010。为提高计算精度，采用局部细化的方式划分网格，在荷载作用区附近细化。

图1 路面模型节点分布

3.3 匀速移动荷载的模拟

图2为移动荷载加载过程，其中，黑色部分为等效荷载，箭头为荷载移动方向。将荷载的运动路径简化为水平表面上的两条矩形条带，荷载大小取0.7 MPa，作用面积简化为两个0.186 m×0.28 m的矩形，轮隙带取0.128 m，设计车速V=100 km/h，通过调节荷载的作用时间来模拟不同的车速，为减小边界条件对结果的影响，移动荷载加载过程如图2所示。

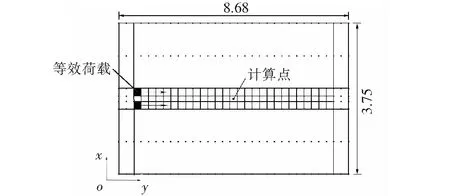
图2 移动荷载加载过程(单位：m)

4 三维沥青路面动态响应计算结果与分析

选取路面结构中心线上的各点作为计算点，利用弹性动力学IEFG方法进行计算，得到计算点在移动荷载作用下的竖向位移，并将其与有限元软件Abaqus的计算结果进行对比，沥青路面面层顶部计算点在移动荷载下的竖向位移比较见图3。

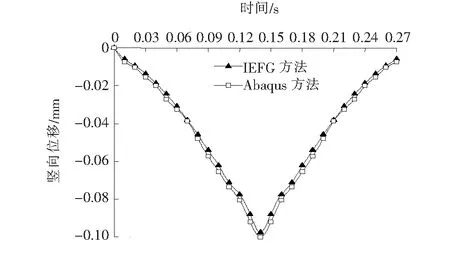
图3 面层顶部竖向位移比较

从图3可知：IEFG弹性动力学方法的计算结果与有限元Abaqus计算结果吻合，说明了IEFG动力学方法在分析沥青路面动态响应方面的有效性。

4.1 沥青路面结构层竖向位移分析

图4为沥青路面垂直方向各层计算点位置的竖向位移时程曲线。

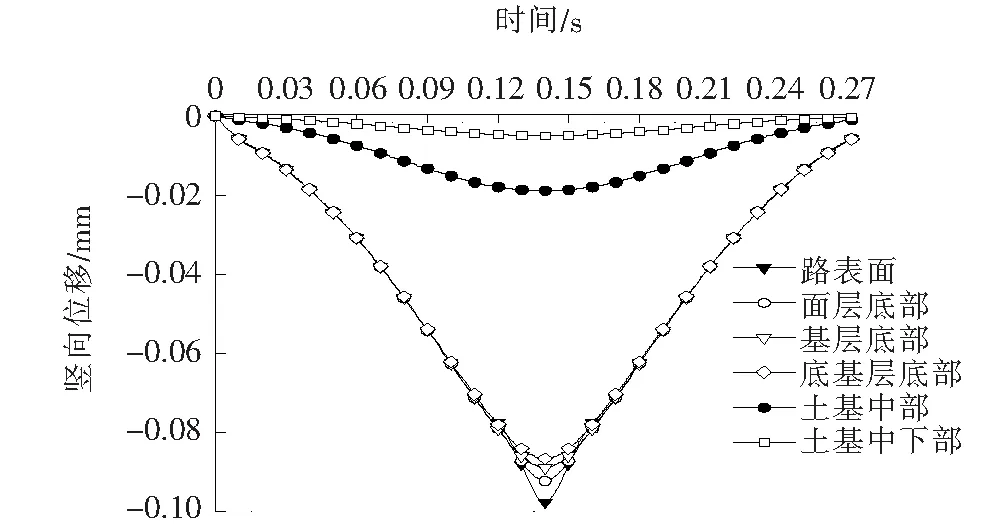
图4 各层竖向位移时程曲线

从图4可以看出：当荷载向计算点方向移动时，计算点的竖向位移快速增大，荷载在驶离计算点时，计算点位置各个深度的竖向位移迅速减少。在路面结构各层计算点的时程曲线中，竖向最大位移发生在沥青面层，为0.097 5 mm，基层底部、底基层底部的竖向位移分别占沥青面层位移的95.7%和93.2%；土基层顶部、中部分别占沥青面层位移的93.2%和26.9%。由以上分析可知：随着深度的增大，竖向位移值不断减小，竖向位移主要发生在土基中部以上。

4.2 沥青路面结构层应力响应分析

图5为路面结构计算点在移动荷载作用下的竖向应力、横向应力和水平应力时程曲线。图6为最大剪应力时程曲线。

由图5可以看出：

图5 沥青路面结构层应力响应时程曲线

(1) 在各计算点位的竖向应力时程曲线中，路表面承受最大压应力，大小为0.38 MPa；面层底部应力为0.17 MPa；在底基层底部计算点位置，压应力值为0.08 MPa；随着深度增加，土基中的应力值逐渐趋近于零。由以上分析可知：随着深度的增大，竖向应力减小，路面表面层承受了较大的压应力，易产生破坏。

(2) 路面结构的横向应力时程曲线和水平应力时程曲线的变化趋势基本一致，其中拉应力和压应力都有，并随深度增加呈交替变化。两个方向的最大压应力均出现在路表面，大小分别为0.27、0.30 MPa；随着深度的增加，两个方向的压应力均在面层快速减小，并在基层中由压应力转化为拉应力，两个方向最大拉应力均发生在基层和底基层的接触面，其值分别为0.19、0.23 MPa，从基层底部到土基中部，随深度的增加，两个方向的拉应力均逐渐减小，且在底基层的中上部，拉应力减小幅度最大，土基顶面拉应力值均为0.05 MPa。通过以上分析可得：在匀速荷载作用下，路面结构受力最为不利的位置分别为沥青面层表面和基层底部。