Hilbert K-模上框架的框架变换和正交投影

董芳芳

（天水师范学院 数学与统计学院，甘肃 天水 741001）

1 预备知识

HilbertC∗-模和Hilbert空间的主要不同在于：HilbertC∗-模不一定可补，并且HilbertC∗-模不一定有标准正交基，因此，M.Frank和D.R.Lar⁃son将HilbertC∗-模膨胀到：

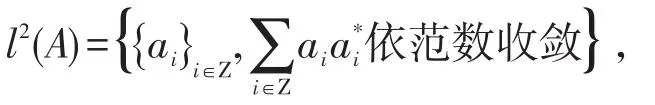
同时在l2(A)上定义模和内积：对 ∀a∈A和∀{ai},{bi}∈l2(A),

这样l2(A)就为HilbertC∗-模，它有双边的平凡的标准正交基：{em}m∈Ζ，{em}={0,…,0,1,0…}，在m位置为1，在其他位置为0，其中1为A中的单位元，然后在HilbertC∗-模到l2(A)上定义算子θ:H→l2(A)，使得对 ∀x∈H，，其中{xi,i∈J}为H的框架，{ei,i∈J}为l2(A)的标准正交基，并将θ定义为框架{xi,i∈J}的框架变换（见[1]）.

Hilbert K-模是一种紧算子代数模，也是特殊的HilbertC∗-模，其中底代数K为作用在Hilbert空间上的全体紧算子组成的C∗-代数，显然I∉K，因此，这种模无法膨胀，也就是说引入l2(K)毫无意义，D.Bakic和B.Guljas在文献[2]中证明了Hilbert K-模一定有特殊的标准正交基，其特殊点在于相同基向量的内积为K中的一个秩为1的自伴投影（见定义1.2），因此，本文直接在Hilbert K-模M本身上引入了广义框架的框架变换（见定义1.4）.

定义1.1[2]设K为作用在Hilbert空间Η上的全体紧算子组成的C∗-代数，Μ是复数域C上的线性空间，Μ 是左K-模，满足：μ(kx)=(μk)x=k(μx)，其中任意的μ∈C，k∈K，x∈Μ，若具有性质:

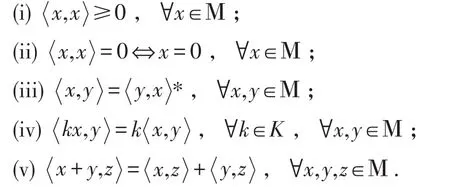
定义1.2[2]称序列{vλ,λ∈Λ}为Hilbert K-模 Μ的标准正交序列，若对∀λ,μ∈Λ，

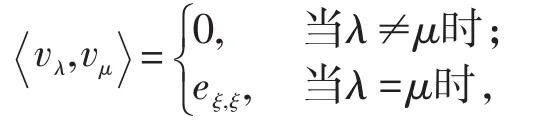
其中ξ∈H，且 ‖ξ‖=1(H为Hilbert空间)，eξ,ξ∈K满足： ∀η∈H，eξ,ξ(η)=(η,ξ)ξ.其中，(·,·)指 Hil⁃bert空间中元素的内积；若该标准正交序列完备，即,∀λ∈Λ，则称它为Μ的标准正交基，将eξ,ξ称为支撑投影.

定义1.3[2]称Hilbert K-模Μ中的序列{eξ,ξxλ,λ∈Λ}为框架，若存在常数a＞0,b＞0，使得对∀x∈M，

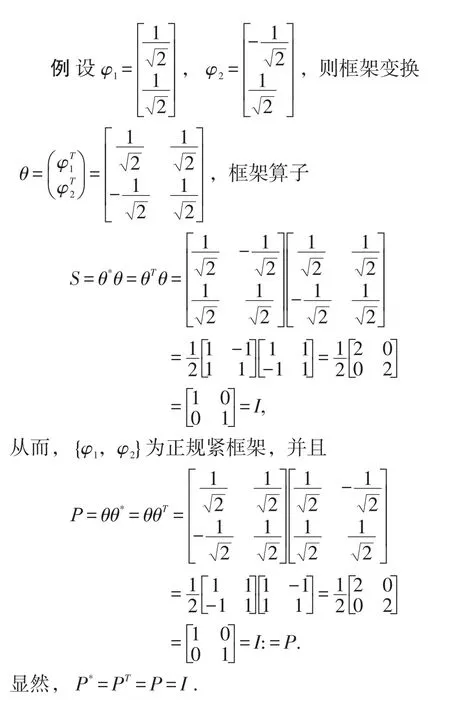
若a=b，则 称 {xλ,λ∈ Λ}为紧框架；若a=b=1，则称{eξ,ξxλ,λ∈Λ}为正规紧框架.

定义 1.4设M为 Hilbert K-模，{eξ,ξxλ,λ∈Λ}

2 Hilbert K-模上框架的分解

3 框架变换与正交投影之间的关系