基于抛物方程法的主动雷达探测威力评估方法
2020-06-05匡华星王玲玲
周 亮,匡华星,王玲玲
(中国船舶集团有限公司第八研究院,南京 211153)
0 引 言
作为编队的“眼睛”,舰载雷达在战场环境中起到的作用至关重要,能够直接影响着战略决策的制定。因此,对于主战雷达的工作性能评估问题,无论在设计阶段还是在实装阶段或者在复杂的战场电磁环境中都具有重要的参考价值。
在上世纪90年代初,美国海军就开始研究电波在海面低空大气中传播的折射效应,并基于射线跟踪算法开发了名为“工程折射效应预测系统(Engineer’s refractive effects prediction system, EREPS)”。EREPS用于计算海面低空环境下雷达传播的干涉、绕射、对流层散射和海面大气波导层的折射效应,为雷达、电子战、通信系统提供海区电磁特性数据。[1-2]1998年,美国空间和海军作战系统中心(Space and Naval Warfare Systems Center, San Diego)大气传播分部(Atmospheric Propagation Branch)的研究小组在EREPS的基础上建立高级折射效应预测系统(Advanced Refractive Effects Prediction System, AREPS)的软件平台。[3]作为EREPS的更替版本,AREPS主要选用抛物方程(Parabolic Equation, PE)方法作为其核心求解算法。这种电波传播模型能够用于预测复杂大气条件下海面上的电波传播特性,准确预测各种不规则地形对电波传播产生的反射、折射和绕射效应。因此,AREPS是一个可以预测复杂环境下电波传播特性的电磁环境评估系统,主要应用于美国海军各基地的指挥自动化、雷达、电子战和军事通信系统[4-6],为战场态势评估提供电磁环境参考数据。[3]
国内电子科技大学[7]、电波传播研究所(中电22所)对抛物方程方法也展开了深入的研究,但主要侧重于电波传播路损的计算上,对于抛物方程法的具体应用研究较少。但是,雷达的工作性能除了受到电波传播特性的影响还取决于雷达本身的工作参数和目标的散射特性,仅通过电波传播特性来评判雷达的工作效能是不足的。
针对上述问题,提出一种基于抛物方程模型的多模型评估方法,结合了雷达方程、抛物方程和目标闪烁模型,采用抛物方程模型评估电磁波的空间传播路径损耗,并采用雷达方程模型来引入雷达具体工作模式下的工作参数,通过结合目标散射特性计算目标回波功率及信噪比,最后通过Swerling目标闪烁模型来求解目标在噪声环境中的检测概率。程序采用面向对象的方法来进行编写与集成。这种方法能够用于分析和评估雷达在各种大气环境的工作性能,以获取量化后的实际指标,具有重要的工程应用价值。
1 基于抛物方程模型的电波传播特性算法
抛物方程法基于亥姆赫兹方程推导而来,负时谐电场的复包络满足

其中,正负号分别代表前向和后向传播的电磁场分量所满足的支配方程,利用收发互易定律,雷达前后向传播的空间路径损耗相等,忽略后向传播分量可得到抛物方程模型,其完备地描述了电磁波前向传播的过程。
为了对抛物方程进行数值求解,需要处理根号及二次微分项,采用Feit-Fleck来进行近似:
将Feit-Fleck近似代入抛物方程后进行化简,得到

从电场支配方程可以看出,电磁波的传播过程中同时存在衍射和折射两种传播效应。衍射效应在角谱域(频域)用传播方向的波数分量进行描述,折射效应在空域(时域)用相位滞后进行描述。将这两种效应在不同的作用域分别予以处理,得到抛物方程的分步傅里叶解法(Split-Step Fourier Transformation, SSFT),其步进表达式[11-13]为
采用傅里叶变换对复杂的空间场进行分解,将其分解为多个平面波的叠加,再根据平面波的解析传播公式得到下一个步进面上的远场,通过逆傅里叶变换获得空间场分布。在表达式中,空域(x,y)和角谱域(kx,ky)互为傅里叶变换对,空间傅里叶变换关系式为
在步进求解的过程中,空间初始场根据雷达天线的位置(x0,y0)和波瓣宽度(θx,θy)设置为
由于边界处的条件不同,在边界位置的处理方法也有所区别。上边界和左右边界为自由空间,因此其需要加上半边窗函数(汉明窗)来处理数据截断,用于模拟无反射边界。汉明窗的计算公式为w(n)=0.54-0.46cos(2πn/N),0≤n≤N。下边界为地/海边界,在求解的过程中需要结合镜像法[14-15]来完成,即有u(-x,y)=-u(x,y)。
抛物方程能够计算雷达-环境-目标链路之间的单程路径损耗,具体求解步骤如下:
(a) 根据雷达天线的波瓣宽度、架设位置、工作频率,计算初始场的空间分布;
(b) 上半空间场乘以折射因子,考虑空间中不均匀大气产生的影响;
(c) 下半空间场在边界处进行镜像,考虑地/海边界产生的多径效应;
(d) 傅里叶变换完成近场到远场的转换,将空间场变换为方向图,实现平面波分解;
(e) 在远场乘以衍射因子,考虑平面波的衍射效应;
(f) 傅里叶逆变换完成远场到近场的转换,将平面波综合为空间场分布;
(g) 通过步进公式(b~f)进行计算,分析所有位置的空间场强分布;
(h) 如果使用的是二维抛物方程模型,计算场强还需要除以距离的开方值。
2 主动雷达探测威力评估方法
基于抛物方程模型,可以建立主动雷达的探测威力评估模型,主要包含雷达方程、抛物方程及目标闪烁检测模型。本节对雷达方程和目标闪烁检测模型进行介绍。
2.1 雷达方程模型修正
雷达方程模型建立了雷达工作参数与目标回波功率之间的联系,通过发射功率、收发天线增益、接收机噪声单边功率谱密度、目标散射截面积大小等参数,获得雷达接收到的目标回波及信噪比随距离的变化曲线。在脉冲压缩体制下,雷达采用的收发波形为线性调频连续波或相位编码波形,需要考虑脉压增益,采用回波能量而非功率进行建模描述。
雷达接收到的目标能量为
其中,Pt为脉冲的峰值功率,Gt为发射天线增益,τ为脉冲宽度,R为目标与雷达的距离,σ为目标散射截面积,Ar为雷达接收天线的截面积。式中第1部分为雷达单脉冲传播至目标处的能量,乘以第2部分得到经目标散射后回到雷达位置的能量,乘以第3部分后得到雷达接收能量。
经过雷达接收机的处理后,目标单个脉冲回波的信噪比为
SNR=E/N0
其中,E为单脉冲的回波能量;N0=kTe为接收机噪声的单边功率谱密度,k=1.38×10-23(J/K)为波尔兹曼常数,Te为接收机的总等效噪声温度,其包含天线的噪声温度Tant、接收机工作温度Trx、接收机噪声因子Frx等因素。
Te=Tant+Trx(Frx-1)
雷达方程模型主要基于自由空间环境建立,仅能够用于分析对空探测威力;其在对海探测威力分析时并不适用。对雷达方程进行改进,使其能够用于主动雷达的对海探测威力评估,具体方法如下所示:
其中,双程路径损耗为抛物方程计算的单程路径损耗的平方。由于抛物方程计算得到的是复场强的空间分布,将其转换至路径损耗时需要进行校准,校准公式为
PLfs=4πΔz2
PLpe=|u(x,y,z)|2/|u(x0,y0,Δz)|2·4πΔz2
其中,u(r,z)为抛物方程计算得到的场强的空间分布,Δz为距离方向的单个步长。
2.2 目标闪烁模型
雷达探测目标的过程中往往会采用相干或非相干积累的方式来提升目标回波的信噪比,目标检测概率主要和回波信噪比、累积脉冲数、驻留时间相关。此外,目标的检测概率与目标闪烁类型有关,共分为5种起伏目标模型。对于Swerling起伏目标的检测性能如表1公式所示。


表1 起伏目标的检测概率
在获取目标回波信噪比随距离变化曲线之后,结合目标闪烁模型,即可获得目标检测概率。
3 实验验证
为了验证电波传播模型的正确性,采用射线追踪模型和AREPS数据来进行验证。雷达工作在C波段,天线的垂直方向波瓣宽度为3°,雷达架设高度为15.24 m,计算高度为500 m,计算距离为185.2 km。
从计算结果中可以看出,带基础层的大气波导在波导层结中能够陷获电磁波,电磁波的泄露较少,因此能够传播至较远的区域。与射线追踪模型相比,抛物方程预测结果能够给出定量的路径传播损耗。这两种模型给出的雷达盲区较为接近。将海面高度12和120 m两个高度上的路径损耗取出,与AREPS软件结果进行对比,可以看出两者吻合程度较好,平均误差小于3 dB,说明程序具有准确性。图1为带基础层的表面波导环境中抛物方程模型与射线模型的对比。图2为带基础层的表面波导环境中抛物方程模型与AREPS的数据对比。

图1 带基础层的表面波导环境中抛物方程模型与射线模型的对比

图2 带基础层的表面波导环境中抛物方程模型与AREPS的数据对比
在对程序的正确性进行验证之后,开发了基于组合模型的雷达系统性能评估软件。在设置完成大气媒质环境、雷达工作参数后,可以对雷达的探测威力进行评估。图3为基于组合模型的雷达系统性能评估软件。
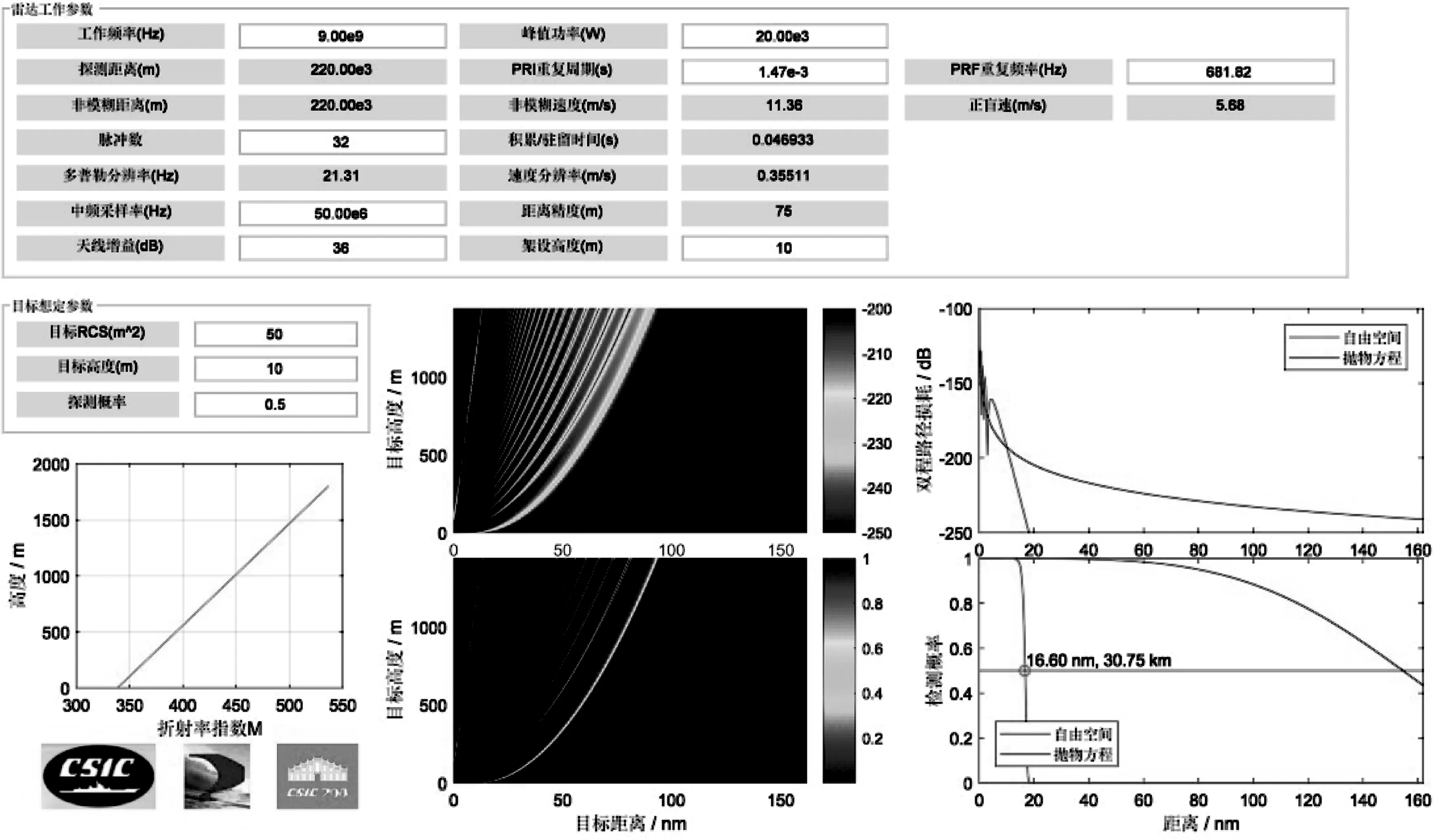
图3 基于组合模型的雷达系统性能评估软件
4 结束语
本文提出了抛物方程、雷达方程、目标闪烁模型的组合模型,能够很好地分析雷达电磁波的空间传播特性,据此评估出雷达的探测威力指标。通过与AREPS软件的对比,验证了算法的正确性和有效性。该算法能够应用在雷达设计和定型阶段,具有一定的工程应用价值。
