基于聚类分析水质指标相关性研究

郑泽豪

(重庆交通大学 河海学院，重庆 400074)

对流域实行长期水质监测，旨在科学评估河流的水质状况及掌握水质变化规律，是流域水环境管理的基础性也是重要性的工作。为有效、准确地反映流域水体水质状况，需要建立合适的水质监测网络。随着监测网络范围的扩大，大量监测数据产生的同时，监测成本也必然随之增加。在对获得的指标数据分析的同时，进一步深入分析各指标之间的内在联系，对优化水质监测网络有重要意义。对于有着长时间序列，多个监测指标，多个断面的流域，采取何种统计分析方法对动态监测数据进行挖掘和综合分析，并借此指导水质监测网络的优化、提高监测点的代表性，是水质监测和评价的研究重点和方向[1]。

随着水体环境研究的不断深入，多元统计分析方法被广泛运用到水质评价实践中，根据部分学者所做的研究发现，对于存在多指标的监测数据，运用聚类分析统计法可以做出更为客观、准确的评价[2]。本文水质数据分析采用层次聚类分析方法，通过对水质指标的相关系数进行聚类，分析比较各水质指标之间的相关关系，对具有相关关系的指标进行聚类，并对聚类结果进行回归检验，实现降低水质指标维数的目的，为流域水质监测工作的优化提供一定的科学依据。

1 研究区域与研究方法

1.1 研究区概况

研究区是淡水河一级支流，属于东江水系。流域受南亚热带季风气候影响，全年温度适宜，丰富的降水给河道带来大量的水资源。河道干流全长为13余km，流域面积约为129.4 km2。根据区域内雨量站1961—2014年实测年雨量资料统计显示，多年降雨平均值为2 073.5 mm，且雨量在年内每月分配严重不均，表现为每年4—9月有大量降雨，降雨量约占全年雨量的85%[3]。多年以来，区域内平均年径流深为1 050 mm，平均水面蒸发量为1 345.7 mm。

本文选取了6个监测断面，选取的监测指标为PH、溶解氧(DO)、高锰酸盐指数(CODMn)、氨氮(NH3-N)、总磷(TP)、总氮(TN)和化学需氧量(CODCr)等7项。数据资料为2018年6个监测断面7项监测指标的连续监测数据，按照国家环境质量标准《地表水环境质量标准》(GB 3838—2002)[4]进行评价。

1.2 研究方法

聚类分析法是将研究的样品或变量之间的相似程度大的先归为一类，把另外还具有一定相似性的聚为一类，然后继续聚类进程，最终将所有样本或变量都各自分类，达到“物以类聚”的效果。运用较多的聚类分析算法有层次聚类算法(HCA)、K-Means聚类算法、自组织映射聚类算法(SOM)等[5]，其中层次聚类分析应用最为广泛，层次聚类分析又分为Q型(样本分类)和R型(变量分类)。通过挖掘样本或变量之间的相似性，将相似程度大的统计量作为代表进行分析，可以简化数据即减少变量个数，达到变量降维的目的[6]。本文意在通过R型聚类分析的方法，在多个水质指标中筛选出能够代表其他指标的变量，将该变量与其他指标进行相关性分析，降低指标维数，优化水质监测及评价工作。

2 数据处理与分析

2.1 数据标准化处理

对数据标准化处理是进行数据分析的一项首要工作，尤其是对于基于距离的算法更为重要。零-均值标准化(标准差标准化)是一种常见的将数据标准化的方法，经处理后的数据符合正态分布，故本文采用此法[7]：

(1)

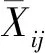
2.2 水质指标相关性分析

经过标准化后的数据，可计算各变量之间的相关系数。聚类分析算法是按照各变量之间存在的差异性进行分析的，而变量间的差异性通过距离反映，距离越近，相似性越明显。距离量度方式有多种，本次选用皮尔逊相关系数量度各变量之间距离，数学定义为[8]：

(2)

式中n为样本总数；xi和yi分别为两变量的变量值。

利用SPSS25.0计算各水质指标之间的相关系数矩阵结果可参见表1。

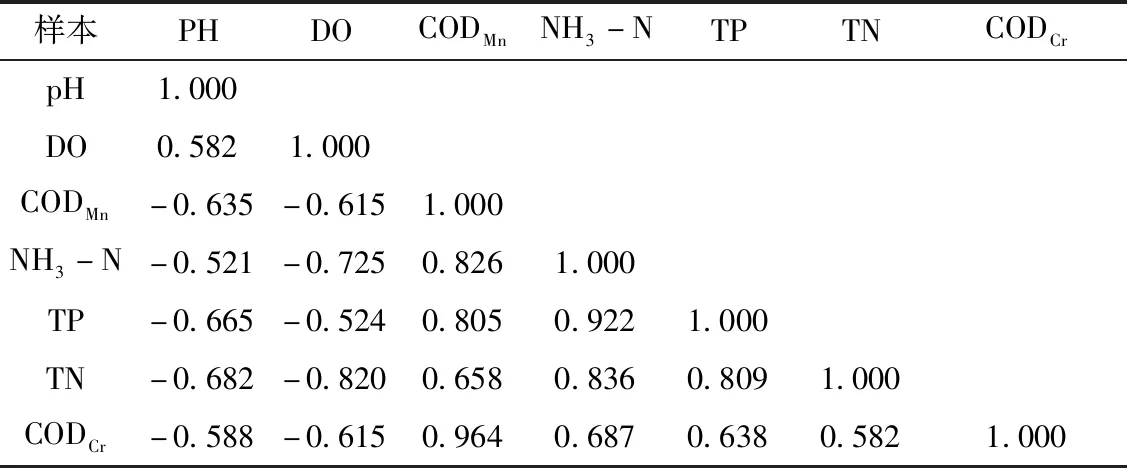
表1 各水质指标相关系数矩阵

若算得相关系数的绝对值越大，则两指标间的关系越紧密[9]。由矩阵结果表1可知，该河水质指标中CODMn与CODCr相关性最好，TP和NH3-N相关性排在第2位，其他指标之间的相关性弱于上述两者。根据污染源普查统计得到，沿岸部分企业COD、NH3-N和TP的直排入河量占总排放量的13%、15%和19%，且研究区为城市河流，流经居民区和农田，截污纳管率较低，河道为污水、污物受纳终端，长期的生活污水和农业面源污染排入河道，是NH3-N和TP的主要来源。CODMn与CODCr作为地表水常规监测项目，可反映水体受有机物污染的状况；TP和NH3-N是河流治理中污染物排放控制的两个重要因子。若两两之间存在相关关系，则可用CODCr浓度估算CODMn浓度，用NH3-N的浓度估算TP的浓度，以对浓度监测值进行预测，降低监测频次，提升应急监测能力。

2.3 水质指标聚类分析

由相关系数矩阵可知各指标间的亲疏关系，为更明了地观察结果，对相关系数进行R型聚类分析，类与类间距离采用组间平均链接距离计算，一步步将各统计量归为一类，作出聚类树形分类示意(见图1)。

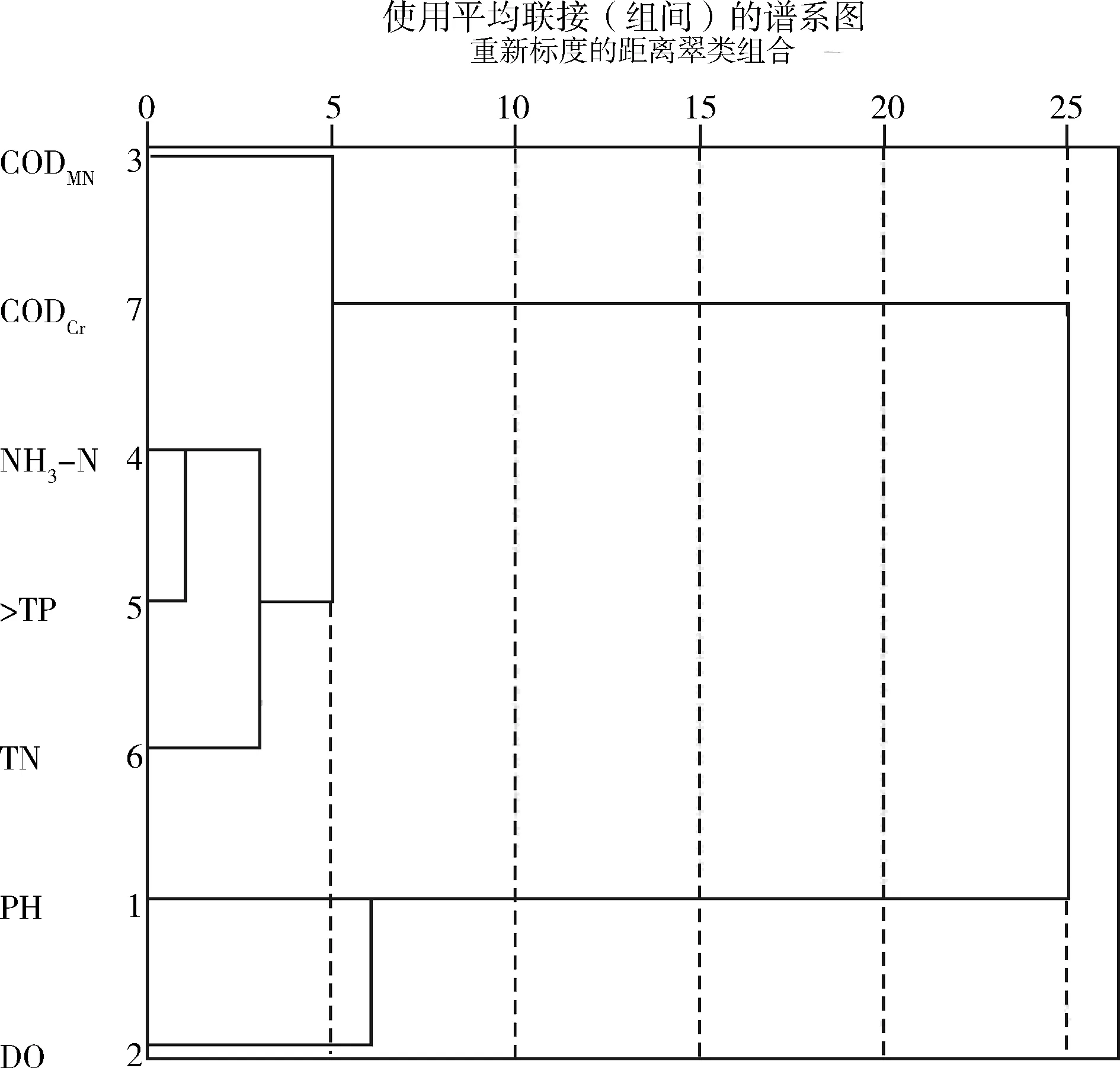
图1 各指标聚类树状示意

由SPSS软件生成的树状示意可以看出，CODMn和CODCr两者、NH3-N和TP两者距离最为接近，两两连线合并成一类；接着是TN与(TP、NH3-N)连成一类，它们间的距离大于NH3-N和TP距离；然后是前两个大类合并为一类，以此逐级连线的方式将所有个体聚成一类。结合相关系数矩阵和聚类分析结果可知，CODMn浓度和CODCr浓度、NH3-N浓度和TP浓度之间的相关性极其显著。

2.4 线性回归分析

为了更好地描述水质指标间的线性关系，明确水质指标间的数学统计关系，采用回归方程验证的形式，利用SPSS软件分别对CODCr和CODMn、NH3-N和TP进行回归分析，线性回归关系如图2，线性回归过程如表2。从图2中可以看出CODMn值随着CODCr值增大呈现总体增大的趋势，TP值随着NH3-N值增大而增大。由表2可知，在CODMn=a×CODCr+b表达式中，a=0.140，b=1.549，R2=0.629，t检验值为3.868，与P=0.05相当的临界值t0.05=2.030相比，P<0.05，符合差异性检验，表明CODCr浓度和CODMn浓度存在线性回归关系。同理，在TP=a×NH3-N+b表达中，a=0.069，b=0.230，R2=0.598，t检验值为3.376，符合差异性检验，表明NH3-N浓度和TP浓度存在线性回归关系。综和上述分析，列出CODCr和CODMn、NH3-N和TP的线性回归关系式：

(3)

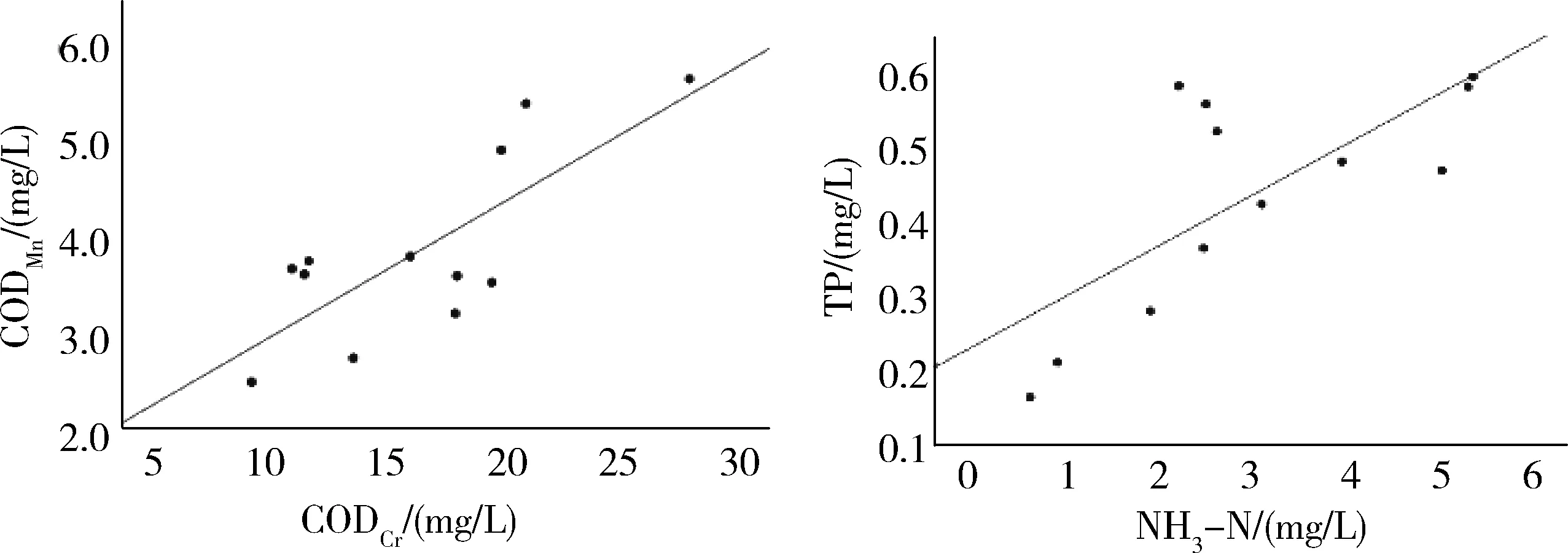
图2 线性回归拟合示意

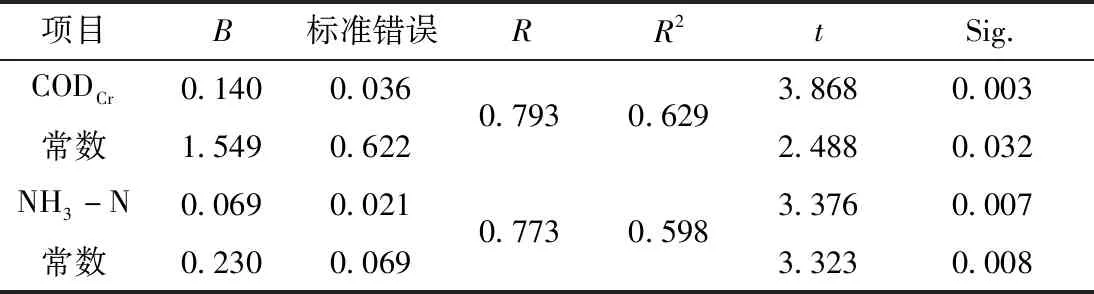
表2 线性回归过程

2.5 线性回归检验

为了验证2.4中统计的两个线性回归方程的适用性，选取2018年1—12月断面X的CODCr和NH3-N监测值，分别计算CODMn和TP的浓度，并与断面X实测的CODMn和TP浓度值进行对比，结果见表3。由表3分析知，断面X全年的监测值与计算值之间的相对偏差小于5%的数据超过50%，说明统计得到的线性回归关系式具有较强的的实用性和较高的准确性。

表3 断面X数据对比 mg/L

3 结语

1) 通过对监测的水质指标间的相关性进行分析，确定水环境中的CODCr和CODMn、NH3-N和TP关系密切，统计得到的回归方程关系式满足拟合度检验，表明指标间具有较强的线性相关关系。

2) 本文通过对相关关系矩阵进行聚类分析，筛选出相关系数最大的指标，用较少的指标表示研究区域的水体质量，减少了指标重叠的情况，说明本文运用的方法在有大量监测数据的情况下，可以降低水质指标的维数，简化数据，优化水质评价过程，达到降低水质监测成本的目的。

3) 针对有多指标、长时间监测数据的区域，可以根据本文的方法，对各断面水质指标进行多元统计分析，明确河流污染状况，为其它地表水水质指标间相关性研究提供参考。