基于贝叶斯优化的心脏病诊断模型
2020-06-04杜一平
杜一平
(吕梁学院 数学系,山西 离石 033001)
心脏病的诊断是一个分类问题,数据挖掘中基于分类的模型有很多,如KNN、logistic回归、决策树、支持向量机、神经网络等.而近几年集合多个学习器的集成学习模型在各方面表现出其优越性,得到人们的追捧.如随机森林、AdaBoost算法.随机森林是对多个决策树的并行组合,AdaBoost则是对其进行串行迭代.单个学习器的准确率只依赖于自身单一参数的选择,而集成学习模型虽然有更强的泛化能力,但往往有数量众多的参数需要进行选择.如果参数多且其取值空间非常大,想要进行参数择优就是一个难题.遍历整个参数空间,往往是不现实或者是效率极低的.而如果用随机搜索的方法则很有可能遗漏最优值.对于参数集的选择问题,贝叶斯优化框架是一个非常有效的办法[1].
1 贝叶斯优化框架
贝叶斯优化实质就是在对目标函数具体形式不知的情况下,根据已有的采样点来估计函数最大值的一种算法.与遍历搜索算法相比,迭代次数少,粒度小[2].优化流程如图1:
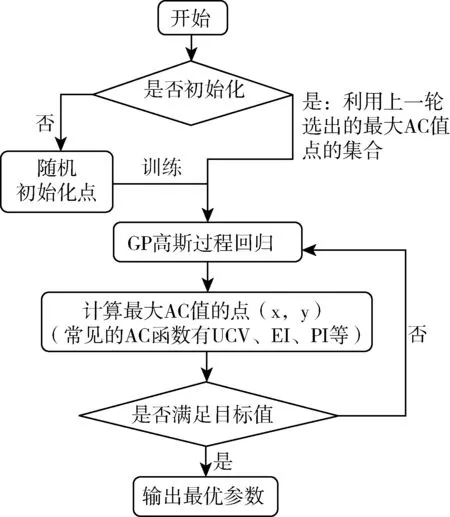
图1 贝叶斯优化流程
贝叶斯优化流程有两个主要模块,概率代理模型(Probabilistic Surrogate Model)和采集函数(Acquisition Function).
1.1 概率代理模型
概率代理模型顾名思义就是用一个概率模型来代理目标函数f(·).模型更新由式(1)得出.
(1)
其中,D={(x1,f1),(x2,f2),…,(xn,yn)}表示已采集样本点,p(f)为f的先验分布,通过贝叶斯公式得出p(f|D)为f的后验分布.具体的代理模型根据参数的不同情况,可以分为参数模型和非参数模型.参数模型就是由参数w来决定f(·),它的参数量在更新过程中是不变的.而非参数模型的参数量会随着数据量的变化而变化.相比较,非参数模型要更灵活、更具扩展性.非参数模型中应用最广泛的是高斯过程(GP)[3].
高斯过程本质是一个多元正态分布,在贝叶斯优化中,一般假设:
(2)
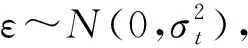
y|X,σ2~N(y|m,K+σ2~I)
(3)
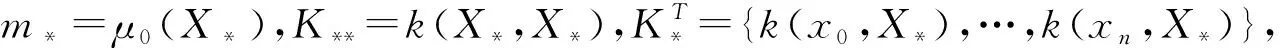
(4)
1.2 采集函数
采集函数的目的是在参数空间中得出下一个评估点,使其能提升函数性能.常见的采集函数有:UCB、PI、EI三种.本文中采用PI函数,其形式为:
PI(X)=p(f(X)≥f(X+)+v)
(5)
式(5)中f(X)为目标函数,f(X+)为目前为止最优的目标函数,μ(x),σ(x)是f(X)后验分布的均值和协差阵,v权衡系数,避免陷入局部最优.采集函数过程就是选取新的X,使PI(x)最大,一般这个过程使用蒙特卡洛模拟方法[4].
2 贝叶斯优化的心脏病分类模型
文章选取UCI心脏病数据集Heart,数据集中有303条数据,15个属性,其中Ca表示患有心脏病可能性.部分数据如下:

表1 Heart数据集5个样本数据
2.1 数据预处理
在R中导入数据集Heart,发现有少量缺失值,直接进行剔除,剩余297条数据.对变量RestBP、Chol、Thalach、MaxHR进行标准化处理.数据集中描述心脏病可能性的变量Ca是一个连续型变量,创建一个AHD变量,将Ca二值化.当Ca的值大于等于0.5时,AHD取Yes,反之取No.以AHD作为分类变量,建立分类模型.
2.2 建立分类模型
本文采用当下流行的集成学习中的随机森林算法建立分类模型.随机抽取50个样本作为测试集,其余为训练集.随机森林模型参数主要有两个[5]:第一个是树的数量Ntree,数量过多过拟合的风险增大,数量太少又欠拟合,其范围确定为(1,120).第二个是建树时随机抽取的属性个数Dtree,取值范围(1,14).接下来用贝叶斯优化算法对参数进行优化.
首先确定目标函数.对于每组参数所对应的模型,在训练集上进行5折交叉验证,平均误差为目标函数f,每组参数组合为变量X,代入贝叶斯优化框架中进行迭代计算,参数优化流程见表2.

表2 参数优化流程
2.3 结果分析
本文采用R语言中MIBayesOpt程序包.它提供了支持贝叶斯优化方法的计算框架,辅助支持向量机、随机森林等模型进行参数优化.计算框架中采用GP+PI模型,即高斯过程结合PI函数的优化模型,对随机森林模型的参数进行优化搜索,搜索迭代次数为100次,得出最优参数组合(Ntree,Dtree),测试集准确率达到93.44.接着采用随机选取的方法,随机选出100组参数组合,得出其准确率最高的组合为(Ntree,Dtree)=(110,6).将两组参数代入随机森林模型在测试集上分别测试分类准确率.表3和表4分别代表两种模型的在测试集上的性能,结果汇总如表5.
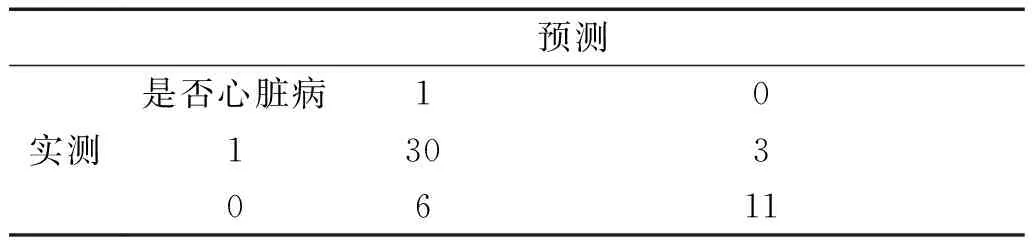
表3 随机搜索模型混淆矩阵
表4贝叶斯优化模型混淆矩阵
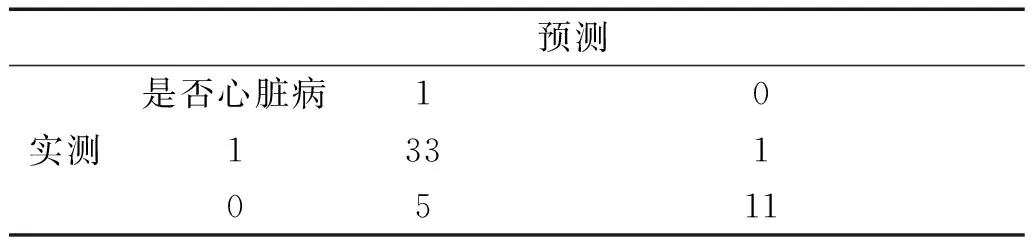
预测实测 是否心脏病1013310511

表5 结果比较
由实验结果可以得出,贝叶斯优化寻参方法与随机搜索方法相比,在迭代次数相同的情况下,在测试集上准确率要更高.因此随机搜索最优参数还是具有一定的盲目性,而贝叶斯优化寻参方法是随着数据模型变化趋势,有目的的寻找最优参数,效率更高.
3 结束语
本文首先简要介绍了贝叶斯优化框架的理论知识,随后将其框架应用于随机森林分类算法的参数寻优过程中.最后经Heart数据集实证分析,得出其方法在调参方面的优越性.贝叶斯优化框架也可以广泛应用于其他机器学习模型的参数调优中.
