载机平台光电转塔目标定位的仿真算法

秦 川，吴玉敬，陶 忠，桑 蔚，安学智

（西安应用光学研究所，陕西 西安 710065）

引言

机载光电目标定位任务主要由载机、光电转塔和GPS/惯导（INS）三大系统组成。其中GPS/INS提供载机的经纬高信息和姿态信息（包括真航向、俯仰角、横滚角），光电转塔完成对目标的搜索、捕获、定位和跟踪等功能，其瞄准目标后可提供瞄准线（LOS）的方位、俯仰角等信息（涵盖光电转塔方位、俯仰角和目标横向、纵向像素偏差角），结合传感器本身参数（包括视频显示的方位、俯仰视场角和视频显示的横向、纵向分辨率）即可实现对海平面目标的无源定位任务。若结合安装于光电转塔内的激光测距机给出的测量信息，则可实现三维空间目标的有源定位任务。

在海面目标的无源定位过程中，目标与载机的距离信息并非直接测量，因此需要：1）用载机高度的负值近似目标在载机东北天坐标系下的zG值，进而求解距离R的近似算法；2）结合地球椭球模型，进而求解距离R的严格解析算法。此外，无论GPS/INS 还是转塔视轴稳定度、视频像素偏差读取、激光测量距离等都存在一定误差，这些误差近似呈Gaussian 分布，所以每次定位结果都会或多或少偏离目标真实位置，这在实际定位过程中是需要尽可能降低的，并且定位精度作为光电转塔核心作战技术指标之一也需要预先估计出来。

文献[1]对车载光电侦查系统的目标定位模型及误差源进行了分析并通过外场试验加以验证；文献[2]分析了多光谱图像的定位与配准，特别是对地理定位误差源进行了探讨；文献[3]对定位精度的评价指标进行研究，指出均方根误差、平均误差及置信概率区间方法的计算原则及使用条件；文献[4]分析了测量平台中的坐标转换误差，给出载机姿态精度、位置精度提升对定位结果的影响大小；文献[5]分析了光电侦查系统的定位精度影响因素，提出对INS 的误差控制建议；文献[6]分析了机载光电观瞄系统的目标定位原理，对算法进行了试验研究；文献[7]基于激光测距，对有源目标定位技术进行了研究；文献[8]～[10]也对相关定位问题进行了讨论。

本文基于载机平台光电转塔目标定位需求，分析了有源、无源目标定位的算法，其中对于海面目标无源定位，目标载机距离的计算采用严格的解析算法；对于定位精度的预估，本文提出转塔视轴反演算法，并结合前者定位算法及Monte-Carlo 分析方法，从仿真角度得出一定测量精度条件下的海面目标无源定位精度，即圆概率误差（CEP）半径约39.4 m@80%置信度及约18 km 距离；此外还做了载机位置、姿态、转塔视轴不同时对目标定位的80%置信度CEP 半径、最大误差距离等统计直方图分析。本文的仿真方法及结果对于目标定位研究具有一定的理论指导意义。

1 基本定义

1）地球椭球

在控制测量中，代表地球的椭球称作地球椭球，它是地球的数学模型。地球椭球的几何定义为：O是椭球中心，NS（南北极）为旋转轴，a为长半轴（取值6 378 137 m），b为短半轴（取值6 356 752 m）。赤道定义为：通过椭球中心的平行圈。纬圈定义为：垂直于旋转轴的平面与椭球面相截所得的圆。子午圈定义为：包含旋转轴的平面与椭球面相截所得的椭圆。其第一偏心率和第二偏心率分别为

2）载机机体直角坐标系（OA-XAYAZA）

载机机体坐标系为三维直角坐标系，坐标系的原点OA为载机质心，XA轴为载机右翼正向，向外为正，YA轴为载机纵轴机头正向，ZA轴通过右手螺旋定则确定，垂直XAYAZA平面朝向机身上方。

3）东北天直角坐标系（OG-XGYGZG）

东北天坐标系为三维直角坐标系，坐标系的原点OG为载机质心，XG轴指向正东，YG轴指向正北，ZG轴沿地垂线指向天空。

4）地心直角坐标系（Od-XdYdZd）

地心直角坐标系为三维直角坐标系，原点Od为参考椭球体中心，Zd轴与参考椭球体旋转轴重合，向上为正，Xd轴为格林尼治子午面与地球赤道平面的交线，向外为正，Yd轴在赤道平面内，并与Xd、Zd成右手直角坐标系。

5）相对直角坐标系（OR-XRYRZR）

相对坐标系是为了实现东北天坐标系到地心直角坐标系的转换，自主定义的三维直角坐标系。其原点OR为载机质心在地球表面的投影，XR轴与Od-Xd平行且方向一致，YR轴与OR-YR平行且方向一致，ZR轴与OR-ZR平行，且方向一致。

6）空间大地坐标系（WGS-84，LBH）

空间大地坐标系就是WGS-84 世界大地坐标系，是美国国防部于1984年定义，通过大地经度（L）、大地纬度（B）和大地高（H）来描述空间位置。经度是空间中的点与参考椭球的自转轴所在的面与参考椭球的起始子午面的夹角，纬度是空间的点与参考椭球面的法线与赤道面的夹角，大地高是空间点沿参考椭球的法线方向到参考椭球面的距离。

7）载机姿态（θεγ）

载机姿态包括真航向（θ）、俯仰角（ε）和横滚角（γ），采用惯导进行测量。真航向定义为飞机所在位置的真经线北端顺时针测量至航向线YA轴的夹角，北偏东为正。俯仰角定义为机体YA轴线与地平面间的夹角，以飞机抬头为正。横滚角定义为机体ZA轴与包含机体YA轴的铅垂面间的夹角，以飞机向右倾斜为正（尾追观察）。

8）光电转塔方位角（Tx）和俯仰角（Ty）

以载机坐标系为基准，光电转塔光轴偏离XAYA平面的角度称为俯仰角，光轴抬头为正；光轴在XAYA平面的投影偏离YA轴的角度称为方位角，投影向右偏离为正（俯视观察）。

9）目标横向像素偏差角（σx）和纵向像素偏差角（σy）

目标在视频显示屏上距离光轴的像素偏差，向右向上为正。

10）目标的稳瞄瞄准线俯仰角（α）和方位角（β）

目标的稳瞄瞄准线俯仰角和方位角分别定义为

关于2012年的水利规划计划工作，陈雷部长提出了明确要求，学文同志进行了具体的布置。这里，我再强调以下三项工作的落实。

式中：Vx、Vy分别为视频显示的方位和俯仰视场角；Rx、Ry分别为视频显示的横向和纵向分辨率。

2 坐标系转换

2.1 目标的瞄准线俯仰角、方位角和载机机体直角坐标系的转换

显然，目标的稳瞄瞄准线俯仰角、方位角到载机机体直角坐标系间转换关系为[11]

式中：R表示目标距载机距离，对于有源目标定位，该值来自激光测距机等的信息。对于无源海平面目标定位，该值可以采用两种方法获得：其一是近似方法，其二是严格解析方法。这两种方法都先假设（5）式中R为未知变量，然后根据近似条件或者解析条件算出R，最后再带入（5）式中重新计算目标的载机机体直角坐标值。

载机机体直角坐标系到稳瞄瞄准线俯仰角、方位角间转换关系为

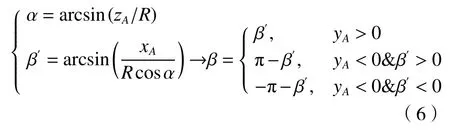
2.2 载机机体直角坐标系和东北天直角坐标系的转换

载机机体直角坐标系到东北天直角坐标系间转换关系为[11]

其中转换矩阵A为

对于海平面目标，可近似假设zG=-H，从而求出R的近似表达式：

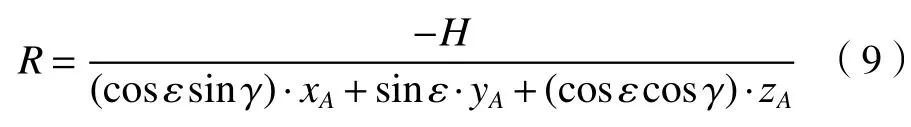
东北天直角坐标系到载机机体直角坐标系的转换关系为

2.3 东北天直角坐标系和相对直角坐标系的转换

东北天直角坐标系到相对直角坐标系的转换关系为[11]

其中转换矩阵C为

相对直角坐标系到东北天直角坐标系间转换关系为

2.4 相对直角坐标系和地心直角坐标系的转换

相对直角坐标系到地心直角坐标系间转换关系为[11]

式中N为载机所在椭球卯酉圈曲率半径，计算公式为

对于海平面目标，其位于地球椭球面上，满足：

因此，可通过求解含有R的一元二次方程得到目标与载机的距离信息解析值。

地心直角坐标系到相对直角坐标系间转换关系为

2.5 空间大地坐标系和地心直角坐标系的转换

空间大地坐标系向地心直角坐标系的转换关系为[12]

式中：LT、BT、HT分别为目标的经度、纬度和高度；NT为目标所在椭球卯酉圈曲率半径。

地心直角坐标系向空间大地坐标系的转换关系为[13]

式中：BT和HT的求解含有交叉项，可以通过zd/sqrt（xd2+yd2）先求出BT的初值，然后利用BT的初值结合（15）式和（19）式，即可以求出NT、HT的初值，接着再次求解BT的值，循环往复，直至满足精度要求[13]。BT、HT也可以采用解一元四次方程的方法[12]，或者Bowring 解法[14]：

3 仿真分析

3.1 算法流程

对于目标定位，即是已知载机经、纬、高（LBH）、载机姿态（θεγ）、光电转塔瞄准线方位角（Tx）和俯仰角（Ty）、目标横向像素偏差角（σx）和纵向像素偏差角（σy）、视频显示的方位和俯仰视场角（Vx和Vy）、视频显示的横向和纵向分辨率（Rx和Ry），求解目标的空间大地坐标（LTBTHT）。若目标与载机的距离R已知，则是有源定位；若未知，则是无源定位。对于有源定位，目标不必限定位于地球表面；而对于无源定位，若只通过载机和光电转塔一组测量数据进行解算，必须限定目标位于地球表面。

与定位过程相反的过程，即是光电转塔视轴反演过程，即已知载机LBH、θεγ，光电转塔σxσy、VxVy、RxRy，目标LTBTHT等信息，求解光电转塔的TxTy。

本文采用R的解析求解方法和BT、HT的直接求解方法，其算法流程如图1所示。其中图1（a）过程对应光电转塔视轴反演，图1（b）过程对应有源目标定位，图1（c）过程对应无源目标定位。

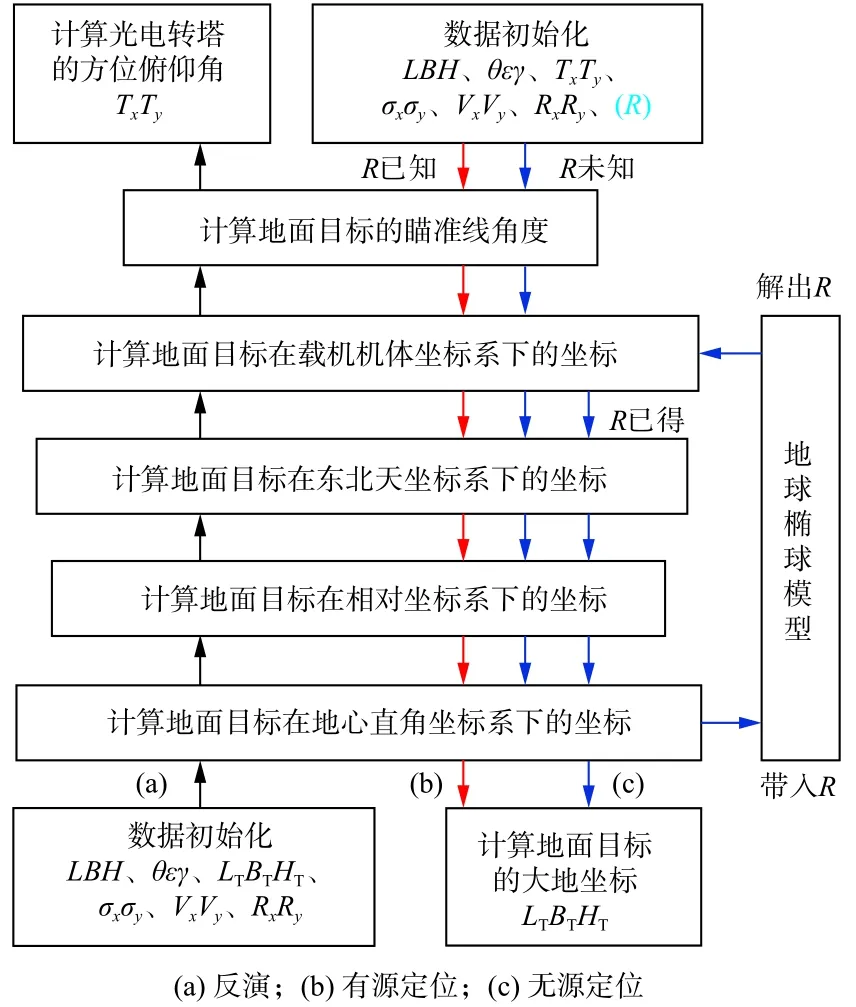
图1 目标定位与反演算法流程Fig.1 Flow diagram of target location and inversion algorithms

3.2 光电转塔视轴反演

假设目标在（东经108°53′53″，北纬34°12′45″，高度426.6 m），传感器视场0.45°×0.25°，分辨率1 920×1 080 像素，载机飞行速度为400 km/h，运动轨迹如图2所示，即载机在6 000 m 高度先向北平飞，然后逆时针做3/4 圆周盘旋，接着开始向东爬升高度至7 000 m 后平飞，姿态依照飞行航迹相应调整。

图2 载机航迹与姿态Fig.2 Aircraft tracks and attitudes

采用图1中反演算法，在10 min 时间内，目标距离载机的距离R如图3（a）所示，光电转塔的方位角和俯仰角分别如图3（b）和3（c）所示。

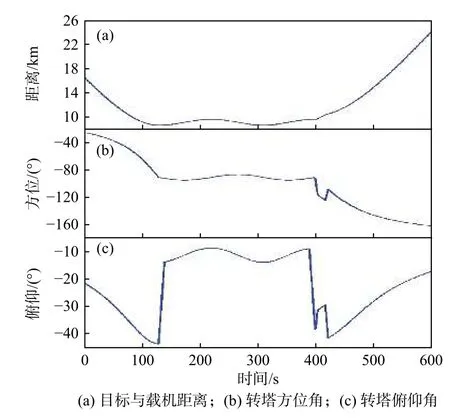
图3 反演结果Fig.3 Inversion results

3.3 误差源分析

依据第2 节和第3.1 节的分析，误差主要来自GPS 测量载机经纬高的误差、INS 测量载机姿态的误差、光电转塔视轴稳定精度带来的误差、目标横向与纵向像素偏差角的视频判别误差、测距机测量误差等。上述误差，可以看成许多量的叠加，根据中心极值定理，从统计意义上讲是满足Gaussian分布的随机误差，其大小如表1所示。此外，还存在GPS、INS 和光电转塔的安装误差，在载机结构刚性假设下，这三者是固有误差，可通过地面校轴加以减小，本文暂不列入分析。对于传感器视场角和分辨率，也可通过地面检验进行测量，本文暂将其列为固定值。

3.4 有源目标定位

当目标与载机距离用测距机测量得到时，采用图1中有源目标定位算法，计算得到的目标经度、纬度和高度分别如图4（a）、4（b）和4（c）所示。其中蓝色曲线是10 min 内单点有源定位直接结果，绿色曲线是上述直接结果在1 s 内做均值滤波得到，红色直线代表目标真实位置。从结果中可以看到：1）经度、纬度和高度直接定位结果的最大-最小误差分别为0.001 304°、0.001 630°、64.119 4 m；2）做1 s 滤波后，经度、纬度和高度定位结果的最大-最小误差分别为0.000 093°、0.000 118°、5.083 5 m；3）目标定位的经纬高是概率收敛到其真实位置。

表1 误差源及其大小Table1 Error source and its intensity

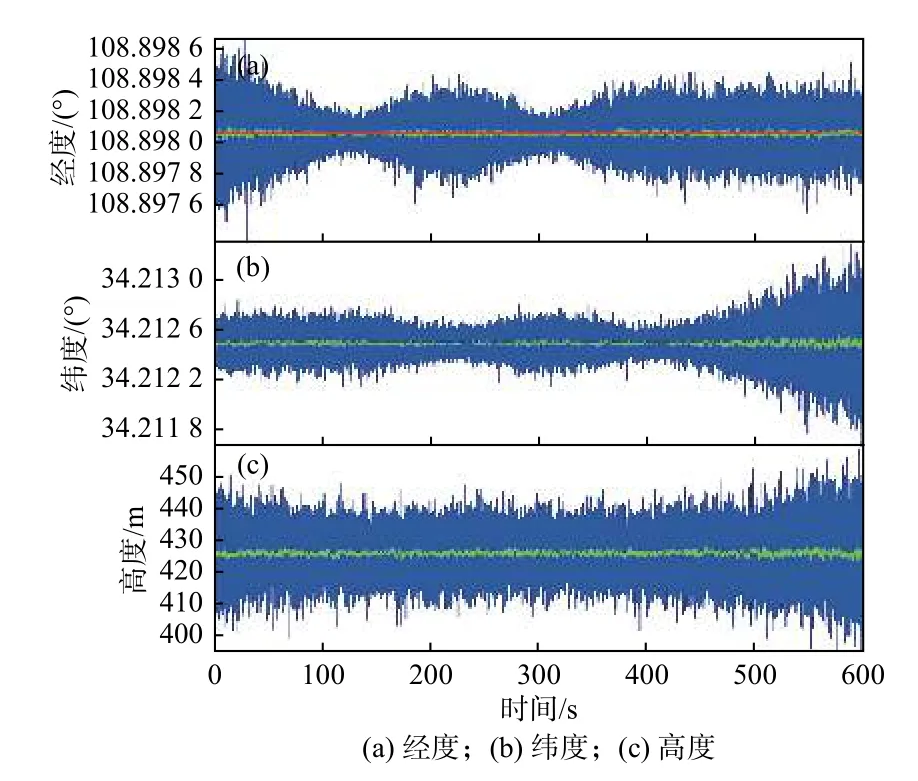
图4 有源目标定位结果Fig.4 Active target location results

3.5 无源目标定位

由于单点无源目标定位理论所限，其要求目标位于海平面上，即假设第3.2 节中目标的高度为0，接着，类似第3.2 节反演过程计算光电转塔的视轴，然后对加入噪声的观测量采用图1中无源目标定位算法，计算得到目标经度、纬度，分别如图5（a）、5（b）所示，目标定位位置与真实位置之间的距离如图5（c）所示。其中蓝色曲线是10 min 内单点无源定位直接结果，绿色曲线是上述直接结果在1 s 内做均值滤波得到的，图5（a）、5（b）中红色直线代表目标真实位置。从结果中可以看到：1）经度、纬度直接定位结果的最大-最小误差分别为0.002 466°、0.001 966°；2）做1 s 滤波后，经度、纬度定位结果的最大-最小误差分别为0.000 170°、0.000 139°；3）目标定位位置与真实位置之间的距离1 s 均值滤波前后分别为129.969 7 m 和44.495 5 m；4）目标无源定位结果比有源定位结果差。

图5 无源目标定位结果Fig.5 Passive target location results

4 目标定位精度分析

4.1 Monte-Carlo 方法

蒙特卡洛（Monte-Carlo）方法亦称为随机模拟（random simulation）方法，有时也称作随机抽样（random sampling）技术或统计试验（statistical testing）方法。该方法是先建立一个概率模型或随机过程，然后通过对模型或过程的抽样试验来计算统计特征，最后给出所求解的近似值[15]。概率论中的大数定律和中心极限定理是蒙特卡洛方法的理论基础。

4.2 圆概率误差仿真

目标定位的圆概率误差定义为：以目标真实位置为圆心划一圆圈，若定位点位于圆圈内的概率为P，圆圈的半径为r，则称定位结果在P置信度下的CEP 半径为r。

假设载机在（东经108°58′，北纬34°5′，高度6 000 m），姿态水平，光电转塔方位北偏西30°，俯仰水平向下20°，像素偏差为0，传感器视场及分辨率同前文，各误差源的大小同表1，采用无源定位算法，设定1 000 次样本实验，结果如图6所示。图中，红色圆圈代表目标真实位置，此时目标距离载机17.606 km，绿色和蓝色十字代表1000 次无源定位计算得到的目标位置，其中绿色十字代表接近目标真实位置占比80%的定位结果，其半径为39.404 m，亦即CEP 半径=39.404 m@80%置信度，最差定位结果与目标真实位置相距80.463 m。

图6 无源目标定位蒙特卡洛分析结果Fig.6 Passive target location results by Monte-Carlo analysis

4.3 统计直方图仿真

假设载机在（东经108°58′，北纬34°5′），载机高度范围[1 000，8 000]，航向范围（-180，180]，俯仰范围[-45，45]，横滚范围[-45，45]，转塔方位范围（-180，180]，俯仰范围[-75，-15]，其他参数同前。限定目标至载机的距离在20 km 内为合理取值，选取1 000 个样本点，则有810 个样本的载机-目标距离在合理范围，其分布如图7（a）所示。目标推算位置与真实位置的距离落于80%范围内的半径最小值为8.59 m，最大值为117.82 m，其大多数情况位于40 m 内，位于30 m 内有726 个样本，占有效样本数的89.63%，其分布如图7（b）所示。目标推算位置与真实位置的距离最大半径最小值为18.25 m，最大值为372.28 m，其大多数情况位于100 m 内，其分布如图7（c）所示。

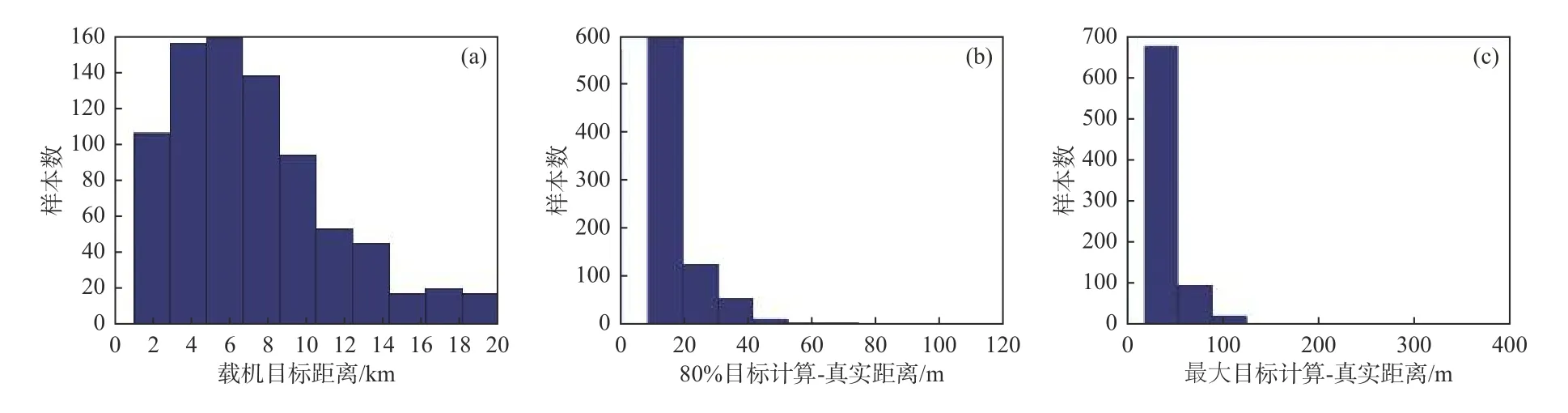
图7 统计直方图分析结果Fig.7 Analysis results of statistical histogram

5 结论

本文对于光电目标定位从理论到仿真进行了研究：首先分析了目标定位中用到的坐标系及其相互转换关系，然后给出光电转塔视轴反演、有源目标定位、无源目标定位的算法流程，接着通过仿真实验加以验证，其间考虑了定位过程中可能的随机误差来源，并分析了是否采用均值滤波对定位结果的影响，最后通过Monte-Carlo 分析计算了定位精度。通过给定条件的仿真实验，得到以下结论：1）有源定位比无源定位的精度高（精度约提高1 倍）；2）均值滤波后，定位精度有较大提升（约提高15 倍）；3）约18 km 距离典型无源定位精度在80%置信度条件下约为39.4 m；4）载机高度、姿态、转塔视轴等在一定范围内采样统计，限定目标载机距离在20 km 内为合理取值，其80%置信度CEP 半径从8.59 m～117.82 m，最大误差为18.25 m～372.28m。