基于利萨如图形及关联度分析的高压输电电缆护层故障识别研究

赵威，夏向阳，李明德，潘志敏，雷云飞，刘卫东，张静

(1. 长沙理工大学电气与信息工程学院，湖南长沙，410114；2. 衡阳市产商品质量监督检验所，湖南衡阳，421000；3. 国网湖南省电力有限公司检修公司，湖南长沙，410000)

电缆是电力运输的载体。交联聚乙烯电缆由于具备良好的电气特性被广泛应用于大中城市输电网络构建[1]。但随着运行时间增加，受外力损毁、绝缘层腐蚀、非正常运行等因素影响，电缆故障率逐年提高，可靠性逐渐降低，成为破坏电网安全运行的重大隐患[2]，其中，中高压电缆护层、接头、连接箱和终端等连接部位是故障高发部位[3-4]。当前电缆护层故障在线监测及识别方法趋于完善，所获取的参数多样化，已不局限于绝缘介质损耗角、局放电流、接地线环流等参数[5-7]。现有分析方法以数值比值法居多，但判断阈值的设定主观性较大，且未对数据充分挖掘[8-10]。目前的研究方法集中于对常用的特征提取算法和智能分类算法进行多种组合(即信号分析与模式识别的组合)实现对电缆故障的诊断识别。ZHONG等[11]同时利用堆叠自动编码器与S变换相结合进行故障识别。ZONG 等[12]采集小波奇异值以量化故障特征，结合支持向量机实现故障识别。黄健民等[13]利用小波变换获取电流信号小波熵，通过阈值诊断实现电缆故障识别。PANG等[14]对信号进行小波分解获取小波奇异值，然后采用改进SMOTE算法在少数类的样本中心邻域进行插值再抽样处理，利用优化分类器进行线路故障识别。姚海燕等[15]结合小波变换与灰色关联分析方法，通过计算灰色关联度来识别电缆早期故障。邵宝珠等[16]将非负约束自动编码器堆叠形成的深度学习网络应用于电缆故障识别中。上述研究主要对电缆早期故障和绝缘状态进行评估，对具有复杂护层回路的交叉互联电缆故障研究较少。赵威等[17]利用轨迹法对交叉互联高压电缆中环流信号进行实时在线特征提取，获取椭圆特征参数进行在线监测，但只对故障特征参数变化情况进行了分析，并未涉及采用何种优化方法实现故障识别。高压交叉互联电缆回路复杂，监测参数规律性不明显且故障类型和故障点较多。关联度法能很好地处理数值及规律性较复杂的样本，计算相对简单，适应性和通用性强，适用于高压交叉互联电缆故障识别。本文在文献[17]的基础上，将基于利萨如图形的信号分析方法和基于关联度的模式识别方法相结合，通过构建利萨如图形长轴长度、短轴长度、离心率、倾斜角为元素的输入特征向量，求解未知故障类型的输入特征向量与已知故障类型参数组成的样本空间向量的熵、熵权、关联系数等得到关联度，最终实现故障识别，并通过实例分析验证该方法的准确性，以期为高压电缆故障识别提供新思路。

1 高压电缆利萨如图形分析

1.1 高压电缆接地系统电流分析

一段电缆可看作无数个绝缘等效二端口的级联，如图1 所示。图1 中：Im为护层环流；Zi为绝缘层阻抗，泄漏电流Ii从线芯经主绝缘流至金属护层；IC为电容电流，其在金属护层中分别从左右两侧流入接地点，对应分量分别为IL和IR；ZmL为该电缆护层左侧各段对地等效阻抗的矢量和；ZmR为该电缆护层右侧各段对地等效阻抗的矢量和；I1和I2为电缆护层接地箱处的接地线电流。

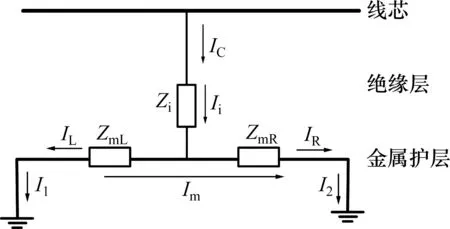
图1 护层回路电流Fig.1 Current in shield circuit

当电缆发生故障时，Im，IL，Ii和IR均会发生变化，因此，可通过测量分析电缆护层中的电流对电缆故障或绝缘状态进行监测。由于采用交叉互联接地的电缆在测量时电流传感器仅能安装于接地同轴电缆，Im，IL，Ii和IR难以直接测取，因此，选择采集接地线电流I1和I2并加以分析。以下通过等效电路图结合接线图对接地线电流、护层环流、电容电流进行分析。由于泄漏电流通常很小，因此，本文忽略其影响，不单独计算。图2所示为一段交叉互联电缆护层等效电路图，将实际工程中的分布式参数简化为集总参数。

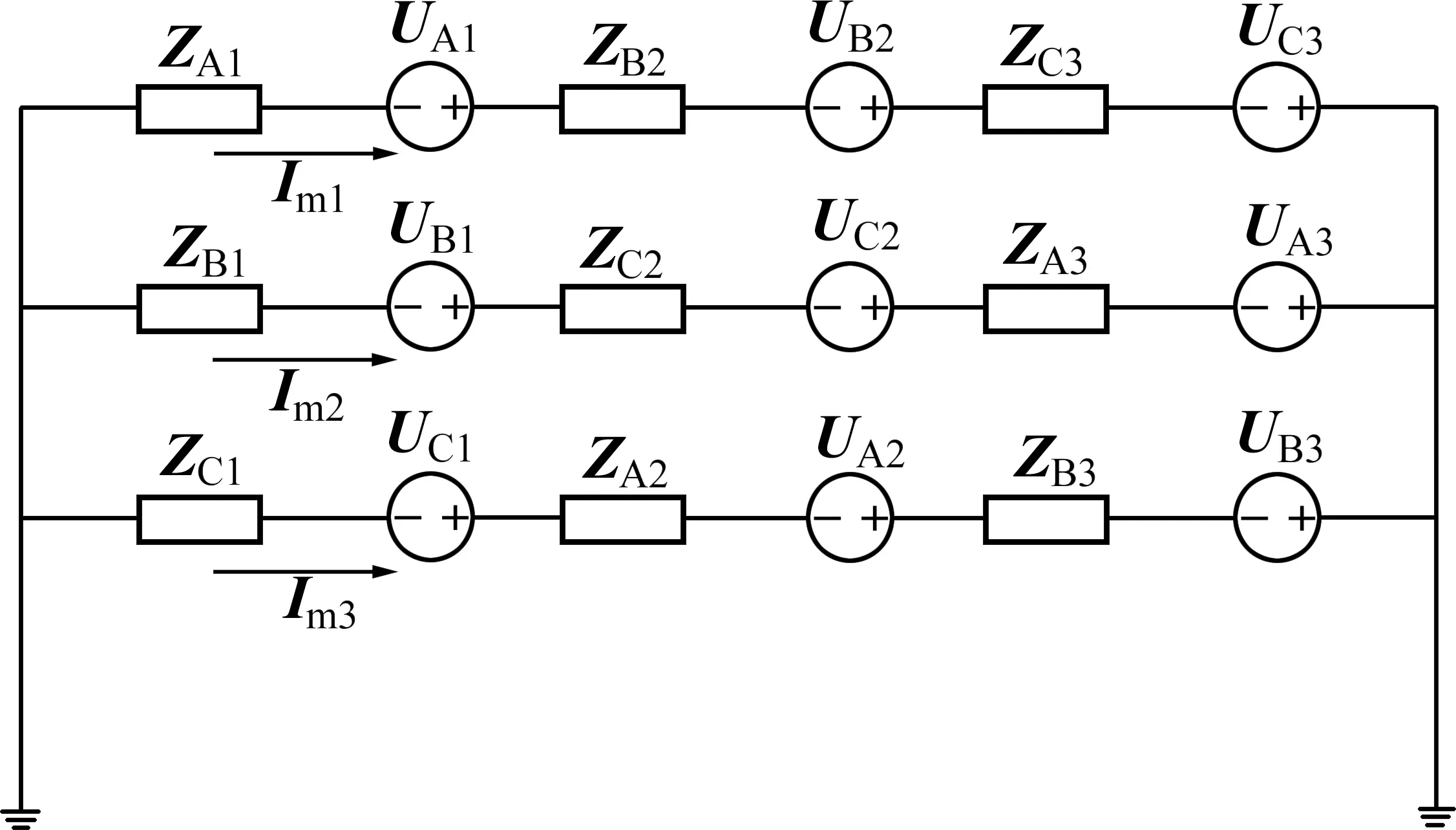
图2 护层等效电路图Fig.2 Sheath equivalent circuit diagram

图2中，Uni(n为A，B和C，i为1，2和3，下同)表示各段电缆产生的感应电压和互感电压的等效值，Zni为各段电缆自阻抗，Imi为各护层电流。三段护层电流计算式为

电容电流计算式为：

式中：ωC为各段电缆的电容导纳；U为电缆运行电压。由图1 知电容电流在护层中分为两部分流动，向左及向右流动的2个电容电流分量计算式分别为

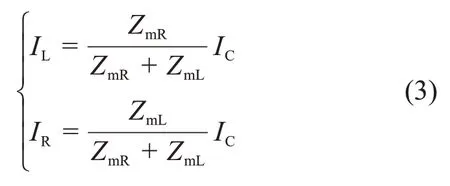
1.2 接地线电流利萨如图形构建

基于前面分析，结合接地系统接线图对接地线电流变化情况进行分析。选择图2所示等效电路图中A1-B2-C3护层回路进行分析，如图3所示。

图3 护层接线图Fig.3 Sheath wiring diagram

图3 中：Im1为护层环流；InLi和InRi(n为A，B和C，i为1，2 和3)为电容电流在护层中的分量，I1a和I4c分别为两侧直接接地箱处A 相和C 相接地线电流。设流向为左、下的电流矢量为正，根据KCL 定理可计算两侧直接接地箱接地线电流，如下式所示：

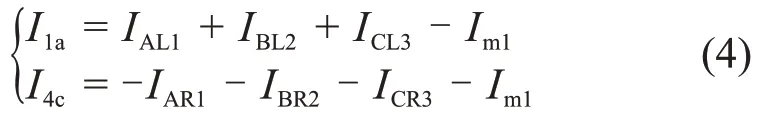
由公式(5)可知，I1a和I4c共同反映护层回路A1-B2-C3的运行状况。两电流分量通常可视为同频率分量，可在相同采样周期内采集其数据。

由图3可得如下数学关系式：

整理式(6)和(7)，提取ωt可得

去掉负数次方可得

根据微积分几何学原理，当式(8)无解、有2个相同解、2个不同解时，其图形分别为椭圆、抛物线、双曲线；当式(8)有相同解时，其图形为抛物线[18]。

根据求根公式从式(8)中提取下列求根因式：

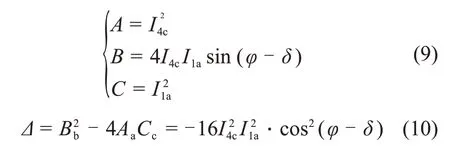
图4 利萨如图形Fig.4 Lissajous figure

等式(10)恒小于0，故式(8)所示图形为椭圆，投影至新的二维平面可得图4 所示利萨如图形(中图)。图4 中，I1a(t)(左侧直接接地箱处A相接地线电流)，I4c(t)(右侧直接接地箱处C相接地线电流)的进行变换，采集同一时间点上的数值投影至新的二维平面图4中几何形状为椭圆的利萨如图形。任何故障的发生或运行状态的改变均会改变图形的特征参数。

利萨如图形特征参数示意图如图5 所示。图5中，I1a为左侧直接接地线A相电流，I4c为右侧直接接地线C相电流。利萨如图形特征参数包括长轴长度a、短轴长度b、倾斜角e和离心率θ，分析这些特征参数的变化规律可实现对故障的识别和监测。

2 基于关联度的电缆护层故障识别方法

2.1 关联度定义

关联度的具体定义如下：设Xi表示系统一时间序列，在任意时刻n的对应数据为xi(n)(n=1,2,3,…,k)，其中k为时间序列中的最后一个采样时刻对应的采样点，则Xi=(xi(1),xi(2),xi(3), …,xi(n))为第i个因素Xi的特征行为序列。在实际应用中，序列可写为矩阵形式，n可为时间序号、对象序号或指标序号。当关联度法应用于电力设备故障诊断时，n通常为指标序号，xi(n)为设备第n种故障特征监测数据。

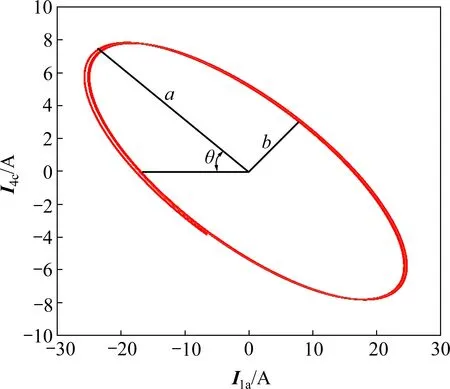
图5 利萨如图形特征参数示意图Fig.5 Characteristic parameter diagram of Lissajous figure

设系统m个对象的特征行为序列分别为X1，X2,X3,…,Xi(其中，i=1, 2, 3, …,m)。选择X0为参考序列，其余序列均为比较序列。

给定实数φi，有

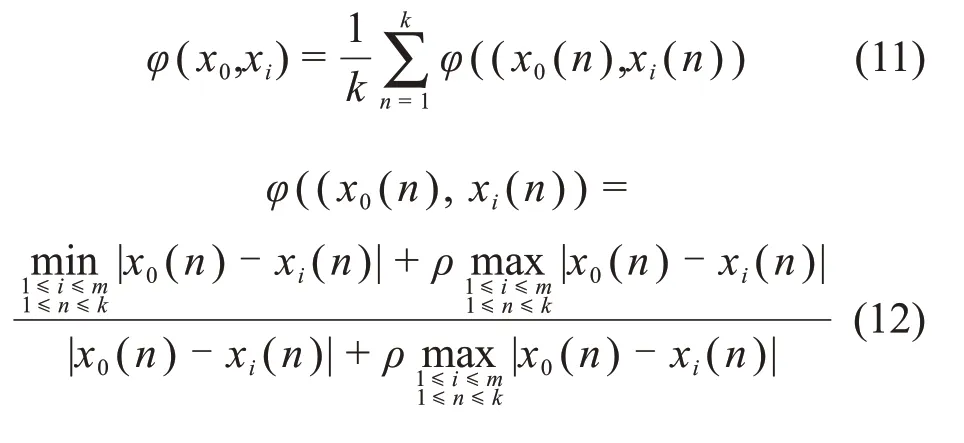
若式(12)满足规范性、整体性、偶对称性、接近性，则称φ((x0(n),xi(n))为xi(n)对x0(n)的关联系数，φ(x0,xi)为xi对x0的关联度。式(13)中，ρ为分辨系数，其作用是提高色关联度之间的差异显著性，取值范围为0～1，一般取0.5[19]。

关联度的具体计算过程如下。

1)选择参考序列x0(n)和比较序列xi(n)。

2) 求参考序列和比较序列之间的绝对差值序列:

3)求两级最小差和两级最大差：

4)求解关联系数与关联度。

2.2 基于关联度的电缆护层故障识别流程

本文利用构建的高压电缆环流利萨如图形所获得的特征参数包括长轴长度、短轴长度、离心率、倾斜角的变化率Δa，Δb，Δe，Δθ及2 组环流参数I1a和I4c共6个特征参数作为输入向量X。每个特征参数对应1 个评价指标，其中，Δa和Δb直接反映2组测量环流的变化，Δe体现2组环流比值上的差异，结合阻抗变化Δθ可反映2组环流间的电缆部分绝缘变化情况；I1a和I4c作为辅助参考依据。对于1个未知结果的输入向量，首先分析参数数值情况，依据故障大类判据确定故障类别，再根据包含具体故障信息的样本空间，通过计算关联系数等得到识别结果。输入向量(待测样本)为

同时，由ATP-EMTP 仿真及实地获取含正常运行、接头短路、接头击穿、护层绝缘破损、护层保护器击穿/进水、同轴电缆破损等故障的参考样本，形成6N维的样本空间矩阵X′：

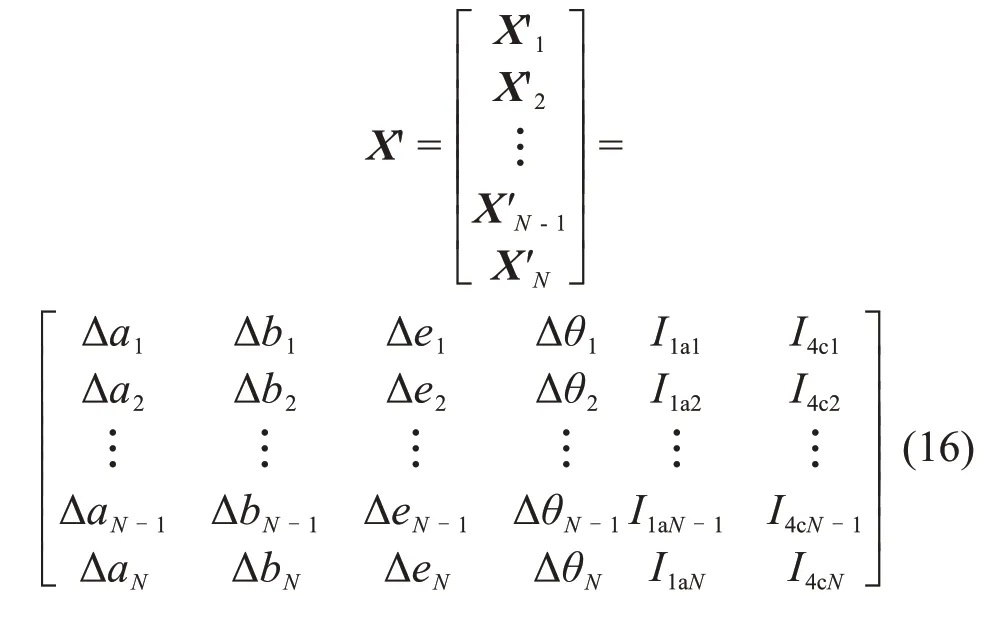
X′中各序列分别表示1种故障的特征参数。

由于6个参数变化差异较大，为“避免大数吃小数”的现象，首先将样本空间矩阵X'进行归化运算[20]，而后求解第k(k=1, 2, …, 6)个特征参数的熵与熵权，分别为：

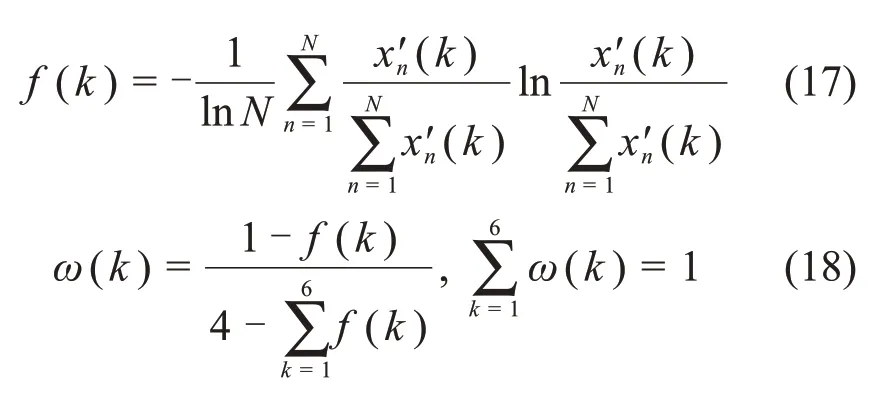
式中：f(k)为指标熵；ω(k)为权重系数；x'n(k)为参考样本X'n中第k个特征参数值。信息熵值法是根据各指标包含的信息量确定指标的权值，熵权与熵成反比，熵越小表示信息有效性高。由于不同高压电缆故障发生机理及破坏的结构不同，对各特征参数变化的影响程度存在差异，因而，利用熵权对特征参数进行赋权调整有助于提高故障识别正确率。熵权与熵成反比，熵越小表示信息有效性越高。由于不同高压电缆故障发生机理及破坏结构不同，对各特征参数变化的影响程度存在差异，因而，利用熵权对特征参数进行赋权调整有助于提高故障识别正确率。

X与X'n第k个指标的关联系数δn(k)如式(19)所示，再由关联系数矩阵结合各特征参数的熵权向量，通过式(20)得到X与X'n的总关联度ψn。

关联度ψn越大，则待测样本X与样本空间中对应样本X'n相关程度越大，其中，关联度最高的1 项所对应故障情况即为待测样本的故障识别结果。

由上述分析所得识别模型整体思路如图6 所示。首先将故障数据按故障大类进行区分，随后求取包含具体故障点的小类故障空间的关联度，以便于减小计算量。参考样本中包含的故障类型如图7所示，包括同轴电缆破损、接头松动、外护套破损等故障。本文主要针对一段交叉互联高压电缆的外护套、接头、接地箱故障进行研究，构建相应样本空间。

图6 故障识别流程Fig.6 Fault identification

3 仿真与实例分析

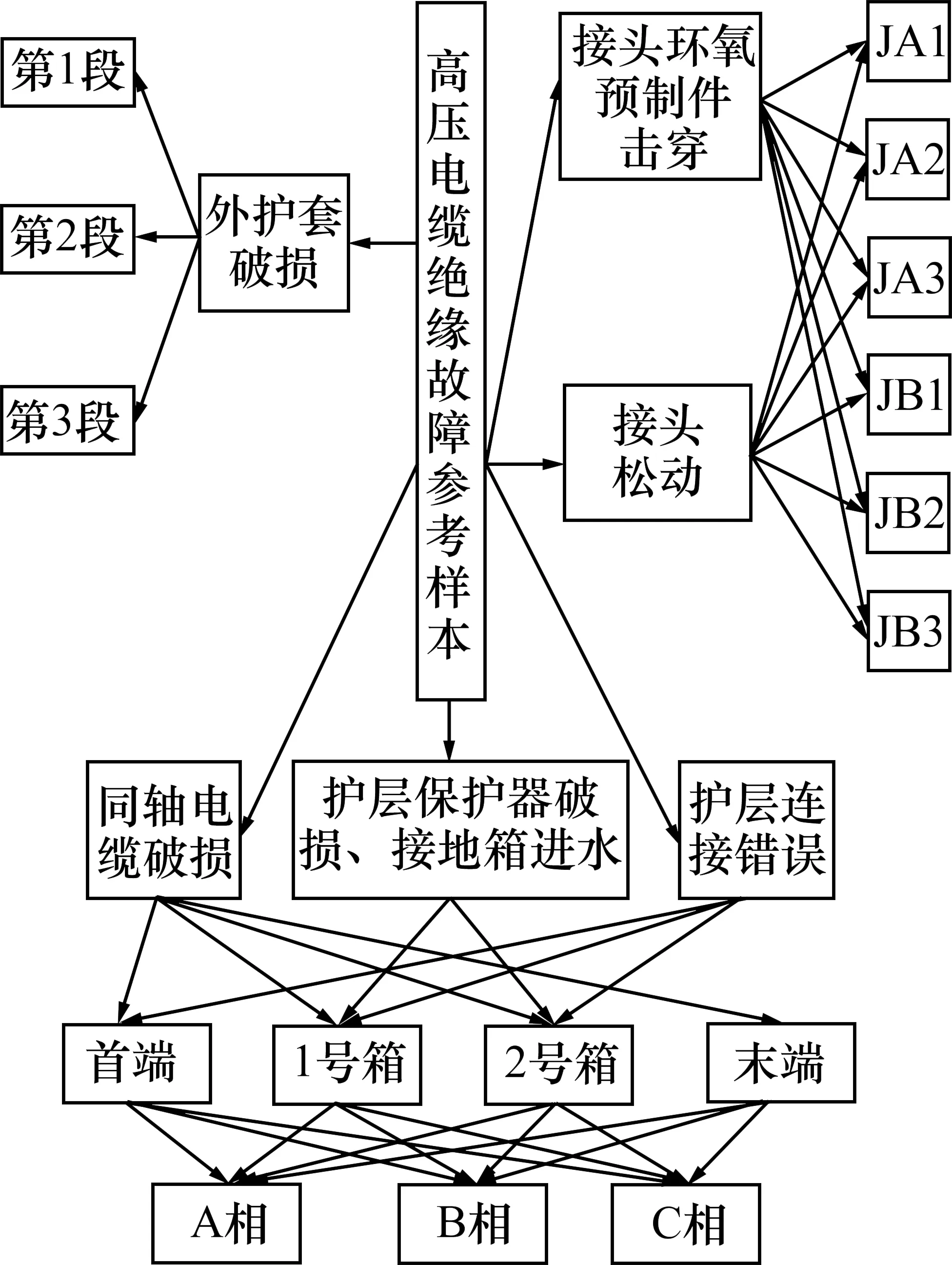
图7 参考样本故障类型Fig.7 Fault type contained in sample space

利用ATP-EMTP 建立一段长度为1 500 m、电压为110 kV 的交叉互联电缆模型，参数见文献[17]，仿真模型如图8所示，由4个接地箱，3段等长度等参数电缆组成，接地电阻设为1 Ω。本文设IAB为AB处A 相接地电流，ICD为CD处C 相接地电流。通过构建图3中护层回路利萨图形来分析该段电缆故障，并获取表1所示故障类型判据，包含长轴长度变化率Δa，短轴长度变化率Δb，离心率变化率Δe，用于初步判断故障大类。由部分故障的特征参数变化情况构造的样本空间共12组，如表2所示。选取2 组待测数据进行验证计算，2 组数据的利萨如图形如图9所示。

由图9经数据计算得到2组参数对应的利萨如图形特征参数变化情况，如表3所示。

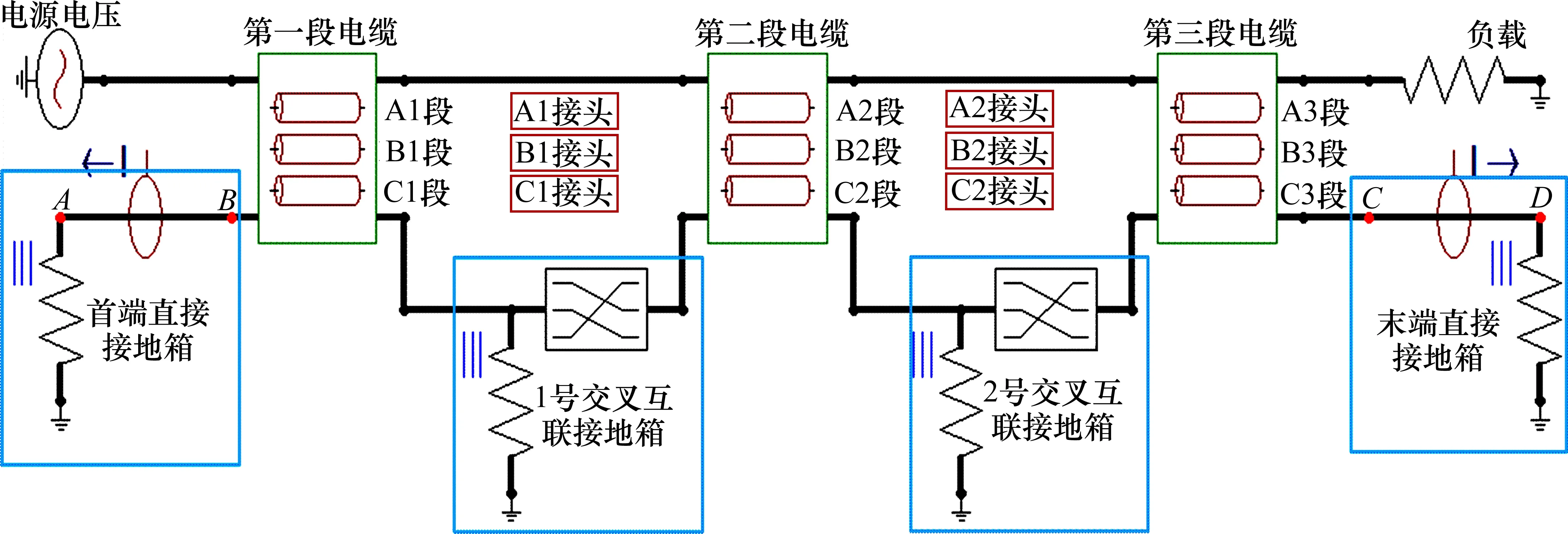
图8 仿真模型Fig.8 Simulation model

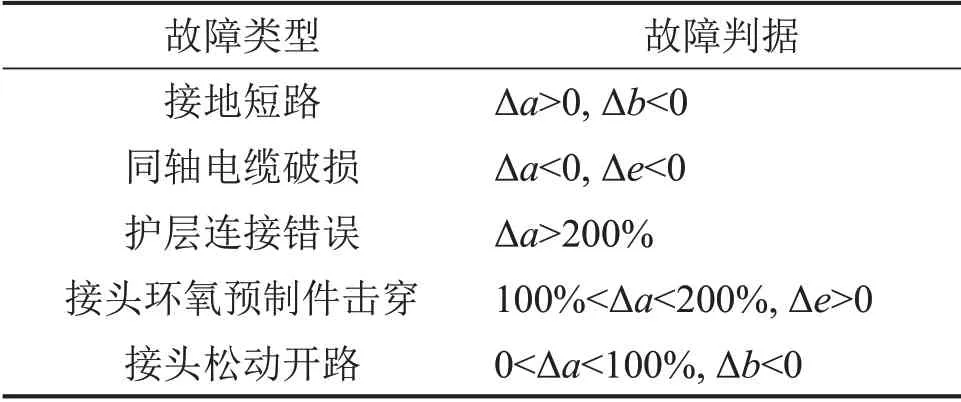
表1 利萨如图形故障判据Table 1 Lissajous figure fault criterion

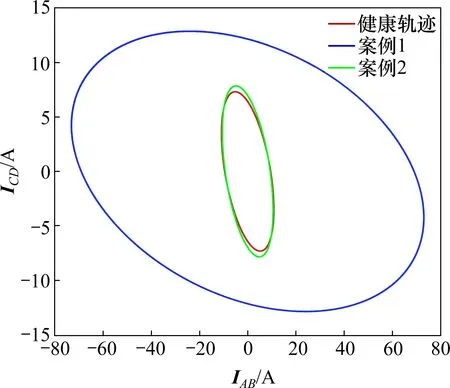
图9 待测故障利萨如图形Fig.9 Lissajous figure of unknown fault

表2 利萨如图形特征参数变化情况Table 2 Change of lissajous figure characteristic parameters

表3 待测数据利萨如图形特征参数Table 3 Unknown fault Lissajous figure characteristic parameters

由图9可见：案例1图形变化程度较大，案例2图形变化程度较小。使用关联度分析进行故障识别。案例1中，故障大类判据为1号箱护层连接错误，关联度计算结果分别为：A 相0.92，B 相0.67，三相0.78。案例2 中，故障大类判据为2 号箱同轴电缆破损，关联度计算结果分别为：A 相0.22，B相0.87，三相0.54。2组案例的识别故障均与预设故障一致。

经验证，某地某次发生故障环流录波数据如图10 所示。将采集的数据导入其中获取图形，计算特征参数变化情况见图10 中界面右侧，长轴长度变化率为30.8%，短轴长度变化率为-63.7%，离心率变化率为5.6%，倾斜角变化率为-4.36%。按图6所示流程进行故障识别。

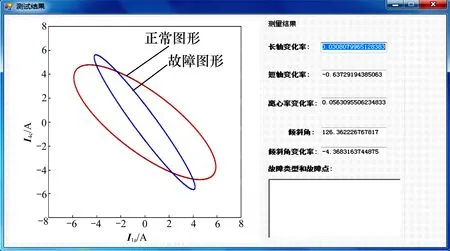
图10 上位机界面Fig.10 Host computer interface

故障判断为1号箱同轴电缆破损，关联度分别为：A 相0.93，B 相0.22，C 相0.54。根据规则认定为2号箱A相同轴电缆破损，经验证，识别结果与实际结果相同。由以上分析可见：利萨如图形的构建为高压电缆故障识别提供了更多参考信息，关联度分析的应用使故障识别结果更精准。

4 结论

1)提出了一种基于利萨如图形特征参数分析方法，结合关联度分析的高压电缆护层故障识别系统。建立了交叉互联电缆系统模型，对110 kV交叉互联电缆主段进行仿真，构建了高压电缆利萨如图形，获取了图形长轴长度、短轴长度、离心率、倾斜角的变化率。利萨如图形特征参数可有效分析高压电缆护层故障，并可作为故障类型及故障点的判据。

2)构建了利用利萨如图形特征参数作为输入向量的高压电缆护层故障关联度分析模型，利用仿真及实际数据组成参考样本空间，通过计算待测样本与样本空间各已知样本特征参数关联系数、特征参数熵权得到了待测样本与参考样本各序列之间的关联度。结合利萨如图形特征参数的关联度分析可用于高压电缆护层故障识别。

3)由于条件限制及电缆运行的特殊性，本文无法获取充足的实际故障样本进行研究，后续将在故障分类，故障判据的科学设定及关联度冲突处理上进行深入分析，并实现外护套破损的识别与定位。