可重复使用运载火箭一子级垂直回收有限时间滑模控制
2020-06-04李晓栋廖宇新廖俊罗世彬
李晓栋,廖宇新,廖俊,罗世彬
(中南大学航空航天学院,湖南长沙,410083)
可重复使用运载器(reusable launch vehicle,RLV)是指在完成发射任务后全部或部分返回着陆,经过检修维护和燃料加注后,可再次执行发射任务的一类运载器[1]。相对于一次性运载火箭而言,可重复使用运载火箭一子级(first-stage of reusable rocket,FRR)作为一类RLV,可通过多次执行助推和回收任务来降低火箭发射成本[2],因此,受到业界广泛关注。SpaceX 公司的“猎鹰-9”运载火箭成功进行了多次一子级垂直回收和复用飞行,掀起了业界对FRR 回收控制的研究热潮。由于FRR垂直回收过程空域大、速域广、飞行环境多变,使其本身多变量、非线性的系统又受到强烈的内外扰动和不确定性,这对控制系统的稳定性、鲁棒性和控制精度提出了更高的要求。面对如此复杂的非线性控制问题,一般的线性控制方法无法满足高精度、强鲁棒等控制需求。近年来,动态面控制[3]、自适应广义预测控制[4]、自适应反步控制[5]、滑模控制等非线性控制方法被应用于RLV飞行控制问题研究。其中,滑模控制对模型不确定和外部扰动具有较强的鲁棒性,被广泛应用于RLV 的再入姿态控制。与线性滑模控制的渐进稳定相比,终端滑模(terminal sliding mode,TSM)控制不仅使系统有限时间稳定,而且具有更强的抗干扰能力[6]。文献[7]针对高超声速飞行器再入姿态控制问题, 设计了终端滑模控制器(TSM controller,TSMC),保证系统有限时间趋于稳定,实现对期望值准确、快速的跟踪。文献[8]提出一种快速终端滑模控制器(fast TSMC,FTSMC),进一步减小了有限时间收敛上界。然而,TSMC 和FTSMC 都存在状态量的负指数项,可能会引发奇异性问题,导致系统在奇异区域输出的控制量趋于无穷大。文献[9]通过在奇异区域把终端滑模面切换成线性滑模面来避免奇异性。文献[10]通过设计非奇异快速终端滑模控制器(singularity-free FTSMC,SFTSMC),直接克服了控制器的奇异性问题。文献[11]提出的积分终端滑模控制器(integral TSMC, ITSMC)具有与SFTSMC 相似的特性,在消除奇异性的同时,保证系统有限时间稳定。传统滑模控制中符号函数的不连续切换特性所造成的控制不连续是引起抖振的根本原因。利用饱和函数代替符号函数来克服抖振的方法只能保证系统状态收敛到滑模面的邻域,降低滑模控制的鲁棒性和精度[12]。采用高阶滑模控制算法可以抑制抖振,但滑模面高阶导数信息要通过大量计算才能得到。文献[13]提出一种基于超螺旋算法(super-twisting algorithm,STA)的二阶滑模控制方法,不仅保持了高阶滑模控制能抑制抖振的优点,同时,无需对滑模面高阶求导。基于扩张状态观测器(extended state observer,ESO)的控制方法可以在保持控制性能的情况下消除模型不确定和外部扰动给系统带来的影响。文献[14]考虑模型不确定和外界干扰对FRR 的影响,设计固定时间ESO(fixed-time ESO,FxTESO)与SFTSMC 相结合的控制方法,实现对姿态角期望值的固定时间跟踪控制。文献[15]将滑模动态面控制技术和自适应滑模观测器技术结合,提出一种内外环自适应滑模动态面控制方法,使受到外部干扰的FRR 能够对姿态角指令进行准确跟踪,但该方法仅仅保证闭环系统渐进稳定。文献[16]提出一种FRR自适应容错控制方法,设计基于FxTESO的SFTSMC,不仅能处理外部扰动和模型不确定对系统的影响,而且当执行机构发生故障时也能使系统保持稳定。本文提出一种基于FTESO 和改进超螺旋算法(modified STA,MSTA)的积分终端滑模控制方法来解决FRR垂直回收无动力减速段姿态控制问题。采用FTESO 对系统不可测量状态量和总扰动进行估计,进一步将状态量估计值引入积分终端滑模面,同时,基于总扰动估计值和MSTA 设计改进超螺旋积分终端滑模控制器(modified supertwisting ITSMC,MSTITSMC),消除了传统终端滑模控制的奇异性,并有效抑制了抖振。本文首先在FRR 绕质心运动方程基础上引入跟踪误差变量,建立姿态控制模型;然后,设计FTESO 和MSTITSMC,进一步证明闭环系统有限时间稳定;最后,通过数值仿真验证所提出的控制方法的有效性和优越性。
1 数学模型及问题描述
1.1 绕质心运动方程
FRR的飞行剖面[17]如图1所示。本文考虑在无动力减速段的姿态控制问题。此阶段FRR 在大气层内飞行且推力为0 N,其速度减小和姿态变化主要是受到气动力和气动力矩的作用。假设FRR 是具有轴对称结构的刚体,体轴构成的坐标平面均为对称平面,其绕质心运动方程[14]为
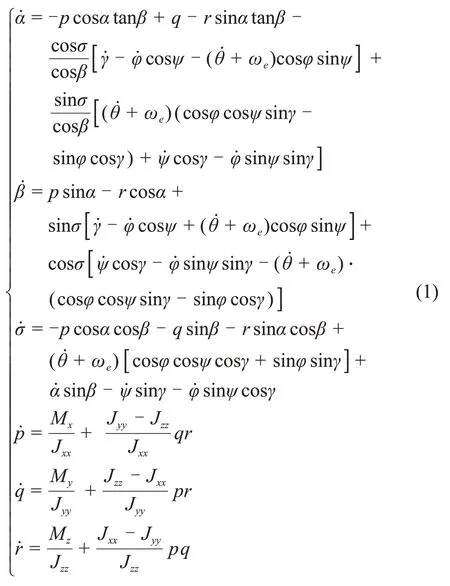
式中:α,β和σ分别为攻角、侧滑角和倾侧角;γ,ψ,φ和θ分别为航迹倾角、航迹偏角、经度、纬度;p,q和r分别为滚转、俯仰和偏航角速率;Mx,My和Mz分别为滚转、俯仰和偏航力矩;ωe=7.292 115×10-5rad/s,为地球自转角速度;Jxx,Jyy和Jzz分别为沿x,y和z轴转动惯量。
1.2 面向控制的模型及问题描述
定义Ω=[α,β,σ]T,ω=[p,q,r]T,考虑模型不确定和外界干扰,则绕质心运动方程(1)可进一步描述为
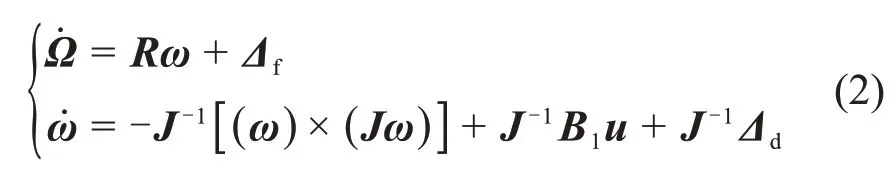
式中:Δf为表征模型不确定项变量;Δd为外部干扰;“×”为叉乘运算;u=[δa,δe,δr]T,为控制输入;δa,δe和δr分别为控制滚转、俯仰和偏航的等效舵偏角;J为惯性矩阵,
坐标转换矩阵R的具体表达式为
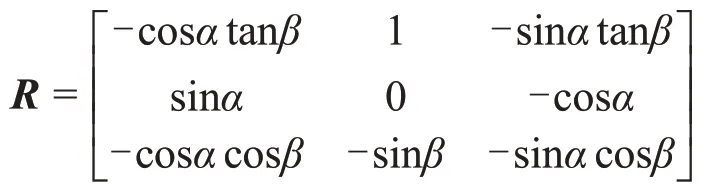
控制力矩矩阵B1[14]的具体表达式为
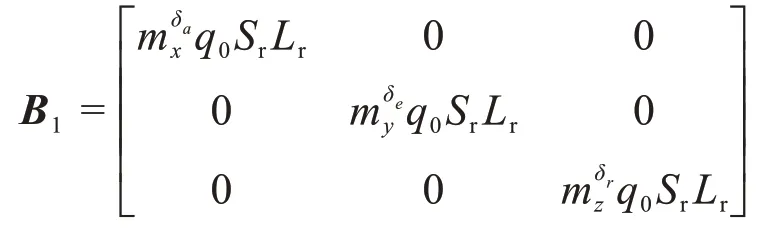
式中:和分别为滚转舵、俯仰舵和偏航舵的控制力矩系数;q0=0.5ρv2为动压;v为速度;ρ=ρ0e-h/7110,为大气密度;e 为自然常数;h为飞行高度;ρ0=1.225 kg/m3,为海平面大气密度;Sr和Lr分别为FRR的参考面积和参考长度。
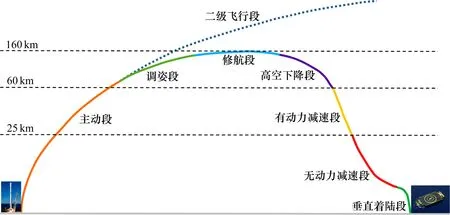
图1 FRR飞行剖面Fig.1 Flight profile of FRR
定义姿态角期望值Ωc、姿态角跟踪误差e1=Ω-Ωc和角速率跟踪误差结合式(2)建立二阶姿态跟踪误差系统为
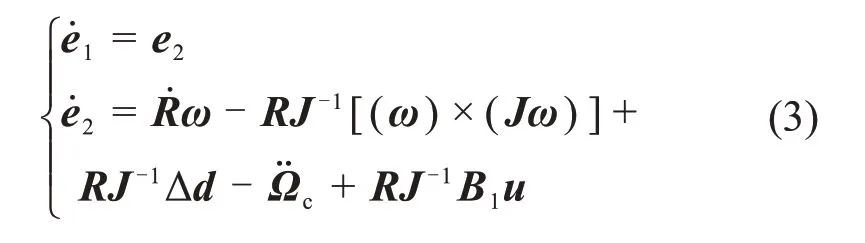
为了方便控制器设计,定义B=RJ-1B1,Δ1=为总扰动,则式(3)简化为
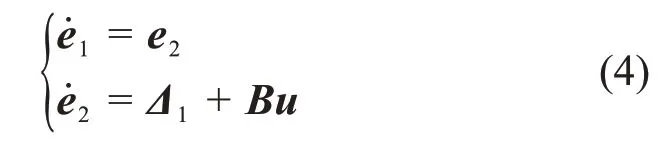
本文的主要目的是针对含有总扰动的二阶系统(4)设计控制器,使姿态跟踪误差e1和e2有限时间收敛。
2 基于FTESO 和MSTA 的积分终端滑模控制方法
FRR姿态控制系统结构如图2所示,主要包括FTESO 和MSTITSMC 两部分。首先,基于姿态角跟踪误差e1和控制输入u设计FTESO,得到角速率跟踪误差及总扰动的估计值;然后,基于观测器估计值和姿态角跟踪误差e1设计MSTITSMC,实现对期望值的高精度快速跟踪。
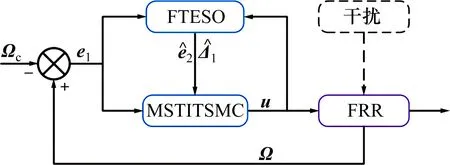
图2 FRR姿态控制系统结构Fig.2 Structure of FRR attitude tracking control system
2.1 定义与引理
定义1 对于向量x=[x1,…,xn]T有如下定义:

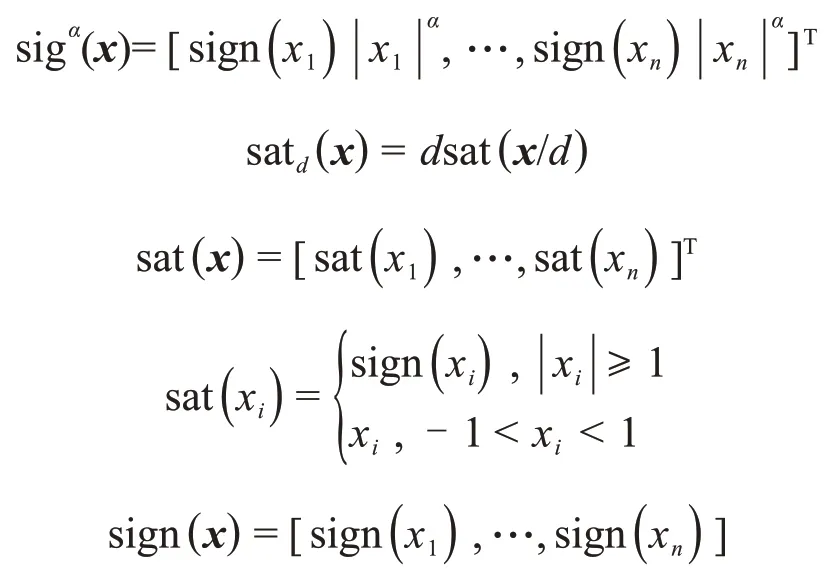
式中:sign(xi)为符号函数。
引理1[18]对于非线性系统,x∈Rn,假设V(x)是定义在U∈Rn的光滑正定函数。 若 存 在 正 常 数λ和μ∈(0,1) 使 不 等 式V˙≤-λV μ,x∈U{0}成立,则该系统是有限时间稳定的,收敛时间T满足
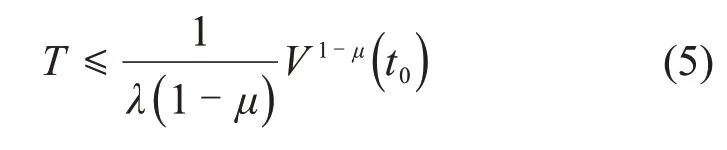
式中:V(t0)为V的初值。
引理2[19]考虑以下二阶系统:
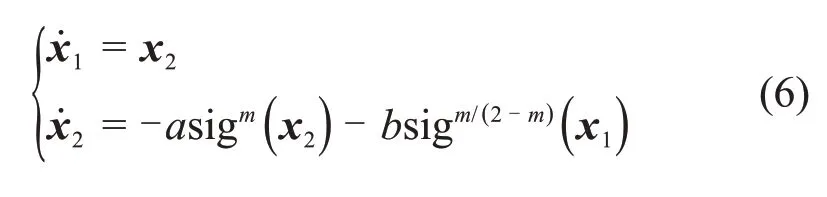
若0<m<1,a和b是使r2+ar+b为Hurwitz 多项式的正常数,则上述系统是有限时间稳定的。
2.2 有限时间扩张状态观测器
假设1总扰动Δ1及其导数有界,即且满足=g(Δ1)。
在以上基础上,将式(4)增广为
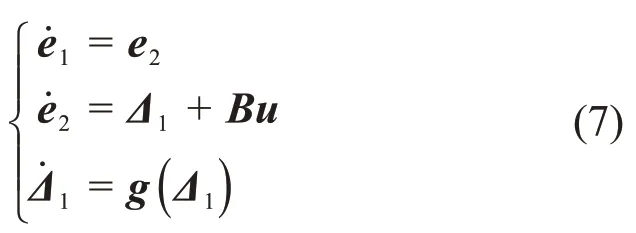
定义和分别为e1,e2和Δ1的估计值,针对系统(7)设计FTESO为
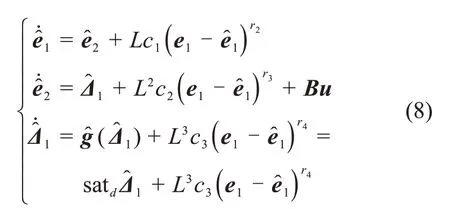
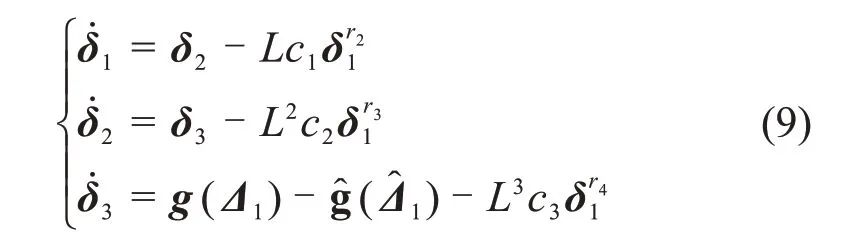
定义εi=δi/Li-1,i= 1,2,3,则式(9)可表示为

由文献[20]定理1可知,系统(10)的状态ε1,ε2和ε3将在有限时间内收敛,即利用FTESO(8)可以在有限时间Te精确估计e1,e2和Δ1。
2.3 改进超螺旋积分终端滑模控制器
设计积分终端滑模面为
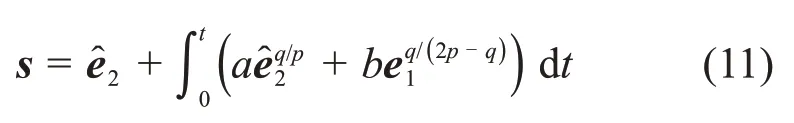
式中:p和q均为正奇数且p>q;a和b是使r2+ar+b为Hurwitz多项式的正常数。
基于MSTA[21]设计趋近律为
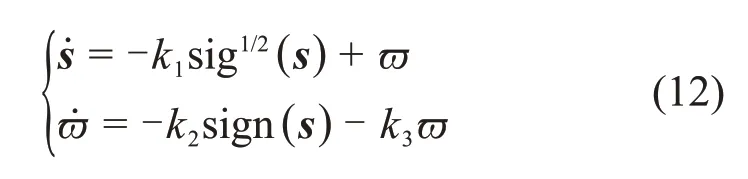
式 中:s=[s1,s2,s3]T;ϖ=[ϖ1,ϖ2,ϖ3]T;k1>0,
k2>0,k3>0。
结合式(11)和式(12),设计MSTITSMC为
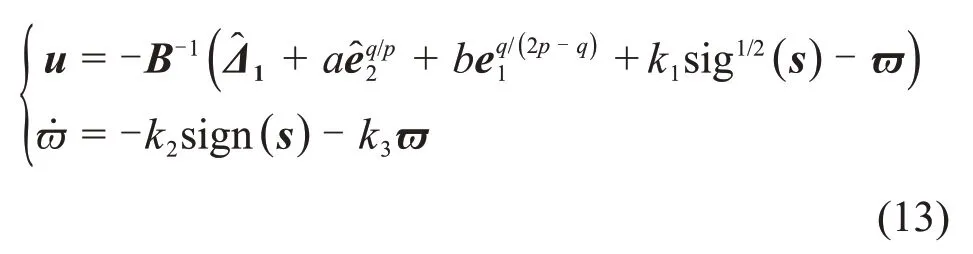
注1:在传统SMC 的滑模面中引入非线性积分项,构成积分终端滑模控制面,在保持传统SMC 优点的同时,避免了控制器奇异性问题,且保证系统状态在滑动阶段有限时间收敛。
注2:相较于标准STA[13]及其他MSTA[22],本文使用的MSTA通过在ϖ˙的动态方程中增加1个关于ϖ的线性项,即引入1 个与自身状态相关的反馈,调节了高阶项的动态响应。根据MSTA 设计的趋近律,不仅能抑制抖振,而且能保证系统状态有限时间收敛。
2.4 稳定性分析
定理1对于二阶系统(4),采用所设计的FTESO(8)和MSTITSMC(13),能够使闭环系统有限时间稳定,即保证姿态跟踪误差e1和e2有限时间收敛。
证明定理1 的证明可分3 步。第1 步证明在FTESO 有限时间收敛过程中,e1和e2有限时间有界;第2 步证明FTESO 收敛后,e1和e2能在有限时间收敛至滑模面,第3 步证明收敛至滑模面后,e1和e2能沿滑模面有限时间收敛至平衡点。
Step 1 对滑模面s求导,得

将式(13)代入式(4)可将闭环系统表示为
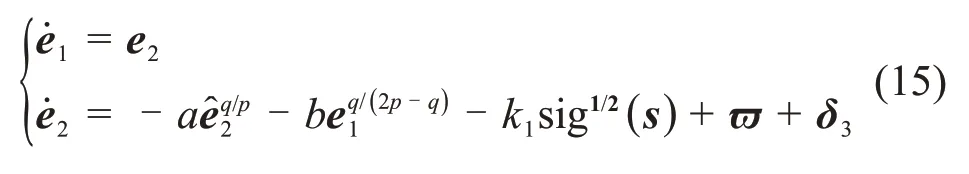
选取Lyapunov函数:
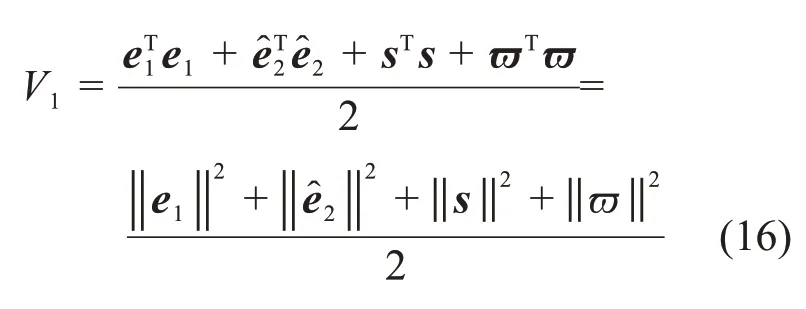
对V1求导,得

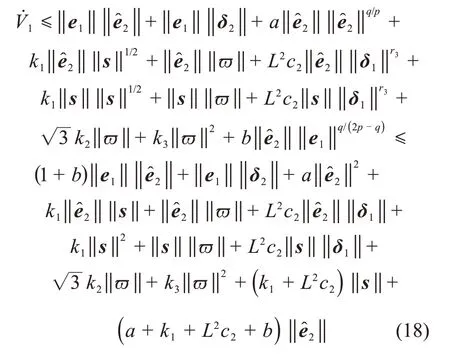
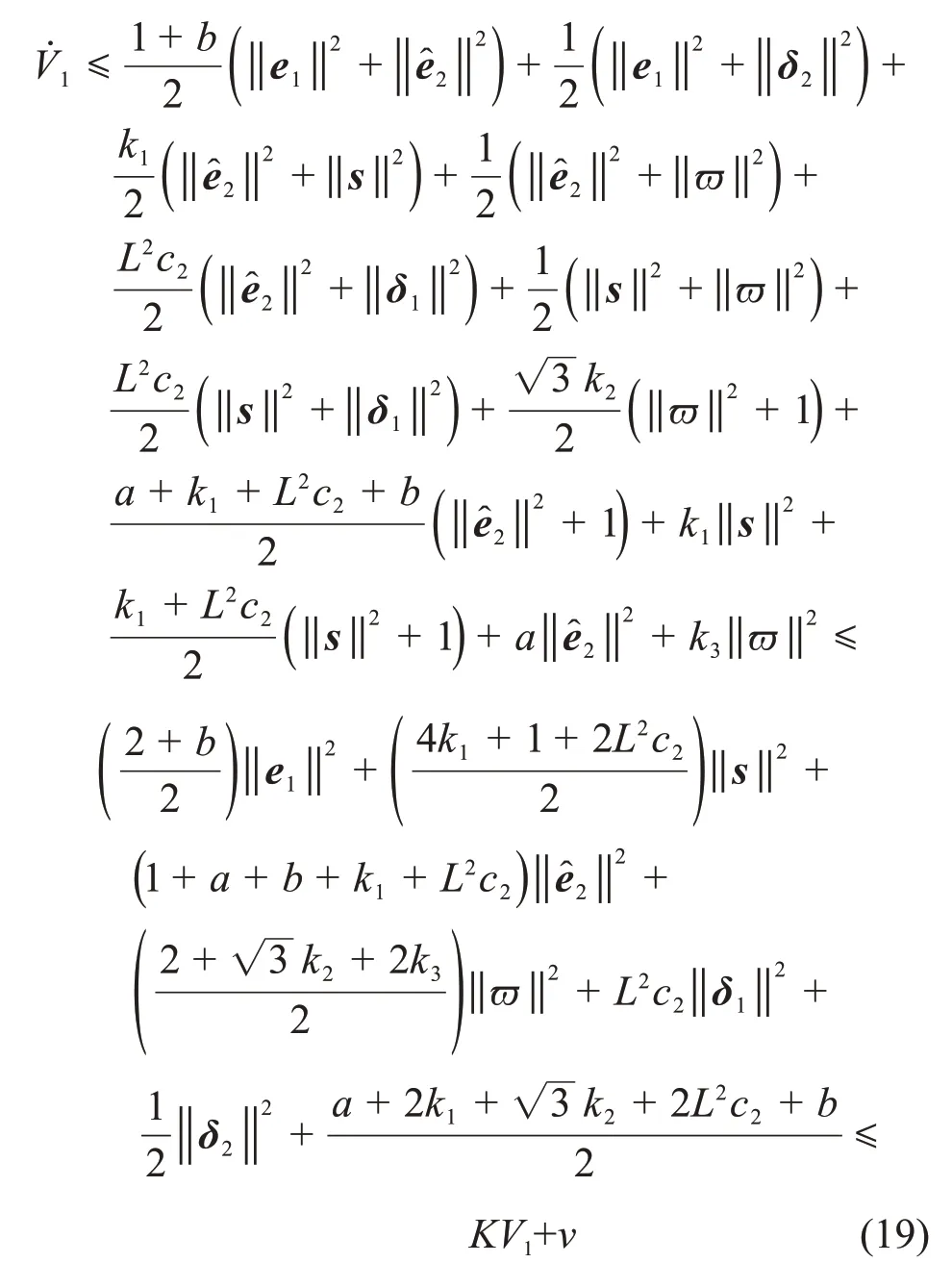
式中:
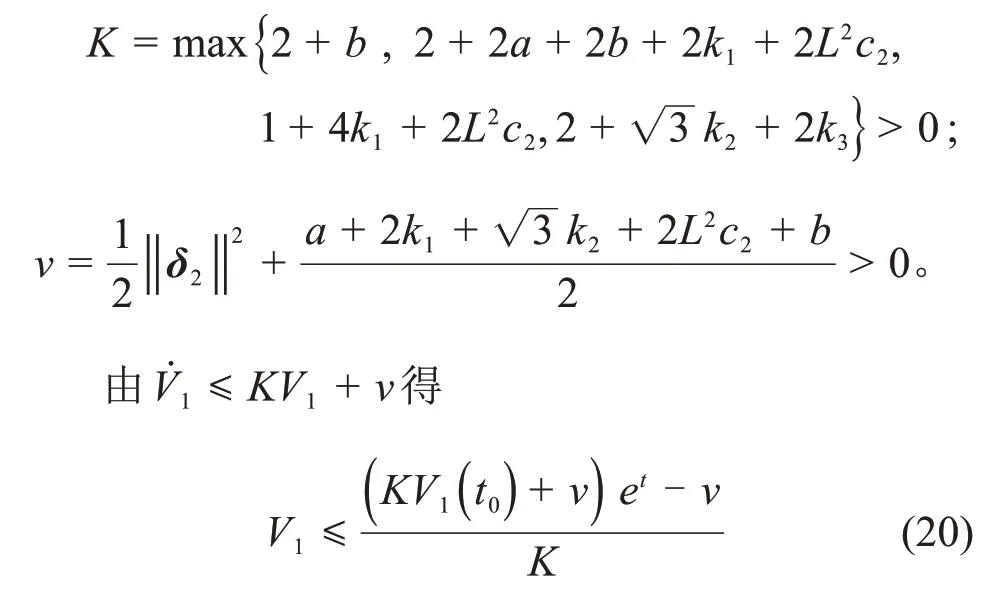
式中:V1(t0)为V1的初值。由于V1仅与时间t相关,显然V1在有限时间内有界,所以,e1和e2在有限时间内有界。
Step 2 当FTESO 有限时间Te收敛后,滑模面(11)可进一步表示为
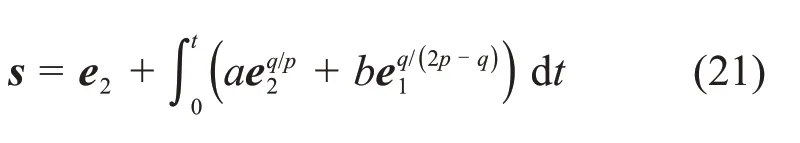
系统(15)可进一步表示为
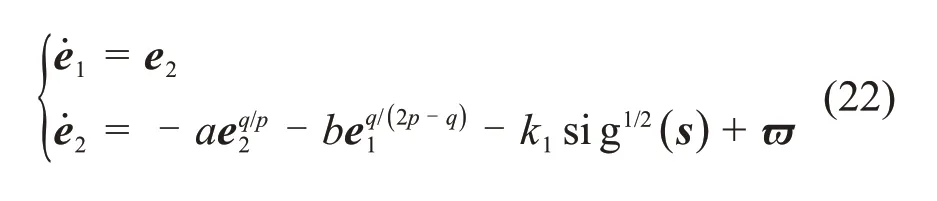
公允地说,现在的中学教材比几十年前好多了,既有传统文化,也有现代思潮;既有新闻实事,也有美妙畅想;既有铁肩道义,也有小我温情,可谓中西合璧,古今交融,兼收并蓄。教材内有人生选择,有风格个性,也有生命状态;有文学原典,有历史烟云,更有哲学思辨,几乎包含了整个人文世界。因此,相较于其他学段,中学应该更关注对教材“人文性”的挖掘。
xi=[xi1,xi2]T=[sig1/2(si),ϖi]T,i= 1, 2, 3。
对xi求导,得
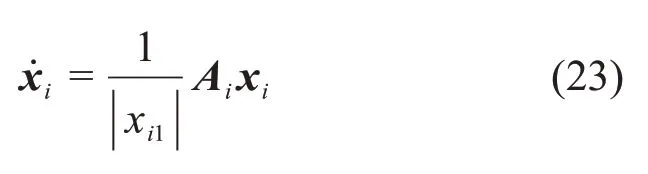
选取Lyapunov函数:
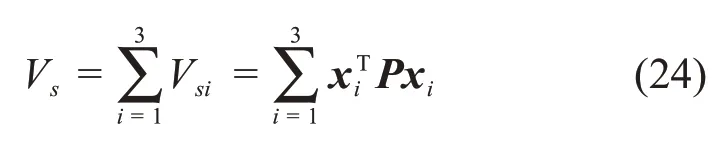
对Vs求导,得
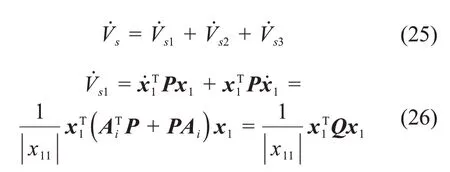
式中:
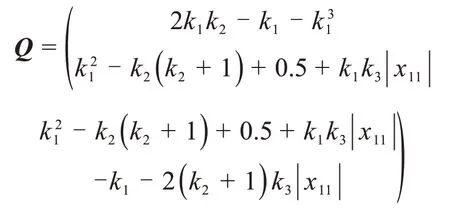

式中:
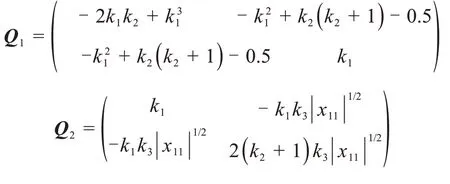
为了保证矩阵Q1和Q2正定,需要满足以下不等式:
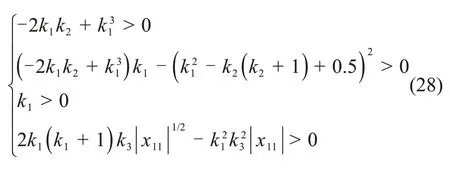
定义矩阵Q的最小特征值为λmin(Q),考虑不等式式(27)可表示为
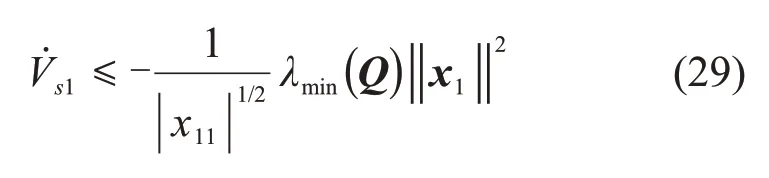
定义矩阵P最小特征值和最大的特征值分别为λmin(P)和λmax(P),考虑不等式和则式(29)可表示为

式中:
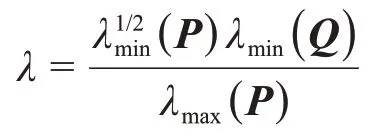
同理可证:若式(28)和不等式
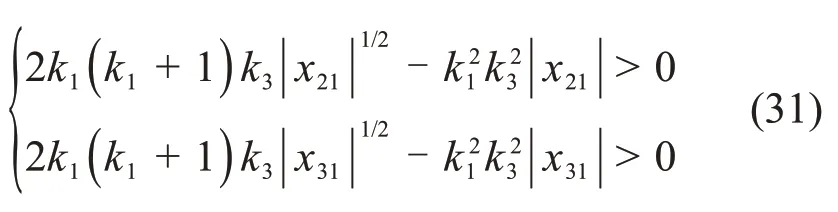
由此可知,满足以下关系式:
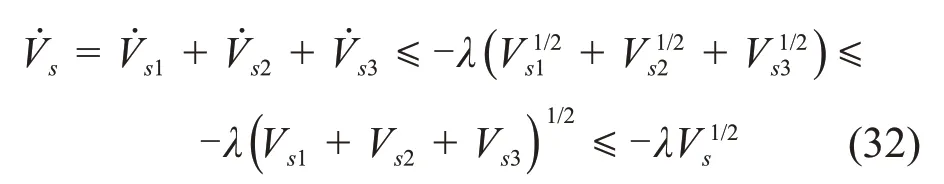
由引理1 可知,若参数k1,k2和k3同时满足式(28)和式(31),则当t≥Ts时,有且Ts满 足其 中Vs(Te)为Vs在Te时的值。
Step 3 当e1和e2收敛至滑模面时,系统(22)可进一步表示为
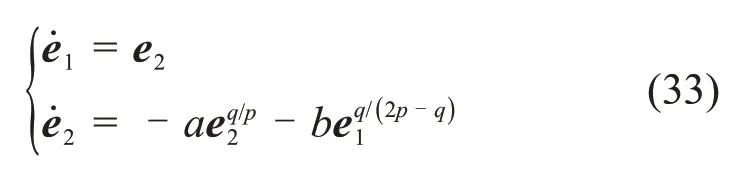
由引理2 可知,上述系统在有限时间内稳定,即e1和e2在有限时间内收敛。
定理1证毕。
3 数值仿真与分析
为验证所设计FTESO+MSTITSMC 方法的有效性,将其与文献[10]提出的SFTSMC方法、文献[14]提出的FxTESO+SFTSMC 方法在MATLAB/Simulink中的数值仿真结果进行对比。
仿真中,FRR的相关参数来源于文献[14];初始姿态角为Ω0=[-17,-0.573,-1.146]T(°);初始角速率为ω0=[-8.239 7×10-4,-0.005 3,-1.596 9×10-4]T(°)/s;绕质心运动方程中含有描述质心运动的6个时变状态量,可通过对质心运动方程数值积分得到。为完成仿真,设置状态量的初值为φ0=-47°,ψ0=0°,γ0=-41°,θ0=-47.15°,v0=1 180 m/s,h0=25 000 m;姿态角期望值Ωc=[5t/30-5,2t/30-1,0]T(°);气动系数偏差、转动惯量偏差和大气密度偏差为+20%,质量偏差为100 kg;所受扰动力矩为Δd=104[1+sin(πt/2+π/6),1+sin(πt/2+π/3)]TN·m;等效舵偏角限制在[-30°,30°];仿真步长为5 ms,仿真时长为30 s。
本文设计的方法FTESO 参数设置为L=5,d=4,c1=c2=10,c3=12,MSTITSMC 参数 设 置 为a=15,b=50,p=13,q=11,k1=0.70,k2=0.10,k3=0.01。对比的2种方法参数设置与文献[10]和[14]中的一致。
图3~5 所示为FRR 姿态角跟踪曲线。从图3~5 可见:与FxTESO+SFTSMC 方法相比,本文设计的方法能在更短时间对姿态角期望值实现稳定跟踪,在动态响应过程中的超调量也更小,而无观测器的SFTSMC 方法姿态角跟踪误差较大,在跟踪倾侧角期望值时发生了明显偏离。
图6~8 所示为等效舵偏响应曲线。从图6~8可见:FxTESO+SFTSMC 方法的等效俯仰舵偏δe在0.2~0.3 s 到约束上界,其余2 种方法输出的舵偏响应均在合理幅值范围内。
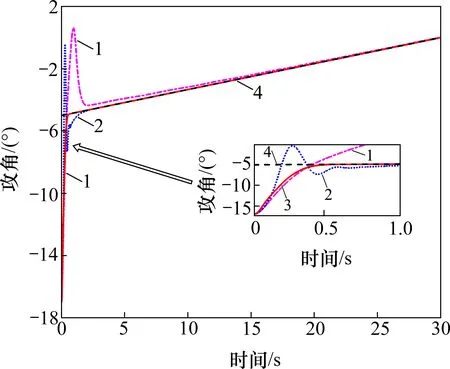
图3 攻角跟踪曲线Fig.3 Tracking curves of attack angle
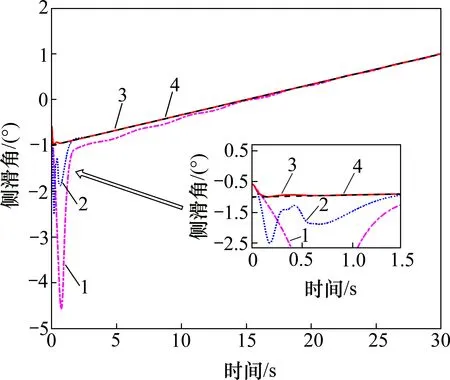
图4 侧滑角跟踪曲线Fig.4 Tracking curves of sideslip angle
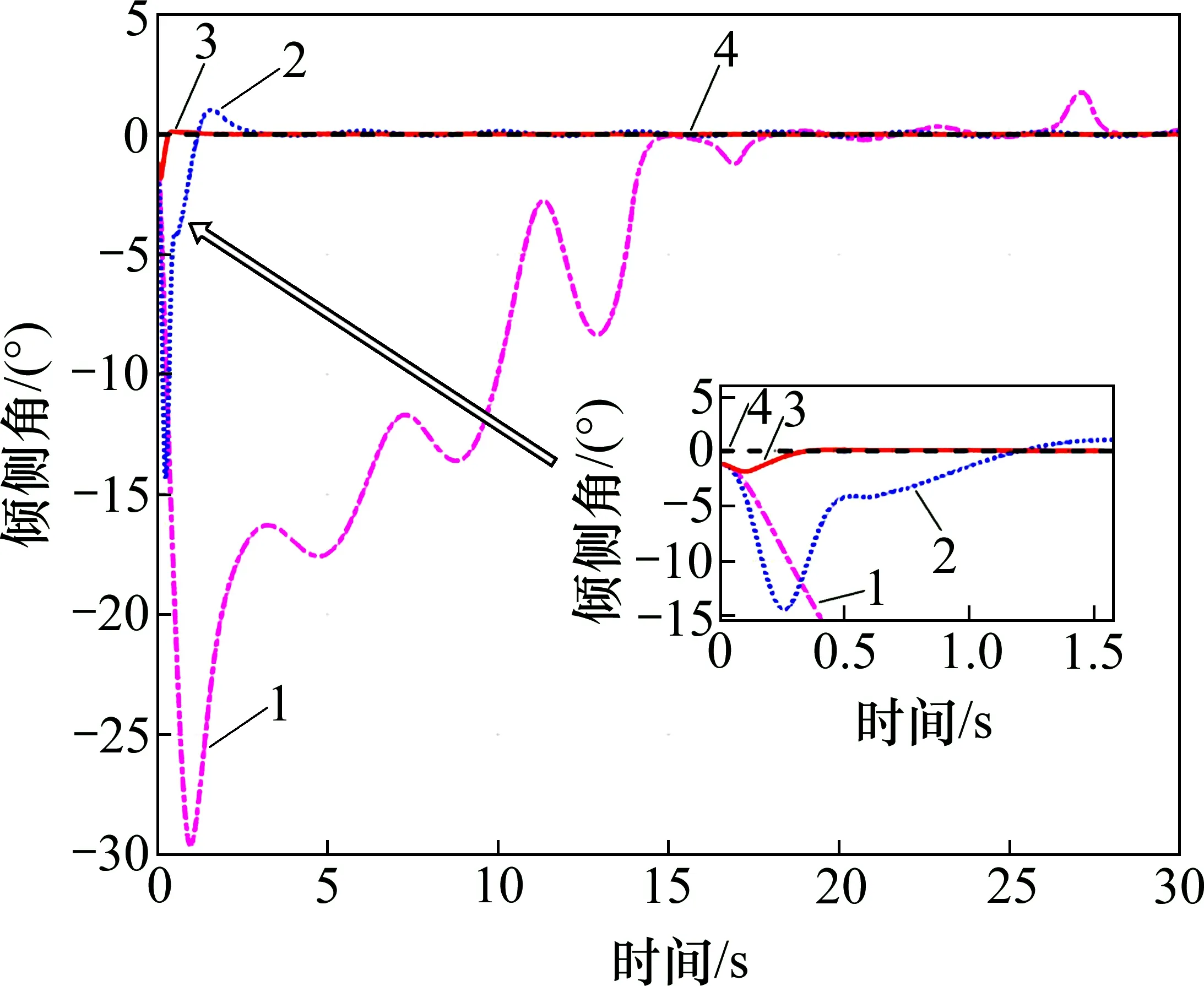
图5 倾侧角跟踪曲线Fig.5 Tracking curves of bank angle
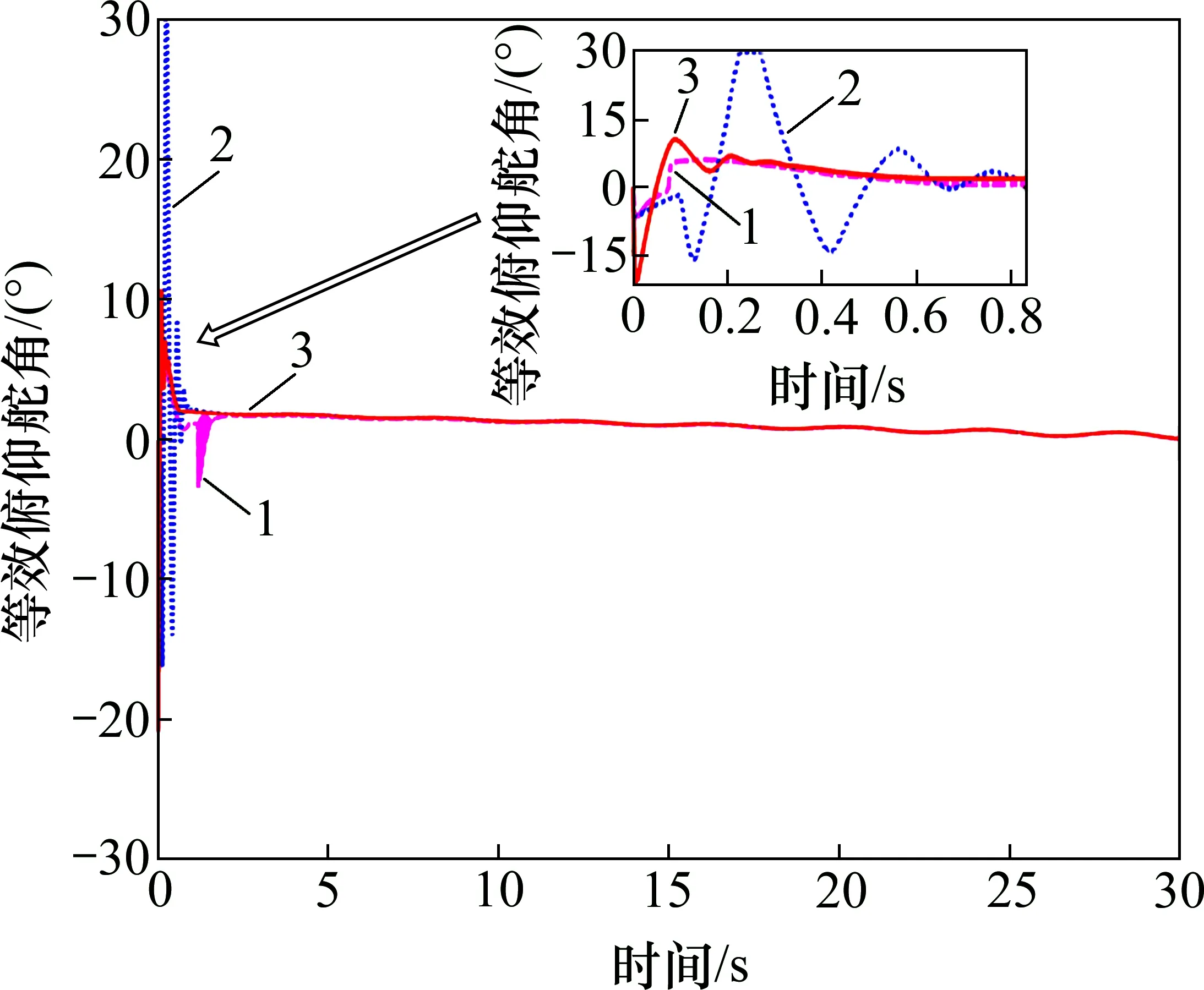
图6 等效俯仰舵角曲线Fig.6 Curves of equivalent pitch rudder angle
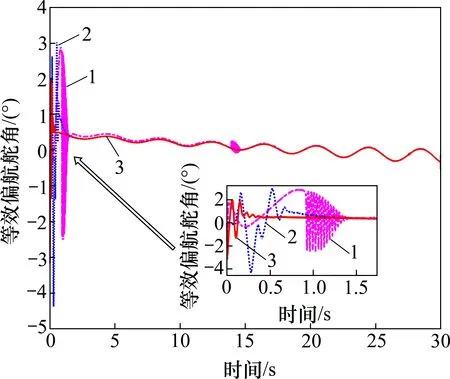
图7 等效偏航舵角曲线Fig.7 Curves of equivalent yaw rudder angle
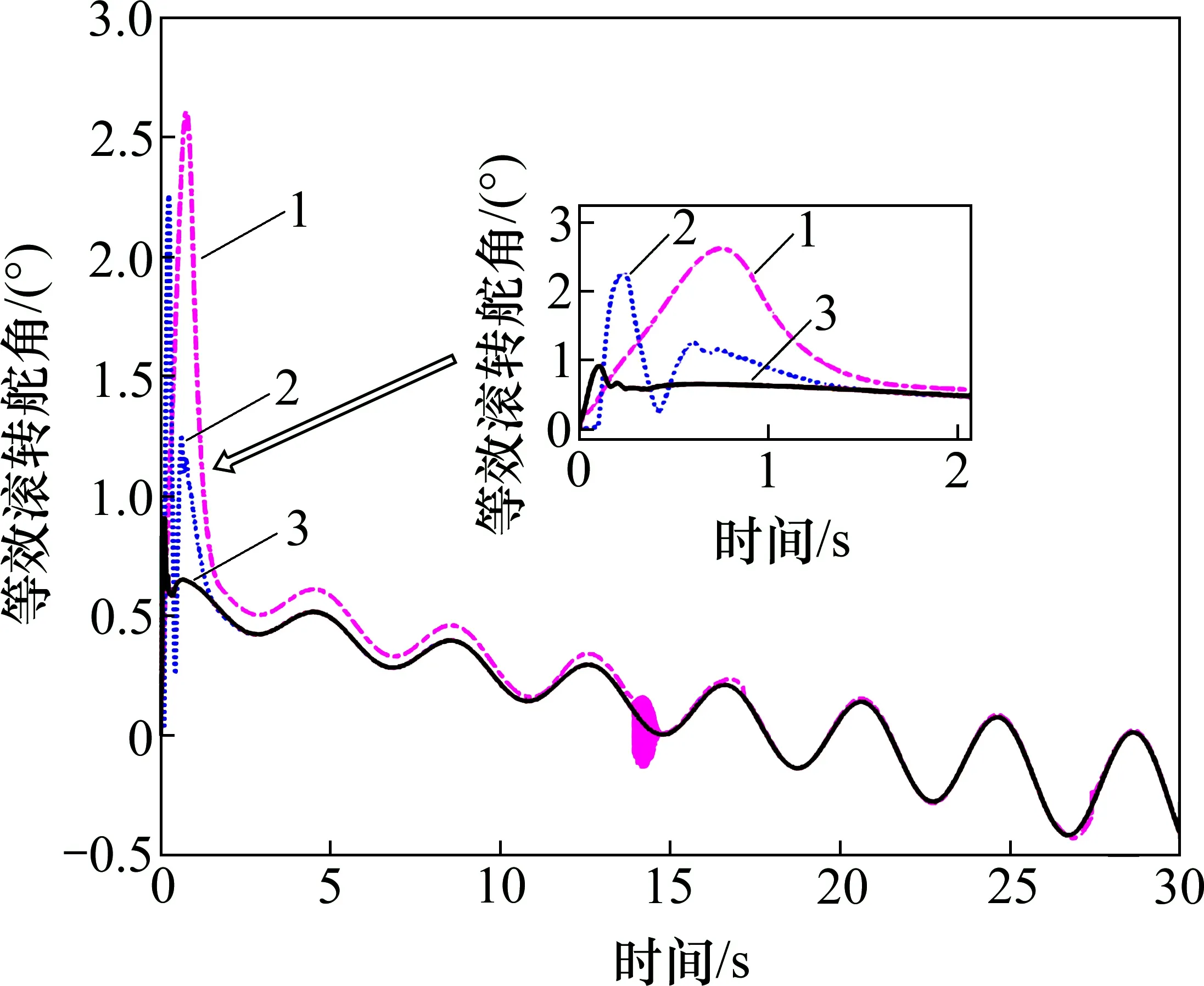
图8 等效滚转舵角曲线Fig.8 Curves of equivalent roll rudder angle
图9所示为滑模面的变化曲线。从图9可以看出本文设计的方法对应的滑模面s1,s2和s3分别在1.0,0.5和1.5 s左右收敛,且收敛过程较平滑,无明显抖振。综上所述,本文设计的FTESO+MSTITSMC 方法能准确、快速地跟踪姿态角期望值,且对扰动有较好抑制效果。
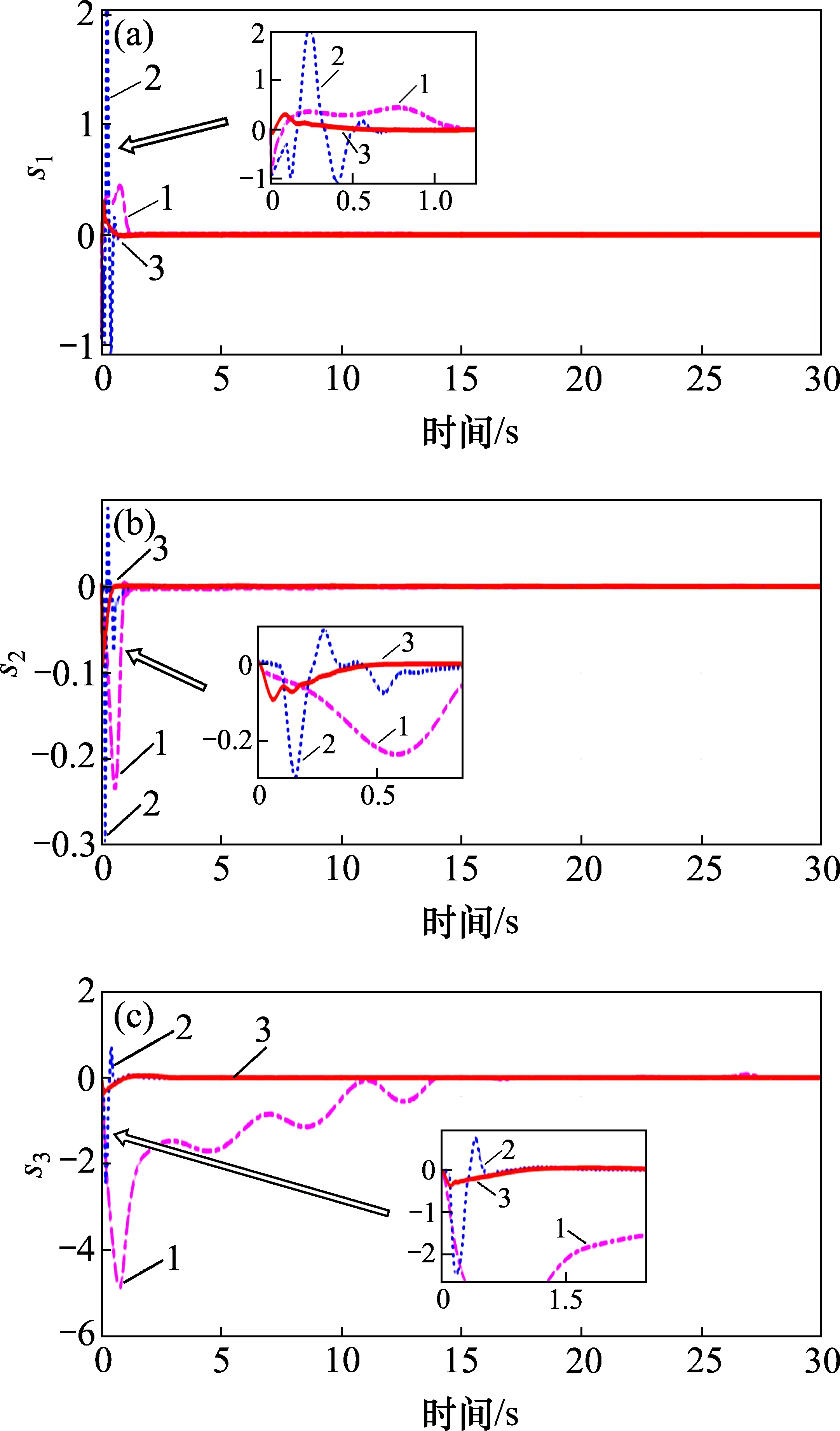
图9 滑模面曲线Fig.9 Curves of sliding mode variable
4 结论
1)针对FRR 垂直回收过程无动力减速段存在模型不确定和外部扰动等情况,提出一种基于FTESO 和MSTA 的积分终端滑控制方法。采用FTESO 对姿态角速度和总扰动进行估计,将角速度估计值引入积分终端滑模面,同时,基于总扰动估计值和MSTA设计了MSTITSMC。
2)基于Lyapunov 理论证明了闭环系统有限时间稳定;将本文设计的方法与2种非奇异快速终端滑模控制方法进行仿真对比,发现本文设计的方法对模型不确定和外部扰动具有较强鲁棒性,能对姿态角期望值进行准确和快速跟踪。
