基于有限单元法的裂纹梁结构疲劳寿命预测模型

2020-06-04龙慧刘义伦李松柏

中南大学学报（自然科学版） 2020年4期

龙慧，刘义伦，李松柏

(1. 中南大学机电工程学院，湖南长沙，410083；2. 韶关学院物理与机电工程学院，广东韶关，512005)

梁结构在航空航天、机械、汽车和建筑等领域广泛使用[1-2]。大部分梁结构在使用过程中不仅承受动载荷作用，而且受服役环境的影响。由于腐蚀、温度波动和疲劳等多种原因，梁结构中容易产生裂纹。在动载荷作用下，这些裂纹会不断扩展并导致断裂。因此，梁结构的疲劳裂纹扩展问题一直备受关注。为了保证梁结构的安全可靠运行，在梁结构设计中，迫切需要考虑疲劳载荷的影响，准确预测裂纹扩展寿命。近年来，国内外一些学者采用经典解析法研究了裂纹梁的振动疲劳问题。例如，LIU等[3]将裂纹等效成扭转刚度，建立了裂纹梁横向振动微分方程，研究了摩擦阻尼对疲劳裂纹扩展寿命的影响；马一江等[4]将裂纹模拟成无质量的弯曲弹簧，建立了含多条裂纹梁的横向振动微分方程，根据边界条件和协调条件推导了应力强度因子表达式，基于Pairs 方程，分析了加载频率对裂纹扩展寿命的影响；刘文光等[5]将裂纹等效成拉伸弹簧和扭转弹簧，建立了裂纹梁的横向振动模型，研究了振动与裂纹扩展耦合关系对疲劳寿命的影响。裂纹梁结构的动力学模型是振动疲劳寿命分析的基础，目前，裂纹梁结构动力学建模方法主要有经典解析法[3-6]和有限单元法[7-9]。例如，REZAEE等[6]基于弹性力学建立了裂纹梁的动力学方程，研究了裂纹位置和尺寸对裂纹梁稳态响应的影响；ANDREAUS 等[7]采用有限单元法建立了裂纹梁的运动方程，研究了裂纹闭合效应对裂纹梁动态响应的影响。在经典解析法中，首先建立裂纹梁弹性力学方程，然后，根据边界条件和裂纹处的协调条件求得解析解。但是，由于梁结构的形状和载荷作用方式多样，除了少数比较简单梁结构外，按经典弹性力学方法获得解析解十分困难，甚至不可能[10]。另外，考虑裂纹扩展影响时，裂纹梁的刚度呈现时变性，裂纹梁动力学方程是非线性的，不可能直接求得其解析解[7]。为了求得近似解析解，即使是简单的含裂纹悬臂梁弹性力学方程，也需要简化成单自由度模型分析[5]，局限于分析第1阶模态的影响[8]。与经典解析法不同，有限单元法能考虑更多的自由度，裂纹梁有限元模型能准确模拟裂纹梁的动态响应[9]，还能应用于复杂梁结构分析[11]。此外，有限单元法采用数值方法不仅能直接计算响应，而且能更好地求解非线性方程[7]。然而，目前，在研究裂纹梁结构振动疲劳时，鲜见采用有限单元法建立裂纹梁结构疲劳寿命预测模型的相关报道。为了建立裂纹梁结构疲劳寿命预测模型，本文作者基于有限单元法建立裂纹梁结构的动力学模型。根据裂纹梁单元的特点，推导裂纹梁单元的应力强度因子表达式，在此基础上应用Walker 方程建立疲劳裂纹扩展增量计算式，基于振动响应与裂纹扩展循环同步分析法，计算疲劳裂纹扩展寿命。

1 裂纹梁单元的刚度矩阵

裂纹梁单元模型如图1所示。裂纹梁单元包含2 个节点，每个节点包括3 个自由度，即轴向位移u，横向位移v和转角θ。相应节点力分量分别为轴向力F、剪力P和弯矩M。裂纹为单边裂纹，在梁的宽度方向扩展一致。为了分析简便又不失普遍性，这里没有考虑裂纹表面接触的影响。基于欧拉伯努利梁假设，忽略剪切变形对裂纹梁的影响，在线弹性范围内，无裂纹梁单元的应变能W0可表示为[12]

式中：E为弹性模量；I为惯性矩；l为梁单元长度；A为梁的横截面积；F1，P1和M1分别为单元左端节点的轴向力、剪力和弯矩。

根据线弹性断裂力学，裂纹产生的额外应变能W1可表示为[13]

图1 裂纹梁单元模型Fig.1 Schematic model of cracked beam element

式中：Ac为裂纹面积；J为应变能释放率。

根据Griffith-Irwin 理论，应变能释放率J可表示为[14]

式中：对于平面应力，E＇=E；对于平面应变，E＇=E/(1-ν2)，υ为泊松比；KI，KII和KIII分别为张开型、滑开型和撕裂型裂纹的应力强度因子。根据图1中裂纹梁单元的受载形式，只考虑张开型(I型)和滑开型(II型)断裂的影响，应变能释放率J进一步表示为

式中：KIF，KIP和KIM分别为纵向力、横向力和弯矩产生的张开型裂纹应力强度因子；KⅡP为横向力产生的滑开型裂纹应力强度因子。

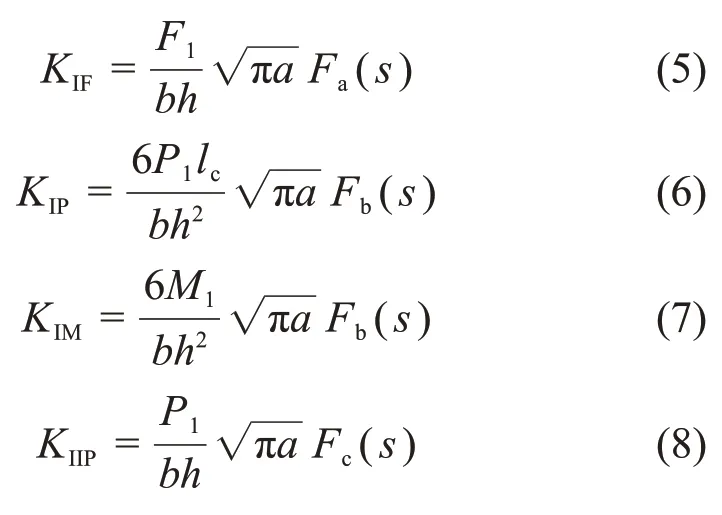
式中：s为裂纹相对深度，s=a/h，a为裂纹深度，h为梁高度；b为裂纹梁宽度；lc为裂纹位置到单元左端节点的长度。应力强度因子的修正函数Fa(s)，Fb(s)和Fc(s)分别为[15]

根据卡氏定理，无裂纹梁单元的柔度系数表示为[15]

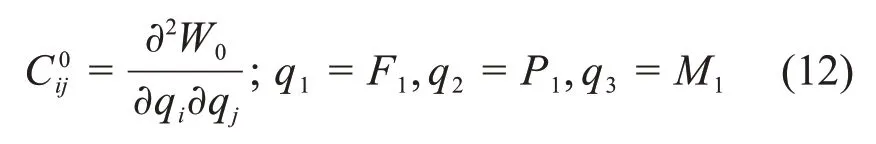
裂纹梁单元的总柔度系数Cij可表示为

根据图1中裂纹梁单元的节点力，裂纹梁平衡条件表示为

根据虚功原理，裂纹梁单元的刚度矩阵kc可表示为

式中：C=C0+C1，C0为由无裂纹梁单元的柔度系数Cij组成的矩阵，C1为由裂纹引起的柔度系数组成的矩阵。由以上推导可知：裂纹梁单元刚度矩阵kc与裂纹引起的柔度矩阵C1有关；当C1=0时，裂纹梁单元刚度矩阵kc等于无裂纹梁单元的刚度矩阵ke，即kc=ke。

2 裂纹梁结构的振动

根据圣维南原理，裂纹仅影响其附近区域的应力场[12]。因此，当裂纹梁单元长度大于一定值时，裂纹仅影响其单元内的刚度，对相邻单元刚度的影响可以忽略不计[7,12]。为了方便分析，忽略裂纹对梁结构质量和阻尼影响，也就是说，裂纹梁单元的质量矩阵mc等于无裂纹梁单元的质量矩阵me，其计算模型见文献[16]。

2.1 裂纹梁结构的运动微分方程

由于工程梁结构形状多样，为便于理解一般裂纹梁结构的建模过程，以图2 所示的含裂纹GARTEUR AG-11 结构[17]为例，推导裂纹梁结构的动力学方程。GARTEUR AG-11 梁结构划分为n个梁单元，第2个单元为裂纹梁单元，其他为无裂纹梁单元，每个梁单元的节点包括3个自由度。对于任意第i个单元，其运动方程为

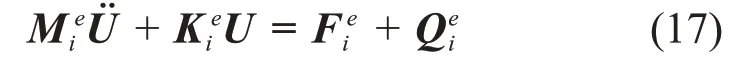
式中：和U分别为整体坐标系下的加速度列阵和坐标列阵；

Bi为第i个梁单元的协调矩阵；Ri为第i个梁单元的坐标转换矩阵；fi为作用于第i个梁单元上的外力；qi为其他梁单元作用于第i梁单元上的单元作用力；mi为第i个梁单元的质量矩阵；ki为第i个梁单元的刚度矩阵，当i=2时，k2=kc，当i≠2时，ki=ke。

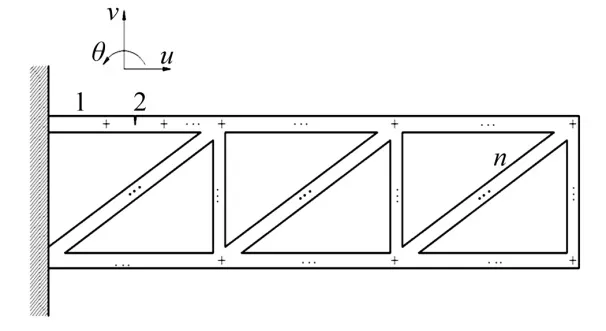
图2 含裂纹GARTEUR AG-11结构的有限元模型Fig.2 Finite element model of GARTEUR AG-11 structure with cracks

将含裂纹GARTEUR AG-11 结构中的n个梁单元的运动方程叠加，采用黏性阻尼模型[16]，得到其运动微分方程：

式中：M为裂纹梁结构的整体质量矩阵，M =K为裂纹梁结构的整体刚度矩阵，K =C为裂纹梁结构的阻尼矩阵；˙为整体坐标系下的速度列阵；F为外力列阵，需要注意的是，各单元叠加后，单元间相互作用力抵消。

由以上推导可知：对其他结构形式的裂纹梁结构也可采用以上方法建立其动力学方程，这说明本文建模方法具有普遍性。

2.2 方程的求解

为求得裂纹梁的瞬态响应，采用Newmark法[16]求解裂纹梁结构动力学方程(22)。选择时间步长Δt、参数r和参数β，取r=0.5，β=0.25，Δt=1/(20f)，其中，f为激振力的频率。

3 裂纹扩展

由于裂纹尖端具有应力奇异性，裂纹梁结构的最薄弱环节一般在裂纹位置。在裂纹梁结构振动过程中，裂纹梁结构的疲劳寿命往往由疲劳裂纹扩展决定。应力强度因子是预测裂纹扩展寿命中的关键参数。与裂纹试件相比，裂纹梁结构形状和载荷作用方式更复杂，目前还没有统一的应力强度因子计算公式。为了准确计算裂纹梁结构的疲劳寿命，本文利用有限元离散性的特点，将裂纹梁单元作为研究对象，通过裂纹梁单元的应力强度因子预测裂纹梁结构的疲劳寿命。

3.1 裂纹梁单元的名义应力

假设梁中性线在裂纹处连续，采用三次埃尔米特插值多项式，图1 中裂纹位置的横向位移v(x)和轴向位移u(x)分别为[16]

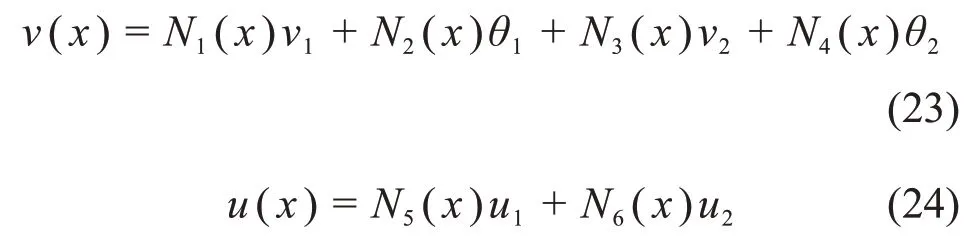
式中：N1(x)，N2(x)，N3(x)，N4(x)，N5(x)和N6(x)为型函数；；。

根据材料力学理论，图1中裂纹位置的弯曲应变和拉伸应变分别为

根据应力应变关系，裂纹位置处的弯曲名义应力σ1和拉伸名义应力σ2分别为

3.2 裂纹梁单元的应力强度因子幅

假定裂纹在扩展过程中沿直线往前扩展。根据裂纹梁单元的应力形式，将弯矩和拉伸引起的应力强度因子叠加，得到裂纹梁单元的应力强度因子KI表达式：

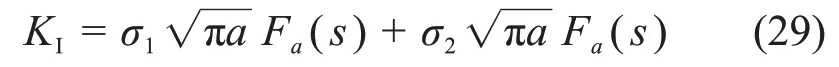
裂纹梁结构在振动过程中，由于名义弯曲应力和名义拉伸应力的变化，应力强度因子也一直处于动态变化中。因此，在1个振动周期内，裂纹梁单元的应力强度因子幅ΔKI表示为

式中：KImax和KImin分别为1 个周期内应力强度因子的最大值和最小值。

3.3 裂纹扩展速率

目前，已有许多关于裂纹扩展速率da/dN与ΔKI关系的经验公式。Walker 公式考虑了应力比R的影响，对裂纹稳定扩展阶段的适用性较好，是最为广泛应用的公式之一[18]。Walker公式的表达式如下：

式中：C0，m和γ为材料常数。

由于应力强度因子幅ΔKI动态变化，式(31)不能直接积分得到裂纹扩展增量，必须采用数值积分计算。为了分析简便，取每1个振动周期作裂纹扩展计算，即ΔNi= 1，则1 个振动周期内裂纹扩展增量为

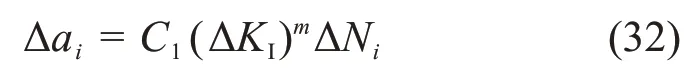
由于裂纹在当前振动周期扩展Δai，裂纹梁结构的刚度K相应改变。为了计算下1个振动周期的裂纹扩展量Δai+1，首先需要重新计算裂纹梁结构的振动响应U，然后求出裂纹梁单元的应力强度因子幅ΔKI，再根据式(32)求得下1 个振动周期的裂纹扩展量Δai+1，通过循环接循环的往复计算，第k次振动周期的裂纹长度ak为

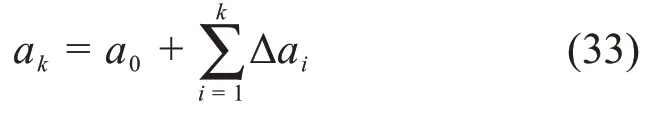
式中：a0为初始裂纹长度。

3.4 裂纹梁结构的失效准则

为了评价裂纹梁结构的疲劳寿命，本文采用失效的准则如下：

1)最大应力强度因子Kmax达到并超过材料断裂韧性KIc，即Kmax≥KIc。

2)非裂纹截面的应力σ大于等于材料的屈服极限σy，即σ≥σy。

3) 当裂纹扩展长度ak到达梁的中性轴时，即ak≥h/2。

4 裂纹梁结构振动与疲劳耦合分析

图3所示为裂纹梁结构的振动与疲劳耦合计算流程图，步骤如下：

1) 输入裂纹梁结构参数，形成质量矩阵M，刚度矩阵K和阻尼矩阵C。

图3 裂纹梁结构振动与疲劳耦合分析流程Fig.3 Flow chart of couple analysis of fatigue and vibration of cracked beam structure

2)输入载荷参数F。

3)计算振动周期T，选择时间步长Δt，参数r和β。

4) 采用Newmark 迭代法计算1 个振动周期内的振幅。

5)计算1个振动周期内的应力强度因子幅ΔKI。

6)计算1个振动周期内的裂纹扩展量Δai。

7)根据失效准则，判断是否达到终止条件。

8)更新裂纹长度，重复步骤4)～7)，直至裂纹梁结构失效为止。

5 仿真分析

简支梁是常用的梁结构之一。为求简便而不失普遍性，采用图4所示的含裂纹简支梁进行数值计算。简支梁的长度为266 mm，宽和高均为20 mm。裂纹位于简支梁中间，初始裂纹长度为1 mm。简支梁的材料为7075-T651 铝合金，其材料参数如表1所示。循环载荷P作用在简支梁的中间，加载的应力比R(R=Pmin/Pmax，Pmax和Pmin分别为载荷最大值和最小值)为0.1。为满足计算精度要求且计算简便，简支梁划分为5个梁单元，每个梁单元长度为53.2 mm，其中，裂纹划分在第3 个梁单元的中间位置。假定阻尼矩阵能使正则振型对其正交，每个模态的正则振型阻尼比为0.05。首先将简支梁的几何参数、材料参数和边界条件代入式(17)～(22)，然后根据频率方程公式[16]，得到含裂纹简支梁的第1阶固有频率f1为684 Hz。

图4 含裂纹简支梁的仿真模型Fig.4 Simulation model of simple supported beam with crack

5.1 载荷频率对裂纹梁疲劳寿命的影响

当最大载荷力Pmax为3 kN，应力比R为0.1时，不同载荷频率下简支梁振动循环次数N与裂纹扩展长度a的曲线如图5(a)所示。由图5(a)可见：在相同最大载荷和应力比下，随着激振频率f从10 Hz增大到539 Hz，裂纹长度从1 mm 扩展到8 mm 的循环次数降低。以f为10 Hz 的循环次数为基准，当f为337 Hz 时振动循环次数降低46%，当f为539 Hz 时振动循环次数降低85%；随着激振频率接近固有频率，含裂纹简支梁的振幅越来越大，裂纹梁单元应力强度因子幅ΔKI增大，疲劳裂纹扩展速率增加，疲劳裂纹扩展寿命降低。

5.2 载荷幅值对裂纹梁疲劳寿命的影响

当应力比R为0.1，加载频率f为10 Hz 时，不同载荷下简支梁振动循环次数N与裂纹扩展长度a的曲线如图5(b)所示。由图5(b)可见：在相同应力比和频率下，随着激振力从3 kN 增大到5 kN，裂纹长度从1 mm 扩展到8 mm 的循环次数降低；随着激振力增大，裂纹位置处的振动幅值增大，裂纹梁单元的应力强度因子幅ΔKI增大，疲劳裂纹扩展速率增加，疲劳裂纹扩展寿命降低。

5.3 应力比对裂纹梁疲劳寿命的影响

当最大载荷力Pmax为3 kN，加载频率f为10 Hz时，不同应力比下简支梁振动循环次数N与裂纹扩展长度a的曲线如图5(c)所示。由图5(c)可见：在相同的最大载荷力和频率下，随应力比R从0 增加到0.5，裂纹长度从1 mm 扩展到8 mm 的循环次数增加。在此需要说明的是，当R＜0 时，一般认为压应力部分对裂纹扩展速率没有影响[18]，也就是说，在相同的最大载荷力下，认为应力比R＜0 和R=0 具有相同的疲劳裂纹扩展寿命。以应力比R为0的循环次数为基准，R为0.1时振动循环次数增加15%，R为0.3时振动循环次数增加62%，R为0.5 时振动循环次数增加155%。随着应力比R增大，应力强度因子的最小值KImin增大，而应力强度因子的最大值KImax保持不变。因此，应力强度因子幅ΔKI降低，疲劳裂纹扩展速率降低，裂纹梁的振动循环次数得到大幅度提升。

表1 7075-T651铝合金的材料参数Table 1 Material data of 7075-T651 aluminum alloy

图5 载荷对裂纹扩展寿命的影响Fig.5 Effect of load on fatigue crack growth

6 试验验证

6.1 7075-T651材料的裂纹扩展试验

试验材料为上海航铝航空材料有限公司提供的7075-T651 铝合金，板厚度为4 mm。材料屈服强度为523 MPa，弹性模量E为71.7 GPa。根据文献[19]，采用标准紧凑拉伸试样开展材料的裂纹扩展试验。试件尺寸如图6(a)所示。在室温条件下，在MTS810 疲劳试验机上进行疲劳裂纹扩展试验。试验施加正弦波恒幅载荷，最大载荷力Pmax为1.2 kN，应力比R为0.1，加载频率f为20 Hz。

6.2 裂纹梁的三点弯曲疲劳试验

为了验证模型的准确性，采用7075-T651铝合金梁进行三点弯曲疲劳试验。梁试件的尺寸如图6(b)所示，长、宽和高分别为400，20 和20 mm。为了预制疲劳裂纹，试件上切割出1个V形槽。搭建的三点弯曲疲劳试验装置包括伺服疲劳试验机(SDS200)、三点弯曲夹具和工业检测视频显微镜(AOSVI AF216C)。为了通过显微镜准确测量疲劳裂纹长度，试样的表面用砂纸抛光处理。裂纹梁通过三点弯曲夹具固定在疲劳试验机上，两端的跨距为266 mm，载荷作用在梁的中间位置。

采用恒幅载荷预制疲劳裂纹，预制出裂纹长度分别为3.153 mm 和3.063 mm 这2 组试件，分别称为试件1 和试件2。试件1 的最大载荷力Pmax为3 kN，应力比R为0.1，加载频率f为10 Hz。试件2的最大载荷力Pmax为4 kN，应力比R为0.1，加载频率f为10 Hz。两者的最大载荷不同，其他载荷一致。

图6 试样尺寸Fig.6 Dimensions of test samples

6.3 试验结果

采用对数坐标处理原始试验数据，紧凑拉伸试件应力强度因子幅ΔK与裂纹扩展速率da/dN的关系如图7 所示。取图7 中ΔK从10 MPa·m1/2到23 MPa·m1/2稳定裂纹扩展区数据，进行采用线性拟合，拟合结果如图8 所示，得到应力比R为0.1时，材料裂纹稳态扩展常数C1为2.205 5×10-7，m为2.116。

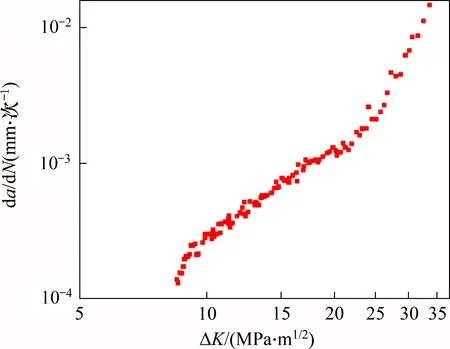
图7 紧凑拉伸试样在R=0.1时da/dN与△K的曲线Fig.7 Relationship between da/dN and △K of compact tension specimen at R=0.1

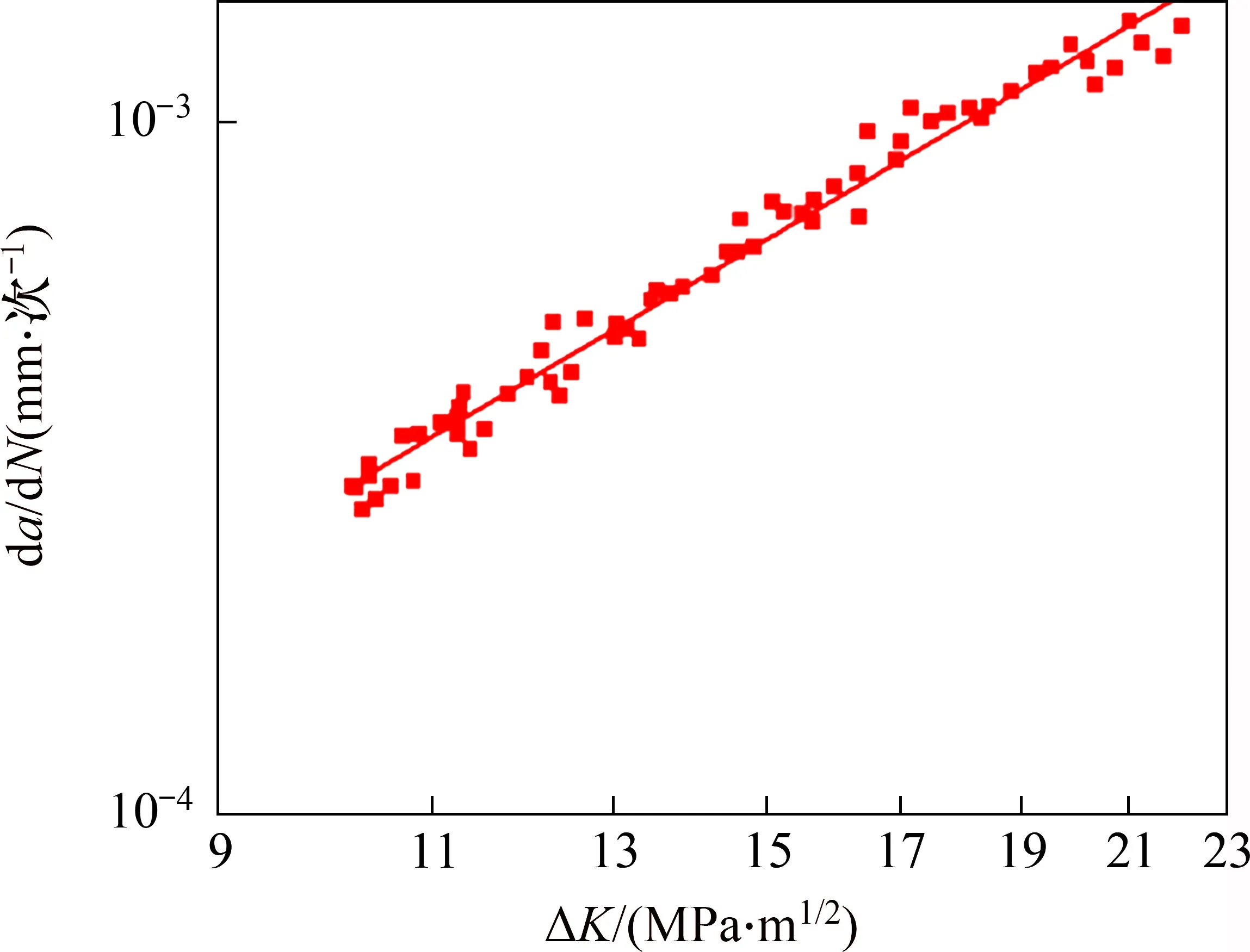
图8 裂纹扩展速率在R=0.1时的拟合结果Fig.8 Fitting results of crack growth rate at stress ratio R=0.1

三点弯曲疲劳试验结果如表2所示。从表2可见：试件1 从裂纹长度3.153 mm 扩展至裂纹长度5.900 mm的循环次数为24 682次。试件2从裂纹长度3.063 mm扩展至裂纹长度5.315 mm的循环次数为12 241次。

6.4 数值分析与试验结果比较

为了验证本文模型的准确性，将本文理论计算的裂纹扩展次数与试验结果对比。由于试验过程中Pmin＞0，裂纹梁在受迫振动过程中始终处于受压状态，在支点处相当于无纵向位移，因此，将图6(b)中的试验结构简化为图4 中的有限元模型，数值计算的疲劳裂纹扩展结果如表2 所示，其中，试件1的振动循环次数为26 600次，试件2的振动循环次数为13 000次。从表2可见：试件1和试件2 的循环次数预测误差分别为7.8%和6.2%。从对比结果看，仿真和试验循环次数的最大误差不超过8.0%，循环次数预测结果与试验结果基本一致，验证了本文提出模型的正确性。