基于变质心高度策略的双足机器人变步长步态规划
2020-06-04周江琛肖晓晖
周江琛,肖晓晖
(武汉大学动力与机械学院,湖北武汉,430072)
双足步行机器人能适应复杂环境,具有高度的灵活性和运动能力,在野外探测、家庭服务等诸多领域有着广阔的应用前景[1]。为提高双足机器人在复杂环境下的运动能力,一方面,机器人应具备通过调整步长来跨越地面障碍的能力,在生成步行模式时要考虑机器人步长调节能力;另一方面,要考虑变步长步行过程中机器人的能量效率。针对变步长步行,众多学者参考ZMP 轨迹生成步态,通过调整ZMP 轨迹以实现目标运动[2-3]。KAJITA等[4]提出一种线性倒立摆模型跟踪控制器,通过调整质心轨迹来减小ZMP误差;冯帅等[5]通过补偿单足相时间,实现机器人质心轨迹平稳过渡并实现变步长步行;张世龙等[6]基于时间补偿和踝关节力矩控制调整ZMP,在步长变化时,在线修正机器人状态,保证稳定步行。与此同时,也有部分研究人员研究人类步行原理,建立更精确的运动模型或者采用仿生学原理,实现双足步行。AFTAB等[7]采用飞轮倒立摆模型(inverted pendulum plus flywheel model, IPFM),通过躯干转动来调整ZMP 以控制落脚点;KUDOH 等[8]通过捕捉人类动作提出迈步策略。另外,一些基于智能控制的方法也得到广泛运用,如刘飞等[9]通过离线学习,建立最优落脚点与躯干姿态模型,实现落脚点调整;ZHONG 等[10]采用神经网络结合模糊逻辑控制器实现复杂地面下机器人运动控制。上述步长调整方法基于恒定高度的LIPM,认为机器人在步行过程中质心高度保持不变,避免由高度变化带来的复杂非线性问题。由于运动学约束,质心高度限制了机器人的步长变化范围,在当步长发生较大改变时,逆运动学无法得出有效解;同时,这类方法忽略了质心高度对机器人的影响。而基于智能控制的方法需要一定的训练时间,对环境适应力较差。研究表明,人类步行过程中躯干高度并不固定且不同环境下具有多样步态,以实现高效稳定步行[11]。同时,在ZMP 稳定裕度内,通过调整步长和线性倒立摆模型高度可以降低机器人能耗[12]。鉴于此,仿人机器人行走的高度调整策略也引起研究者关注。一方面,高度变化带来复杂非线性问题,传统基于参考ZMP 轨迹的步行模式生成器解算困难;另一方面,在实时调整落脚点时,为提高稳定性,必须考虑机器人面临的结构尺寸和稳定裕度等多方面的约束。模型预测控制(model predictive control, MPC)能解决非线性多约束优化问题。目前,已经有学者基于MPC 实现落脚点调整[13]、侧向干扰恢复[14]和机器人上下台阶[15],但这些方法没有关注到变步长步行中质心高度的调整。为此,本文针对仿人机器人变步长步行需求,鉴于传统线性倒立摆步态规划方法中质心高度对步长可变范围的限制,同时考虑倒立摆模型质心高度对步行能量效率的影响,引入高度变化,提出一种基于MPC 的变质心高度的步态生成方法。该方法基于变质心高度策略生成变步长步态,避免了由于运动学约束导致的固定质心高度对步长可调范围的限制;同时,考虑到质心高度对步行能耗的影响,以不同步长下能耗最低的质心高度为参考,通过调整质心高度以提高变步长步行能量效率。
1 双足机器人节能步行
1.1 双足步行步态生成
在LIPM的双足步态生成过程中,将机器人简化为1个三维倒立摆模型,双足步行模式由步行参数生成参考ZMP 轨迹,ZMP 轨迹通过LIPM 生成质心轨迹,再由逆运动学解算各关节角度,生成双足步行步态,其流程如图1所示。
为避免由质心高度变化带来的非线性问题,线性倒立摆模型将质心维持在恒定高度[2]。然而,质心垂直状态会影响机器人的平衡能力和能量效率,例如当质心高度较低时更容易平衡,具有更高的鲁棒性,加速质心向上可以短暂地提高鲁棒性[16],将质心运动维持在恒定高度,导致步态不自然,同时增加了膝关节力矩和速度,降低了能量效率[11]。

图1 基于LIPM生成双足步行步态流程Fig.1 Biped walking gait generation process based on LIPM
1.2 能耗最低质心高度
为验证质心高度对能量效率的影响,同时考虑到机器人变步长步行需求,以Aldebaran Robotics 公司设计的NAOH25 型机器人为实验平台,在稳定性前提下,研究不同步长步行过程中能效最优质心高度。
采用理论计算和实验验证相结合的方法,首先,估算步行能耗,确定能耗最低质心高度;然后,通过样机实验进行修正。
以NAOH25 仿人机器人为平台,重点研究机器人下肢运动。图2 所示为本文采用的杆式模型。由图2可见:将机器人视为由数个连杆组成,每个连杆固定1个局部坐标系,将机器人样机简化成10个自由度连杆模型,Σw表示固定在地面上的全局坐标系,Σb表示机器人腰部中心的局部坐标系,以机器人向前为全局坐标系x轴方向,向左为全局y轴方向,竖直向上为全局z轴方向。
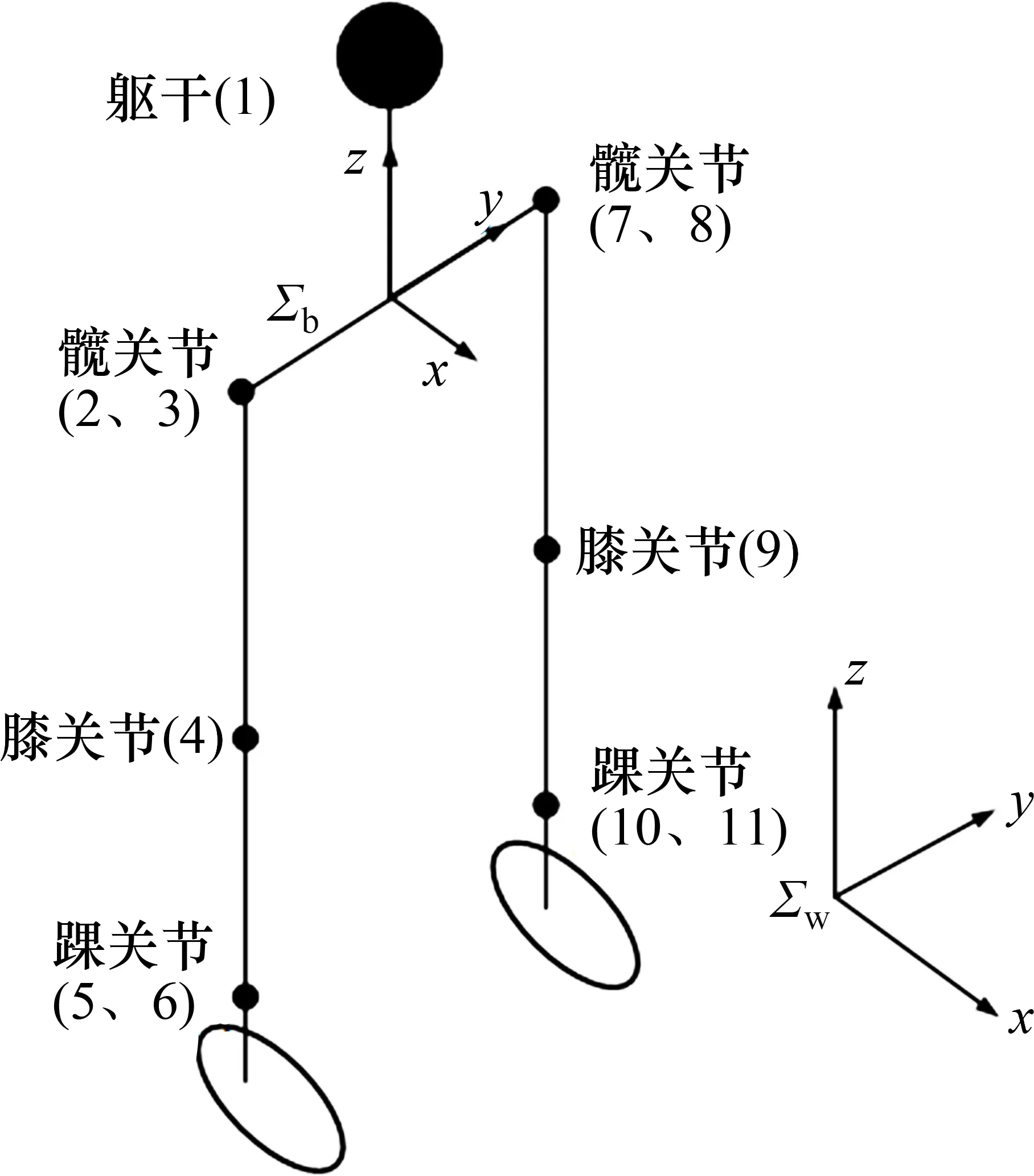
图2 机器人连杆模型Fig.2 Linkage model of robots
由于目前没有能明确描述机器人能量消耗的表达式,所以,通用的评价指标是计算机器人10个关节能耗求和。最重要的是要计算行走所需功率:

式中:Pi为第i段连杆关节功率;τi和分别为第i段连杆关节力矩和角速度。
将单足相ZMP 固定在支撑足中心,由三次多项式规划足部摆动轨迹,生成双足步态[17],得出式(1)中各关节角速度;然后,基于牛顿-欧拉方程,从摆动腿末端向支撑腿依次计算作用在各连杆上的力和力矩,解逆动力学,通过迭代求出各关节力矩,估算能耗[18]。
由牛顿-欧拉定理,图2中第i根连杆的动力学方程为
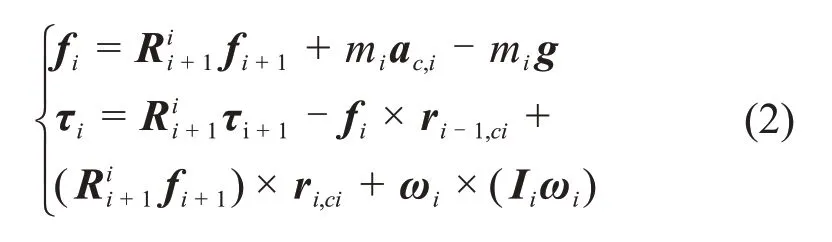
式中:fi和τi分别为连杆和对应关节所受外力和力矩,初值条件fi+1和τi+1为0;ac,i和ωi分别为连杆质心加速度和关节角速度;Ii为连杆惯性张量;为旋转矩阵;ri-1,ci为第i-1坐标系原点到i-1连杆质心位置矢量。
迭代计算各关节力矩,再由式(1)可理论计算双足步行能耗,改变倒立摆模型质心高度,即可得出不同高度下步行理论能耗,获得理论最优高度。考虑模型误差,围绕理论最优高度选取附近区域高度进行样机实验。由于NAO 机器人不具备关节扭矩测量传感器,这里采用电流数据来衡量能量消耗[3],在实验过程中,保持机器人上肢所有关节锁定,即可由下肢运动关节总平均电流即可评估整体能耗。
以步长取0.060 m为例,理论计算能耗最低质心高度为0.318 m,倒立摆高度分别选取0.310,0.314,0.315,0.316,0.318 和0.319 m 进行步行实验,步行周期为1.0 s,单足相时间占80%,每次进行10 个周期的定步长步行,保证每次实验在同样的地面环境下完成。机器人关节平均电流结果如图3所示,由图3可见:定步长步行中不同质心高度下能耗不同,样机实验中,0.060 m 步长下能耗最低质心高度为0.315 m。
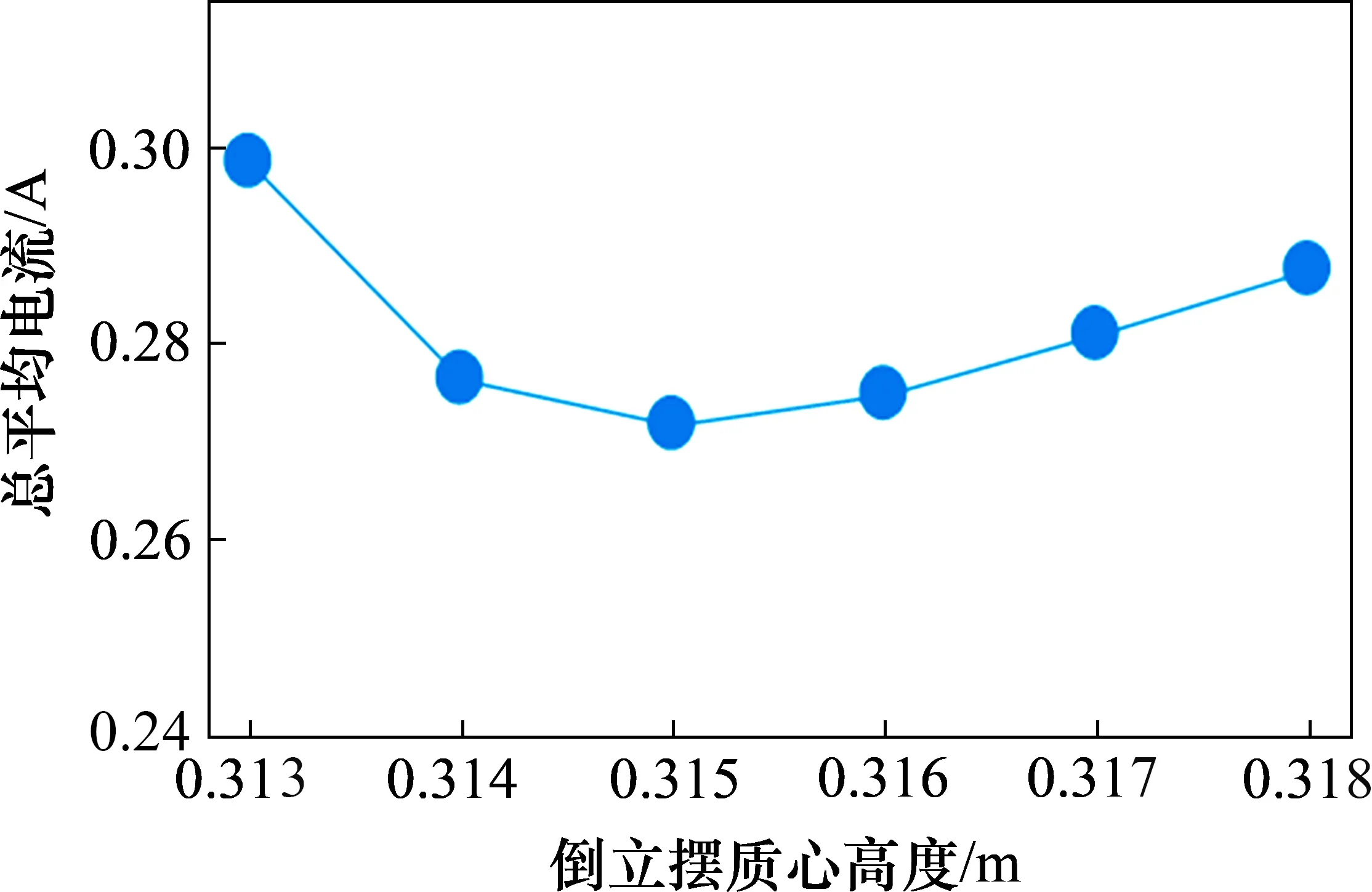
图3 机器人关节平均电流Fig.3 Average current of robot joint
通过样机实验,得出步行周期为1.0 s时6种不同步长下能耗最低时的最优离心高度,结果如表1所示。

表1 不同步长下最优质心高度Table 1 Optimal COM height for variable step-length
2 基于MPC的质心轨迹
2.1 质心状态方程
如上所述,基于固定高度的双足步行在复杂环境中具备较差的变步长步行能力,而机器人在不同步长下具有不同的能耗最低的质心高度。因此,考虑变质心高度情况下的变步长步态生成。将模型预测控制集中在步行机器人的质心运动上,考虑高度变化,质心的状态使用3个变量(xc,yc,zc)来定义,分别表示质心在前向、侧向和垂直方向的位置。
基于MPC 理论,以质心前向、侧向和竖直方向位置的三阶微分为控制输入并假设在每个采样时间间隔Δt内的控制输入保持恒定,以下1个采样时刻质心位置为输出,则在第k个采样时刻,系统状态方程如下:
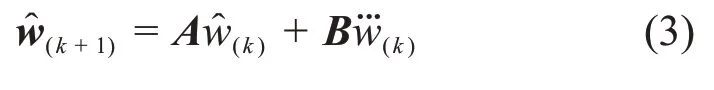
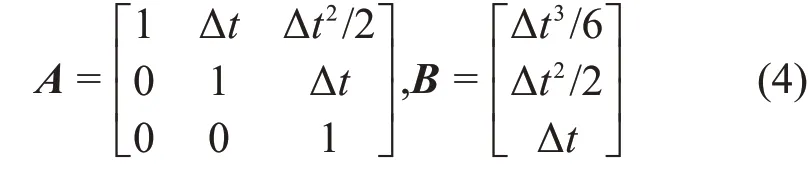
利用上述模型,给定当前状态,在预测域Tpre(包含未来Np个采样时长)内质心位置状态序列W(k+1)=[w(k+1),…,w(k+Np)]T,预测时域内参量速度状态序列和加速度状态序 列可 以 由 下 式表示:

式中:cp=[1 0 0]为位置状态选择矩阵。从质心状态矢量中取出位置分量同理,cv=[0 1 0],ca=[0 0 1]。
2.2 优化目标函数
MPC 的核心问题是通过构建优化目标函数和可行域得到稳定状态下最优输出。给定参考的足部落脚点位置和步行周期(本文中,各周期时长为定值),在优化目标中引入质心水平位置跟踪误差、参考高度跟踪误差和足部落脚点位置误差。此外,考虑机器人驱动能力引入质心速度和输入惩罚。最终,建立如下优化目标函数Fgoal。
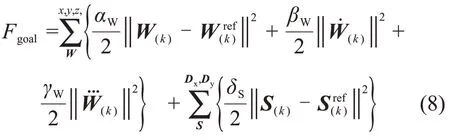
式中:αW,βW,γW和δS分别为位置跟踪惩罚系数、速度惩罚系数、控制输入惩罚系数和足部落脚点跟踪惩罚系数(为保证Hessian矩阵正定性,以上系数均设置为大于0);为预测时域内质心在地面投影位置和高度的参考值;S(k)=[s(k+1),…,s(k+Nf)]T和分别为预测时域所利用的未来Nf个步行周期(除当前支撑周期外)的实际落脚点和参考落脚点位置(s∈{dx,dy});[Dx,Dy]T为预测时域内未来Nf个步行周期前向和侧向足部落脚点位置,如对第k个采样时刻,有Dx(k)=[dx(k,1),…,dx(k,Nf)]T。
式(8)中,输入矢量χ为
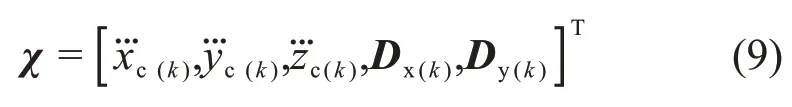
本文提出的目标函数关注于位置跟踪,从而保证机器人能够在变步长步行中跟踪预定足部落脚点。与文献[16]不同,本文考虑到倒立摆模型高度的影响,将质心高度的参考值单独设置,其参考高度与预测周期步长相关联,据表1中不同步长下能耗最低的质心高度,实现质心高度可调的变步长步行。
2.3 约束模型
为保证稳定步行,需要考虑ZMP稳定性约束。高度改变时,以前向运动为例,有
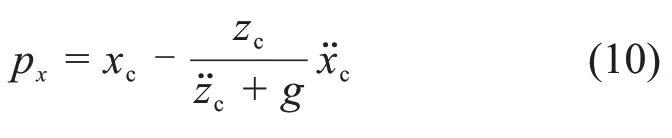
式中:px为ZMP 点的x方向(前向运动)分量;g为重力加速度。根据ZMP 稳定性理论,机器人在行走过程中应该保证ZMP在足部支撑多边形内[2]。由于单足支撑阶段支撑多边形稳定区域最小,并且双足支撑过程ZMP 稳定裕度较大,故本文只考虑单足支撑阶段以简化约束形式。在预测时域内ZMP位置应该满足以下约束:
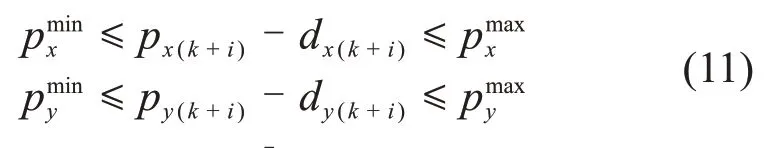
式中:[px(k+i),…,px(k+Np)](i∈[1,Np])为采样时域内所有采样时刻对应的实际ZMP点在全局坐标系下x轴位置,即前向位置;[py(k+i),…,py(k+Np)]为实际ZMP 点在全局坐标系下y轴位置,即侧向位置;[dm(k+i),…,dm(k+Np)](m∈{x,y})为采样时域内所有采样时刻对应的足部中心落点(落脚点);Np为预测时域内采样点数;和分别为x方向上ZMP相对于足部落点的下边界和上边界,由机器人足部尺寸决定;和分别为y方向上ZMP 相对于足部落点的下边界和上边界,由机器人足部尺寸决定。以ZMP 上边界为例,式(11)中ZMP 约束计算如下:
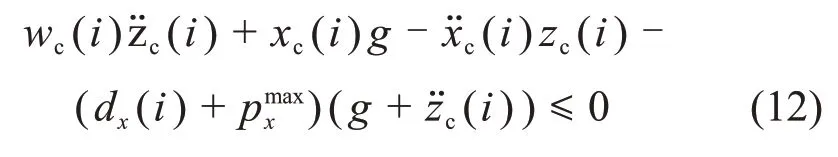
2.4 参考轨迹
在式(8)中,需要给定预测时域内足部参考落脚点、质心地面投影参考位置和质心参考高度。不同周期的足部落脚点可以通过预先指定参考步长和步宽等参数给出。对于实际机器人而言,当前已落下的支撑脚应保持不动。因此,这里需要将当前周期足部落脚点和预先指定的未来周期落脚点映射成整个预测时域的参考落脚点。
在滚动优化过程中,预测时域开始的采样时刻落在当前初始周期,落脚点位置不可移动,而预测时域内未来(Nf- 1)个落脚点位置通过优化函数进行调整。预测时域内参考足部落脚点(以前向落脚点为例)可由下式计算:
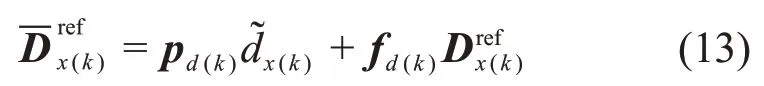
针对参考质心位置,将其在地面的投影位置关联到每个周期的支撑脚中心位置(即各个周期的落脚点)。以前向运动为例,在预测时域内第k个采样点质心参考位置为

本文关注于变步长过程中质心高度的调整,因此,每个周期,式(8)中质心参考高度与当前周期步长关联,以实现高度可调变步长步行。

式中:Href为预测时域内质心参考高度,根据预测周期的步长,通过查表1得出对应步长下能耗最低质心参考高度。
2.5 二次约束二次规划问题
结合式(12)的约束方程,式(8)的优化目标函数,优化问题最终可表示成下列QCQP模型:
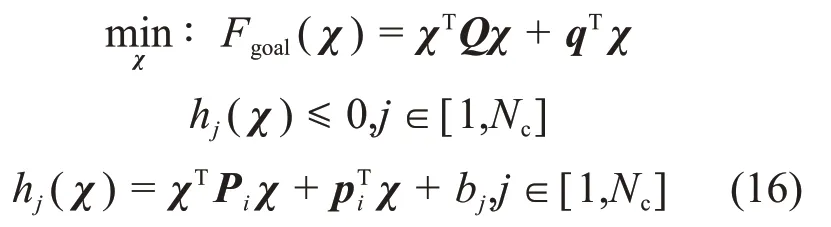
式中:Fgoal(χ)为优化目标函数;hj(χ)为约束函数;χ⊆RNt是由式(9)表示的输入矢量;Q⊆RNt×Nt是目标函数的Hessian 矩阵;Pi⊆RNt×Nt为约束方程的Hessian 矩阵;q∈RNt×1,pi∈RNt×1为1 次项系数矩阵;bj∈R 为约束函数的常数项;Nt和Nc分别为输入变量数目和约束条件数目。
式(16)中目标函数Hessian矩阵Q和1次项系数矩阵q推导如下:
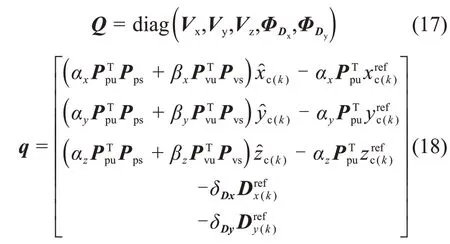
式(17)中diag函数以各矩阵为对角元素生成对角矩阵,各对角元素矩阵计算如下:
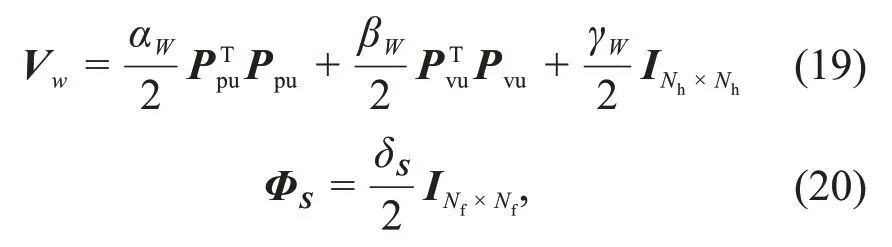
式中:I为单位矩阵。
式(16)中约束方程Hessian矩阵Pi和1次项系数矩阵pi和常数项推导如下:
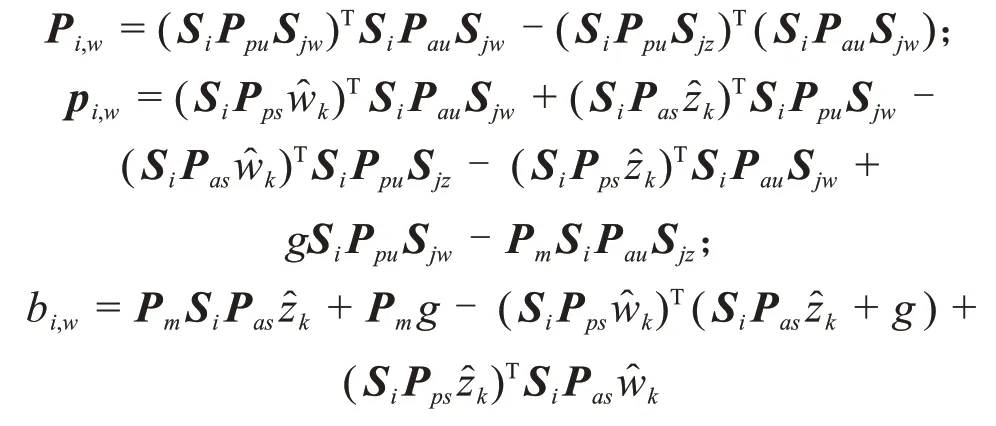
一旦生成式(16)所示的二次约束二次规划问题,则可以转化为序列二次规划(sequential quadratic programming,SQP)求解[19]。采用简单SQP方法,在式(16)中围绕初始迭代点产生以下二次规划问题:
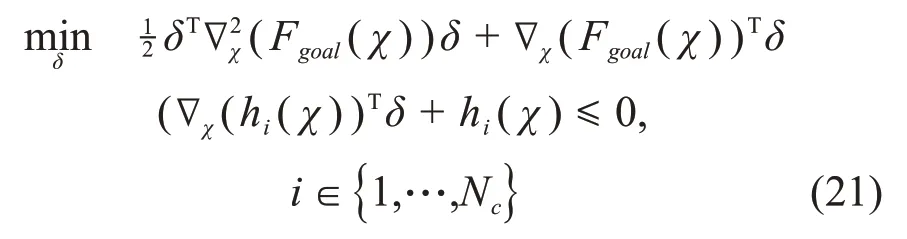
解二次规划,通过χ=χ+δ更新状态变量χ,用新的χ重复解δ,该步骤重复Ns次(本文中取Ns为2,优化问题收敛且计算效率较高)。
为提高优化问题的解算效率,取MPC 模型中预测时域采样间隔大于机器人运动控制采样间隔,即Δt>Δt′,同时保证tpre>1.5tr(其中,tpre为预测时长,tr为步行周期时长),得到的预测时域内的质心轨迹通过三次Hermite插值,得出采样间隔为Δt的轨迹。
3 实验
3.1 实验平台与参数设置
以Aldebaran Robotics 公司设计NAOH25 机器人为实验平台进行实验,其身高为0.574 m,髋关节高度为0.330 m,双足中心间距为0.100 m,质量约5.4 kg,下肢具有12 个自由度,可实现三维步行。
在实验过程中,默认各周期参考步长为0.04 m,参考步宽为0.10 m,摆动腿最大摆动高度为0.02 m。为减小足部与地面的碰撞,摆动腿轨迹采用5次多项式插值。模型参数如表2所示。
3.2 变步长步行
在复杂地面环境下,机器人应具备通过调整步长来跨越地面障碍物和缺陷的能力,本文提出高度可调的变步长调整策略。设计如表3所示的变步长序列参数设置,默认步长为0.040 m,步宽为0.100 m,质心高度为0.320 m。
除表3所列周期步行参数发生改变外,其他周期均使用默认参数。由表3 可见:机器人将从第2个周期开始在前进方向做变步长运动,同时在第12个周期停止。
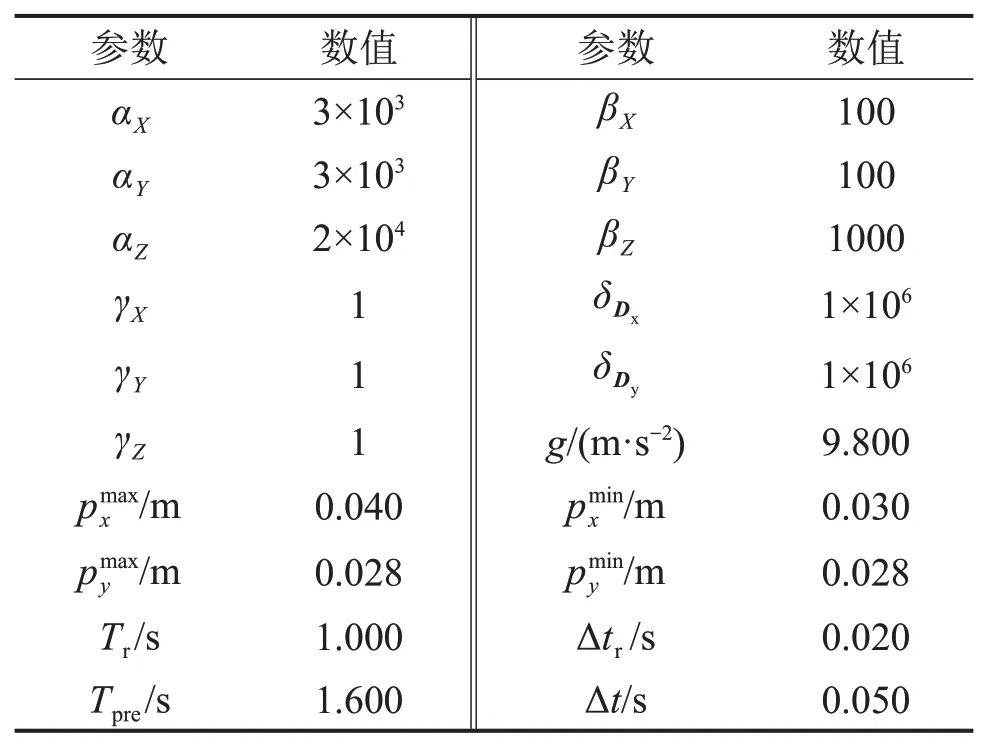
表2 模型参数设置Table 2 Model parameters setup
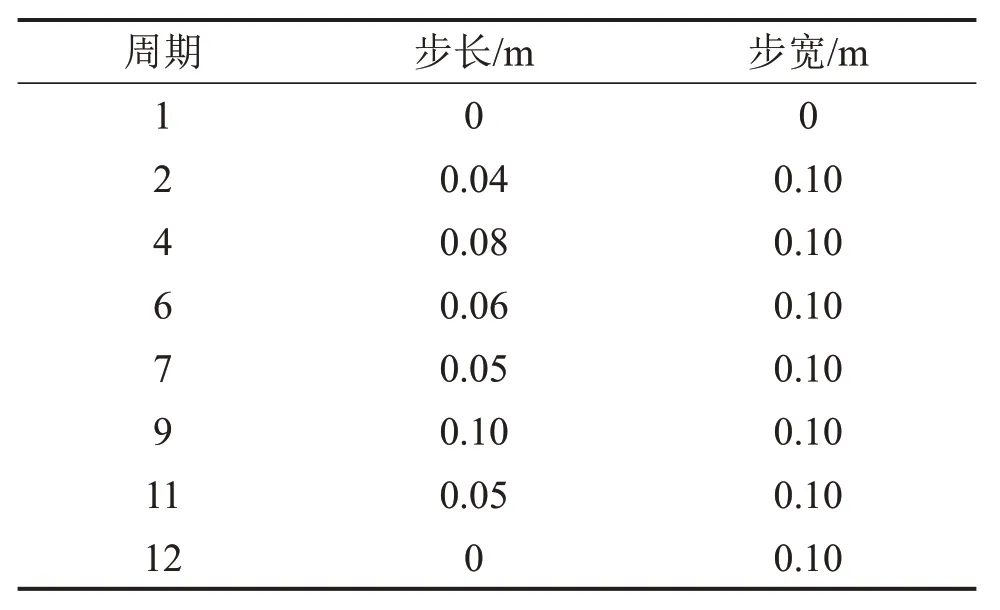
表3 变步长步行参数设置Table 3 Variant step-length parameter setup for biped walking
3.2.1 变步长步行实验
采用本文方法,各周期质心参考高度根据步长选择合适值,具体见表1,生成的质心参考轨迹如图4 所示。由图4 可见:机器人在第4 个周期改变步长,第4周期内质心参考高度也设置为相应能耗最低的高度,而质心在第3 周期内已经开始下降,这显示出MPC 模型的作用,即可根据预测视界内参考状态的变化,提前调整质心轨迹,从而保证约束条件下优化目标函数最优。
分别基于恒定高度LIPM和本文所述方法生成质心轨迹,进行变步长行走对比实验。采用恒定高度LIPM方法生成变步长质心轨迹时,质心高度分别取0.320 m 和0.315 m。这里0.320 m 为默认高度,为步长0.04 m 下能耗最低时的质心高度,而0.315 m 为离线步态生成时,关节角度不出现突变的最高质心高度。实际ZMP 轨迹由机器人足底压力传感计算得出,样机实验结果如图5所示。由图5可见:
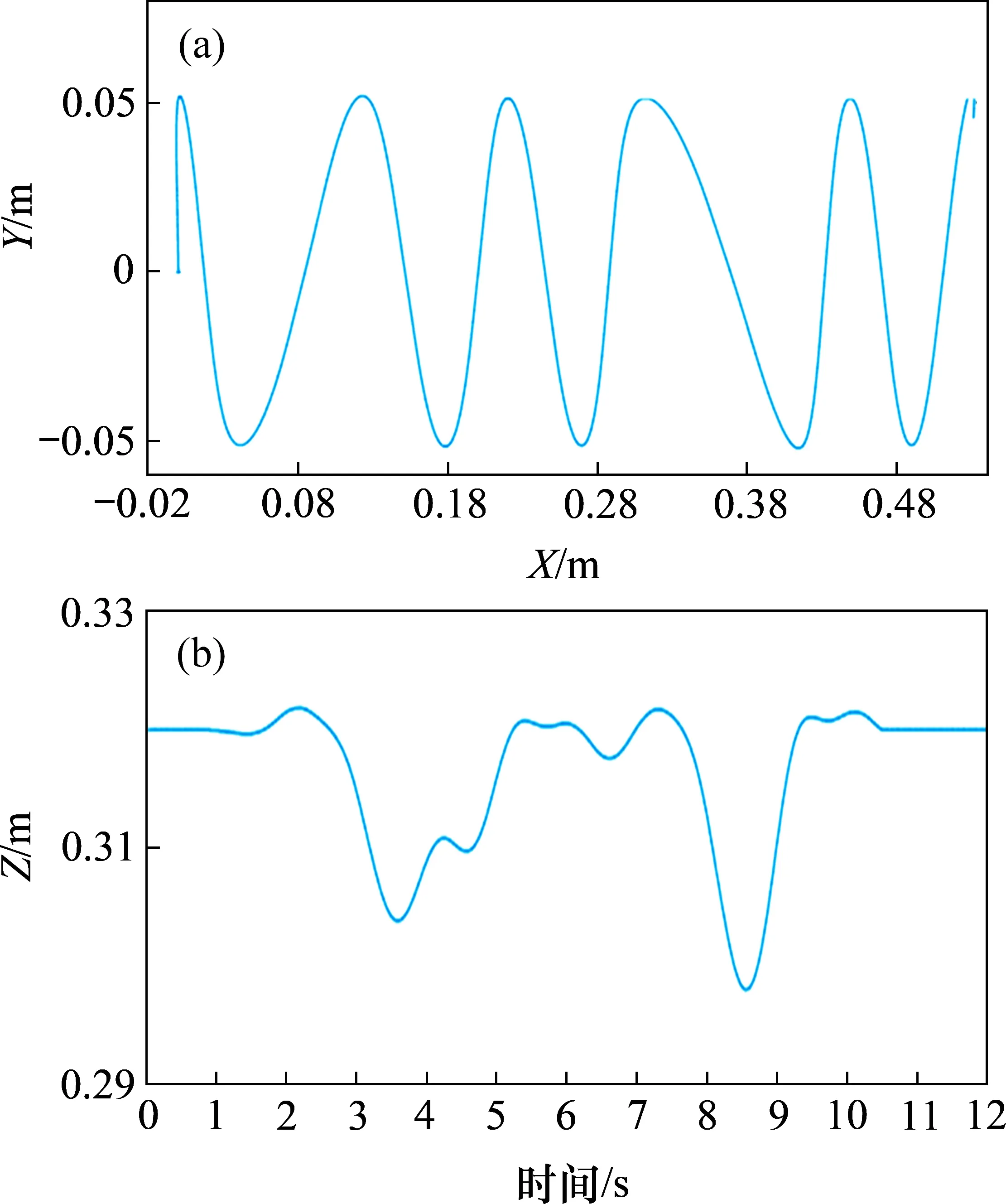
图4 变步长质心参考轨迹Fig.4 COM trajectories for bipedal walking with variant step-length
1) 基于固定高度的LIPM 方法生成变步长步态,在高度取0.320 m 时,机器人在第9 个周期步长增加为0.10 m 时摔倒,无法实现变步长步行,实验中观测到机器人膝关节转动出现突变。
2)基于固定高度的LIPM方法在高度为0.315 m时,能实现变步长行走,机器人实际ZMP 保持在支持区域内。
3)采用本文提出的变质心高度策略的步态规划方法,机器人能通过变质心高度以适应步长变化。机器人在行走过程中能较好地跟踪预定的足部落脚点,机器人实际ZMP 轨迹始终保持在足部支撑区域内,能实现稳定变步长步行。
4)基于变质心高度策略的变步长步态生成方法,可以在较高的初始高度下完成变步长运动,机器人的步长调节范围不受初始高度影响。而在基于恒定高度的LIPM的步态规划方法中,为实现变步长步行,必须选择较低的质心高度。
3.2.2 步行能量效率
NAO 机器人步行实验已经证明,基于变质心高度的变步长步行策略可实现稳定的变步长步行;而对于采用恒定高度的LIPM,为实现变步长运动,由于运动学约束和稳定性约束,必须选择较低的质心高度。
本文通过对比步行实验中机器人能量消耗,衡量传统定高度LIPM方法和本文提出的方法在变步长下的能量。由于在0.320 m的固定高度下机器人未能完成本文设置的变步长行走,这里只对比了固定高度为0.315 m和本文提出的变质心高度方法2组实验结果。实验结果显示,固定质心高度时总平均电流为0.336 8 A,变质心高度时总平均电流为0.279 7 A,机器人关节平均电流如图6所示。
由图6可见:在设定的变步长步行实验中,采用变质心高度策略,机器人单步能耗低于恒定高度的变步长步行能耗,相对于恒定高度,总平均能耗降低约16%。
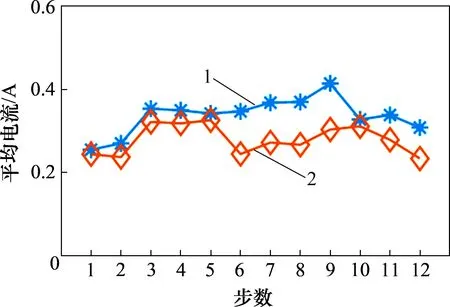
图6 机器人关节平均电流Fig.6 Average current of robot joint
4 结论
1)提出一种基于模型预测控制的高度可调变步长步态生成方法,通过稳定性约束,建立二次约束二次规划求解模型,可生成变高度质心轨迹。
2)基于变质心高度策略的变步长步行相对于恒定高度的变步长步行,平均能耗降低约16%。
3)本文中样机实验基于离线步态,无法应对外力干扰,而MPC 可支持在线轨迹生成和优化,这有待进一步研究。在下一阶段的研究中,将在线生存质心轨迹,同时考虑上身运动,以生成更加仿人的步态,提高变参数步行过程中机器人的稳定性和鲁棒性。
