f- SOBI 算法在fMRI 脑区定位中的应用

2020-06-04陈安莹

科学技术创新 2020年13期

陈安莹

（云南民族大学电气信息工程学院，云南昆明650500）

二十世纪九十年代初，人们发现了功能磁共振成像（fMRI,functional Magnetic Resonance Imaging）技术,该技术通过血氧水平依赖（BOLD, Blood oxygenation level-dependent ）对比技术来探测大脑活动区域。随着fMRI 技术的发展，越来越多的处理方法[2]也应运而生，从最初的检验[1]方法到现在常用的独立分量分析方法。然而这些方法要么需要提前知道数据相关信息要么算法的复杂性太高，为了减少这些缺陷带来的影响，我们考虑用f-SOBI 算法[3]来处理fMRI。

1 fMRI 数据获取的实验方案

本实验的fMRI 数据是在MATLAB 环境下，通过工具箱SimTB（simulation toolbox）模拟的一个听觉怪异任务（Auditory Oddball Task,AOD）, 它指的是在一系列规则且不同的声音中检测到不常见的声音。在本实验的模拟中，我们假设有五名受试者参与实验，每个受试者最多包含27 个脑区，每个脑区的体素为V= 148× 148,任务的重复时间（TR）为两秒，时间扫描数设置为150。

2 fMRI 处理的数据模型

在Simtb 中，人们采用与独立成分分析（ICA）的时空可分离性假设相一致的数据生成模型，那么fMRI 数据模型可表示为

3 实验的结果与对比分析

3.1 数据的处理

在MATLAB 平台下，通过GIFT 软件包对fMRI 数据进行空间独立分析[4]。首先将f-SOBI 算法写入到软件中相应的算法代码中。然后，通过该软件对fMRI 数据进行分析。其中，f-SOBI 算法和fastICA 算法的参数设置如下：

3.1.1 f-SOBI 算法

X：一个二维的数据矩阵，每行代表一个时间点，每列代表一个脑区体素。p:表示对角化的相关矩阵数，在实验中设置为4。

3.1.2 FastICA 算法

完成参数设置后，我们就可以得到一个关于数据的参数文件，然后通过GIFT 软件对该参数文件进行分析就可以提取出相应的脑区图。

3.2 分离性能的对比分析

为了对这两种盲分离算法的分离效果作比较，我们引用常用的盲信号分离性能的评价指标[5]：基于分离矩阵W 和混合矩阵A 的评价准则,表达式为

表1 两种算法的PI 比较

从表1 中可以看出，f-SOBI 的PI 值与fastICA 的PI值差不多，这说明f-SOBI 算法的分离效果与fastICA 的分离效果差不多。

3.3 计算复杂度和运行时间的比较

图1 算法的脑激活区仿真图

的乘法次数，那么这两种算法的计算复杂度及运行时间如表2所示。

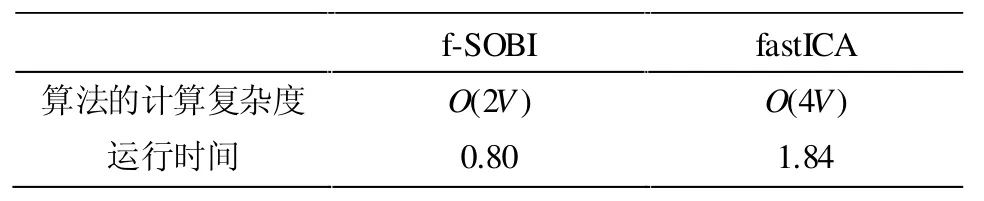
表2 两种算法的计算复杂度及运行时间

从表2 中乘法次数及运行时间都可以看出，fastICA 算法的复杂性要高于f-SOBI 算法，这表明f-SOBI 算法提高处理fMRI数据的效率。

3.4 提取的脑成分图对比

利用在MATLAB 环境下的GroupICA 工具箱对这两种用于fMRI 数据分离的盲分离算法进行仿真，得到的脑区如图1。

从图1 中可以看出，f-SOBI 算法和fastICA 算法都可以从fMRI 数据中提取27 个脑区。这说明该算法可用于fMRI 数据的分离。f-SOBI 算法分离出的脑激活区范围要略小于fastICA 算法分离出的脑激活区范围，而分离出的脑激活区位置基本一致。这说明两种算法用于fMRI 数据脑区定位的效果相差不大。