平面复合金属微纳结构的圆二色性研究*
2020-06-04吐达洪阿巴屈瑜白俊冉张中月
吐达洪·阿巴 屈瑜 白俊冉 张中月
(陕西师范大学物理学与信息技术学院, 西安 710119)(2020年1月18日收到; 2020年3月17日收到修改稿)
圆二色性效应在圆偏振器、光调制器及光电器件等方面具有广泛的应用. 为提高平面金属微纳结构的圆二色性, 本文设计了由无限长纳米线和G 形微纳结构组成的平面复合金属微纳结构, 并应用有限元方法研究了该阵列微纳结构的圆二色性特性. 数值计算结果显示, 在圆偏振光的激发下, G 形微纳结构和平面复合金属微纳结构均出现了电偶极子、电四极子和电八极子等共振模式. 当G 形微纳结构与无限长纳米线连接时,各共振波长均发生红移, 并且无限长纳米线增加了不同圆偏振光激发下的局域表面等离激元共振强度, 从而使得平面复合微纳结构的圆二色性信号明显增强. 此外, 还研究了平面复合微纳结构阵列的几何参数对其圆二色性特性的影响. 这些结果为提高平面手性微纳结构的圆二色性信号强度提供一定的指导思路和方法.
1 引 言
手性是指结构不能与其镜像重合的性质. 手性结构与其镜像称为手性对映体. 然而, 天然的手性结构由于光与物质的电磁作用较弱[1,2], 手性效应相对较小, 因此阻碍了其更广泛的应用. 而周期性排列的手性金属微纳结构与光之间存在强烈耦合作用, 这大大提高了光-物质作用的强度[3], 使得手性效应得到增强. 光与手性金属微纳结构的强作用将被增强的电场限制在纳米尺寸范围内, 进而这些微纳结构表现出独特的光学手性, 例如圆二色性(circular dichroism, CD)[4,5]、光学旋光性(optical rotation, OR)[6,7]和负折射率[8,9]. 其中, CD 效应是指手性结构对左旋圆偏振(left-hand circular polarization, LCP)光和右旋圆偏振(right-hand circular polarization, RCP)光的吸收差异[5]. 它在分析化学[10,11]、生物监测[12,13]和纳米成像技术[14,15]等领域具有重要的应用.
近年来, 研究者们设计了多种手性金属微纳结构, 并探索了CD 效应产生的物理机理. 其中, 三维的手性微纳结构由于多层之间的强烈近场电磁场耦合作用, 可实现比平面人工微纳结构更大的CD 效应, 例如三维L 形[16]、扭曲[17]、螺旋[18,19]和U 形谐振器[20,21]等微纳结构. 相比于三维微纳结构, 平面微纳结构对实际制造工艺的要求较低, 更有利于其广泛应用. 所以, 最近, 平面手性微纳结构引起了研究者的注意. 研究者们设计了各种平面的微纳结构, 并在理论[22,23]和实验[24]上证实了强烈的光-物质电磁作用. 在平面手性人工微纳结构中, 如万字符[25]、七聚体[26]和交叉切口[27]等,CD 效应可归因于强烈的局部表面等离激元(local surface plasmon, LSP)或者表面等离极化激元(surface polasmon polariton, SPP)共振模式. 此外, 在平面非手性微纳结构中, CD 效应可以通过斜入射来实现[28,29]. 金属微纳结构的共振模式对微纳结构的形状、几何尺寸、材料以及周围环境很敏感, 这为调节平面金属微纳结构的CD特性提供了一个可行的技术途径.
本文设计了平面复合金属微纳结构(planar composite metal nanostructure, PCMN)阵 列.PCMN 是由无限长纳米线和G 形纳米结构组成的. 本研究中, 采用数值计算来研究了PCMN 阵列的CD特性. 作为对比, 本文也研究了G形微纳结构 (G-shaped nanostructure, GNS)阵列的CD特性. 通过分析共振波长处的表面电荷密度分布, 揭示了CD 效应产生的物理机理和CD 信号增强的内在原理. 此外, 还研究了PCMN 的几何参数对CD特性的影响.
2 计算方法和结构
本文应用三维有限元方法软件(COMSOL Multiphysics)中的射频模块计算微纳结构的光学特性, 分析了PCMN 阵列的吸收光谱、CD 光谱和其共振波长处的表面电荷密度分布. 图1(a)是所设计的PCMN 阵列的结构示意图. 在本研究中,x和y方向的周期分别定为Px=Py= 0.26 µm.PCMN 阵列的厚度为t. 右旋和左旋圆偏振光分别表示为RCP 和LCP. 图1(b)显示在xy平面上的单元结构示意图. 其中, 无限长纳米线和G 形纳米结构的宽度分别为w1和w2, G 形纳米结构沿着x或者y方向的各纳米棒的长度分别为l1,l2,l3,l4以及l5. 二氧化硅(SiO2)作为基底, 其厚度固定为0.02 µm. 金属的折射率取自于实验结果[30],SiO2的折射率为1.45. 激发源是沿–z方向的RCP 和LCP 光, 入射光波的电场的大小设定为1 V/m.
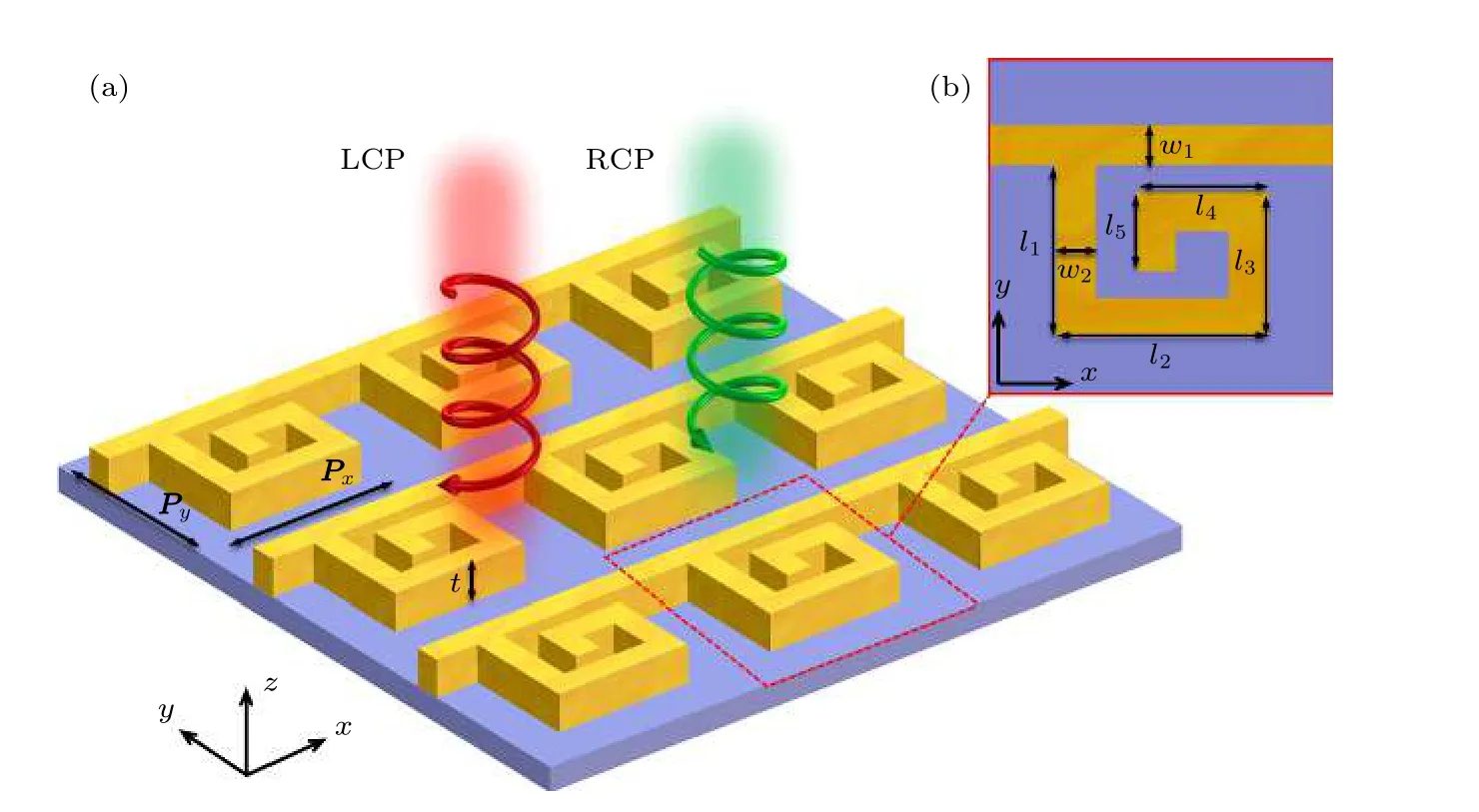
图1 PCMN 阵列的结构示意图 (a)三维立体结构示意图; (b)在xy 平面的单元结构示意图Fig. 1. Schematic of the proposed PCMN arrays: (a) Three dimensional schematic of PCMN; (b) unit schematic of PCMN in xy plane.
在计算中, 在微纳结构的上面和下面分别设置光的入射端口和接收端口, RCP光的三个电场分量分别为光的三个电场分量分别为Ez=0. 使用具有沿x和y方向的周期性边界条件单元来模拟PCMN 阵列的光学特性. 通常, 在手性金属微纳结构与光的相互作用中, CD 特性起源于微纳结构中的电偶极矩(P)或者磁偶极矩(M)的共振, 可以表示为[31]
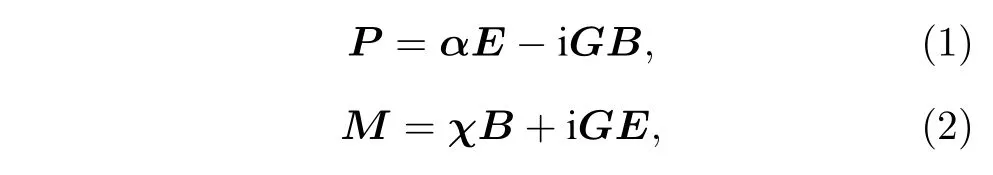
其中a 是极化率,c是磁化率,G是混合电磁偶极子极化率,E和B分别是光波的电场和磁场强度.因此, 手性金属微纳结构中发生共振而吸收(A)光的强度表示为[31]

其中w是入射光的角频率. 在本文中, PCMN 阵列的RCP 和LCP 光的吸收光谱分别表示为A+和A−, 该结构的吸收率是通过在不同偏振光照射下对结构的总功率进行体积分来获得, 则CD 被表示为 C D=A+−A−.
3 结果与讨论
图2 显示了RCP 和LCP 光入射情况下,PCMN 阵列和GNS 阵列的吸收光谱和CD 光谱.其光谱波段范围为从0.30 至6 µm. PCMN 阵列的几何参数为t= 0.03 µm,w1=w2= 0.03 µm,l1 = 0.15 µm,l2= 0.16 µm,l3 = 0.11 µm,l4 =0.10 µm 以 及l5 = 0.06 µm. 图2(a)所 示 的 是PCMN 阵列的A+光谱和A–光谱, 本文用模式I,II, III 和IV 来分别表示各共振模式.A–光谱中分别在lI= 3.14 µm,lII= 1.46 µm,lIII= 0.90 µm和lIV= 0.82 µm 处出现了四个显著的吸收峰.A+光谱与A–光谱类似,A+光谱中分别在lI=2.3 µm,lII= 1.1 µm,lIII= 0.78 µm 以及lIV=0.7 µm 处出现四个吸收峰. 如图2(b)所示, 在共振模式处的吸收差异导致了较强的CD 信号. 图2(c)为GNS 阵列的吸收光谱, 为了与PCMN 阵列的共振模式区分开, GNS 阵列的共振模式用1, 2,3 和4 来表示. GNS 阵列的A–光谱中分别在l1=2.30 µm,l2= 1.10 µm,l3= 0.78 µm 和l4=0.70 µm 处出现了明显的吸收峰. GNS 阵列的A+光谱与A–光谱的共振波长几乎相同. 图2(d)为GNS 阵列的CD 光谱. GNS 阵列的圆二色性信号强度明显地小于PCMN 阵列的圆二色性信号强度.

图2 PCMN 和GNS 阵列的吸收光谱以及CD 光谱 (a), (c) PCMN 和GNS 阵列的A+, A–光谱; (b), (d)PCMN 阵列和GNS 阵列的CD 光谱; 其中插图分别表示PCMN 和GNS 在xy 平面的结构示意图Fig. 2. Absorption and CD spectra of PCMN and GNS arrays: (a), (c) Simulated A–, A+ spectra; (b), (d) CD spectra of PCMN and GNS arrays. The insert figures indicate the structure schematic of PCMN and GNS in x-y plane, respectively.
为了揭示PCMN 和GNS 阵列CD 效应的物理机理, 本文计算了其共振波长处的表面电荷密度分布(如图3 所示). 图中, “+”表示正电荷(深红色), “–”表示负电荷(深蓝色). 图3(a)—图3(h)分别为PCMN 阵列在不同共振波长处的表面电荷密度分布, 图3(i)—图3(p)分别为GNS 阵列在不同共振波长处的表面电荷密度分布. 对于PCMN 阵列, 在LCP 光照射下, 在lI= 3.14 µm 处, 如图3(a)所示, 正电荷主要分布在G 形结构的一端, 负电荷主要分布在无限长纳米线处, 此集聚的表面电荷产生了从G 形微纳结构的一端到无限长纳米线的环形电子振荡. 根据电荷分布的特点, 把它可以视为G 形微纳结构与无限长纳米线之间的电偶极子共振. 在lII= 1.46 µm 处, 如图3(b)所示, 在PCMN结构上形成了扭曲的电四极子共振. 类似地, 在lIII= 0.90 µm 和lIV= 0.82 µm 处, 如图3(c)和图3(d)所示, PCMN 单元结构上形成了电八极子共振. 如图3(g)和图3(h)所示, G 形纳米结构的末端和水平纳米棒的耦合将电八极子模式分裂为两个模式. 对于GNS 阵列, 如图3(i)—图3(l)所示,l1= 2.3 µm 和l2= 1.10 µm 分别为电偶极子共振和电四极子共振模式;l3= 0.78 µm 和l4=0.70 µm 为电八极子共振模式.
PCMN 与GNS 相比, 加了无限长纳米线后,在PCMN 中的电子的振荡距离变长, 使得此四个模式的共振都发生红移. 这些等效的电偶极子、电四极子和电八极子的强烈振荡引起了不同共振波长处的吸收峰, 不同圆偏振光激发下共振强度上的差异, 从而产生CD 信号.

图3 不同偏振的入射光照射在PCMN 和GNS时, 在共振波长处的表面电荷密度分布; 图(a), (b), (c), (d), (i), (j), (k)和(l)是为左旋偏振光; 图(e), (f), (g), (h), (m), (n), (o)和(p)是为右旋偏振光Fig. 3. Surface charge density distribution of proposed PCMN and GNS at the resonant wavelength with different circularly polarized illuminations: (a), (b), (c), (d), (i), (j), (k) and (l) for LCP light; (e), (f), (g), (h), (m), (n), (o) and (p) for RCP light.
为了研究PCMN 阵列的几何参数对共振模式的影响, 如图4 所示, 在各参数w1= 0.03 µm,l1 = 0.15 µm,l2 = 0.16 µm,l3 = 0.11 µm,l4 =0.10 µm 以及l5 = 0.06 µm 的基础上, 本文分别改变了竖直和横向纳米棒的长度l1,l2,l3,l4,l5 和无限米线和长度为l4 的纳米棒之间的库仑力的相互吸引作用逐渐减弱, 这将导致电偶极子共振距离减少, 进而使模式I 的共振波长微小地蓝移. 对模式II 而言, 无限长纳米线和长度为l4 的横着的纳米棒之间的相互排斥的库仑力作用逐渐减弱, 这将导致电偶极子共振距离增大, 从而使模式II 的共振波长发生红移. 如图4(b)所示, 当长度为l2 的横着的纳米棒逐渐从110 nm 增大到150 nm时候,长度为l2 的纳米棒上电荷振荡距离微小增大(如图3(a)所示), 进而使模式I 的共振波长发生很小的红移. 对于模式II 而言, 整个长度为l2 的纳米棒上电荷符号相同, 因此, 当长度为l2 的纳米棒增大时, 模式II 的共振波长没有发生移动. 如图4(c)所示, 随着长度为l3 的纳米棒逐渐从98 nm 增加到120 nm, 无限长纳米线和长度为l4 纳米棒之间的相互吸引的库仑力作用增强, 使得电偶极子共振距离增加, 进而使模式I 的共振波长发生明显地红移. 与此相反, 在模式II 处, 无限长纳米线和长度为l4 的纳米棒之间的相互排斥的库仑力作用增加,使得PCMN 中的电荷振荡距离减少, 并进而使模式II 的共振波长发生蓝移. 如图4(d)所示, 当长度为l4 的纳米棒从50 nm 逐渐增大到90 nm时,长度为l1 的纳米棒和长度为l5的纳米棒之间的相互吸引的库仑力增大, 使得PCMN 中的电荷振荡距离增加, 进而使模式I 和II 的共振波长都发生显著的红移. 当长度为l5 的纳米棒从18 nm 逐渐增到42 nm时, 如图4(e)所示, 长度为l2 的纳米棒和长度为l5 的纳米棒的末端处的相互吸引的库仑力作用增加(如图3(a)和图3(b)所示), 使得PCMN中的电荷振荡距离增加. 显然, 模式I 与II 相比,在模式II 中的相互吸引的库仑力作用比模式I 强,因此, 模式II 的共振波长与模式I 的共振波长相比发生显著的红移. 如图4(f)所示, 随着宽度为w1的无限长纳米线从10 nm 增加到50 nm时, 对模式I 而言, 在无限长纳米线横截面上的集聚电荷增多, 使无限长纳米线和长度为l4 的纳米棒之间的相互吸引的库仑力作用增强, 进而导致模式I 的共振波长稍微红移. 对模式II 而言, 当宽度为w1的纳米棒增大时, 在无限纳米线上增多的振荡电荷, 使无限长纳米线和长度为l4 的纳米棒之间的相互排斥的库仑力作用增大, 这将导致模式II 的共振波长发生蓝移.

图4 PCMN 阵列不同参数的CD 光谱. 不同长度的(a) l1, (b) l2, (c) l3, (d) l4, (e) l5 纳米棒和(f)不同无限长纳米线宽度w1 的PCMN 阵列的CD 光谱Fig. 4. CD spectra of PCMN arrays with different parameter; CD spectraof PCMN arrays with (a) different l1 (b) different l2, (c)different l3, (d) different l4, (e) different l5 nanorod and (f) different w1 of the infinite long nanowire.
为了研究PCMN 的形状变化对其共振波长的影响, 计算了断开的PCMN 阵列的吸收和CD 光谱, 如图5 所示. 在断开的PCMN 阵列中, 无限长纳米线和G 形纳米结构之间的间距由s表示, 其长度为20 nm, 如图5(a)中右下角的插图所示. 其他结构参数分别为w1= 0.03 µm,l1 = 0.13 µm,l2 = 0.16 µm,l3 = 0.11 µm,l4 = 0.10 µm 以及l5 = 0.06 µm. 如图5(a)所示, 在圆偏振光的激发下, 在吸收光谱中分别观察到了三个明显的吸收峰, 插入的彩色图表示结构图(黄色)和LCP 或RCP 光激发下在断开的PCMN 中吸收峰处的电荷分布(红蓝), 三个不同的符号分别表示各吸收峰处的波长. 在λI′=2.30 µm 处, 主要的正负电荷分别聚集在G 形纳米结构的两端, 产生强烈的环形电偶极子共振, 而在无限长纳米线中左右的电子振荡产生电偶极子共振. 进而在整体上G 形纳米结构和无限长纳米线之间的相互吸引的库仑作用力耦合形成绑定(bonding)模式. 在共振波长λII′=1.10 µm 处, 在无限长纳米线中产生强烈的电子振荡, 并形成电偶极子共振, 而在G 形纳米结构上的电子振荡形成电八极子共振. 进而在整体上G 形纳米结构和无限长纳米线之间的相互排斥的库仑作用力耦合形成反绑定(anti-bonding)模式. 在λIII′= = 0.70 µm 处, 分布在无限纳米线两侧的正负电荷, 形成上下振动的电偶极子共振而在G 形纳米结构中的电子振荡产生电四极子共振. 进而在整体上G 形纳米结构和无限长纳米线之间的相互吸引的库仑作用力耦合形成bonding 模式. 在不同圆偏振光激发下吸收强度上的差异, 进而导致CD 效应, 如图5(b)所示. 这表明通过改变结构参数和形状, 可调节电子的振荡路径和耦合方式, 进而有效地调节CD 信号的位置和强度.

图5 断开的PCMN 阵列的吸收光谱和CD 光谱 (a)吸收光谱; (b) CD 光谱. 插图表示分别在共振波长处的电荷分布(深红-蓝色)和断开的PCMN 在xy 平面上的结构示意图(黄色)Fig. 5. Absorption and CD spectra of the separated PCMN arrays: (a) Absorption spectrum; (b) CD spectrum; The insert figures indicate the charge distribution at resonance wavelength (crimson and blue), and structure schematic(yellow) of separated PCMN in xy plane.
4 结 论
本文提出了由无限长纳米线和G 形微纳结构组成的平面复合金属微纳结构, 并应用有限元方法研究了平面复合金属微纳结构阵列的圆二色性特性. 通过分析平面复合金属微纳结构的共振波长处的电荷共振特征, 揭示了CD 特性产生的物理机理和CD 信号增强的内在原理. 数值计算结果表明,在圆偏振光的激发下, G 形微纳结构和平面复合金属微纳结构阵列均出现了电偶极子、电四极子和电八极子等共振模式. 当G 形微纳结构阵列与无限长纳米线互相连接时, 各共振波长均发生了红移,并且无限长纳米线增加了不同圆偏振光激发下的局域表面等离激元共振强度, 从而使得平面复合微纳结构的圆二色性信号明显增强. 此外, 研究了平面复合金属微纳结构阵列的几何参数对CD 的模式的影响. 此研究结果为提高平面手性微纳结构的圆二色性信号强度提供了一定的理论依据.
