ON THE AREAS OF THE MINIMAL TRIANGLES IN VEECH SURFACES∗
2020-06-04
School of Science,Beijing University of Posts and Telecommunications,Beijing 100876,China
E-mail:ymzhong@bupt.edu.cn
Abstract Smillie and Weiss proved that the set of the areas of the minimal triangles of Veech surfaces with area 1 can be arranged as a strictly decreasing sequence{an}.And each anin the sequence corresponds to finitely many affine equivalent classes of Veech surfaces with area 1.In this article,we give an algorithm for calculating the area of the minimal triangles in a Veech surface and prove that the first element of{an}which corresponds to non arithmetic Veech surfaces iswhich is uniquely realized by the area of the minimal triangles of the normalized golden L-shaped translation surface up to affine equivalence.
Key words Veech surfaces;minimal triangles;non arithmetic
1 Introduction
Given a closed Riemann surface X and a holomorphic 1-form ω on X,the pair(X,ω)is called a translation surface.Denote by zero(ω)the set of zeros of ω.It is well known that there is an atlas{(Uα,φα)}α∈Ion X −zero(ω)such thatAs the transition functions of{(Uα,φα)}α∈Iare translations,the Euclidean metric on the plane R2induces a flat metric on X with conical singularities at the points of zero(ω).The points in zero(ω)are called singular points.Sometimes we may need to mark finitely many points,which are not singular points,in a given translation surface.The marked points are called removable singular points and also considered as singular points.Throughout this article,we only consider translation surfaces without removable singular points,except for the flat torus with one marked point.A geodesic between two singular points(which need not be distinct)without singular points in its interior is called a saddle connection.Let θ∈ [0,2π).Denote by Fθthe measured foliation induced by the geodesics in direction θ.In general,the leave of Fθcan be divided into two types.A leaf is called a regular trajectory,if it does not go through any singular points;a leaf is called a critical trajectory,if it emits from a singular point or lands to a singular point.Especially,a closed regular trajectory is called a periodic trajectory and a critical trajectory which emits from a singular point and lands to a singular point is just a saddle connection.The set of all the saddle connections in direction θ is denoted by S(θ)and the set of all the regular trajectories in the direction θ is denoted by R(θ).
An orientation-preserving homeomorphism f:(X,ω)→ (Y,η),which is affine with respect to the local coordinates off the singular points,is called an affine isomorphism.Denoted by a ff(X,ω)the set of affine automorphisms of(X,ω).Particularly,if an affine isomorphism is given by translations with respect to the local coordinates off the singular points,then it is called a translation isomorphism.The set{Df:f ∈ a ff(X,ω)}is called the Veech group of(X,ω),which is denoted by Γ(X,ω).The dynamical properties of geodesics in translation surfaces is a central problem in the study of translation surfaces.In the celebrated article[13],Veech proved that if Γ(X,ω)is a lattice,then the trajectories in(X,ω)satisfy the following dichotomy:Given θ∈ [0,2π),
A translation surface whose Veech group is a lattice is called a Veech surface or a lattice surface.In particular,if the Veech group of a translation surface is commensurable to SL(2,Z),then the translation surface is called arithmetic.All arithmetic translation surfaces are Veech surfaces.The non-arithmetic lattice surfaces are firstly discovered by Veech in[13].As the dynamical properties of geodesics in Veech surfaces are optimal(see[7]),it is an important problem to characterize Veech surfaces.Vorobets considered this problem by using areas of triangles in translation surfaces.A triangle in a translation surface(X,ω)is the image of continuous mapping f from a triangle△ in R2to(X,ω),where f is isometric in the interior of△,the image of the vertice are singular points(which need not be distinct),the image of edges are saddle connections,and f(△)has no singular points in its interior.Let(X,ω)be a translation surface.Denote by A(X,ω)the set of areas of all triangles in(X,ω).Vorobets proved that if A(X,ω)is bounded below by a positive number,then(X,ω)satisfies Veech’s dichotomy,and A(X,ω)is a finite set if and only if(X,ω)is a Veech surface[14].As Veech surfaces imply Veech’s dichotomy,Vorobets asked the question:Whether A(X,ω)is bounded below by a positive number implies that A(X,ω)is a finite set? Smillie and Weiss give a positive answer to this question[10].Let

If(X,ω)is a Veech surface,by using the results of Smillie and Weiss,we see that m(X,ω)=min{A(X,ω)}and m(X,ω)is positive.A triangle △ in a Veech surface(X,ω)is called a minimal triangle,if Area(△)is equal to m(X,ω).Because we need to compare the the areas of minimal triangles in different translation surfaces,we define the normalized area of minimal triangles of a translation surface(X,ω)to be

If the area of a translation surface(X,ω)is 1,we say(X,ω)is a normalized translation surface.Obviously,we haveprovided that(X,ω)is a normalized translation surface.Let A1be the set of all the affine equivalent classes of normalized translation surfaces.Assume that[(X,ω)]be an element of A1.DefineAs any two presentations(X1,ω1)and(X2,ω2)of[(X,ω)]are affine equivalent and with areas 1,it is clear thatandare equal.Thus,is well defined.Let α be a positive number and let V1⊂A1be the set of affine equivalent classes of Veech surfaces with area 1.Define

and

Smillie and Weiss proved that M(α)is a finite set for any given positive number α (see[10]).Therefore,the set A is a countable set and can be listed as a strict decreasing sequence.That is,

where αn> αn+1for all n=1,2,···.Smillie and Weiss also proved that

and all the affine equivalent classes of Veech surfaces corresponding to αi(i=1,2)consists of arithmetic translation surfaces.The number α1corresponds to the flat torus with one marked point and α2corresponds L-shaped translation surface tiled by three squares.In fact,Simllie and Weiss also considered both marked translation surfaces and flat surfaces.There exists a flat surface such that the area of the minimal triangles in it is 1/4[10].In[11],Smillie and Weiss asked the following question:which is the first number in A corresponding to non-arithmetic Veech surfaces?
In this article,we will give an algorithm for calculating the areas of the minimal triangles for some special translation surfaces.Using the algorithm,we proved the following theorem.

Remark 1.2The definition of L-shaped translation will be given in Section 2.

2 Preliminaries
In this section,we recall some basic concepts and results on translation surfaces,which will be used later.
2.1 Billiards in L-shaped polygons and translation surfaces of genus 2
Let P be a simple connected polygon in C.The polygon P is called rational if all its angles are rational multiples of π.Consider an ideal particle which is moving in P with unit speed and satisfies optical reflection rule when it meets the boundary of P.This dynamical system is called a rational billiard.It is well known that the rational polygon P induces a canonical translation surface SPby some unfolding process,see[1]or[6].It is also an important way to obtain some explicit translation surfaces.In particular,by using rational billiards in L-shaped polygon,one can obtained essentially all the Veech surfaces in H(2),where H(2)is all the translation equivalent translation surfaces of genus 2 with only one singular point[7].
Let L be an L-shaped polygon(see Figure 1(a)).Obviously,the polygon L is a rational polygon.Using the unfolding process,we obtain a cross(see Figure 1(b)).After identifying the parallel edges of the cross by translations,the result surface SLis a translation surface of genus 2 with only one singular point.Note that the cross also induces a L-shaped polygon L′(see Figure 1(b)and Figure 1(c)).By identifying the parallel edges,we also obtain a translation surface SL′of genus 2 with only one singular point.It is clear that SL′=SL.

Figure 1 Unfolding an L-shaped billiard table
Let


Figure 2 The L-shaped billiard table L(b,e)and the associated L-shaped polygon
Theorem A(McMullen) For each Veech surface(X,ω)in H(2),there is a unique translation surface S(b,e)such that(X,ω)is affine equivalent to S(b,e),where(b,e)∈ P.
2.2 Some properties of minimal triangles in Veech surfaces
Let(X,ω)be a translation surface.For each(oriented)saddle connection γ,there is a complex number

which is called the holonomy vector of γ.The set of holonomy vectors induced by the set of saddle connections of(X,ω),denoted by Hol(X,ω),is a discrete set in C[14].And the set of directions induced by Hol(X,ω)is dense in[0,2π)[14].For each periodic trajectory c,there is a maximal cylinder C induced by c such that the core curve is c and the boundaries of C consist of saddle connections which are parallel to c.If(X,ω)is a Veech surface andfor a given θ ∈ [0,2π),then(X,ω)is a union of(open)cylinders up to saddle connections(Veech’s dichotomy),where the cylinders are induced by the periodic trajectories in direction θ.In general,if there is a direction θ such that all the regular trajectories in direction θ are periodic,then θ is called a completely periodic direction.
The Veech group Γ(X,ω)of(X,ω)is a discrete subset of SL(2,R)[13].Assume that(X,ω)is a Veech surface.Note that Veech’s dichotomy holds.We see that the set of completely periodic directions of(X,ω)equals the set of saddle connection directions of(X,ω).As Hol(X,ω)is a discrete set,the set of completely periodic directions of(X,ω)is a infinitely countable set.Letbe the set of completely periodic directions of(X,ω),where θn∈ [0,2π)for n=1,2,3,···.We say that two direction θiand θj(i,j ∈ Z+)are equivalent with respect to Γ(X,ω)if there exists an element
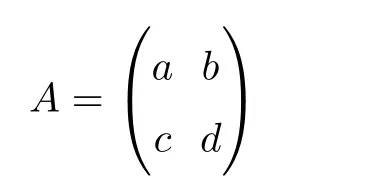
in Γ(X,ω)such that

where λ ∈ R∗.Denote bythe set of equivalent classes induced by the equivalent relationships.We have the following proposition.
Proposition 2.1Let(X,ω)be a Veech surface.Then the setis finite.
ProofBecause(X,ω)is a Veech surface,the Veech group Γ(X,ω)is a non-cocompact lattice[13].Let D be a Dirichlet domain of Γ(X,ω).Then,D has finitely many sides and finitely many vertices at infinity.Let x1,x2,···,xmbe the vertices at infinity of D.Denote the Γ(X,ω)-orbit of xiby Γ(X,ω)xifor i=1,2,···,m.
Because θn∈ Θ is a completely periodic direction and(X,ω)is a Veech surface,there exists a parabolic element Anof SL(2,R)such that cotθnis the fixed point of An(as a möbius tansformation)[13].Therefore,there exists jn∈ {1,2,···,m}such that cotθnis an element of Γ(X,ω)xjn.Thus,there exists

in Γ(X,ω),such that

Assume that xi=cotβi(i=1,2,···,m and βi∈ [0,2π)).Then,

As cn,dn,βjn,and θnare real number,there exists λn∈ R∗such that

It follows that

Therefore,we have

Note that for each i∈ {1,2,···,m},the direction βiis a completely periodic direction of(X,ω)[13].We see that θnis equivalent towith respect to Γ(X,ω).As the setis finite,we see that the setis a finite set.
Let(X,ω)be a Veech surface and D be a Dirichlet domain of Γ(X,ω).Assume that x1,x2,···,xmare the vertices at infinity of D.We say that a direction βi∈ [0,2π)is associated to xi(i=1,2,···,m)if cotβi=xi.The direction βiis a completely periodic direction of(X,ω).From the proof of Proposition 2.1,we have the following corollary.
Corollary 2.2Let D be a Dirichlet domain of Γ(X,ω),where(X,ω)is a Veech surface.Assume that x1,x2,···,xmare the vertices at infinity of D.Then,for each completely periodic direction θ of(X,ω),there exists j ∈ {1,2,···,m}such that θ is equivalent to βjwith respect to Γ(X,ω),where βjis associated to xj.
Let C be a maximal cylinder in a given translation surface(X,ω)and let△ be a triangle in(X,ω).With a slight abuse of notation,we use△ ⊂ C to mean that the interior of△is contained in the interior of C.As C is a maximal cylinder,by definition of triangles in a translation surface,we see that the vertices of△are in the boundaries of C.The following simple observation will also be used later.
Proposition 2.3Let(X,ω)be a Veech surface andThen,there exists a cylinder C in(X,ω)and a triangle△ ⊂ C such that Area(△)=a.
ProofAs(X,ω)is a Veech surface,there exists a triangle △′in(X,ω)such that Area(△′)=a(see[10]).Assuming that △′is not contained in any cylinder,we shall seek a contradiction.
Let s be an edge of△′,then s is a saddle connection in(X,ω).We may choose an orientation of s such that△′lies in the left side of s.As(X,ω)is a Veech surface,there is a cylinder C such that s⊂ ∂C and C lies in the left side of s.Let v′be the vertex which is opposite to s,h′the height from v′to s,and h the height of C.Let v be a singular point in ∂C such that v is opposite to s.Then,v and s determine a triangle△ such that v is a vertex of△,s is an edge of△,and v is opposite to s.Note that h′>h.Consequently,we have Area(△) From Proposition 2.3 and Corollary 2.2,we have the following algorithm. Theorem 2.4Let(X,ω)be a Veech surface and D be a Dirichlet domain of Γ(X,ω).Assume that β1,β2,···,βn(n ∈ Z+)are the completely periodic direction of(X,ω)associated to the vertices at infinity of D.Let(j=1,2,···,j(i)and j(i)∈ Z+)be the maximal cylinder with respect to βi,such thatup to the saddle connections.Assume that the height ofisand the boundaries ofconsists of saddle connectionswhere m(i,j) ∈ Z+.Then,is equal to where j(i)is the number of maximal cylinders with respect to βiand m(i,j)is the number of saddle connections in the boundaries of ProofDenote It follows from Theorem 2.4 that one can calculate the areas of minimal triangles for the Veech surfaces whose Veech groups are known,especially for the Veech surfaces induced by regular polygons[13]. The golden L-shaped translation surface LGis generated by the L-shaped polygon given in Figure 3.Using Theorem 2.4,we obtain the following corollary. ProofIt is well known that the Veech group Γ(LG)is isomorphic to the triangle group(2,5,∞)[4].Thus,one can find a Dirichlet domain R of Γ(LG)such that there is only one vertex x at infinity of R.Note that the horizontal direction is a completely periodic direction of R.Without loss of generality,we may assume that x=∞.There are two cylinder C1and C2in the horizontal direction(see Figure 3),and LG=C1∪C2up to the horizontal saddle connections.To simplify notations,we identify|Hol(si,j)|with si,j.By Theorem 2,we see that Note that Hol(s1,1)=Hol(s1,2),Hol(s2,1)=Hol(s2,3),and Hol(s2,2)=Hol(s2,4).We deduce that Figure 3 The golden L-shaped translation surface In this section,we prove Theorem 1.1.First,we have the following estimates of the areas of minimal triangles in Veech surfaces[10]. Proposition 3.1Let(X,ω)be a translation surface of genus g≥ 1.Assume the number of singular points is v.Then,the area of the minimal trianglessatisfies ProofConsider a triangulation T of(X,ω)such that all the vertices of T are singular points and all the edges are saddle connections.Such a triangulation exists.For example,we may take the Delaunay triangulation of(X,ω)[2,5].Assume that the number of the vertice(resp.edges,faces)of T is v(resp.e,f).Then, As v−e+f=2−2g and 2e=3f,we see that From Proposition 3.1,we have the following corollary. Corollary 3.2The first element in A corresponding to non-arithmetic Veech surfaces can only be realized by normalized Veech surfaces of genus 2 with only one singular point. ProofAs the translation surfaces(with or without singular points)of genus 1 can not be a non-arithmetic surface[3],we only need to consider translation surfaces of genus greater than 1. Assume that(X,ω)is a normalized translation surface of genus g≥ 3.Let v be the number of singular points.It follows form Proposition 3.1 that Assume that(Y,η)is a normalized translation surface of genus g=2.It is well known that the number of singular points of(Y,η)is at least 1.If it is greater than 1,then, The proof of Corollary 3.2 is completed. In order to find the first element in A corresponding to non-arithmetic Veech surfaces,in view of Corollary 3.2,we only need to consider all the translation surfaces in H(2).In the light of McMullen’s theorem(Section 2),we consider the normalized areas of minimal triangles in S(b,e)for all possible parameters b and e.Obviously,the triangles T1(b,e),T2(b,e),and T3(b,e)are triangles in S(b,e).Denote by ai(b,e)the area of Ti(b,e)for i=1,2,3.And the normalized area of Ti(b,e)is We have the following propositions. Proposition 3.3Let ProofObviously,we have It is easy to see that which implies that b= λ2−λe.Thus,Area(S(b,e))=8λ2−4λe,and and Thus,the proposition holds. Thus,we see that Furthermore,by using results of Mukamel[9],one may obtain the precise value ofLet(b,e)=(2,−1).It is easy to see that the translation surface S(2,−1)is affine equivalent to the L-shaped translation surface tiled by three squares.By a result of Smillie and Weiss[10],we have Figure 4 The L-shaped translation surface induced by L(3,−1) Proposition 3.5The following facts hold: ProofWe need to consider the following three cases. Case 1If e=−1,then Case 2If e=0,then b≥ 2 andThus, In particular,if b=2,3,we have if b≥4,then if b≥ 6,then λ ≥ 3,which implies Proof of Theorem 1.1Using Corollary 3.2 and Proposition 2.3,we only need to prove that,for each non-arithmetic Veech surface(X,ω)distinguished from LGin H(2), Using Theorem A,we know that there is a unique pair(b,e)such that(X,ω)is affine isomorphic to S(b,e).Thus,we see that for all admissible pair(b,e)except for(b,e)=(1,−1),(b,e)=(2,−1),and(b,e)=(3,−1).Note that S(1,−1)is affine isomorphic to LGand S(2,−1)is an arithmetic Veech surface.We only need to prove that This is a simple corollary of Proposition 3.3.Hence,the proof of Theorem 1.1 is completed. AcknowledgementsThe author would like to thank Shengjian Wu for helpful discussions and encouragement.
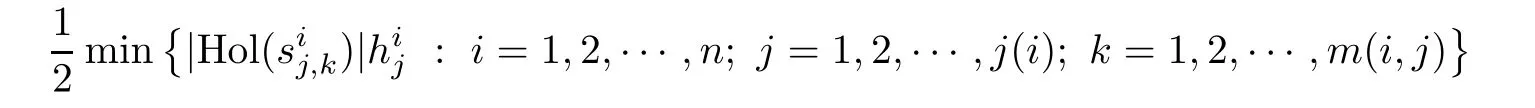

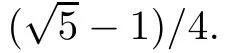


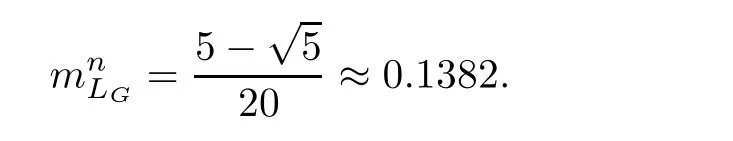

3 Proof of Theorem 1.1

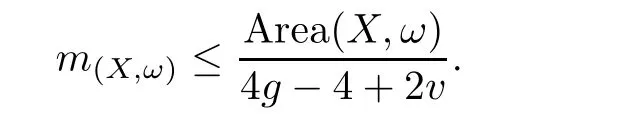
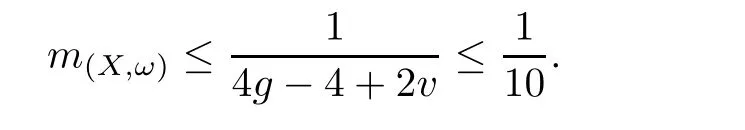











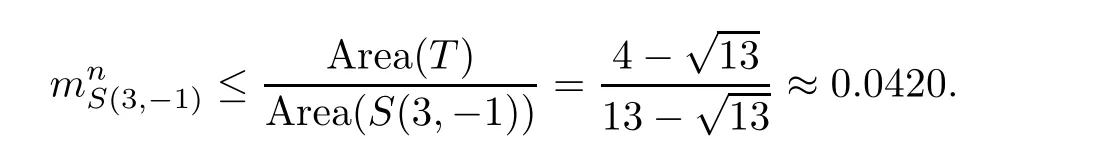

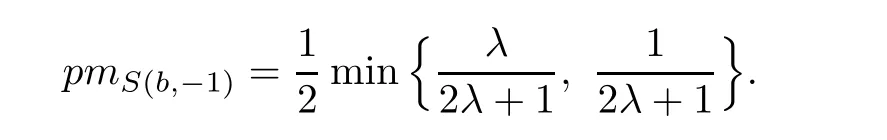





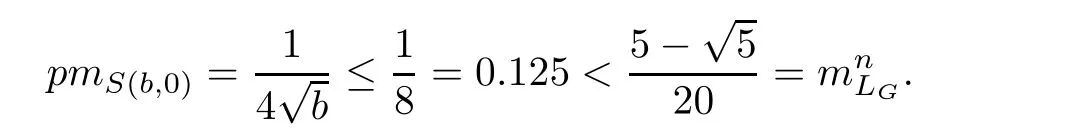


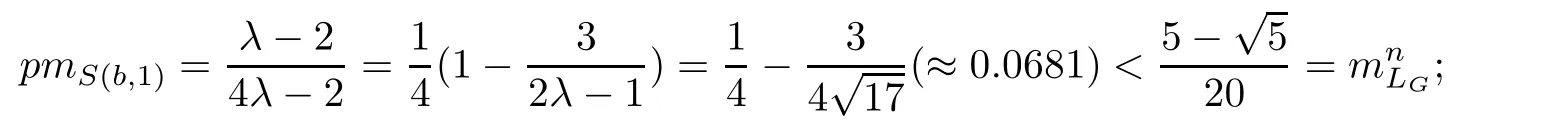

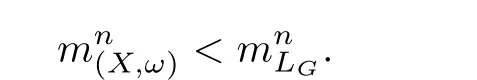



杂志排行
Acta Mathematica Scientia(English Series)的其它文章
- INFINITE SERIES FORMULAE RELATED TO GAUSS AND BAILEY-SUMS∗
- MULTI-BUMP SOLUTIONS FOR NONLINEAR CHOQUARD EQUATION WITH POTENTIAL WELLS AND A GENERAL NONLINEARITY∗
- ASYMPTOTIC BEHAVIOR OF SOLUTION BRANCHES OF NONLOCAL BOUNDARY VALUE PROBLEMS∗
- ASYMPTOTIC DISTRIBUTION IN DIRECTED FINITE WEIGHTED RANDOM GRAPHS WITH AN INCREASING BI-DEGREE SEQUENCE∗
- SOME METRIC AND TOPOLOGICAL PROPERTIES OF NEARLY STRONGLY AND NEARLY VERY CONVEX SPACES∗
- ON THE EXISTENCE OF SOLUTIONS TO A BI-PLANAR MONGE-AMPÈRE EQUATION∗
