LOCAL WELL-POSEDNESS OF STRONG SOLUTIONS FOR THE NONHOMOGENEOUS MHD EQUATIONS WITH A SLIP BOUNDARY CONDITIONS∗
2020-06-04
School of Mathematics and Statistics,Zhumadian Academy of Industry Innovation and Development,Huanghuai University,Zhumadian 463000,China
E-mail:hmlmath@163.com
Yuelong XIAO†
School of Mathematics and Computational Science,Xiangtan University,Xiangtan 411105,China
E-mail:xyl@xtu.edu.cn
Abstract This article is concerned with the 3D nonhomogeneous incompressible magnetohydrodynamics equations with a slip boundary conditions in bounded domain.We obtain weighted estimates of the velocity and magnetic field,and address the issue of local existence and uniqueness of strong solutions with the weaker initial data which contains vacuum states.
Key words Nonhomogeneous MHD equations;local existence and uniqueness;vacuum;t-weighted H2estimate;Galerkin approximation
1 Introduction
In this article,we consider the following nonhomogeneous incompressible MHD system

in Ω × (0,T),where Ω ⊂ R3is a bounded open set with smooth boundary,and T>0.The unknowns ρ,u=(u1,u2,u3),b=(b1,b2,b3),and π denote the density,the velocity field,the magnetic field,and the pressure of the fluid,respectively.
Concerning the nonhomogeneous fluid equations,there exists a considerable number of papers devoted to their mathematical analysis[1,2,4,9–11,19,27,28].It is worth noting that density may play different roles.For compressible fluid,the pressure is commonly expressed as exponential function about the density.Navier-Stokes equations with density-dependent viscosity is considered[17].In[29],Wu studied incompressible magnetohydrodynamic equations with the coefficients depending on the density and temperature.In general,the initial vacuum is taken into consideration;for instance,see[7,11,23,24].Li[22]considered 3D nonhomogeneous incompressible magnetohydrodynamic equations with density-dependent viscosity and resistivity coefficients,and the vacuum of initial density was also allowed.
Because of its mathematical challenges and physical complexity,rich phenomena,MHD has been the important subject of many studies by mathematicians and physicists;see[5,6,8,12,14,21,26,30,32]and the references cited therein.Global well-posedness of threedimensional incompressible magneto-hydrodynamical system with small and smooth initial data in whole space was established by Xu and Zhang in[33].The authors in[34]studied the 3D incompressible MHD equations with density-dependent viscosity,and obtained global strong solutions under the assumption that the initial energy was suitably small.Unique global strong solution of the 2D MHD problem with boundary conditions
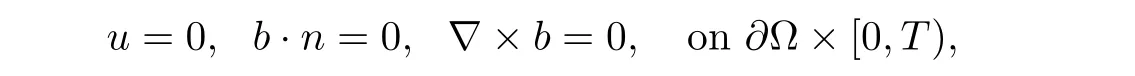
is studied by Huang,as the viscosity µ = µ(ρ)is a function in C1(0,∞),seeing[16].In[7],the authors obtained the strong solution of incompressible magnetohydrodynamic equations(1.1)–(1.4),with boundary conditions

and the initial data satisfy that

and the compatibility conditions

for some(p0,g)∈H1×L2.
In bounded domain,various boundary conditions were proposed.Generally,n and τ denote the outward normal vector and the unit tangential vector on∂Ω,respectively.The classical noslip boundary condition,u=0 on∂Ω,which gives rise to the phenomenon of strong boundary layers.Later,Xiao and Xin[31]obtained a unique strong solution of the 3D incompressible Navier-Stokes equations with a slip boundary condition,u·n= ∇×u·τ=0 on∂Ω,and proved strong convergence for the vanishing viscosity limit inflat case.Guo and Wang studied the similar problem for MHD system with generalized Navier slip boundary conditions,u·n=0 and n × (∇ × u)=[βu]τon ∂Ω,where β is a given smooth symmetric tensor on the boundary[13].For nonhomogeneous fluid,under slip boundary condition,this is quite difficult to get a strong solution because of variable density.Thus,we supplement the system with initial and boundary conditions:

It is remarkable that Jiu,Wang,and Xin[18]established a unique global classical solution which may contain vacuums to compressible Navier-Stokes equations in weighted spaces.We investigate the existence and uniqueness of strong solutions for system(1.1)–(1.6)in 3D smooth bounded domains.The motivation of the t-weighted estimate originate from the study of several incompressible models,to weaken the regularity of the initial data;see[25].Moreover,it is worth noting that we do not need the compatibility of initial data.We only assume that the initial data satisfy

The article is arranged as follows:In Section 2,we brie fly recall the notations,some lemmas,and main results for the system.Next,in Section 3,we will obtain some prior estimates.Finally,in Section 4,we show Theorem 2.3.
2 Preliminaries and Main Results
In this section,we introduce some notations,which are used throughout this article,definition,main result,and preliminary facts.We use standard notations for Lebesgue and Sobolev spaces.We denote bythe norm in Lp(Ω),and for simplicity,useto denoteMoreoveralso,use Hmto denote Wm,2.As usual,we will use the same notation for vector valued and scalar valued spaces without danger of confusion.Spacesandare the closures of the spacein L2and H1,respectively.
Strong solutions to system(1.1)–(1.6)are defined as follows.
Definition 2.1Given a positive time T ∈ (0,∞),and the initial data(ρ0,u0,b0)satisfying(1.7),then(ρ,u,b,π)is called a strong solution to system(1.1)–(1.6),on Ω × (0,T),if it has the regularities

satisfying system(1.1)–(1.6)a.e.in Ω × (0,T).

Our aim is to prove the following theorem:
Theorem 2.3Let Ω ⊂R3be a bounded domain with smooth boundary.Assume that the initial data(ρ0,u0,b0)satisfies(1.7).Then,there is a positive time T0,depending only on,andsuch that system(1.1)–(1.6)admits a strong solution(ρ,u,b)on Ω×(0,T0).Moreover,if p∈[2,∞),then the strong solution is unique.
Remark 2.4In fact,the positive time T0also depends on the viscosity-resistivity coefficient,so we just assume that the viscosity-resistivity coefficients are both 1.
Now,we introduce the following lemmas to be needed later on.
Lemma 2.5([20]) Let v∈ L1(0,T;Lip)a vector field,such that∇·v=0,and v·n=0 on ∂Ω.Let ρ0∈ W1,q,with q ∈ [1,∞].
Then,the following system

Moveover,the following estimate holds:

for any t∈[0,T].
Lemma 2.6([3]) Let Ω satisfy the assumptions made in Section 1.Then,the following inequality holds true for all 1 for each divergence-free vector field f ∈ W1,p(Ω)such that either the boundary conditionis satisfied. Lemma 2.7([23]) Given a positive time T,let f,g,G be nonnegative functions on[0,T],with f and g being absolutely continuous on[0,T].Suppose that a.e.on(0,T),where A is a positive constant,and α and β are two nonnegative functions,satisfying Then,the following estimates hold: for t∈[0,T],which,in particular,imply that f≡0,g≡0,and G≡0,provided g(0)=0. In this section,we construct approximate solutions via a Galerkin scheme to system(1.1)–(1.4).We first introduce the approximation scheme,then show the existence of the approximate solutions,and finally derive uniform bounds to be used in next section. Suppose that Ω is simply connected,as in[32],Xmis defined by which is finite-dimensional subspaces of basic function space Then,consider the functions wj∈X satisfying These functions wjmake up a suitable orthogonal system of smooth functions in the sense of the following scalar product on X,and are dense in X: We will solve the following system: for all w,ψ ∈ Xm,where um(0),bm(0)are given by Applying the results in[23],for any v∈C([0,T];Xm),the following problem possesses a unique solution Next,for any v∈C([0,T];Xm),we consider following system which is a linear parabolic-type problem,hence the existence of a solution can be obtained by the standard Galerkin methods.From the results in[15],we obtain the unique solution bm∈Y of problem(3.8),hereand the solution operatoras bm=S[v]is continuous with respect to v∈C([0,T];Xm). In order to prove the solvability of system(3.1)–(3.4),it suffices to find a solution um∈C([0,T];Xm)to the following system We first study the solvability of system(3.9).Givenand ρm=R[v]and bm=S[v],as defined before,thenandand(3.9)is equivalent to Next,we discuss some properties of operator Q defined as before.Taking w=umin(3.9),and noticing that the L∞norm is equivalent to the normis a finite dimensional Banach space,then it follows from integration by parts and using equation(3.7)that Using a generalized Gronwall lemma[27],we can obtain Clearly,umis bounded infrom bm∈ Y.Thus,because ofandwe infer that{cj}is bounded in C([0,T]).This implies that umis bounded(independent of v)in C([0,T];Xm).Moreover,if v is bounded in C([0,T];Xm),from(3.10)and the symmetry ofthe setis bounded in C([0,T])which implies thatis bounded in C([0,T];Xm).Thus,we conclude that there are K1,K2>0 such thatDenote by B1the closed ball in C([0,T];X)of radio K1,and B2the closed ball in C1([0,T];Xm)of radio K2.Then,the mapping Q is continuous from B1to B2.The Arzelà-Ascoli theorem implies that B2is compact in C([0,T];Xm).And therefore Q is continuous and compact mapping from B1into B2,and by the Schauder fixed point theorem,there is a fixed point umfor a given T>0.Taking ρm,bmas the corresponding solution of(3.7)and(3.8),respectively,we obtain a unique solutions(ρm,um,bm)of(3.1)–(3.4). In this subsection,we will derive some a priori estimates,which are uniform in m,in a short time,to the solution(ρm,um,bm)as above.Now,we study the H1estimate,that is the following proposition: Proposition 3.1Let(ρm,um,bm)be the solution of system(3.1)–(3.4).Then,there is a positive time T0depending only onand k(u0,b0)k,such that for a positive constant C depending only onand ProofTaking w= ∂tumin(3.2)andin(3.3),then it follows from integration by parts and the Young’s inequality that and thus Applying the H2estimate to(3.2)and(3.3),we deduce where M and C are positive constants depending only onand Ω.Multiplying(3.11)by 2M,and summing the resultants with(3.12)and(3.13),we obtain for a positive constant C depending only on ρ and Ω.Noticing that similarly, which,substituted into(3.14),gives for a positive constant C depending only onand Ω. Set Then,it follows from(3.15)that where C1is a positive constant depending only on ρ and Ω.By ordinary differential inequality,we find that there is time T0>0,such that This completes the proof of Proposition 3.1. Next,we can work on the t-weighted H2estimate,which is stated in the following proposition. Proposition 3.2Let(ρm,um,bm)be the solution of system(3.1)–(3.4)and T0the number in Proposition 3.1.Then,the following estimate holds for a positive constant C depending only onand ProofDifferentiating(3.2)and(3.3)with respect to t yield for all w,ψ ∈ Xm.Taking w= ∂tumand ψ = ∂tbmin the above equalities respectively,then it follows from integration by parts and using(3.1)that Substituting the estimates on Ii,i=1,2,···,7,into(3.16),and using the Young inequality,one obtains which implies Multiplying the above inequality by t yields By the Gronwall’s inequality,and using Proposition 3.1,we obtain for a positive constant C depending only onand for a positive constant C depending only on,and Ω,which along with(3.17)completes the proof of Proposition 3.2. This section is devoted to proving Theorem 2.3,We start with the following result. Proposition 4.1Suppose that the initial datafor some p∈[1,∞),and thatand T0stated in Proposition 3.1.Then,there is a strong solution(ρ,u,b)to system(1.1)–(1.4),subject to(1.5)–(1.6),in Ω × (0,T0),such thatand for a positive constant C depending only onand ProofChoose a sequence ofsuch that By Propositions 3.1–3.2,for any positive integer m,there is a solution(ρm,um,bm)to system(3.1)–(3.4),such thatand where T0is the positive time stated in Proposition 3.1,and C is a positive constant depending only onT0,Ω,and Because of the above estimate,there exists a subsequence ofstill denoted byand a triple(ρ,u,b),withand for a positive constant C depending only onandsuch that By the previous convergences,it is clear that(ρ,u,b)satisfies(1.1)–(1.4),in the sense of distribution,and moreover,because ρ ∈ L∞(0,T0;W1,p)and ∂tρ ∈ L4(0,T0;Lp),which will be proven in the below,(ρ,u,b)satisfies equations(1.1)–(1.4)a.e.in Ω × (0,T0).The previous convergences also imply that Consequently,as m→∞in(3.2),by integration by parts,we deduce that Noticing that Next,one still need to verify By the elliptic estimate and using the Sobolev inequality,we deduce similarly, and thus,recalling(4.1),we obtain for a positive constant C depending only on,and for a positive constant C as above.Applying Lemma 2.5,it follows that for a positive constant C depending only on,and.It follows from the continuity equation(1.1)that for a positive constant C as above.This completes the proof of Proposition 4.1. Finally,we are ready to prove Theorem 2.3. ProofTake a sequence,such that By Proposition 4.1,there is a positive constant T0depending only onandsuch that for each n,there is a strong solution(ρn,un,bn)to system(1.1)–(1.4),subject to(1.5)–(1.6),with initial data(ρ0n,u0n,b0n),in Ω ×(0,T0),satisfyingand for a positive constant C depending only onand Because of the above estimates,by the Cantor diagonal argument,there is a subsequence ofstill denoted by{(ρn,un,bn)},and a triplesuch that Similar to the results in[23],we conclude that(ρ,u,b)has the regularities stated in Theorem 2.3 and satisfies system(1.1)–(1.4)in Ω × (0,T0).Thus,the existence part of Theorem 2.3 is proved. We now prove the uniqueness part of Theorem 2.3.Let(ρ1,u1,b1)and(ρ2,u2,b2)be two local strong solutions to system(1.1)–(1.4),subject to(1.5)–(1.6),on Ω × (0,T),for a positive time T,with the same initial data(ρ0,u0,b0).Then,we have following regularities: Let ρ = ρ1− ρ2,u=u1−u2,and b=b1−b2.Thus,ρ,u,and b satisfy a.e.in Ω×(0,T). Multiplying equations(4.5)by u,and(4.6)by b and using equation(4.4),it follows from integration by parts,the Hölder,Sobolev,Poincaré and Young’s inequalities that namely, where Recalling(4.3),it is clear that α ∈ L1((0,T))and tβ(t)∈ L1((0,T)).From[23],we also get



3 Galerkin Approximation
3.1 The scheme

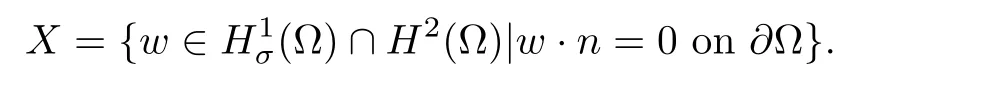
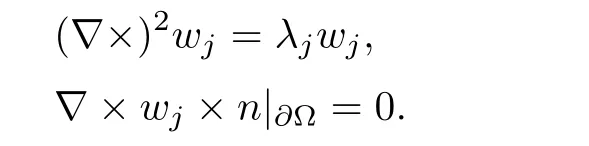








3.2 Solvability of approximated system





3.3 Uniform estimates


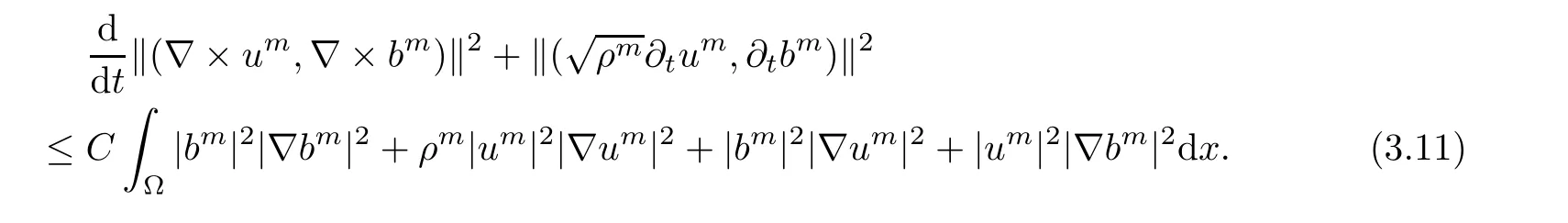






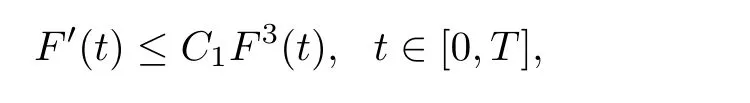
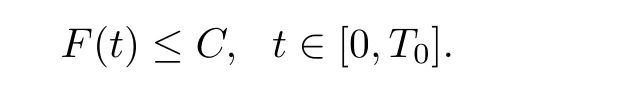










4 Existence and Uniqueness of Solution









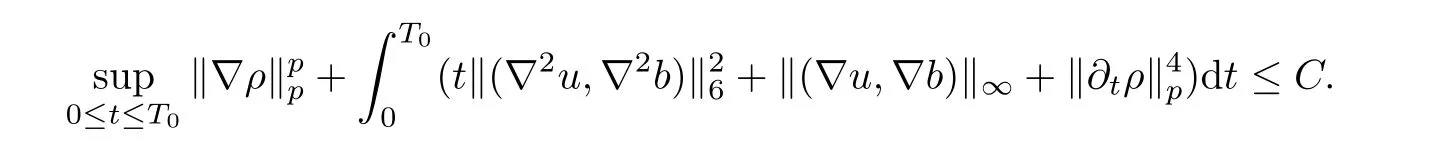



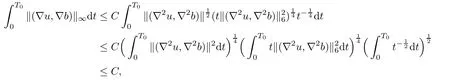






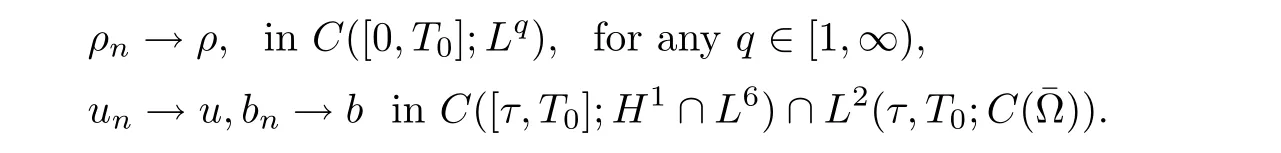
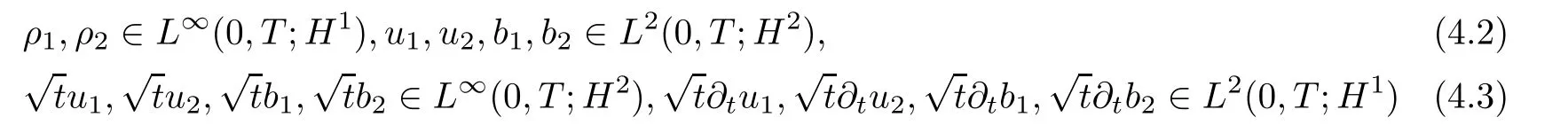


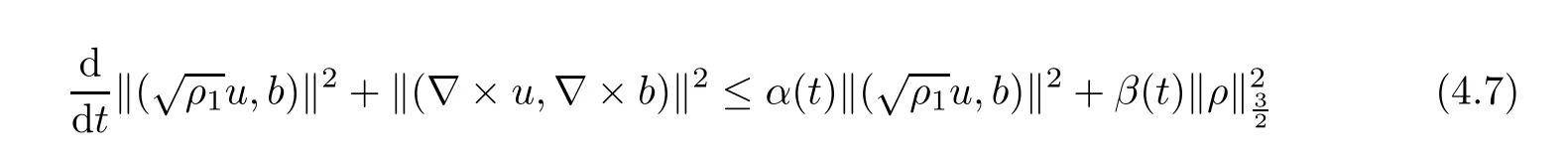
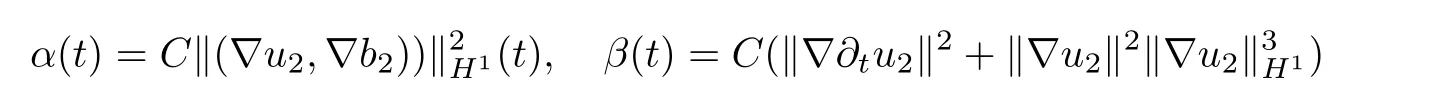

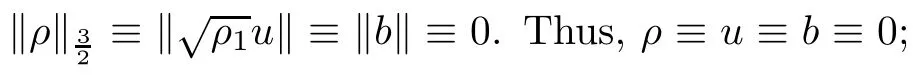
杂志排行
Acta Mathematica Scientia(English Series)的其它文章
- INFINITE SERIES FORMULAE RELATED TO GAUSS AND BAILEY-SUMS∗
- MULTI-BUMP SOLUTIONS FOR NONLINEAR CHOQUARD EQUATION WITH POTENTIAL WELLS AND A GENERAL NONLINEARITY∗
- ASYMPTOTIC BEHAVIOR OF SOLUTION BRANCHES OF NONLOCAL BOUNDARY VALUE PROBLEMS∗
- ASYMPTOTIC DISTRIBUTION IN DIRECTED FINITE WEIGHTED RANDOM GRAPHS WITH AN INCREASING BI-DEGREE SEQUENCE∗
- SOME METRIC AND TOPOLOGICAL PROPERTIES OF NEARLY STRONGLY AND NEARLY VERY CONVEX SPACES∗
- ON THE EXISTENCE OF SOLUTIONS TO A BI-PLANAR MONGE-AMPÈRE EQUATION∗
