APPROXIMATE CONTROLLABILITY RESULTS FOR INTEGRO-QUASILINEAR EVOLUTION EQUATIONS VIA TRAJECTORY REACHABLE SETS∗
2020-06-04Vinodkumar
A.Vinodkumar
Department of Mathematics,Amrita School of Engineering,Amrita Vishwa Vidyapeetham,Coimbatore-641 112,India
E-mail:vinod026@gmail.com;a vinodkumar@cb.amrita.edu
C.Loganathan
Department of Mathematics,Maharaja Arts and Science College,Coimbatore-641 407,Tamil Nadu,India
E-mail:clogu@rediffmail.com
S.Vijay
Department of Mathematics,Government Arts College,Udhagamandalam-643002,Tamil Nadu,India
E-mail:vijay ms oty@yahoo.co.in
Abstract In this article,we study the approximate controllability results for an integroquasilinear evolution equation with random impulsive moments under sufficient conditions.The results are obtained by the theory of C0semigroup of bounded linear operators on evolution equations and using trajectory reachable sets.Finally,we generalize the results too with and without fixed type impulsive moments.
Key words Integro-quasilinear control system;random impulses;approximate controllability
1 Introduction
There is a number of literature in the study of approximate controllability and quasilinear evolution equation and it plays an important role in science and engineering.Only limited attention is given to the study of the existence and controllability results of the quasilinear evolution equation.In articles[11,20],it is found that exact controllability for abstract differential systems is absent in infinite-dimensional space X,when the operator B is compact or the C0semigroup T(t)is compact.This turns our attention to the study of approximate controllability results in infinite-dimensional space X.For further study on approximate controllability and quasilinear evolution equation results,one can see[1,5–10,13–16,18,19,26,27]and the reference therein.
The processes of short-term perturbations can be modeled by an impulsive system.Various study of impulsive systems exists in the history;see[12,17].Most of the papers deal the problem with fixed time impulses,but in a real-time situation,it need not be.The nature of random time on impulse leads the solutions to be a stochastic process.Thus,the random impulsive system gives more realistic than the deterministic impulsive system.In[2],the author detailed the stabilization nature for random impulsive moments in differential equations with exponential distribution.The inaccuracy infinding expectation for the solution x(t)of the random impulsive differential systems[3,4,21–24]is rectified in this article.
The main purpose of this article is to study the approximate controllability of random impulsive integro-quasilinear control systems.In the existed literature,the approximate controllability results were studied using the fixed point theory,compactness of S(t),and uniform boundness for nonlinear term f.We relaxed the condition of compactness and uniform boundness in our proof.Furthermore,we use trajectory reachable set concept from[8,13,14,16,18,19]and the reference therein.We extend the results with and without fixed impulsive terms in integro-quasilinear control systems to fill the gap in the approximate controllability of abstract control systems.To the best of our knowledge,there is no paper which studies the random impulsive integro-quasilinear control systems.
This article is organized as follows:In Section 2,we recall brie fly the notations,definitions,and preliminary facts that are used throughout this article.In Section 3,we study the existence and uniqueness result for random impulsive integro-quasilinear systems.In Section 4,we study the approximate controllability of random impulsive linear control systems and the approximate controllability of random impulsive integro-quasilinear control systems.Furthermore,we extend our results to fixed type impulsive integro-quasilinear control systems and integro-quasilinear control systems.Finally,in Section 5,an example is given to illustrate our results.
2 Preliminaries
Let X and Y be two real separable Hilbert spaces such thatis dense and continuous and Ω be is a nonempty set.Assume thatis a sequence of independent exponentially distributed random variable with parameter λ,and each random variable τk,k=1,2,···is defined from Ω toLet τ,T ∈ ℜ be two constants satisfying τ We consider integro-quasilinear control system with random impulses of the form where A(t,x)is a closed linear operator defined on a dense domain in X and A(t,x)generates an evolution operator inis the set of piecewise continuous functions mappinginto X with some given r>0;u belonging to L2[t0,T;U]is the control function.Letand Y=L2[t0,T;U]be function spaces,be a bounded linear operator,and xtbe a function when t is fixed,defined by xt(s)=x(t+s)for all s ∈ [−r,0].The impulse moments{ξk}form a strictly increasing sequence of random variables,that is,t0= ξ0< ξ1< ξ2< ···< ξk< ···T;for convenience,we take ξ0=t0and ξk= ξk−1+τkfor all k=1,2,···,here t0∈ ℜτis arbitrary given real number;for each k=1,2,···;according to their paths with the normfor each t satisfying t≥ t0,is any given norm in X;ϕ is a function defined from[−r,0]to X,and∆ denotes the set{(t,s):0≤s≤t<∞}. The simple counting process is denoted asand it is generated by{ξn},that is,and denote Ftthe σ-algebra generated by.Then,is a probability space.Let L2=L2(Ω,Ft,X)denote the Hilbert space of all Ft-measurable square integrable random variables with values in X. Assume that T>t0is any fixed time to be determined later and let B denote the Banach space B?[t0−r,T],L2?,the family of all Ft-measurable,C-valued random variables ψ with the norm Remark 2.1For any given time t>0 and integer n ≥ 1,ξnandare related by.It is understood that,{ξn≤ t}is the event that the ntharrival occurs by time t,implies that,the number of arrivals by time t,must be at least n.Similarly,implies{ξn≤ t},yielding the equality.The counting processis a stochastic process in time.The given filtration Ftrepresents the evolution of knowledge about the random system through time.The information at time t carried by filtration Ftdetermines the value of the random variable ξk. Remark 2.3From[2,25],expected value of the solution x(t)for the random impulsive differential equations are given as where the impulse moments ξk,k=1,2,···,follow exponential distribution with parameter λ. The following definition here for the evolution family of operators.For further read on quasilinear operator and evolution operator,see monograph[1,7,15]and the references therein. Definition 2.4A two parameter family of bounded linear operators S(t,s),t≥s≥0,on X is called an evolution system if (i)S(s,s)=I and S(t,r)S(r,s)=S(t,s),t≥r≥s≥0; (ii)(t,s)→S(t,s)is strongly continuous for t≥s≥0. From[15],for the family{A(t,w),(t,w)∈[t0,T]×X}of operators,there exists an evolution system Sh(t,s)in X satisfying,for any fixed h∈B,that Let us consider quasi-linear differential equations with random impulses of the form Definition 3.1For a given T∈(t0,+∞),a stochastic process{x(t)∈B,t0−r≤t≤T}is said to be a mild solutions to equation(3.1)–(3.3)in(Ω,P,{Ft}),if (i)x(t)∈ B is piecewise continuous and Ft−adapted for t∈ [t0,T); Now,we introduce following hypotheses used in our discussion: (H1)The function F:[t0,T]×[t0,T]×C→X is continuous and it satisfies the Lipschitz continuous with respect to x,that is, (H2) (H3) Theorem 3.2Assume that hypotheses(H1)–(H3)is hold.Then,the system(3.1)–(3.3)has unique mild solution on[−r,T]. ProofLet T be an arbitrary number T>t0,such that In order to apply the contraction principle,we define the nonlinear operator Φ :B → B as follows: and for t∈[t0,T], It is easy to prove the continuity of Φ.Now,we have to show that Φ is a contraction mapping.For any x,y∈B,we have By(H3)and Lemma 2.2, noting that therefore,equation(3.6)becomes therefore, Hence, By(3.5),we get Λ(T)<1. Then,we can take a suitable 0 Definition 4.1If for any ǫ>0 and the initial function ϕ ∈ C,there exist a control u ∈ Y such that the mild solution x(·)of(2.1)–(2.3)satisfies then control system(2.1)–(2.3)is said to be approximately controllable on[t0,T]. Let xt(ϕ(t0),u)be the state value of system(2.1)–(2.3),which corresponds to the control u ∈ Y at time t with the initial value ϕ(t0).The set of all possible trajectories,denoted by is called the trajectory reachable set of system(2.1).In particular,the reachable set of system(2.1)–(2.3)at terminal time T is defined by Now,we give the following definitions: (ii)The continuous operator Q fromto C([t0,T],X)is The mild solution for control system(2.1)–(2.3)can be written as follows: Definition 4.2For a given T∈(t0,+∞),a stochastic process{x(t)∈B,t0−r≤t≤T}is said to be a mild solution to equation(2.1)–(2.3)in(Ω,P,{Ft}),if (i)x(t)∈B is piecewise continuous and Ft-adapted for t∈[t0,T); Now,we introduce additional hypotheses used in the following discussion: (H4)For any given ǫ>0 and p(·) ∈ Z,there exists some control u(·) ∈ Y such that In the following lemma,we prove the approximate controllability of the linear system of the form By assumption(H4),for any given ǫ>0,there exists some control u(·) ∈ Y such that In the following theorem,we prove the approximate controllability of the integro-quasilinear control system(2.1)–(2.3) ProofLetting x(·)∈ Kα(0),there exists a u ∈ Y,which can be written as for t∈[t0,T], Now,let y(t)be mild solution of(2.1)–(2.3)corresponding to the control u−w,then Taking supremum over t and by Grownwall’s inequality,we get Corollary 4.5Under the assumption of the above theorem,system(2.1)–(2.3)is approximately controllable. ProofThe proof is a particular case of Theorem 4.4 at α=T. The following remark generalize system(2.1)–(2.3)with fixed impulsive system under sufficient condition. Remark 4.6If the impulses exist at fixed times in system(2.1)–(2.3),then by the similar argument as in Corollary 4.5,system(2.1)–(2.3)is approximately controllable. When there is no impulse condition,then problem becomes abstract integro-quasilinear differential equations with delays that Remark 4.7If there is no impulses,then the system(2.1)–(2.3)becomes that Theorem 4.8Let hypotheses(H1)–(H2)and(H4)–(H5)be hold.Then,system(4.9)–(4.10)is approximately controllable. ProofThe proof is a particular case of Theorem 4.4 at α=T. Example 5.1Consider the following integro partial differential control systems with random impulses of the form where µ >0 and q is a function offoris an arbitrarily given real number; τiand τjare independent with each other asfor i,j=1,2,···and follow exponentially distributed random variable with parameter λ. For every reals s,we introduce a Hilbert space Hs(R)as follows[15].Let the linear space functions z∈L2(R)andis the Fourier transform of z,then Let the linear space functionswith the inner product be defined as Denote Hilbert space Hs(R)with respect to the norm.From this,it is clear that H0(R)=L2(R). Let us consider X=U=H0(R)=L2(R)and Y=Hs(R),s≥3.Define an operator A0by D(A0)=H3(R)and A0z=D3z for z∈D(A0)where D=d/dx.Then,A0is the infinitesimal generator of a C0group of isometries on X.Now,we define,for every ν∈Y,an operator A1(ν)by D(A1(ν))=H1(R)and z ∈ D(A1(ν)),A1(ν)z= νDz.Then,for every ν ∈ Y,the operator A(ν)=A0+A1(ν)is the infintesimal generator of C0semigroup Sx(t,0)on X satisfyingfor everywhere c is a constant independent of ν∈Y.Let Brbe the ball of radius r>0 in Y and it is proved that the family of operators A(ν),ν ∈ Br,satisfies the conditions of definition(2.4)and H2(see[15]). We assume that the following conditions hold: Assume that condition(i)is verified,and(H1)holds,then problem(5.1)can be modeled as the abstract form of equations(2.1)by defining Proposition 5.2Let hypotheses(H1)–(H5)be hold.Then,the mild solution z of system(5.1)is approximately controllable. ProofCondition(i)implies that(H3)holds AcknowledgementsThe authors sincerely thank the Professor R.P.Agarwal,Department of Mathematics,Texas AM University-Kingsville,Kingsville,for his careful reading,constructive comments and fruitful suggestions to improve the quality of the manuscript.




3 Existence and Uniqueness



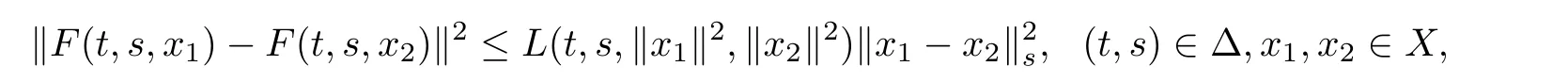





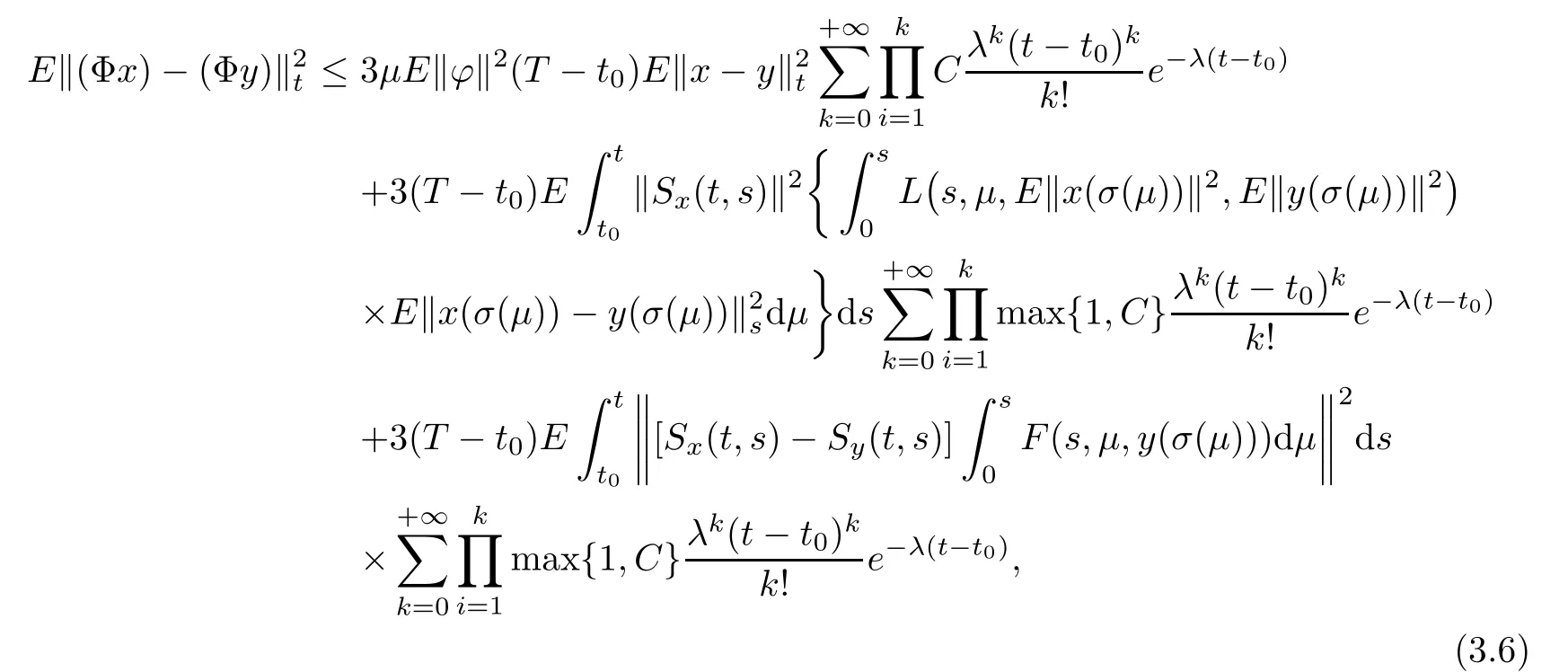




4 Approximate Controllability


















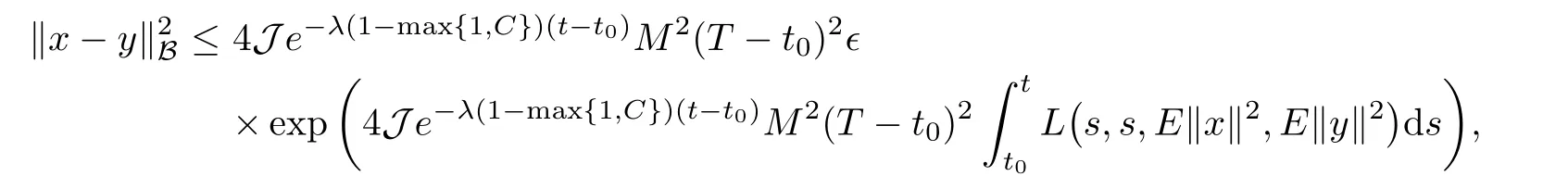

5 An Example





杂志排行
Acta Mathematica Scientia(English Series)的其它文章
- INFINITE SERIES FORMULAE RELATED TO GAUSS AND BAILEY-SUMS∗
- MULTI-BUMP SOLUTIONS FOR NONLINEAR CHOQUARD EQUATION WITH POTENTIAL WELLS AND A GENERAL NONLINEARITY∗
- ASYMPTOTIC BEHAVIOR OF SOLUTION BRANCHES OF NONLOCAL BOUNDARY VALUE PROBLEMS∗
- ASYMPTOTIC DISTRIBUTION IN DIRECTED FINITE WEIGHTED RANDOM GRAPHS WITH AN INCREASING BI-DEGREE SEQUENCE∗
- SOME METRIC AND TOPOLOGICAL PROPERTIES OF NEARLY STRONGLY AND NEARLY VERY CONVEX SPACES∗
- ON THE EXISTENCE OF SOLUTIONS TO A BI-PLANAR MONGE-AMPÈRE EQUATION∗
