基于三维视角的农业干旱对气象干旱的时空响应关系

冯 凯，粟晓玲

基于三维视角的农业干旱对气象干旱的时空响应关系

冯 凯，粟晓玲※

（1. 西北农林科技大学水利与建筑工程学院，杨凌 712100；2. 西北农林科技大学旱区农业水土工程教育部重点实验室，杨凌 712100）

气象干旱是农业干旱的驱动因素，研究农业干旱对气象干旱的响应特征对理解干旱演变机制具有重要作用，而以往研究大多忽略了干旱的时空连续特征。该研究以SPEI和aSPI分别表征气象干旱和农业干旱，基于三维干旱识别方法提取2类干旱的历时、面积、烈度、强度、中心以及迁移距离6个干旱特征，分析黑河流域1961－2014年干旱时空连续动态演变特征；提出时空尺度干旱事件匹配准则，确定存在时空联系的气象-农业干旱事件，探讨气象、农业干旱时空响应特征并建立干旱特征响应模型。结果表明：1）从三维视角可准确全面地认识干旱事件时空动态演变过程及区域干旱发展规律，研究区秋冬春连旱一般起源于中游中部，沿东南方向逐渐向上游迁移并消亡，且干旱迁移速率在上游相对较快；2）基于时空尺度的干旱事件对匹配结果能够保证时空尺度上气象、农业干旱的复杂关系更接近实际，为准确分析气象-农业干旱时空响应特征提供保障；3）研究区气象-农业干旱历时、干旱面积和干旱烈度的最优响应模型分别为二次多项式、指数函数和指数函数。该研究为准确评估干旱时空动态演变规律及干旱响应关系提供了新思路。

干旱；气象；农业；动态演变；干旱匹配

0 引 言

由于全球气候持续变暖，近年来高强度的极端气候事件频繁发生[1]。干旱是一种由降水异常减少或水分收支不平衡引发的极端自然灾害，其发展过程缓慢、持续时间长且影响范围广，在世界各地均有发生[2-3]。干旱一旦发生，对生态环境、水资源安全以及社会经济造成严重威胁[4-5]。因此，干旱监测及其演变规律研究对抗旱减灾和水资源管理具有重要意义。

国内外关于干旱时空演变特征（如干旱趋势、强度、频率、干旱面积）的研究已取得一些成果。如詹存等[6]基于标准降水指数（SPI，Standardized Precipitation Index）分析了川中丘陵区1960－2011年季节性干旱时间变化趋势及干旱频率空间分布特征；李斌等[7]从时间和空间尺度分析了1971－2013年陕西省干旱强度、频率及干旱面积变化特征；Corzo等[8]利用非连续和连续两种干旱面积分析方法来提取大尺度干旱事件的时空特征，为干旱的空间分析提供了重要参考；Zhai等[9]基于强度-面积-历时曲线分析了特定时期干旱强度与干旱面积的关系以及干旱的空间变化特征；Andreadis等[10]使用简单的聚类方法识别干旱事件来描述干旱特征的时空变化。但上述研究多局限于分析某一特定区域干旱特征的一维时间变化趋势或某一特定时期的二维空间变化规律，忽略了干旱演变的时空连续性。而干旱实质上是一个时空连续的三维动态演变过程，具有多属性、多尺度的特点[11]，从三维视角（时间-经度-纬度）定量分析干旱事件全过程在连续时空尺度下的演变特征及区域干旱事件发展规律至关重要。

根据不同的水资源供需关系，干旱通常分为气象干旱、农业干旱、水文干旱和社会经济干旱4类[12]。自然状态下，气象干旱是驱动农业、水文干旱形成的唯一外在因素。持续的气象干旱导致土壤含水量降低，河道径流减少，如果补给不及时或补给不足，则诱发农业干旱或水文干旱[13]。研究农业、水文干旱对气象干旱的响应关系及干旱演进机制对干旱评估和预测十分重要。李运刚等[14]采用相关系数法分析了云南红河流域水文干旱对气象干旱的响应特征，结果表明水文干旱滞后气象干旱1－8个月，并建立了气象和水文干旱对应干旱特征之间的线性关系；胡彩虹等[15]基于不同类型的干旱指标分析气象、农业和水文干旱之间的关系表明不同类型干旱间存在一定的时滞关系。国内外类似的研究已开展许多[16-19]，这些研究都是通过不同类型干旱指数之间的相关系数来反映他们在时间上的滞后关系。吴杰峰等[20]研究表明Logarithm 函数模型中的三参数对数形式能够较好地反映晋江流域水文干旱和气象干旱特征之间的关系。上述研究仅考虑了干旱的时间特征（如干旱历时、烈度），而忽略了空间联系，不能全面反映不同类型干旱间的时空响应关系。此外，三维视角下不同类型干旱间传递过程十分复杂，如一场影响面积较大的气象干旱诱发多场小面积农业干旱或者多场小面积气象干旱同时引发一场农业干旱[21]。因此，在构建气象、农业干旱间响应关系之前，有必要对具有时空联系的气象、农业干旱事件进行匹配，保证气象、农业干旱在时空尺度上的错综复杂关系更接近实际状况。

本文基于三维干旱识别方法提取1962－2014年黑河流域中上游气象和农业干旱事件，分析单场干旱事件的连续时空动态演变过程及区域干旱发展规律，而后从时空尺度匹配相关联的气象-农业干旱事件对，分析气象、农业干旱时空响应特征并建立干旱特征响应模型，全面分析气象、农业干旱间的响应关系。

1 研究区概况及数据处理

1.1 研究区概况

黑河流域位于河西走廊中部，是中国西北地区第二大内陆河[22]。流域上莺落峡和正义峡2个控制水文站将流域分为上、中、下游。上游以牧业为主，中游以农业为主，该地区发生干旱会造成草地退化、草地沙化以及作物减产等问题。因此，本文将黑河流域中上游确定为研究区进行农业干旱研究，有助于该地区的灾害防治及水资源管理。该研究区位于97°40'～101°52' E，37°73'～40°06' N，面积约为4.87万km2，多年平均降水量为220～300 mm，多年平均气温为2～6.5 ℃。该地区受中高纬度西风带环流和极地冷空气团的影响，气候干旱，降水稀少且集中[23]。

1.2 数据处理

由于研究区内包含的气象站点有限，因此，本文选用研究区内13个和研究区外7个气象站点的逐月平均降水量、平均气温、最高气温、最低气温、风速、日照时数、水汽压、大气压、相对湿度等气象要素资料，计算20个站点的标准化干旱指数序列，利用反距离权重插值（IDW）方法对所有站点进行空间插值后裁剪得到研究区1961－2014年的干旱指数栅格数据时间序列，用于干旱事件的三维识别，栅格数据的空间分辨率为0.01°×0.01°，时间分辨率为月。其中临泽站气象要素数据序列为1967－2014年，金塔站为1989－2014年，其他站点均为1961－2014年。肃南、临泽、民乐站的数据资料来源于甘肃省气象局，其余站点数据均从中国气象科学数据共享服务网获取（http://data.cma.cn/site/index.html）。研究区概况及站点分布如图1所示。

图1 研究区位置及气象、水文站点分布

2 研究方法

2.1 干旱指标选取

2.1.1 气象干旱指数

本文用标准化降水蒸散指数（SPEI）表征气象干旱。SPEI具有多时间尺度、空间可比性等优点，其计算步骤可参考文献[24]。

1）计算潜在蒸散发（PET，Potential Evapotranspiration），本文利用Penmane-Monteith（PM）方法计算潜在蒸散发，该方法考虑了更多的参数，在物理上更真实，适用于不同地区。计算方法如下：

式中为饱和水汽压温度关系曲线的斜率，kPa/℃；R为到达地面的净辐射量，MJ/(m2·d)；为土壤热通量密度，MJ/(m2·d)；为湿度计常数；为日平均气温，℃；2为地面以上2 m处风速，m/s；e为实际水汽压，kPa；e为空气饱和水汽压，kPa。

2）建立逐月降水量与潜在蒸发量差值序列D，计算公式如下：

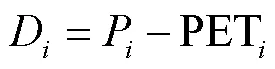
式中为月份；D为月降水量与潜在蒸散量的差值，mm；P为月降水量，mm；PET为月潜在蒸散量，mm。

3）利用log-logistic概率分布函数拟合差值序列并计算概率分布函数()，对()进行标准化处理，即可得到相应SPEI序列：

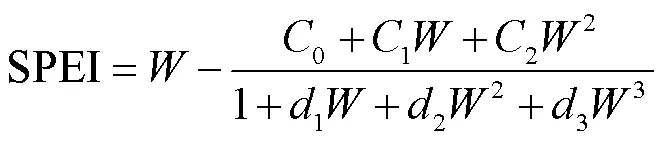
式中当()≤0.5时，()=1−()；当()>0.5时，()=()；其他参数分别为0=2.515 517，1=0.802 853，2=0.010 328，1=1.432 788，2=0.189 269，3=0.001 308。

2.1.2 农业干旱指数

农业干旱通常利用标准化土壤湿度指数或遥感反演的植被指数来表征，而研究区实测的土壤湿度数据序列非常有限，遥感数据的空间分辨率又不能满足精度要求。因此，本文采用Tigkas等提出的农业标准化降水指数（aSPI）来表征农业干旱，通过和其他干旱指数以及实际干旱事件对比发现aSPI在识别农业干旱方面比其他的指数更加稳健[25]。该指数以植物能有效利用的水量作为输入数据，在描述农业干旱特征方面更加完善，并增强了其评估干旱对植被影响的适用性。计算步骤类似于标准化降水指数[26]，其中有效降水量采用适用于干旱半干旱地区的经验公式计算[27-28]：

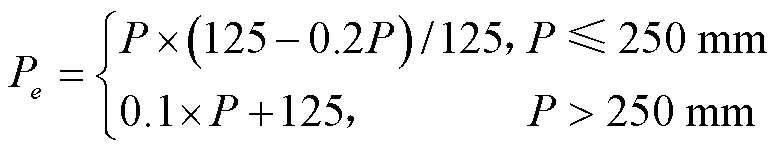
式中P为有效降水量，mm；为降水量，mm。

由于不同时间尺度的标准化干旱指数对干旱事件识别的敏感性不同[11]，短时间尺度对影响因素反映敏感，变化过快，而长时间尺度对其响应减缓，波动过于缓慢[29]，因此，本文选用3个月尺度的标准化干旱指数用于干旱识别。SPEI和aSPI均是经过标准化处理得到的，因此，它们的干旱等级划分均可参考如下标准确定[26]，如表1所示。实际应用中人们更加关注相对严重的干旱事件，为此本文选定-1为干旱阈值。

2.2 干旱事件时空连续三维识别

三维识别方法是从干旱指标的三维空间（时间-经度-纬度）中提取时空连续的干旱事件[30]，主要包括干旱斑块识别和干旱斑块时程连接。

表1 基于标准化干旱指数的干旱等级划分

2.2.1 干旱斑块识别

采用二维干旱识别方法[10]对研究区逐月干旱指数栅格矩阵进行干旱斑块识别，即将干旱指数小于-1的相邻栅格构成一块干旱斑块，并对不同干旱斑块标记不同编号。这一步需要事先设定一个最小干旱面积阈值（），如果某一干旱斑块面积小于，则判定不构成一次干旱事件，将其剔除忽略不计，如图2中3、5。根据该面积阈值也可以判断干旱斑块之间的时间连续性，相关研究[31-33]表明最小干旱面积取值为研究区域的1.6%时较为合理，本文中的取值为779.2 km2（约为750个栅格）。

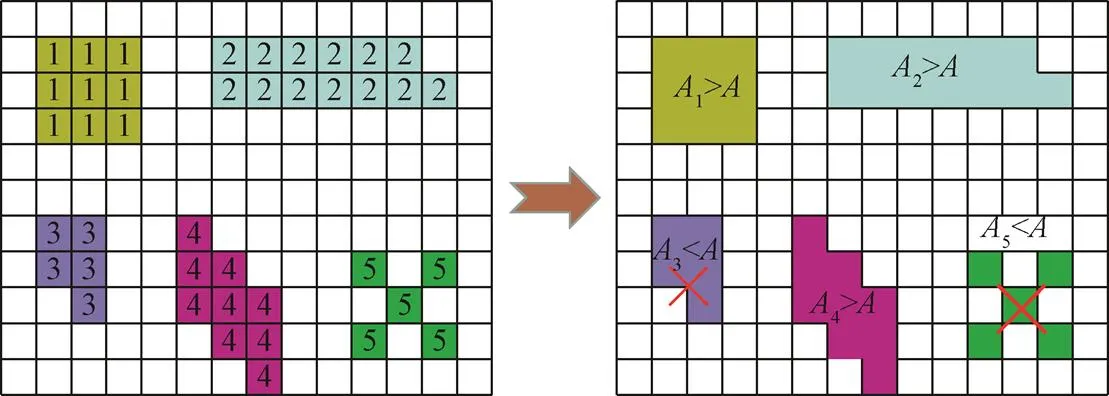
注：A为最小干旱面积阈值；数字为干旱斑块编号。

2.2.2 干旱斑块时程连接

逐月的干旱斑块识别结束后，接着判断时间上干旱斑块之间是否存在联系，从而构成一次干旱事件。假设时刻的某一干旱斑块A和相邻时刻+1的某一干旱斑块A+1之间的重合面积（A）大于阈值，则认为A和A+1在时间上是连续的，判定属于同一场干旱事件，如图3中3和4，反之则不属于同一场干旱事件，如图3中1和2。按照此规则，从第1个月开始依次判断两相邻时刻的任何一对干旱斑块间的重合面积，直到重合面积小于时判定此次干旱事件结束。

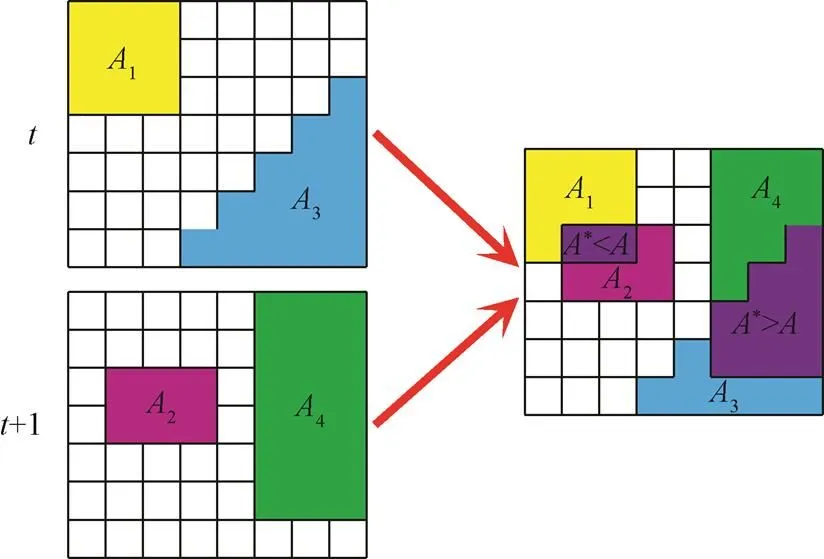
注：时刻t的干旱斑块At和相邻时刻t+1的某一干旱斑块At+1之间的重合面积为A*。

重复上述步骤，将经纬度层面的干旱斑块在时程上连接形成时空连通的干旱指标连续体，获取多场三维干旱事件。

2.2.3 干旱特征变量提取

与二维识别方法相比，基于三维识别方法提取的干旱特征更加复杂，能够更全面地反映干旱时空连续演变特征。本文从干旱历时、面积、烈度、强度、中心点、迁移距离6个干旱特征变量分析单场干旱事件的连续时空演变特征及区域干旱发展规律。

1）干旱历时（，月）：为干旱开始发生至干旱结束所持续的时间长度，三维方法中也可认为是干旱三维空间连续体的高度，如图4所示。

2）干旱面积（，km2）：为干旱三维空间连续体在二维地理坐标平面上的垂直投影面积，如图4所示。

3）干旱烈度（，km2×月）：为所有干旱栅格缺水程度之和，三维识别方法中可认为是干旱三维空间连续体的体积，即为所有干旱栅格体积之和。

4）干旱强度（）：为干旱烈度与干旱历时和干旱面积的比值，表征的是干旱事件发展的严重程度。

5）干旱中心（）：为干旱三维空间连续体的质心，表示一场干旱事件在时间-经度-纬度三维空间中的位置（C、C、C），如图4所示。此外，连续干旱事件每一时刻的干旱斑块也对应一个干旱中心，将他们连接起来可以刻画干旱事件的时空转移路径，了解干旱时空发展规律。

6）干旱迁移距离（）：为干旱事件中相邻两月干旱中心的迁移距离，可以根据相邻两月干旱中心的经纬度坐标换算得到，公式如下：

式中是相邻两月干旱中心的迁移距离，km；Δ和Δ是干旱中心沿经度和纬度方向从月到+1月的迁移距离；X和Y是干旱中心在月的经纬度坐标；X1和Y1是干旱中心在+1月的经纬度坐标。

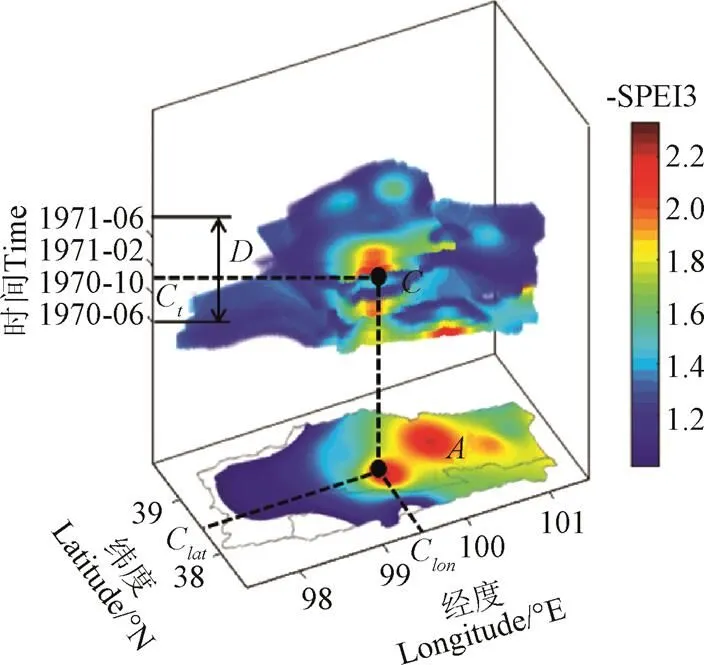
注：C为干旱中心，D为干旱历时。

2.3 气象、农业干旱事件对匹配

基于三维干旱识别结果，从时空尺度对具有对应关系的干旱事件进行匹配，形成干旱事件对，保证匹配结果更符合实际情况。匹配过程及准则如下：

1）对气象、农业干旱事件排序。基于三维干旱识别结果（假设场气象干旱事件，场农业干旱事件），按照时间顺序对气象、农业干旱事件进行排序，构成一个×的矩阵，矩阵中的每个元素（X）代表一对待检测的气象、农业干旱事件。

2）判断待检测的气象、农业干旱事件对是否存在时间上的交集，这是干旱事件对匹配成功的前提。若时间上有交集，在矩阵的对应位置标记为1，否则标记为0。表示为下式：

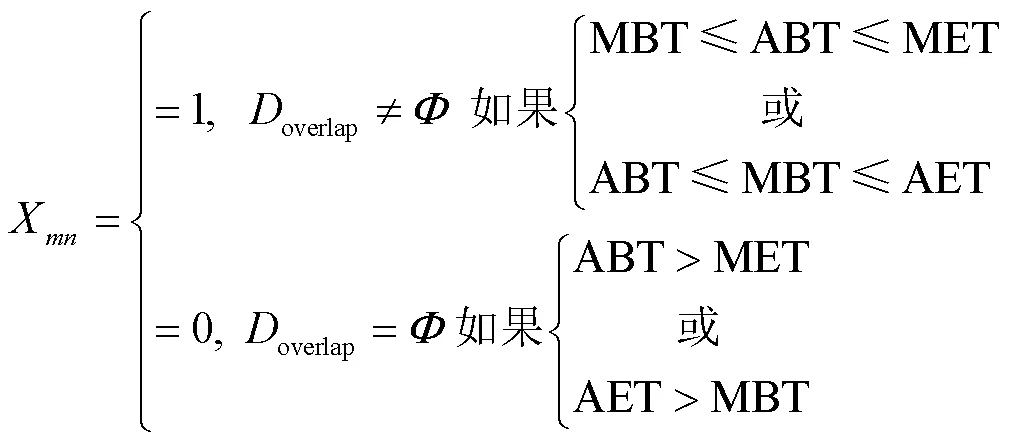
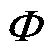
3）对上一步形成的矩阵中标记1位置的气象、农业干旱事件对判断是否存在空间上的交集。通过判断存在时间交集的对应干旱斑块重合面积的大小来判定他们是否属于一次干旱事件对，空间上有交集认为干旱事件对匹配成功，对应位置仍为1，否则修改为0。判别准则如下：

其中Areaoverlap代表干旱斑块面积的交集；AM和AA分别代表气象、农业干旱斑块的干旱面积，km2；为干旱三维识别方法中预先设定的最小干旱面积阈值。

4）对气象、农业干旱事件对进行编码。在第三步形成的矩阵基础上，按照气象、农业干旱事件编号顺序对匹配成功的干旱事件对进行编码，如果存在同一场气象干旱引发多场农业干旱或多场气象干旱引起同一场农业干旱，则对应位置标记相同的编码，如图5所示。

气象、农业干旱事件对匹配成功并编码后，需对同干旱类型中不同干旱事件在时空尺度上进行整合处理，并计算气象、农业干旱特征，用于3.2.3节建立气象-农业干旱特征响应关系。整合后新生成的气象（农业）干旱历时定义为第一场干旱事件开始至最后一场干旱事件结束的经历时间长度；干旱烈度为所有干旱事件干旱烈度值的总和；干旱面积为每一时刻干旱事件的干旱面积在经纬度平面上的投影并集。

图5 气象、农业干旱事件匹配成功后干旱事件对编码示意图

3 结果与分析

3.1 干旱时空动态演变特征

首先，基于三维干旱识别方法详细分析单场气象、农业干旱事件的连续动态演变过程，然后基于识别结果探讨气象、农业干旱的响应特征，可为抗旱减灾及水资源管理提供理论依据，同时为研究干旱传递机制提供新思路。

基于SPEI-3和aSPI-3，利用干旱三维识别方法在黑河流域中上游1961－2014年共识别出170场气象干旱和198场农业干旱，表2列出了最严重的5场气象、农业干旱事件。如表2所示，除第19场农业干旱事件外，其余所有干旱事件的干旱面积均占整个研究区的90%以上。其中，最严重的气象干旱发生在1970年6月至1971年8月，历时15个月，最严重的农业干旱发生在1962年1月至1962年9月，历时9个月。分别以最严重的气象干旱（No.25）和农业干旱（No.1）为例，详细分析单场干旱事件时空连续的动态演变过程。

表2 1961－2014年严重的气象、农业干旱事件的干旱特征

如图6所示，第25场气象干旱于1970年6月起源于临泽县境内，干旱面积仅843.14 km2，干旱烈度为937 月·km2；同年7月干旱迅速向整个研究区蔓延，旱情最为严重，干旱面积达到4.24万km2，约占研究区面积的87%，干旱中心位于肃南县的中部；1970年8月至9月，干旱强度有所下降，干旱面积有所减小并向中部集中，且干旱中心向西北方向迁移13.86 km至高台县境内；随后两个月干旱面积持续减小，主要集中在高台县、临泽县和祁连县的部分区域；之后旱情并没有得到缓解，而是进一步向研究区东部扩张，1970年12月至1971年3月为本场干旱事件的第二个高峰期，干旱面积占研究区面积的54%～71%，平均干旱烈度为4.37×104月·km2，干旱中心均集中在肃南县境内靠近张掖市附近；1971年4月至7月，旱情衰减，干旱面积呈带状由东北-西南方向穿越研究区，干旱中心又迁移至肃南县中部；1971年8月，旱情迅速减弱，干旱面积仅有0.12万km2，干旱中心向东南方向迁移94.96 km至祁连县东部，并最终在此消亡。综上所述，本场气象干旱共历时15个月，旱情经历了发生-强化-衰减-再强化-再衰减-消亡6个过程，干旱中心迁移路径大致为临泽县→肃南县中部→高台县→肃南县东部→肃南县中部→祁连县。

如图7所示，1962年的农业干旱大致也经历了发生-强化-衰减-再强化-再衰减-消亡6个过程。该场干旱发生于1962年1月，干旱面积为0.29万km2，干旱烈度为3414.4 月·km2；2月干旱面积扩大至3.14万km2，占研究区面积的64.5%，干旱中心迁移至肃南县中部；3－4月旱情有所减缓，平均干旱面积为1.96万km2，中心向东南方向迁移20.61 km至肃南县东南部；5－7月为本场干旱的又一个高峰期，其中6月旱情最为严重，干旱面积覆盖整个研究区，干旱烈度为1×105月·km2，干旱中心均集中在肃南县中部；8月旱情有所减缓，干旱面积缩小至3.44万km2；9月旱情迅速衰减，干旱中心转移至山丹县并在此消亡。

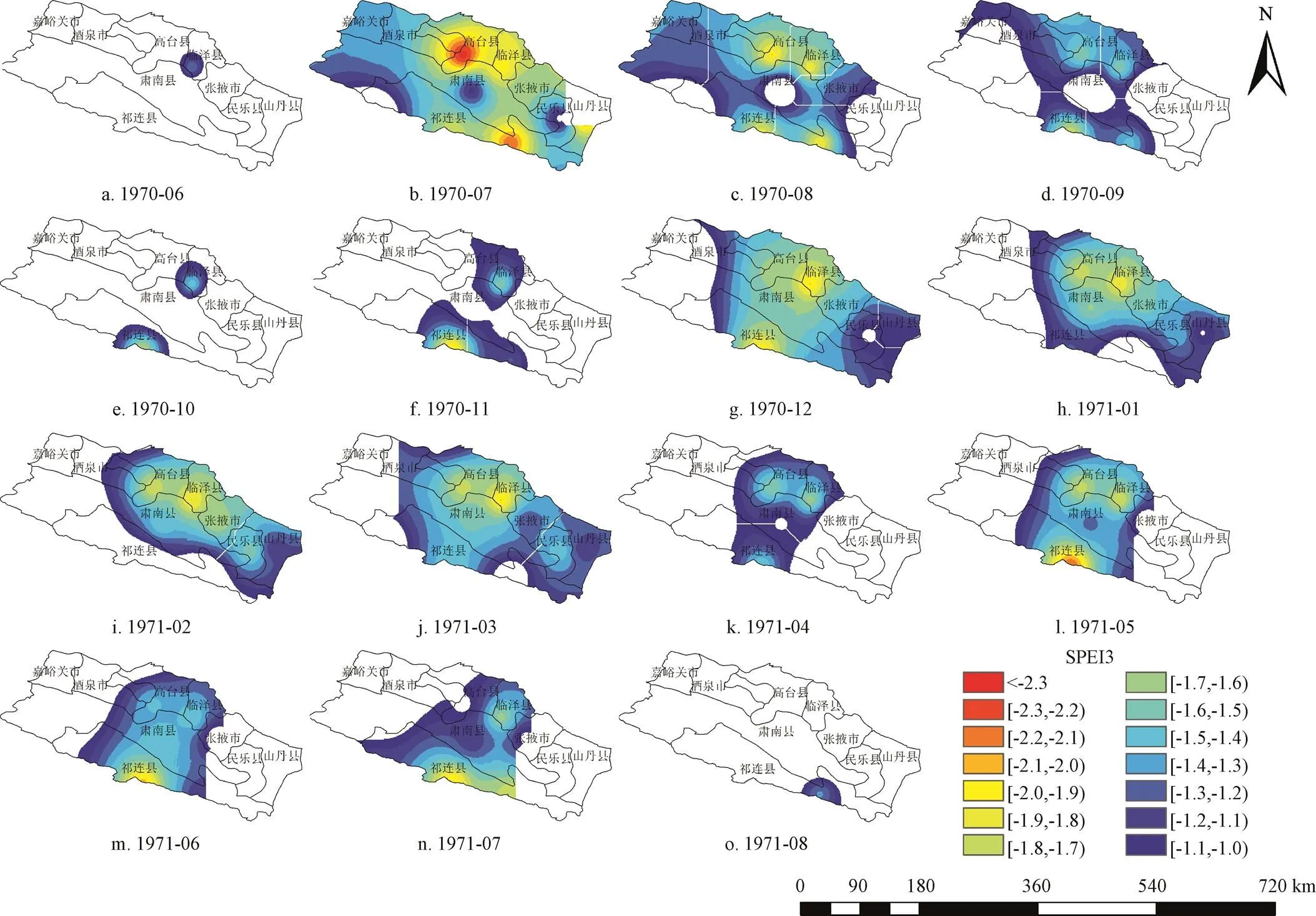
图6 1970－1971年气象干旱时空动态演变图

图7 1962年农业干旱时空动态演变图

通过分析不同季节连旱年的气象干旱发展规律可知，研究区秋冬春3季连旱年的气象干旱事件发展规律较为明显。因此，本文选取研究时段内秋冬春3季连旱年，即1972－1973、1974－1975、1980－1981和2013－2014年的气象干旱事件，根据各场干旱事件中心的迁移路径总结研究区秋冬春连旱事件的整体迁移规律，大体上为：秋冬春连旱一般起源于中游中部，然后沿东南方向逐渐向上游迁移，最后终止于上游；干旱迁移路径大致呈西北-东南方向的喇叭口状，且干旱在上游区域的迁移速率相对较快，如图8所示。气象干旱呈现出这种迁移规律是气候条件的地域差异造成的，黑河流域气候具有明显的东西差异和南北差异，降水量由东向西递减，蒸发量则由东向西递增，且蒸发量远远大于降水量；而由北向南海拔逐渐增高，随着海拔的增高，降水量增加，蒸发量减小。

图8　1961－2014年秋冬春连旱年气象干旱发展规律

3.2 气象、农业干旱响应关系

3.2.1 基于时空尺度的气象-农业干旱事件对匹配

根据时空尺度干旱事件对匹配准则，1962－2014年研究区内共成功匹配干旱事件对58场，如图9所示。图中颜色相同的位置表示对应位置上的气象、农业干旱事件属于同一场干旱事件对，椭圆表示对应位置上的气象、农业干旱事件匹配失败。从图中可以看出，匹配成功的干旱事件对沿对角线均匀分布，表明匹配之前的气象、农业干旱事件在时间上具有较高的一致性。同时，图中出现较多的沿横轴持续的条带，表明基于三维视角的气象-农业干旱对应关系中，经常发生一场气象干旱引发多场农业干旱的状况。

图9 时空尺度气象、农业干旱事件对匹配结果

匹配前后气象、农业干旱历时、烈度、面积3个干旱特征分布状况如图10所示。可以看出，在三维气象-农业干旱的对应关系中，大多匹配失败的干旱事件是一些历时较短、烈度较小、影响面积较小的小干旱事件。由于存在多场气象干旱对应多场农业干旱的状况，匹配成功的气象、农业干旱事件对需要进行合并，匹配成功前后气象、农业干旱特征发生显著变化，匹配成功合并后的干旱事件具有历时延长、烈度增强、面积增加的显著特征。

图10 匹配前后气象、农业干旱特征分布图

3.2.2 气象-农业干旱事件时空响应特征

气象、农业干旱之间的响应关系主要包括一场气象干旱引发一场农业干旱、一场气象干旱引发多场农业干旱、多场气象干旱引发一场农业干旱。第一种响应关系相对容易理解，因此，本文以第二、三种响应关系为例来讨论气象-农业干旱事件复杂的时空响应特征。根据2.2.2节的干旱斑块时程连接准则判别后发现图11中的4场农业干旱以及图12中的3场气象干旱对应干旱斑块的重合面积小于预先设定的最小干旱面积阈值，即它们并不属于一次连续的干旱事件。

以匹配成功的No.57干旱事件对为例，分析No.166场气象干旱（2012-10－2013-06）与引发的4场农业干旱之间的时空响应特征，如图11所示。图中所示为气象、农业干旱事件在特定时段内累积干旱指数在经纬度坐标平面的投影。该次气象-农业干旱时空响应特征分为2个阶段：第一个阶段（图11a）为2012年10月至2013年2月，No.166场气象干旱处于发展阶段，诱发了No.192场农业干旱（2012-10），且两者在空间分布上具有较高的一致性，干旱面积均集中在研究区西部，旱情较严重区域均位于祁连县的西部。第二阶段（图11b）为2013年3月至6月，No.166场气象干旱持续扩张，干旱面积覆盖整个研究区，并相继引发了覆盖研究区80%以上的No.193场（2013-03－2013-05）、位于肃南县西南角的No.194场（2013-04）和覆盖嘉峪关市、酒泉西部以及肃南县西北角的No.195场（2013-05）3场农业干旱，且旱情的空间分布具有较好的一致性。

以匹配成功的No.40干旱事件对为例，分析No.154场农业干旱（2001-02－2001-08）与其有关的3场气象干旱之间的时空响应特征，如图12所示。该次气象-农业干旱事件对时空响应特征主要表现为：2001年2月至8月发生在研究区西部的No.118场气象干旱、2001年6月至8月发生在研究区东部的No.120场气象干旱以及2001年8月发生在高台县和临泽县交接处的No.121场气象干旱共同引发了覆盖整个研究区的No.154场农业干旱。

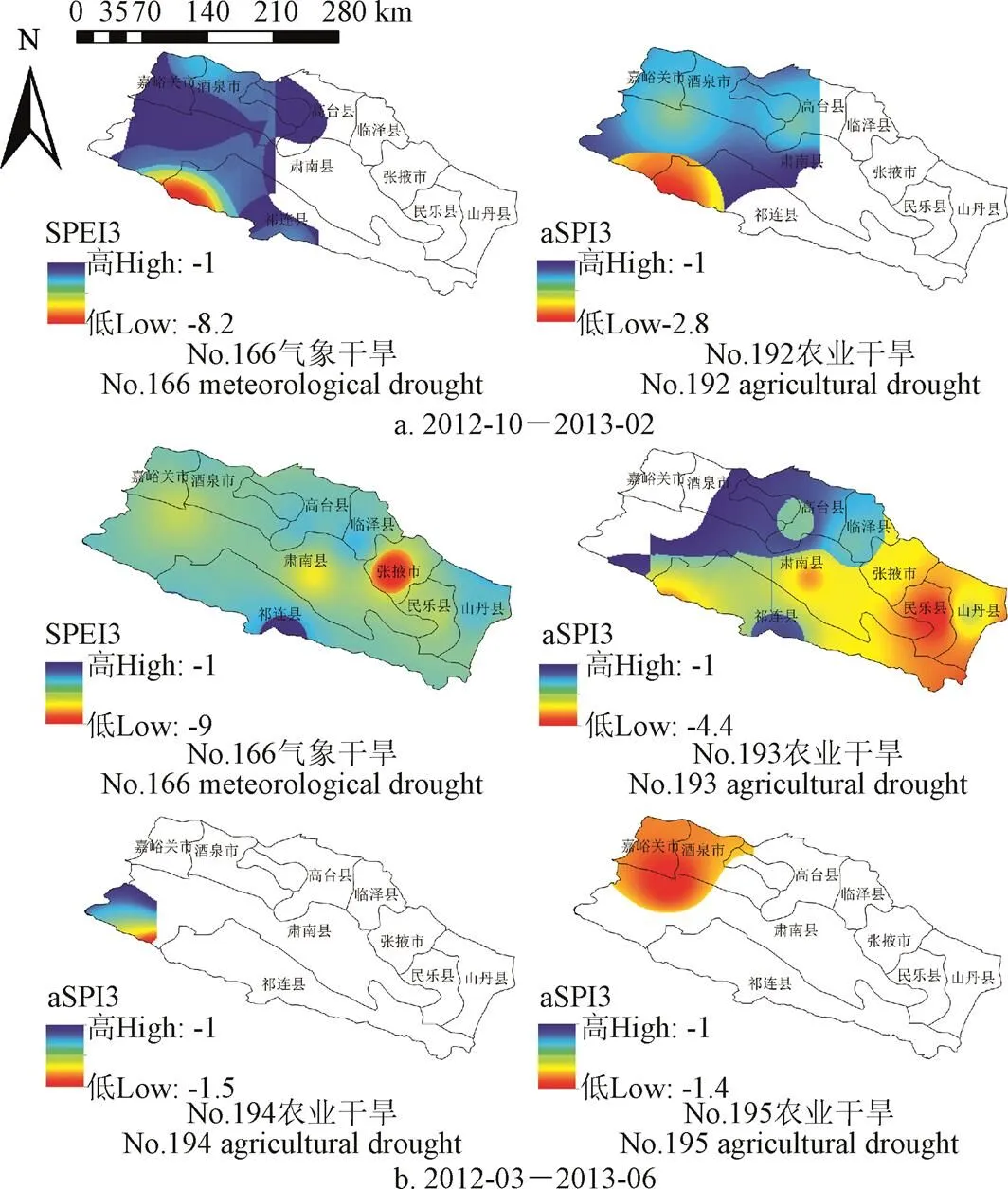
图11 四场农业干旱对No.166场气象干旱的时空响应特征

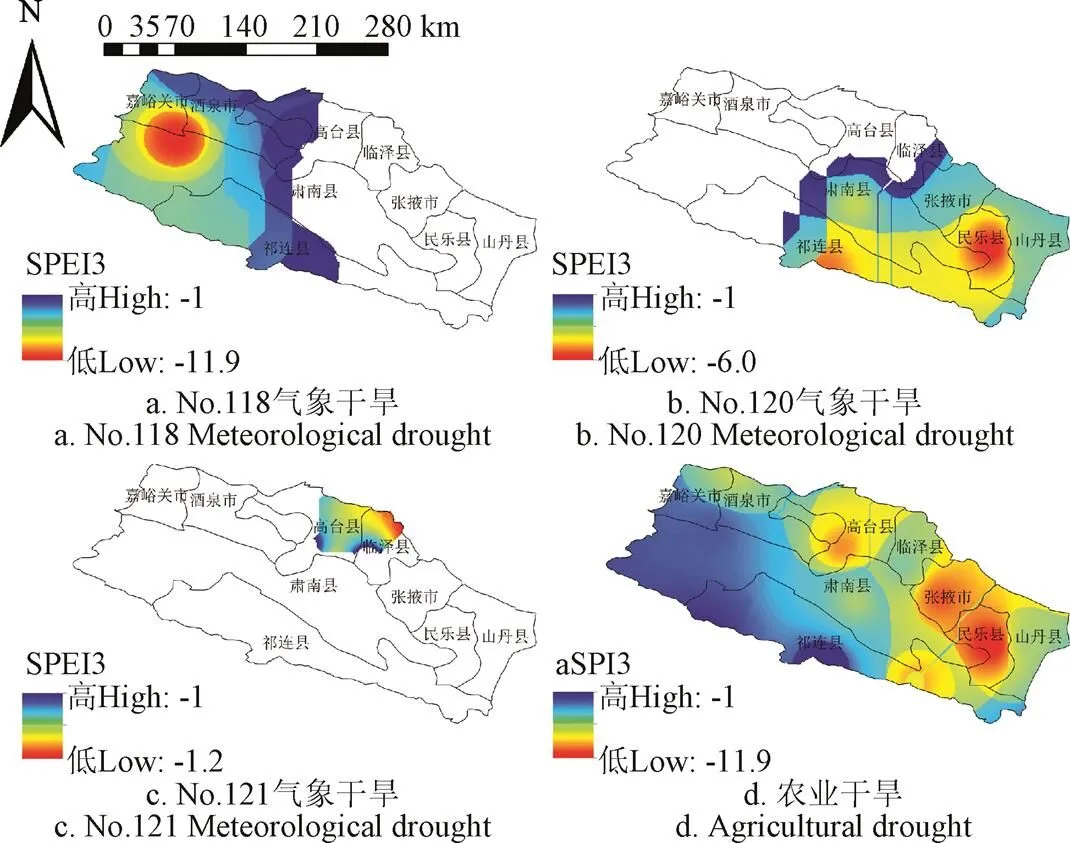
图12 No.154场农业干旱对三场气象干旱的时空响应特征

将匹配成功的干旱事件对所对应的气象、农业干旱中心进行投影，得到气象、农业干旱事件中心的空间分布格局，如图13所示。由图13可知，气象、农业干旱事件的中心位置及旱情严重程度在空间上具有较高的一致性，干旱中心主要集中在嘉峪关，酒泉及肃南交界处、肃南中部、民乐、山丹以及祁连县部分区域。旱情严重区域沿中游呈西北-东南方向带状分布，主要集中在嘉峪关、酒泉、肃南、高台、张掖、民乐以及山丹县，与干旱中心的主要分布区域基本吻合。

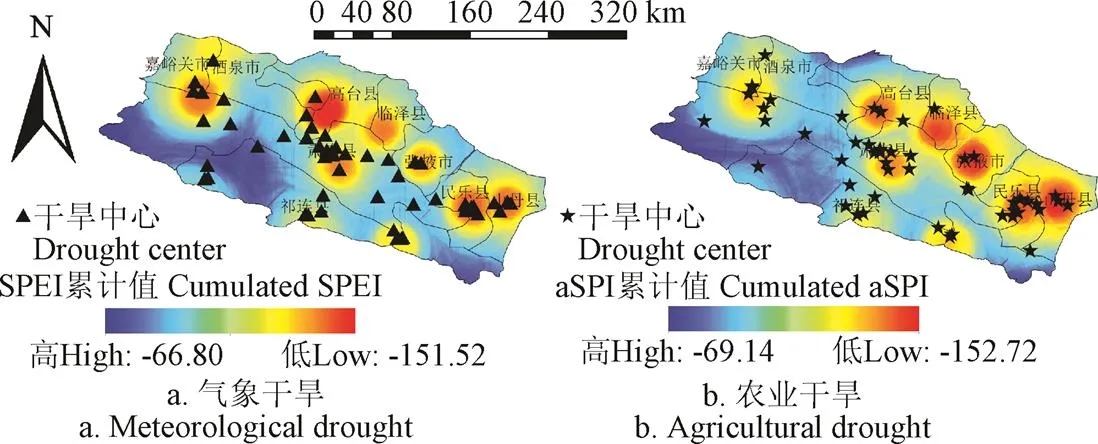
图13 匹配成功的气象、农业干旱中心空间分布

3.2.3 气象-农业干旱特征响应关系

采用交叉验证方法[34]，将匹配成功的58场干旱事件对分为3组样本分别构建不同干旱特征的4种响应关系模型，根据验证结果确定干旱特征的最优响应关系模型。第一组为第1-38场干旱事件对构建响应关系模型，剩余第39-58场干旱事件对来验证模型；第二组为第7-44场干旱事件对构建响应关系模型，剩余第1-6和第45-58场干旱事件对来验证模型；第三组为第21-58场干旱事件对构建响应关系模型，剩余第1-20场干旱事件对来验证模型，响应关系模型及验证结果见表3。

由表3可知，干旱历时响应关系模型中，最大相关系数为0.89，最小为0.62；干旱面积响应关系模型中，最大相关系数为0.70，最小为0.55；干旱面积响应关系模型中，最大相关系数为0.75，最小为0.50；所有结果均通过=0.05显著性检验，可见研究区农业干旱对气象干旱具有密切的响应关系。由表3的验证结果可知，干旱特征响应模型均是在第二组中验证结果最优，且干旱历时最优响应模型为=1.45+0.25+0.042，干旱面积最优响应模型为=exp(−0.81+0.49−0.012)，干旱烈度最优响应模型为=exp(−2.47+1.94−0.272)。

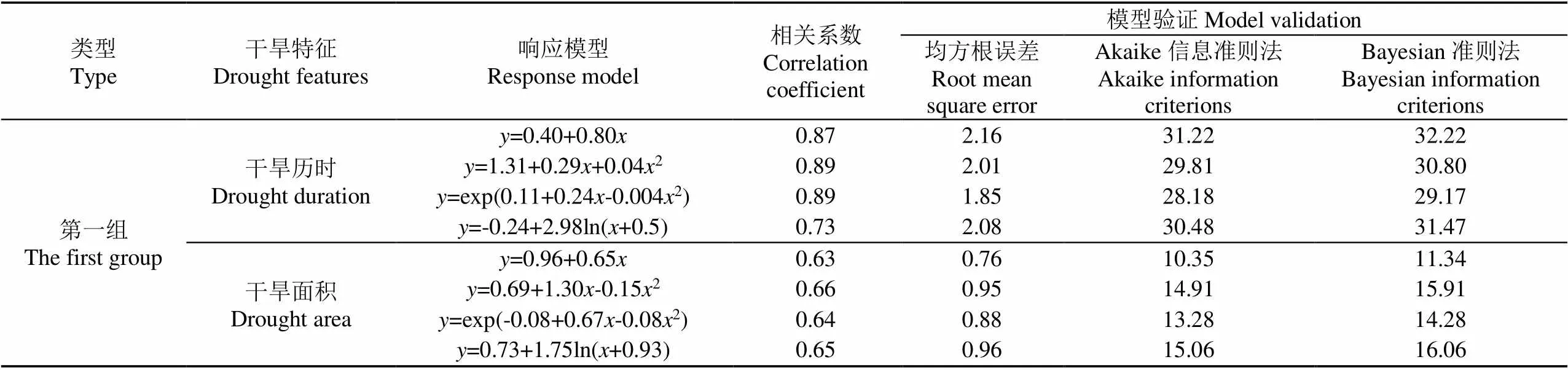
表3 气象-农业干旱特征响应模型及验证结果

续表

注：-农业干旱特征；-气象干旱特征；所有拟合结果均通过=0.05显著性检验。

Note:-Agriculture drought variables；-Meteorological drought variables；all the results pass the significance test at=0.05。

4 结 论

本文利用三维干旱识别方法提取时空连续的干旱事件，基于时空尺度匹配相关联的干旱事件对，通过干旱时空特征变量研究1961－2014年黑河流域气象、农业干旱事件时空动态演变规律及时空响应特征。主要结论如下：

1）基于三维视角能够全面准确地刻画干旱事件时空连续的动态演变过程，为定量研究干旱变化提供参考；且黑河流域秋冬春连旱的发展规律为起源于中游中部，沿东南方向逐渐向上游迁移，最后终止于上游，且上游区域干旱的迁移速率相对较快；

2）基于时空尺度的干旱事件对匹配结果发现干旱事件之间的联系比较复杂，如一场气象干旱引发不同位置的农业干旱或多场气象干旱引发一场农业干旱，且旱情轻微的气象干旱不容易引发农业干旱，旱情严重的气象干旱经常引发时空格局复杂的农业干旱，同时，该时空匹配准则为定量研究不同类型干旱间的响应特征提供新思路；

3）基于干旱事件对匹配结果建立了农业干旱特征对气象干旱特征的响应关系，干旱历时最优响应模型为二次多项式，干旱面积和干旱烈度的最优响应模型均为指数函数。

本研究结果对从时空尺度理解干旱传递机制有重要意义，但本文只是构建了气象、农业干旱间的响应函数模型，进一步研究可以考虑构建气象、农业干旱间的传递概率模型，并根据响应函数模型及概率传递模型进行定量的干旱预测，比较它们之间的优劣，可为更好的了解干旱机制提供理论依据。

[1] Leng G, Tang Q, Rayburg S. Climate change impacts on meteorological, agricultural and hydrological droughts in China[J]. Global and Planetary Change, 2015, 126: 23－34.

[2] Deo R C, Byun H-R, Adamowski J F, et al. Application of effective drought index for quantification of meteorological drought events: A case study in Australia[J]. Theoretical and Applied Climatology, 2016, 128(1/2): 359－379.

[3] Deng S, Chen T, Yang N, et al. Spatial and temporal distribution of rainfall and drought characteristics across the Pearl River basin[J]. Science of the Total Environment, 2018, 619－620: 28-41.

[4] 李敏，李建柱，冯平，等. 变化环境下时变标准化径流指数的构建与应用[J]. 水利学报，2018，49(11)：1386-1395.

Li Min, Li Jianzhu, Feng Ping, et al. Construction of time-dependent drought index under changing environment and its application[J]. Journal of Hydraulic Engineering, 2018, 49(11): 1386-1395. (in Chinese with English abstract)

[5] Lesk C, Rowhani P, Ramankutty N. Influence of extreme weather disasters on global crop production[J]. Nature & Insects, 2016, 529(7584): 84-87.

[6] 詹存，梁川，赵璐. 川中丘陵区季节性干旱时空分布特征及成因分析[J]. 农业工程学报，2013，29(21)：82-90.

Zhan Cun, Liang Chuan, Zhao Lu. Temporal and spatial distribution characteristics and causes analysis of seasonal drought in hilly area of central Sichuan[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2013, 29(21): 82-90. (in Chinese with English abstract)

[7] 李斌，解建仓，胡彦华，等. 基于标准化降水指数的陕西省干旱时空变化特征分析[J]. 农业工程学报，2017，33(17)：113-119.

Li Bin, Xie Jiancang, Hu Yanhua, et al. Analysis on spatiotemporal variability characteristics of drought in Shaanxi Province using standardized precipitation index[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2017, 33(17): 113-119. (in Chinese with English abstract)

[8] Corzo Perez G A, Van Huijgevoort M H J, Voss F, et al. On the spatio-temporal analysis of hydrological droughts from global hydrological models[J]. Hydrology and Earth System Sciences Discussions, 2011, 15(9): 2963-2978.

[9] Zhai J Q, Huang J L, Su B D, et al. Intensity-area-duration analysis of droughts in China 1960－2013[J]. Climate Dynamics, 2017, 48(1/2): 151-168.

[10] Andreadis K M, Clark E A, Wood A W, et al. Twentieth-century drought in the conterminous United States[J]. Journal of Hydrometeorology, 2005, 6(6): 985-1001.

[11] 方国华，涂玉虹，闻昕，等. 1961－2015年淮河流域气象干旱发展过程和演变特征研究[J]. 水利学报，2019，50(5)：598-611.

Fang Guohua, Tu Yuhong, Wen Xin, et al. Study on the development process and evolution characteristics of meteorological drought in the Huaihe River Basin from 1961 to 2015[J]. Journal of Hydraulic Engineering, 2019, 50(5): 598-611. (in Chinese with English abstract)

[12] Mishra A K, Singh V P. A review of drought concepts[J]. Journal of Hydrology, 2010, 391(1/2): 202-216.

[13] 裴源生，蒋桂芹，翟家齐. 干旱演变驱动机制理论框架及其关键问题[J]. 水科学进展，2013，24(3)：449-456.

Pei Yuansheng, Jiang Guiqin, Zhai Jiaqi. Theoretical framework of drought evolution driving mechanism and the key problems[J]. Advances in Water Science, 2013, 24(3): 449-456. (in Chinese with English abstract)

[14] 李运刚，何娇楠，李雪. 基于SPEI和SDI指数的云南红河流域气象水文干旱演变分析[J]. 地理科学进展，2016，35(6)：758-767.

Li Yungang, He Jiaonan, Li Xue, et al. Hydrological and meteorological droughts in the Red River Basin of Yunnan Province based on SPEI and SDI indices[J]. Progress in Geography, 2016, 35(6): 758-767. (in Chinese with English abstract)

[15] 胡彩虹，赵留香，王艺璇，等. 气象、农业和水文干旱之间关联性分析[J]. 气象与环境科学，2016，39(4)：1-6.

Hu Caihong, Zhao Liuxiang, Wang Yixuan, et al. Analysis of the relationship between the meteorological, agriculture and hydrological drought[J]. Meteorological and Environmental Sciences, 2016, 39(4): 1-6. (in Chinese with English abstract)

[16] 张建龙，王龙，杨蕊，等. 南盘江流域水文干旱对气象干旱的响应特征[J]. 南水北调与水利科技，2014，12(3)：29-32.

Zhang Jianlong, Wang Long, Yang Rui, et al. Response characteristics of hydrological droughts to climatic droughts in Nanpan River Basin[J]. South-to-North Water Transfers and Water Science & Technology, 2014, 12(3): 29-32. (in Chinese with English abstract)

[17] Huang S, Li P, Huang Q, et al. The propagation from meteorological to hydrological drought and its potential influence factors[J]. Journal of Hydrology, 2017, 547: 184-195.

[18] Ye X C, Li X H, Xu C Y, et al. Similarity, difference and correlation of meteorological and hydrological drought indices in a humid climate region - the Poyang Lake catchment in China[J]. Hydrology Research, 2016, 47(6): 1211-1223.

[19] Huang S, Huang Q, Chang J, et al. The response of agricultural drought to meteorological drought and the influencing factors: A case study in the Wei River Basin, China[J]. Agricultural Water Management, 2015, 159: 45-54.

[20] 吴杰峰，陈兴伟，高路. 水文干旱对气象干旱的响应及其临界条件[J]. 灾害学，2017，32(1)：199-204.

Wu Jiefeng, Chen Xingwei, Gao Lu. Response of hydrological drought to meteorological drought and its critical conditions[J]. Journal of Catastrophology, 2017, 32(1): 199-204. (in Chinese with English abstract)

[21] Zhu Y, Liu Y, Wang W, et al. Three-dimensional characterization of meteorological and hydrological droughts and their probabilistic links[J]. Journal of Hydrology, 2019, 578: 124016.

[22] 艾启阳，粟晓玲，张更喜，等. 标准化地下水指数法分析黑河中游地下水时空演变规律[J]. 农业工程学报，2019，35(10)：69-74.

Ai Qiyang, Su Xiaoling, Zhang Gengxi, et al. Constructing standardized groundwater index to analyze temporal-spatial evolution of groundwater in middle reaches of Heihe river[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2019, 35(10): 69-74. (in Chinese with English abstract)

[23] 钟锋，粟晓玲，郭静. 黑河流域干旱指数的变化趋势及其多时间尺度特征[J]. 西北农林科技大学学报：自然科学版，2017，45(9)：136-144.

Zhong Feng, Su Xiaoling, Guo Jing. Trends and multiple time scale characteristics of aridity index in Heihe river basin[J]. Journal of Northwest A&F University: Natural Science Edition, 2017, 45(9): 136-144. (in Chinese with English abstract)

[24] 沈国强，郑海峰，雷振锋. 基于SPEI指数的1961－2014年东北地区气象干旱时空特征研究[J]. 生态学报，2017，37(17)：5882-5893.

Shen Guoqiang, Zheng Haifeng, Lei Zhenfeng. Spatiotemporal analysis of meteorological drought (1961－2014) in Northeast China using a standardized precipitation evapotranspiration index[J]. Acta Ecologica Sinica, 2017, 37(17): 5882-5893. (in Chinese with English abstract)

[25] Tigkas D, Vangelis H, Tsakiris G. Drought characterisation based on an agriculture-oriented standardised precipitation index[J]. Theoretical and Applied Climatology, 2018, 135(3/4): 1435-1447.

[26] 黄晚华，杨晓光，李茂松，等. 基于标准化降水指数的中国南方季节性干旱近58 a演变特征[J]. 农业工程学报，2010，26(7)：50-59.

Huang Wanhua, Yang Xiaoguang, Li Maosong, et al. Evolution characteristics of seasonal drought in the south of China during the past 58 years based on standardized precipitation index[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2010, 26(7): 50-59. (in Chinese with English abstract)

[27] Smith M. CROPWAT-a computer program for irrigation planning and management[R]. FAO Irrigation and Drainage. Rome, Italy, 1992.

[28] Kourgialas N N, Karatzas G P, Morianou G. Water management plan for olive orchards in a semi-mountainous area of Crete, Greece[J]. Glob Nest Journal, 2015, 17(1): 72-81.

[29] 王飞，王宗敏，杨海波，等. 基于SPEI的黄河流域干旱时空格局研究[J]. 中国科学：地球科学，2018，48(9)：1169-1183.

Wang Fei, Wang Zongmin, Yang Haibo, et al. Study of the temporal and spatial patterns of drought in the Yellow River basin based on SPEI[J]. Scientia Sinica (Terrae), 2018, 48(9): 1169-1183. (in Chinese with English abstract)

[30] 徐翔宇，许凯，杨大文，等. 多变量干旱事件识别与频率计算方法[J]. 水科学进展，2019，30(3)：373-381.

Xu Xiangyu, Xu Kai, Yang Dawen, et al. Drought identification and drought frequency analysis based on multiple variables[J]. Advances in Water Science, 2019, 30(3): 373-381. (in Chinese with English abstract)

[31] Wang A H, Lettenmaier D P, Sheffield J. Soil moisture drought in China, 1950-2006[J]. Journal of Climate, 2011, 24(13): 3257-3271.

[32] Xu K, Yang D W, Yang H B, et al. Spatio-temporal variation of drought in China during 1961－2012: A climatic perspective[J]. Journal of Hydrology, 2015, 526: 253-264.

[33] Liu Y, Zhu Y, Ren L, et al. Understanding the spatiotemporal links between meteorological and Hydrological droughts from a three-dimensional perspective[J]. Journal of Geophysical Research: Atmospheres, 2019, 124(6): 3090-3109.

[34] Shao J. An asymptotic theory for linear model selection[J]. Statistica Sinica, 1997, 7(2): 221-242.

Spatiotemporal response characteristics of agricultural drought to meteorological drought from a three-dimensional perspective

Feng Kai, Su Xiaoling※

(1.,712100; 2.&712100)

Meteorological drought is an important driving factor of agriculture drought in their inherent correlation. Characteristics and estimation of agricultural drought response to meteorological drought can contribute to understanding the mechanism of drought evolution, and assessment of drought mitigation measures. However, most previous studies are lacking in the spatiotemporal continuity of drought evolution. In this study, the spatiotemporal dynamic evolution of droughts in the Heihe River Basin during 1961-2014 was analyzed using a three-dimensional identification method, where the standardized precipitation evapotranspiration index (SPEI) and agriculture standardized precipitation index (aSPI) were used to evaluate the meteorological drought and agricultural drought. A spatiotemporal matching criterion of drought event was proposed to determine the event pair of meteorological-agricultural drought, and thereby a response model of drought variables was established based on the spatiotemporal characteristics of agriculture drought response to meteorological drought. The results showed that 1) three-dimensional perspective can benefit to recognition for the dynamic evolution rules of drought events. Six drought variables were selected as indicators, including drought duration, area, severity, intensity, center and migration trajectory, to analyze the drought evolution for Heihe River basin in 1961-2014. Specifically, the most severe meteorological drought event (No.25) originated in Linze county in June 1970, showing the drought-affected area of only 843.14 km2. The drought spread rapidly to the whole study area in July, with the drought-affected area of 42 400 km2, accounting for about 87% of the study area, and the drought center is located in the middle of Sunan county. The subsequent drought moved approximately 13.86 km in the northwest direction from August to September 1970 with the decrease of drought intensity and affected area. In the next two months, the drought areas continuously decreased, and mainly concentrated in Gaotai, Linze and Qilian county. The second peak of this drought occurred from December 1970 to March 1971, the drought-affected areas accounting for 54%-71% of the study area, with the drought severity of 43 700 km2·month. The drought center moved 94.96 km toward southeast to eastern Qilian county, and finally diminished there from April to July 1971. The continuous droughts in autumn, winter and spring generally originated from the middle-stream, and gradually migrated to the upstream along the southeast direction, particularly that the rate of drought migration was relatively high in the upstream. 2) The matching results of drought events based on spatiotemporal scale can ensure that the complex relationship between meteorological and agricultural drought well agrees with the practical situation, with the high accuracy of response analysis. The drought events after successful matching demonstrate the specific characteristics, including prolonged duration, enhanced intensity and increase affected area. 3) The optimal response models of drought duration, area and severity between meteorological and agricultural drought follow the quadratic polynomial, the exponential function and exponential function, respectively. This finding can provide an insightful understanding to accurate evaluate the spatiotemporal dynamic evolution and the response relationship of droughts.

drought; meteorology; agriculture; dynamic evolution; drought matching

冯凯，粟晓玲. 基于三维视角的农业干旱对气象干旱的时空响应关系[J]. 农业工程学报，2020，36(8)：103-113.doi：10.11975/j.issn.1002-6819.2020.08.013 http://www.tcsae.org

Feng Kai, Su Xiaoling. Spatiotemporal response characteristics of agricultural drought to meteorological drought from a three-dimensional perspective[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2020, 36(8): 103-113. (in Chinese with English abstract) doi：10.11975/j.issn.1002-6819.2020.08.013 http://www.tcsae.org

2019-12-10

2020-02-12

国家自然科学基金资助项目（51879222）

冯凯，博士生，主要从事干旱演变及响应方面研究。Email：fengk0121@163.com

粟晓玲，教授，博士生导师，主要从事水文模拟及水资源优化方面的研究。Email：xiaolingsu@nwafu.edu.cn

10.11975/j.issn.1002-6819.2020.08.013

P429

A

1002-6819(2020)-08-0103-11