不同编制型式钢制系缆的动力响应

张若瑜，赵凤帅，林风梅，郄亚克，李 焱

不同编制型式钢制系缆的动力响应

张若瑜1, 2，赵凤帅1, 2，林风梅3，郄亚克3，李 焱1, 2

(1. 天津大学建筑工程学院，天津 300072；2. 天津大学天津市港口与海洋工程重点实验室，天津 300072；3. 巨力索具股份有限公司，保定 072550)

针对国内研究易忽视的钢缆扭转特性，建立了不同编制型式钢缆的拉伸-扭转模型. 首先，分析钢缆结构特性、钢丝材料性质等基本特征，明确其在海洋工程中的受力状态，并基于合理假设，将钢缆应力分布问题简化为几何问题，确定拉伸-扭转共同作用下的钢缆本构关系. 在此基础上，针对钢丝之间的不同接触特点，将赫兹接触理论推广到钢缆的数值模拟中，建立点接触和线接触的接触应力求解方法. 其次，基于非线性动力学理论，考虑外载荷作用，并在钢缆刚度中引入拉伸-弯曲-扭转耦合项，推导钢缆动力学平衡方程组. 在此基础上，建立了系泊系统计算模型，得出外载荷作用下的钢缆动力响应，并分析了在轴向载荷作用下，钢缆的扭转特性对张力的影响. 此外，还研究了不同编制型式钢缆的扭转作用对缆绳动内力的影响，得出张力变化规律. 结果表明：在相同轴向载荷下，不同编制型式钢缆的动力响应不同；不同的编制型式会影响张力数值，与忽略扭转特性时得出的张力相比，考虑钢缆结构扭转特性时计算出的张力增大，并且增大的数值受编制型式影响；不同编制型式会导致截面应力分布不均匀，钢缆内部应力分布与其编制型式密切相关，因此，在对钢缆进行应力计算，特别是接触应力分析时，考虑其具体编制型式极为必要，6×19型钢缆由于自身钢丝左捻右捻的交互排列型式，受到外载荷时的响应较低.

钢制系缆；动力响应；拉伸-扭转特性；编制型式

钢缆在使用过程中，会受到轴向载荷作用，由于钢缆自身螺旋编制的结构特点，会发生扭转作用. 在周期性载荷作用下，相连的纤维缆和钢缆会在连接处产生一定的旋转角度，这种循环作用会造成钢缆的疲劳破坏．这种疲劳形式，被称为拉伸-扭转疲劳．有研究显示，钢缆受到拉伸-扭转耦合作用比单纯受到拉伸作用时耐久度会损失95%[1]．不同编制型式的钢缆由于自身的复杂结构，具有不同的扭转性能．为预防钢缆的拉伸-扭转疲劳破坏，得出扭转特性对钢缆性能的影响，对不同编制型式的钢缆进行力学分析十分必要.

目前，国内外学者针对系缆结构进行了分析. Kim等[2]基于拉格朗日方程，设计了一种用于缆索非线性分析的等参曲线索单元，并利用罚函数与载荷增量法给出了确定系统平衡状态的方法，同时将Newmark方法应用于系缆的动力分析．Zhu等[3]开发了一种曲线弹性梁单元，用于解决海洋低张力系缆的问题，但这种梁单元不适用于会产生很高张力的深海系泊系统．肖越[4]应用有限元法，利用索单元模拟系缆，提出频域和时域耦合分析法，考虑了缆索的非线性因素，得出系统的静力和动力响应．余龙等[5]针对深水多成分悬链线系泊系统，首次将缆索重量与经济效益联系起来，结合材料特征提出参数优化设计模型，利用遗传算法得到锚泊线的最佳组成．张素侠[6]针对深海系泊系统的松弛-张紧过程，基于非线性动力学理论，分别建立了静态和动态缆绳模型，运用应力波基本理论中的波动解来求解，得到缆绳内应力波在不同外部条件下的变化规律．刘金沅[7]针对系泊锚链的拉伸和扭转载荷，借助ANSYS软件进行有限元模拟分析，得出残余应力使锚链的疲劳寿命下降为原来的1/10，并且扭矩与轴向拉力、扭转角度呈非线性关系．

上述研究均集中于钢缆的拉伸-弯曲作用，因为国内外学者针对系缆进行分析时，通常基于截面均匀受力假定，将钢缆结构简化为杆、梁单元，忽略了螺旋形钢丝之间的挤压关系．对于复杂的钢制系缆来说，由于受到拉伸-扭转耦合作用，钢缆截面的应力并非均匀分布．本文通过考虑拉伸-扭转耦合作用，对钢缆的具体编制型式进行分析，得到不同编制型式钢缆的扭转特性及动力响应.

1 计算理论与方法

1.1 螺旋钢丝力学平衡方程

基于Costello弹性理论[8]，对钢缆各钢丝的空间结构和受力状态做如下假设：①钢丝的螺旋状态不会受到载荷作用影响；②各螺旋钢丝的轴向拉力、弯曲曲率和扭转角度沿轴线方向保持恒定；③钢丝未受到外部弯矩影响；④忽略钢缆内部的摩擦作用．

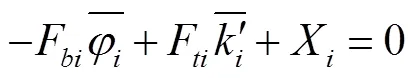
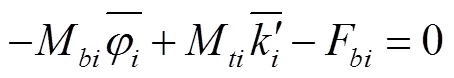
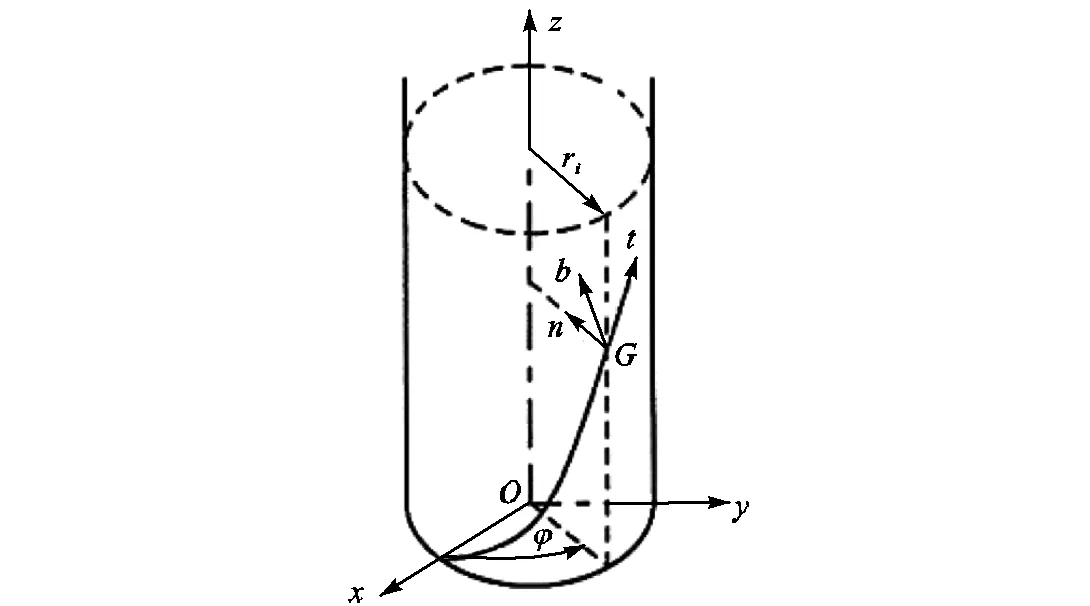
图1 作用于螺旋钢丝上的力和力矩

1.2 6×19型钢缆力学方程

6×19型钢缆结构型式如图2所示，第1股为中心股，第2股为外层股．第1股的3层钢丝分别为钢丝1、钢丝2、钢丝3，第2股的中心钢丝为钢丝4，围绕中心钢丝的为钢丝5、钢丝6．

图2 6×19型钢缆结构示意

对于第2股：

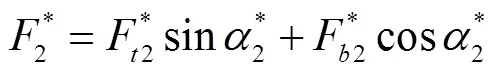
6×19型钢缆力学方程为

其他编制型式钢缆的力学方程推导过程与6×19型钢缆相似．

1.3 钢缆内力计算

钢缆的正应力和切应力分别为

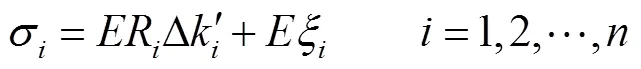
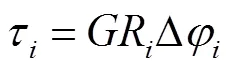
钢丝间的接触方式按照接触区域可分为线接触和点接触两种，如图3所示. 线接触作用发生在第1层和第2层各钢丝接触位置[10-11]，本文假设钢缆内部钢丝材料属性相同，基于赫兹接触理论[12-13]，得出钢丝之间发生线接触的接触力及最大接触应力分别为

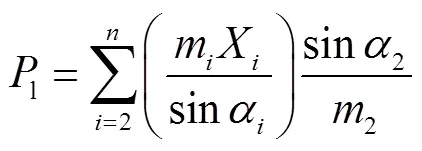
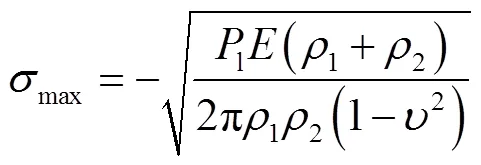
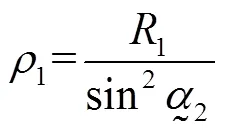
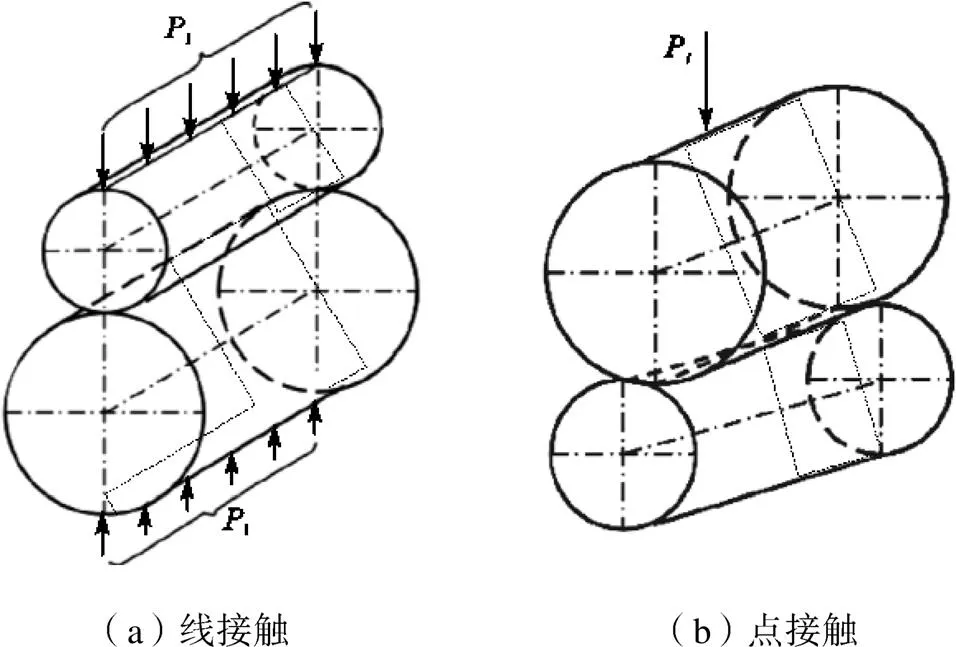
图3 空间两钢丝的接触形式示意

点接触作用发生在外层的相邻钢丝之间[14]，任意两相邻层钢丝间的点接触会形成不连续的网格状接触点[15]，钢丝间发生点接触的接触力及最大接触应力分别为

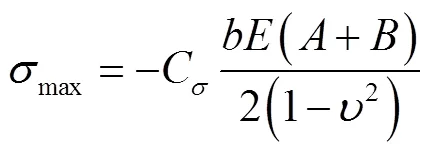
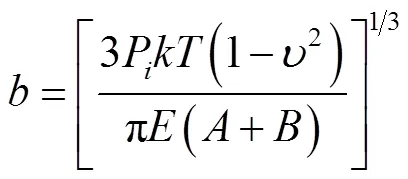
1.4 钢缆动力方程

结合钢缆受到的外载荷作用，基于第1.2节的力学方程，并考虑拉伸-扭转效应建立的钢缆动力方程为

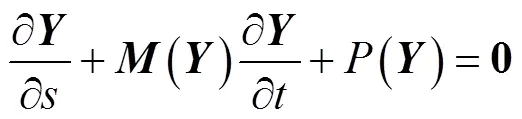
2 钢缆参数

2.1 几何参数

假设各编制型式钢缆均采用相同材料，其参数如表1所示．5层螺旋缆一共有61根钢丝，其几何参数如表2所示[9]．

表1 钢缆参数

Tab.1 Parameters of wire ropes

表25层螺旋缆几何参数

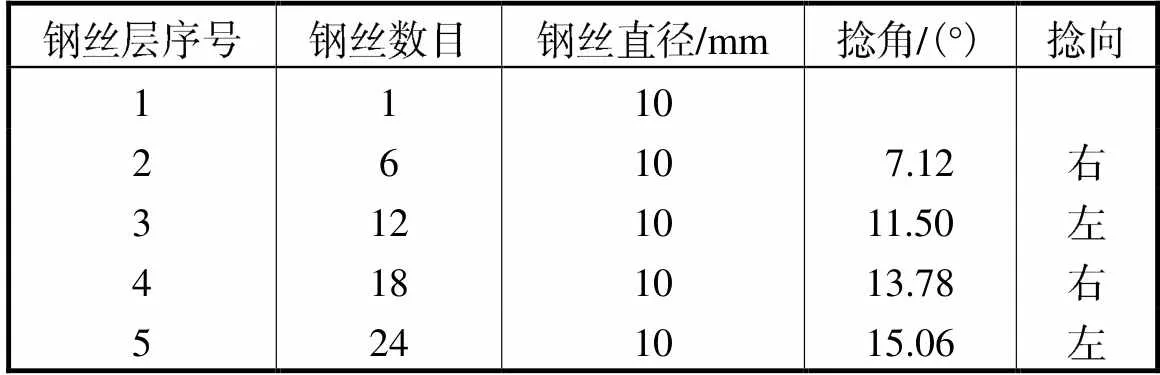
Tab.2　Geometricparametersof 5-layer spiral rope

6×7型钢缆结构如图4所示，表3为其几何参数．6×19型钢缆结构几何参数如表4所示．

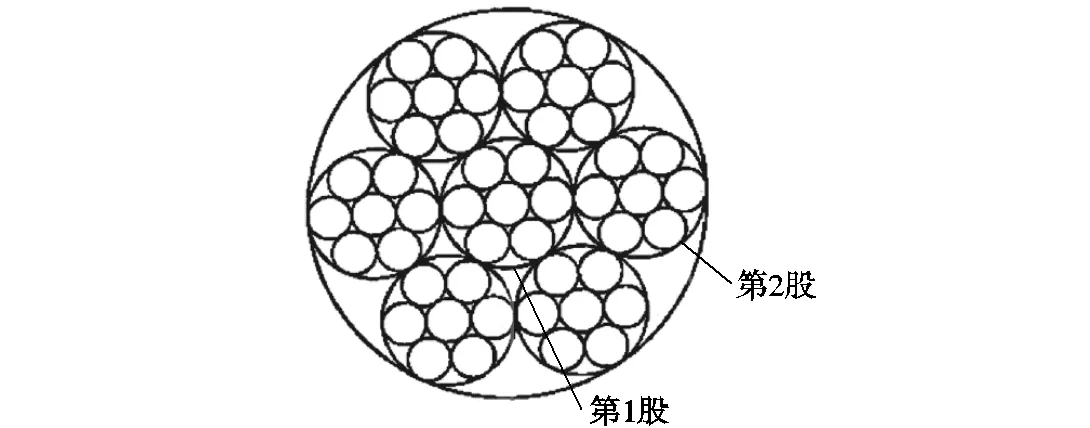
图4 6×7型钢缆结构示意

表36×7型钢缆几何参数

Tab.3　Geometricparametersof type 6×7 rope

表46×19型钢缆几何参数

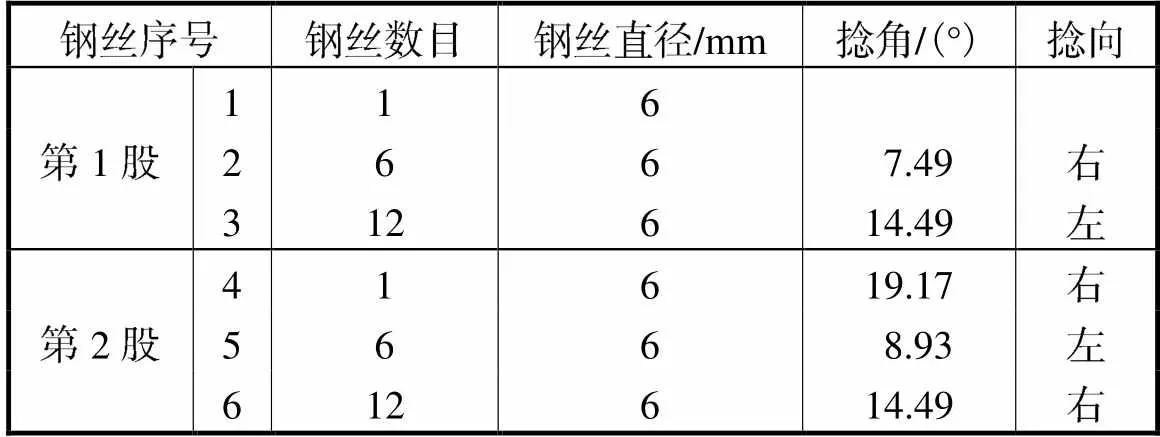
Tab.4　Geometricparametersof type 6×19 rope

2.2 系泊参数

本文的系泊系统参数参考了OC3Spar型浮式风机系泊系统[9, 16]，相关参数如表5所示. 钢缆布置如图5所示，将第1根钢缆沿轴布置，另外两根钢缆与其成120°角．

表5系泊系统参数

Tab.5 Mooringsystem parameters

图5 钢缆布置

3 钢缆运动特性

3.1 5层螺旋缆

本节针对5层螺旋缆的结构型式进行力学性能分析．参考一般海况下钢缆运动的应变结果，取轴向应变为0.0028，将本文解析模型和文献[17]中解析模型的计算结果进行对比，如图6所示．

从图6中可以看出，采用两种解析模型得到的各层钢丝的应变呈现不均匀分布，本文解析模型计算得到的钢缆第1层钢丝的应变与文献[17]相同，第2层至第5层钢丝的应变略小于文献[17]，最大偏差仅为3.5%，可见这两种解析模型的计算结果具有较好的一致性．存在偏差的原因是本文解析模型考虑了钢缆的结构特点和泊松效应，而文献[17]中的解析模型只考虑了相邻层钢丝之间应变和捻角的几何关系. 因此，文献[17]中的解析模型不适用于更复杂的钢缆结构，而本文的解析模型适用于不同编制型式的系泊钢缆内力分析.

图6 轴向应变为0.0028时5层螺旋缆各层钢丝的应变

参考一般海况下钢缆运动的张力结果，取轴向拉力＝1000kN．图7为采用本文解析模型与杆单元计算出的各层钢丝应变结果的对比．从图7中可以看出，本文解析模型由于考虑了拉伸-扭转耦合作用，计算出的各层钢丝应变均高于采用杆单元的计算结果，各层偏差分别为45.93%、43.1%、38.7%、35.6%、33.7%．存在偏差的原因是采用杆单元求解钢缆受力时，假设截面均匀受力．对于实际工程中的钢制系缆而言，由于其内部钢丝相互缠绕的螺旋形空间结构会产生扭转作用，使截面受力不均匀，因此对钢缆具体编制型式的分析十分必要．

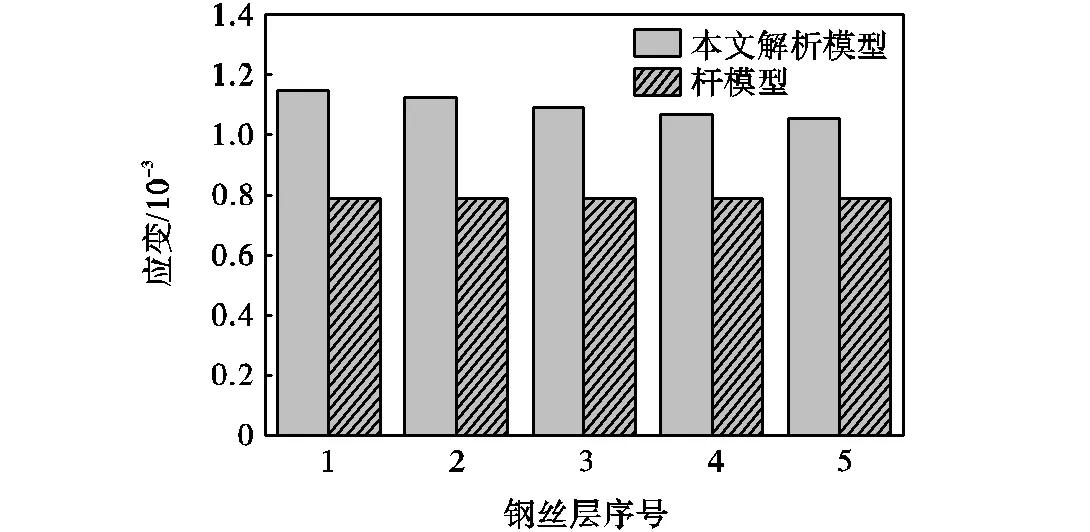
图7 轴向拉力为1000kN时5层螺旋缆各层钢丝的应变

3.2 编制型式对钢缆计算结果的影响

图8为不同编制型式钢缆的最大接触应力随轴向应变的变化．由图8可以看出，钢丝之间的最大接触应力呈非线性变化，当轴向应变小于0.0004时，随着轴向应变的增大，钢丝之间的最大接触应力会迅速增大；当轴向应变大于0.0004时，最大接触应力会随着轴向应变的增大而缓慢增加．这是因为轴向拉伸使得各层钢丝之间以及同层内钢丝之间的挤压效应增强，而接触方式也由最初的点、线接触逐渐转变为面接触，从而增大接触区域的面积，减缓接触应力增大的趋势．5层螺旋缆的最大接触应力位于第2层和第3层钢丝接触处，6×7型钢缆的最大接触应力位于第1股的第1层和第2层钢丝接触处，6×19型钢缆的最大接触应力位于第2股的第2层和第3层钢丝接触处．

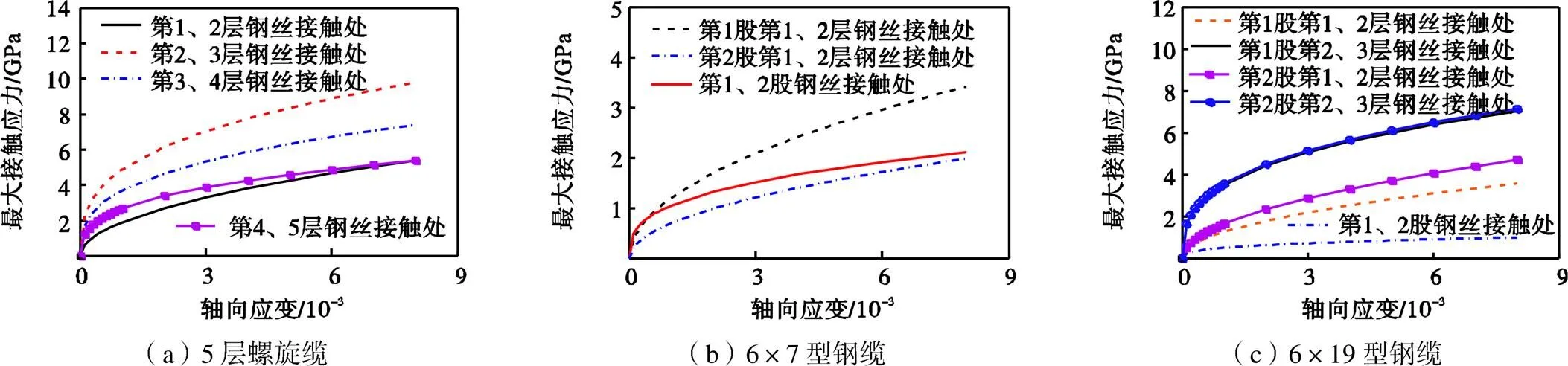
图8 不同编制型式钢缆的最大接触应力随轴向应变的变化

不同编制型式钢缆的轴向力与扭矩随轴向应变的变化如图9所示．可以看出，在相同的轴向应变条件下，不同编制型式钢缆的轴向力不同；对于具体钢缆型式，轴向力随着应变的增加而增大．5层螺旋缆的轴向力最大，6×19型钢缆的轴向力略大于6×7型钢缆．在相同的轴向应变条件下，不同编制型式钢缆的扭矩差别很大；对于具体钢缆型式，扭矩随着应变的增加而增大．

不同编制型式钢缆的轴向应变与扭矩随轴向力的变化如图10所示．轴向力相同时，不同编制型式钢缆的应变不同，6×7型钢缆的应变最大，5层螺旋缆的应变最小；不同编制型式钢缆的扭矩也不同， 6×7型钢缆的扭矩最大，6×19型钢缆的扭矩最小．

考虑到载荷施加的合理性，通过对钢缆结构施加单位长度扭转角，进行扭转力学性能分析．单位长度扭转角作为载荷施加方式可以避免钢缆长度的影响，并且钢缆自身抗扭刚度不会影响扭转角的施加．图11为不同编制型式钢缆的轴向力与扭矩随单位长度扭转角的变化．在相同单位长度扭转角作用下，钢缆的轴向力会随着编制型式的改变而改变，6×7型钢缆的轴向力最大，6×19型钢缆的轴向力最小．不同编制型式钢缆的扭转响应也不同，5层螺旋缆的扭矩最大，6×19型钢缆的扭矩最小．钢丝左捻右捻的交互排列型式会降低钢缆受到扭转时的响应，因此6×19型钢缆由于自身的结构型式特点，在扭转条件下的响应最小．

图9 不同编制型式钢缆的轴向力与扭矩随轴向应变的变化

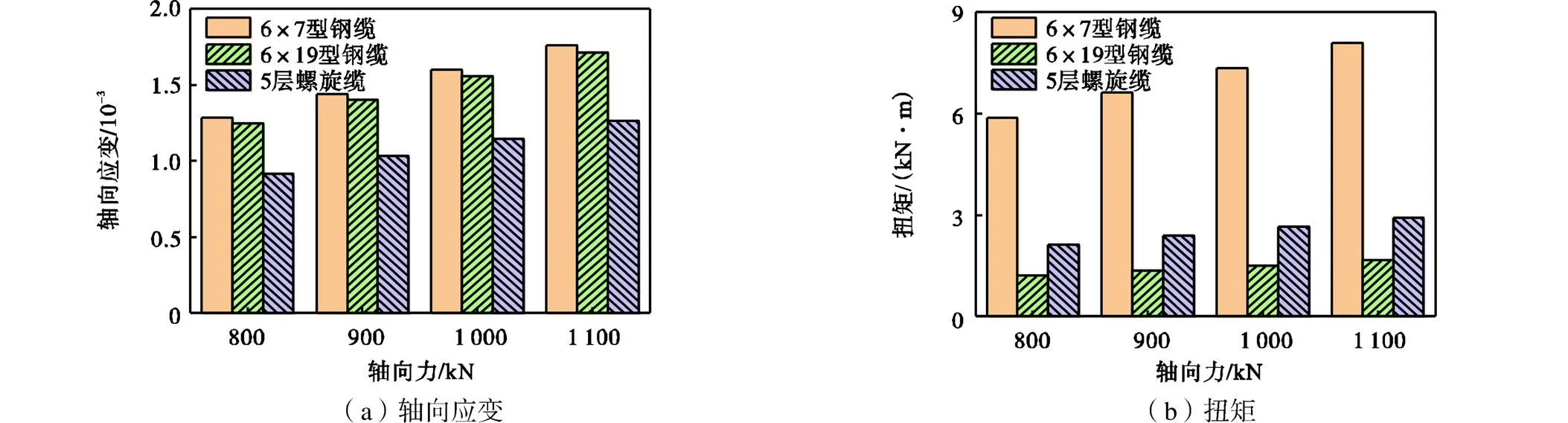
图10 不同编制型式钢缆的轴向应变与扭矩随轴向力的变化

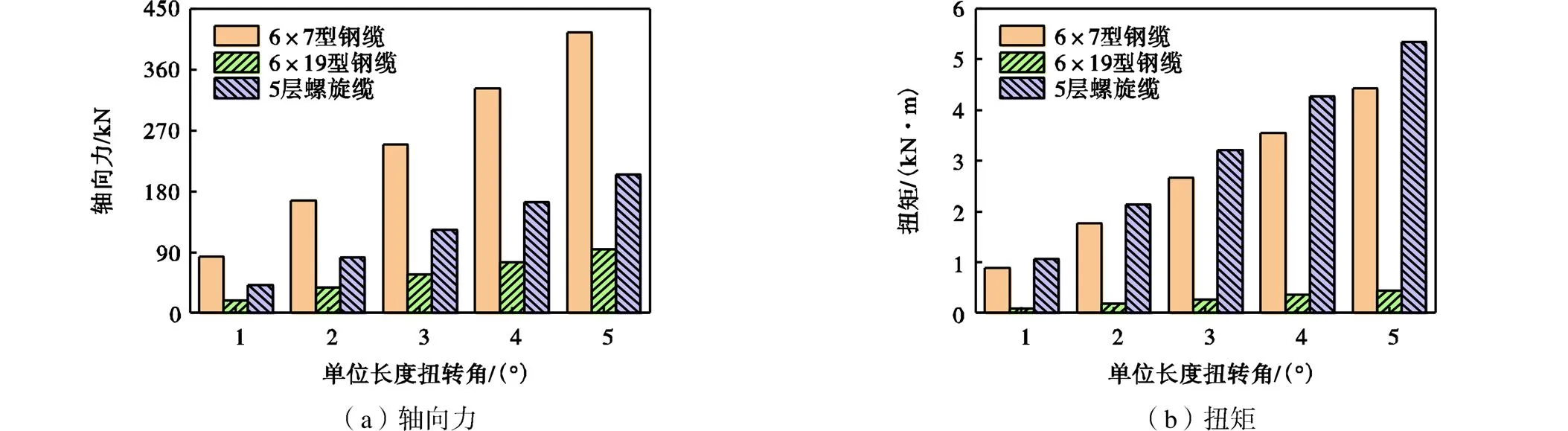
图11 不同编制型式钢缆的轴向力与扭矩随单位长度扭转角的变化

4 钢缆动力特性

4.1 钢缆的静态位形

6×7型钢缆、6×19型钢缆和5层螺旋缆的静态位形如图12所示，在静态位形时钢缆张力沿缆长分布如图13所示．

图12中各种钢缆的静态位形基本一致，可见钢缆的静态位形与编制型式无关．从图13中可以看出，6×7型钢缆和5层螺旋缆的张力分布型式相同，比另两种模型的张力数值大．6×7型钢缆、6×19型钢缆和5层螺旋缆这3种编制型式的钢缆张力都大于忽略扭转特性时的数值，说明编制型式影响钢缆系泊的静态张力．

4.2 钢缆编制型式对张力的影响

对钢缆施加幅值为10m、频率为0.1rad/s的垂直方向正弦激励，其顶端运动响应规律如图14所示. 6×7型钢缆、6×19型钢缆和5层螺旋缆的张力变化趋势与忽略扭转特性时相似，但不同编制型式钢缆的扭矩变化差别很大，6×7型钢缆的扭矩最大.

图12 静态位形

Fig.12 Static configuration

图13 静态位形时张力沿缆长分布

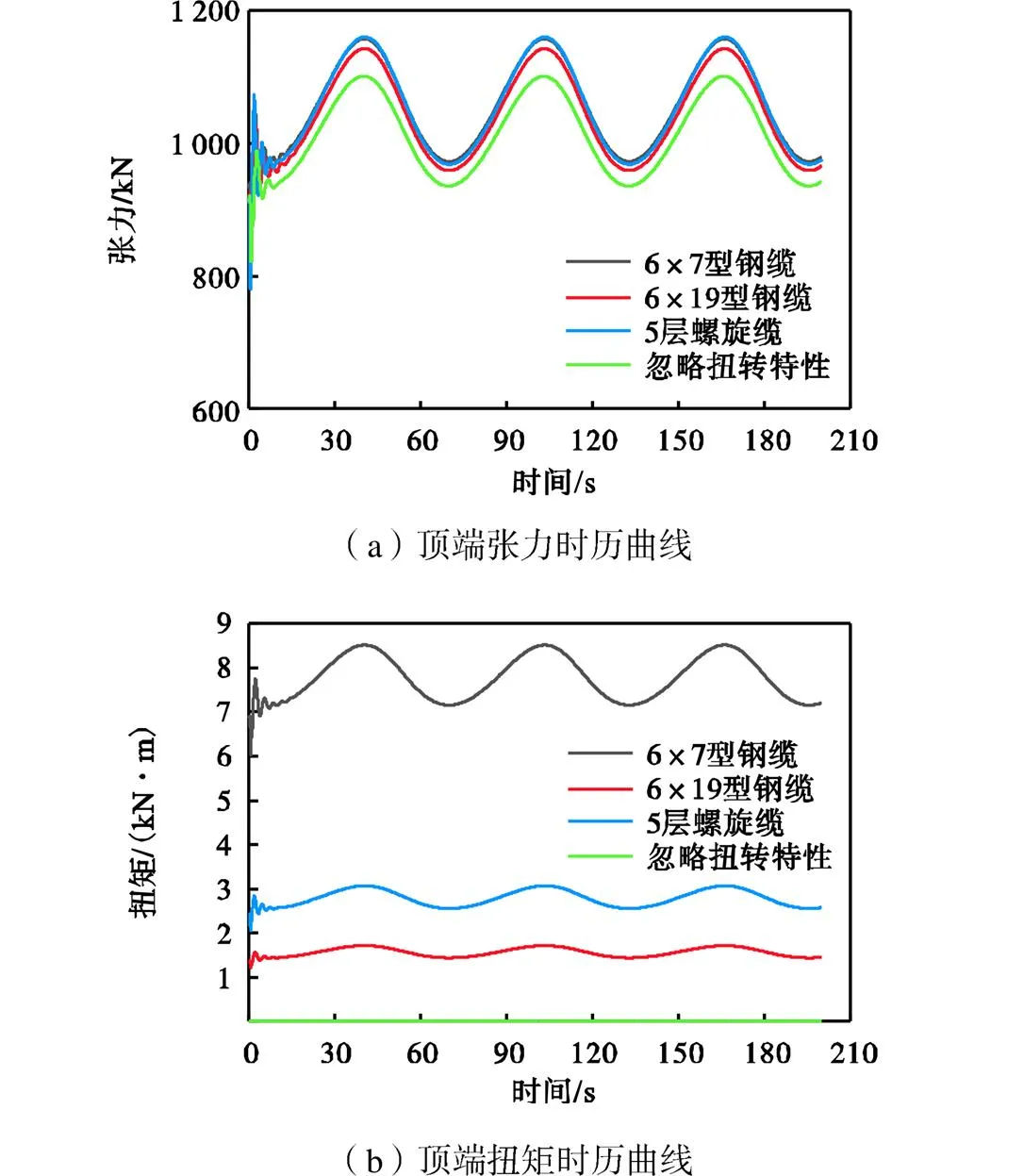
图14 钢缆顶端运动响应规律

不同编制型式钢缆在不同位置的动力响应如图15所示.

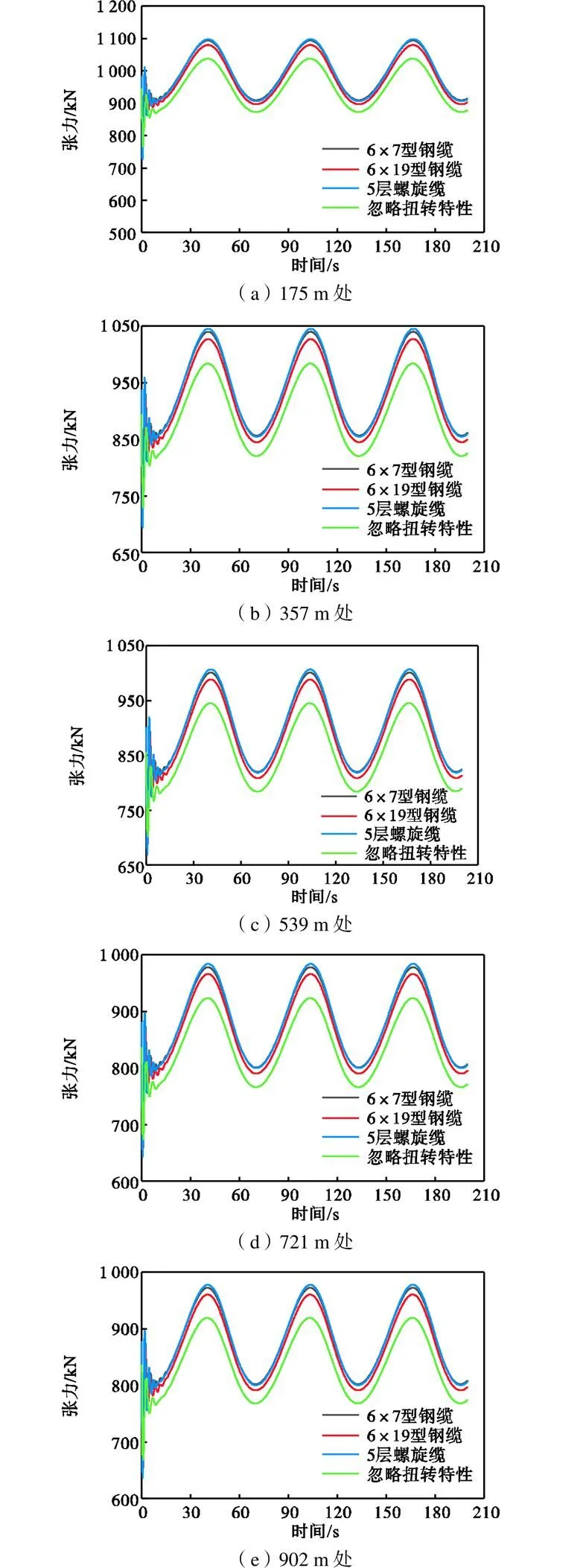
图15 钢缆不同位置处运动响应规律

从图15中可以看出，越靠近钢缆底部，张力最大值越小；相同位置处，5层螺旋缆的张力幅值最大；与忽略扭转特性时相比，考虑编制型式时钢缆张力增大. 图16给出考虑编制型式时钢缆不同位置的张力增加幅度，可见其与编制型式有关，最大张力增加幅度为6.6%.

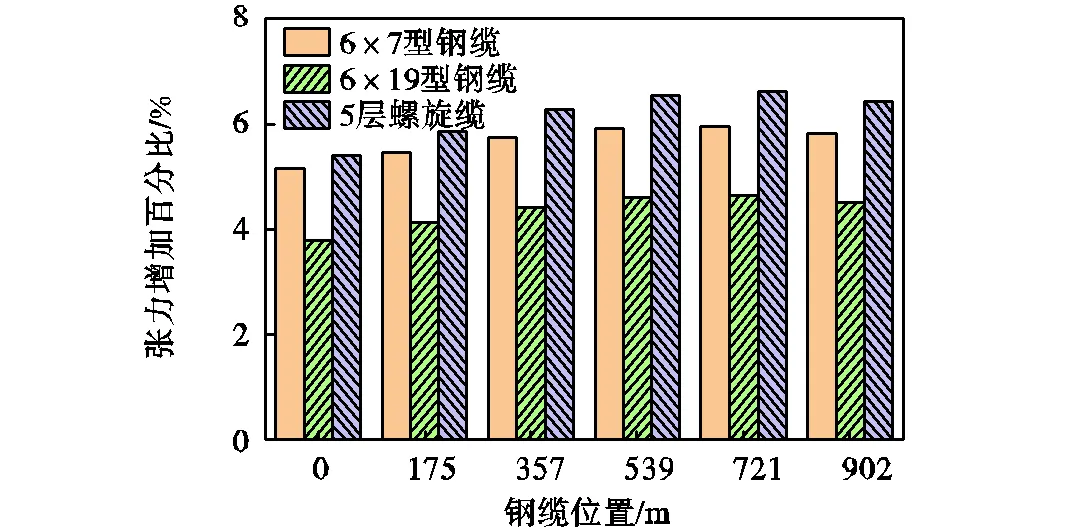
图16 不同编制型式钢缆不同位置处张力增加幅度

5 结 论

本文考虑钢缆的具体编制结构，研究其在外载荷作用下的几何形态，建立了不同编制型式钢缆(6×7型钢缆、6×19型钢缆、多层螺旋缆)的力学模型. 基于非线性动力学理论，考虑外载荷及钢缆自身的拉伸-弯曲-扭转特性，建立了钢缆动力学方程组，提出深海系泊钢缆的动力分析方法，得出以下结论.

(1)利用本文解析模型得出的轴向应变比利用杆单元计算的结果大，最大偏差为45.93%，说明对于内部钢丝相互缠绕的复杂钢缆，截面受力并非均匀，对钢缆编制型式的分析极为必要.

(2)钢缆各钢丝之间的最大接触应力会受到编制型式的影响，应根据钢缆的具体编制型式分析接触应力作用.

(3)在相同扭转条件下，不同编制型式钢缆的轴向力和扭矩响应不同. 6×19型钢缆由于自身钢丝左捻右捻的交互排列型式，受到外载荷时，扭矩响应会比另外两种结构型式低.

(4)考虑编制型式时钢缆结构的系泊张力值会比忽略扭转特性时有所增加，并且增加幅度与编制型式有关，最大增幅为6.6%. 因此，在计算钢缆张力时，应考虑编制型式.

［1］ Ridge I M L. Tension-torsion fatigue behaviour of wire ropes in offshore moorings[J]. Ocean Engineering，2009，36(9/10)：650-660.

［2］ Kim Nam-Il，Jeon Sang-Soo，Kim Moon-Young. Nonlinear finite element analysis of ocean cables[J]. China Ocean Engineering，2004，18(4)：537-550.

［3］ Zhu Z H，Meguid S A. Elastodynamic analysis of low tension cables using a new curved beam element[J]International Journal of Solids and Structures，2006，43(6)：1490-1504.

［4］ 肖 越. 系泊系统时域非线性计算分析[D]. 大连：大连理工大学船舶工程学院，2006.

Xiao Yue. Nonlinear Time-Domain Analysis and Calculation for Moored Systems[D]. Dalian：School of Naval Architecture and Ocean Engineering，Dalian University of Technology，2006(in Chinese).

［5］ 余 龙，谭家华. 深水多成分悬链线锚泊系统优化设计及应用研究[J]. 江苏科技大学学报：自然科学版，2004，18(5)：8-13.

Yu Long，Tan Jiahua. Research and application of optimum design of multi-component mooring line[J]. Journal of East China Shipbuilding Institute：Natural Science Edition，2004，18(5)：8-13(in Chinese).

［6］ 张素侠. 深海系泊系统松弛-张紧过程缆绳的冲击张力研究[D]. 天津：天津大学建筑工程学院，2008.

Zhang Suxia. Study on Snap Tension of Taut-Slack Mooring Lines in Deep Water[D]. Tianjin：School of Civil Engineering，Tianjin University，2008(in Chinese).

［7］ 刘金沅. 锚链腐蚀磨损累积损伤评估方法研究[D]. 大连：大连理工大学船舶工程学院，2013.

Liu Jinyuan. Research on Approach for Corrosion and Wear Cumulative Damage Assessment of Chain Links[D]. Dalian：School of Naval Architecture and Ocean Engineering，Dalian University of Technology，2013(in Chinese).

［8］ Costello G A. Theory of Wire Rope[M]. New York，USA：Springer Verlag，1997.

［9］ 赵凤帅. 考虑缆索编制型式的钢制系缆拉伸-扭转动力响应研究[C]// 中国海洋工程学会第19届中国海洋(岸)工程学术讨论会论文集(上). 南京，2019：102-109.

Zhao Fengshuai. Dynamic response of different types of steel mooring lines considering tension and torsion effects[C]. Proceedings of the 19th China Ocean(Off-shore)Engineering Symposium(Part I). Chinese Ocean Engineering Society. Nanjing，2019：102-109(in Chinese).

［10］ Kumar K，Cochran J E. Closed-form analysis for elastic deformations of multilayered strands[J]. Journal of Applied Mechanics，1988，54(4)：898-903.

［11］ Kumar K，Botsis J. Contact stresses in multilayered strands under tension and torsion[J]. Journal of Applied Mechanics，2001，68(3)：432-440.

［12］ 孔祥安，江晓禹，金学松，等. 固体接触力学[M]. 北京：中国铁道出版社，1999.

Kong Xiang’an，Jinag Xiaoyu，Jin Xuesong，et al. Solid Contact Mechanics[M]. Beijing：China Railway Publishing House，1999(in Chinese).

［13］ Johnson K L. Contact Mechanics[M]. Cambridge，UK：Cambridge University Press，1996.

［14］ Pilkey W D. Formulas for Stress，Strain，and Structural Matrices[M]. New Jersey，USA：John Wiley & Sons，Inc. ，2005.

［15］ 于春蕾. 单股钢丝绳力学性能高效数值模拟技术研 究[D]. 秦皇岛：燕山大学机械工程学院，2017.

Yu Chunlei. Research on Efficient Numerical Simulation Technique for Mechanical Behavior of Wire Strands[D]. Qinhuangdao：School of Mechanical Engineering，Yanshan University，2017(in Chinese).

［16］ Jonkman J. Definition of the Floating System for Phase IV of OC3 [R]. Golden，USA：National Renewable Energy Laboratory，2010.

［17］ 谢桥漾. Galfan拉索应力分布规律研究[D]. 北京：北京交通大学土木建筑工程学院，2016.

Xie Qiaoyang. Research on the Stress Distribution of Galfan Cable[D]. Beijing：School of Civil Engineering，Beijing Jiaotong University，2016(in Chinese).

Dynamic Response of Different Types of Mooring Wire Ropes

Zhang Ruoyu1, 2，Zhao Fengshuai1, 2，Lin Fengmei3，Qie Yake3，Li Yan1, 2

(1. School of Civil Engineering，Tianjin University，Tianjin 300072，China；2. Tianjin Key Laboratory of Port and Ocean Engineering，Tianjin University，Tianjin 300072，China；3. Juli Sling Co.，Ltd.，Baoding 072550，China)

Given that the torsion characteristics of rope have seen little research domestically，in this paper，tension-torsion models of different types of wire ropes were established. The basic characteristics of wire rope structure and steel wire material were analyzed，including the force of wire ropes in marine engineering. Based on reasonable assumptions，the stress distribution of wire ropes was simplified into a geometric problem，and the response characteristics of wire ropes under the joint action of tension and torsion were determined. In view of the different contact characteristics between steel wires，the Hertz contact theory was incorporated into numerical simulation of wire ropes，and the method of contact stress solutions of point and line contact was established. Based on the theory of nonlinear dynamics，the coupling terms of tension，bending and torsion were introduced into the stiffness of wire ropes，and the equations of dynamic equilibrium were derived. A model for the calculation of a mooring system was established to obtain the rope dynamic response under the external load. The influence of the torsion of the rope on the tension under axial load was analyzed. The influence of torsion on the internal force of the rope was also studied，and a law of tension variation was established. Study results showed that the response of different types of wire ropes，including the tension value，varied under the same axial load. Compared with the values obtained when torsion was neglected，the tension values calculated for the different rope types were larger and varied by rope type. Cross-sectional stress distribution was not uniform for the different types. The distribution of internal stress in wire rope was closely related to the type of rope，so it is very important to consider the specific type in the calculation of stress，especially in the analysis of contact stress. The 6×19 type had a lower response when subjected to external load due to the alternating arrangement of left and right twisting.

mooring wire rope；dynamic response；tensile-torsional characteristic；type of wire rope

the National Natural Science Foundation of China(No.51509185).

10.11784/tdxbz201905035

P751

A

0493-2137(2020)08-0872-09

2019-05-13；

2019-10-15.

张若瑜（1981—  ），女，博士，副教授.Email：m_bigm@tju.edu.cn

张若瑜，zryu@163.com.

国家自然科学基金资助项目(51509185).

(责任编辑：刘文革，樊素英)