多元研读促设计深入理解创灵动

2020-06-03高晖

云南教育·小学教师 2020年8期

关键词：数形人教版正方形

高晖

研读教材一直是教师工作的重要内容，它关系到教师的课堂设计、课堂组织与实施，更关系到教学目标的实现、教育目标的达成。教材也是学生从事数学学习的基本素材，它为学生的数学学习活动提供了基本线索、基本内容和主要的数学活动机会。

本文以人教版数学六年级上册“数学广角——数与形”为例，通过发现、质疑、创造式的多元化研读方式和对教材纵横向对比联系，将教学设计做了大刀阔斧的“改革”。

一、内容背景的发现与渗透

人教版数学六年级上册“数学广角——数与形”例1的教学内容是：

基于小学生的年龄特征和认知特点，教材编排时通常只呈现相应知识点以及相关数学思想方法的渗透，而知识点背后一些深层次的原理或相关背景等教材在编排时进行了取舍。研读教材时如果能挖掘发现这些背后隐藏的部分，从而可以让教师立足于“高观点”理解教材。

例1是让学生运用数形结合探究“正方形数”的规律。“正方形数”“三角形数”等统称为“形数”。古希腊毕氏学派对“形数”就已经有着深入的研究。基于此背景，设计时我在开篇加入了毕氏学派“万物皆数”思想和“形数”的介绍，让学习建立在数学史的基础上了解知识的产生和发展的过程，激发学习数学的兴趣。

二、内容编排的对比与联系

“数与形”的内容是2013年人教版义务教科书修订版新增的内容，而在北师大版数学五年级上册“数学好玩”的板块中编排了“点阵中的规律”。（如下图）

两个版本的编排设计有着异曲同工之妙，人教版“以形助数”，北师大版“以数解形”。通过对比和联系两个版本教材的编排，我将北师大版点阵中的规律和“形数”相结合，形成教学设计。

片段一：

（课件出示：9）

师：同学们还记得刚才老师介绍时9所代表的含义吗？

生：理性。

师：在研究9的时候，学者捡了9颗石子并摆成了一个我们很熟悉的图形，猜猜是什么图形？

生：三角形，正方形……

师：用你们手中的围棋子试着摆一摆。

生：正方形。

师：观察这个图形，你能从中发现与9相关的一些算式吗？

生：3×3=9，1+3+5=9，1+2+3+2+1=9…

师：从这些算式中，你发现什么特点？

生：3×3就是3的平方，1+3+5是连续的奇数相加，1+2+3+2+1是连续自然数再倒回去相加……

师：当时学者们也发现了这样的特点，1+3+5=3×3=32=9。

师：你们还能找到和9有着相同特点的数字吗？

生：1=1×1=12=1，1+2=2×2=22=4，1+3+5=3×3=32=9…

师：观察这些算式，你能发现什么规律吗？

生：从1开始的连续奇数的和等于奇数个数的平方。

师：1、4、9、16…这些数字学者们还给它们起了个名字——“正方形数”。

数形结合思想的运用可以说一直贯穿于小学数学的学习中，在学生已经拥有了很多数与形结合的经验后，通过观察和计算1、1+3、1+3+5、1+3+5+7…既能发现加数的规律（从1开始的连续奇数相加），又能发现和的规律（都是连续的正方形数），在发现规律的基础上，通过推理，再引导学生把规律应用于一般的情形，解决问题。

三、内容资源的选择与整合

创造性地使用教材，做到尊重教材和灵活处理教材，充分发挥教材资源作用，有机结合教材的例题资源和练习资源等可以让教学设计更加灵动。设计中，我将例1和教材第109页练习二十二的第2小题结合，进一步对“形数”进行探究，深化数形结合思想。

片段二：

课件出示：10

师：它代表什么含义？

生：完美。

师：你能用刚才的方法发现10的特点吗？

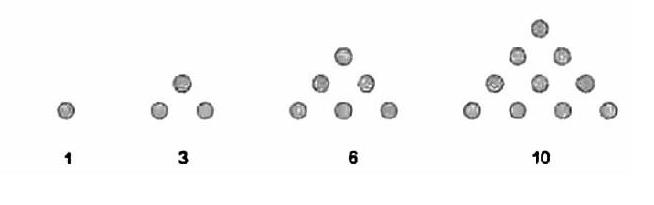
生：我们把10颗棋子摆成了一个三角形，从而得到10=1+2+3+4，是连续自然数的和。

师：还有和10有着一样特点的数吗？

生：还有1、3、6、15…都可以写成连续自然数的和。

师：你们能给这些数也起一个名字吗？

生：三角形数。