基于改进的角度偏差法算法的激光测量数据精简

（湖南工业大学 机械工程学院，湖南 株洲 412007）

1 研究背景

目前，激光测量凭借其可靠性高、测量环境适应性好等特点而被广泛用于高精度加工领域。激光测量会产生大量数据，测量点分布密集，能有效勾勒出测量物的轮廓形状并反映细节特征，但处理过多的数据点会占用计算机大量内存，导致计算机的运行速度缓慢。实际上，不是所有数据点都是有用信息，而且数据存储或显示都将消耗大量的时间和计算机存储空间，所以在保证精度的前提下，对测量数据进行精简显得尤为重要。

在精简数据方面，许多国内外的专家学者对激光测量数据精简问题进行了一系列研究，并取得了较多的研究成果。目前常用的数据精简方法主要有包围盒法[1]、非均匀网格法[2]、最大（小）距离法[3]、角度偏差法[4]、三角网格法[5]、弦高偏差法[6]等。同时，有专家学者开始对数据精简算法加以改良，如付玮等[4]提出了一种基于局部和全局点云特征相融合的简化算法，通过基于点云的网格分割非均匀网格法来提取局部点云特征；吴凤和等[7]在考虑曲线曲率变化的基础上构建了弦高函数，并通过迭代得到各测点变化的弦高值，再根据弦高法的数据精简原则确定需要保留的测量点。

其中，角度偏差法被广泛应用并加以改良。角度偏差法以连续点之间夹角为准则精简数据，能够保留轮廓特征和一些细节特征，但其存在一定的缺陷。针对角度偏差法的缺陷，方源敏等[8]对其采取设立平均偏角阈值去除偏角较小的数据点的方法进行改进，解决其易出现断点问题。为优化其精简效果，洪军等[9]提出角度弦高法，利用包围盒法构造分割面，并利用分割面将数据点云处理成按扫描线存储的“结构化”测量数据，再利用角度-弦高联合准则法逐线精简。但以上研究均是从某一方面改进角度偏差法，未能有效地保留一些细节特征，且未考虑到角度偏差法不能保留一些大曲率点这一缺陷，而曲率较大的点会包含较多的特征信息[10]，这些点对模型的构建具有十分重要的意义。

基于以上这些原因，本文针对角度偏差法存在的缺陷进行改良，在此基础上提出角度距离法，该方法将随着数据点的曲率大小而变化的角度阈值作为数据精简准则，同时考虑到点与点之间的最小距离，从而保留一些大曲率的数据点，防止断点的出现，以保留好原物的细节特征。通过联立两种测量数据精简准则，使数据点精简后的疏密随曲率变化而变化，从而具有一定的自适应性。

2 数据精简效果评判准则的建立

数据精简的目的在于去除无用数据点，进而利用最少的离散点就能达到全面而准确地表示空间复杂实体原有信息，并在此基础上追求更快的建模速度。点云数据（激光测量数据点集，以下简称点云数据）精简效果的评判主要从精简率、精度和精简时间3个方面来衡量[11]。

1）精简率。即被去除数据点数与原始数据点数的百分比，精简率反映了精简算法对无用数据点的去除程度。需要指出的是，精简率不是越高越好，有时数据点数过少会给后续建模(例如三角网格化)带来困难，因此应根据实际需要选择合适的精简率。

2）精度。即精简后的点云数据构建的三维模型与原始三维模型之间的误差，精度要求精简后的点尽可能地保留原始点云细节特征，它为衡量精简效果最重要的准则。常用的具体指标有长度、表面积、截面面积、体积、饱满度和拟合曲线误差等。

3）精简时间。即精简数据所需的时间，其精简数据耗费时间要尽可能短。

然而，在实际实验中很难三者兼顾，故精简的最佳效果是精简后的点云能用较少的数据点构建模型、保留细节特征且精简时间不太长。达到文献[9]中所述的效果，即数据点在精简后的疏密应该随着曲面曲率的变化而变化，曲率变化越大，数据点越多；曲率变化越小，数据点越少。此外，可根据各自算法特点建立相应的精简效果评判准则。

3 改进数据精简算法原理

3.1 角度偏差法原理

角度偏差法的原理在于引入一个角度偏差值Δa来判读数据点是否保留，即设立一角度阈值Δa，再取一条曲线，令第二个点为基准点，命名为P2，将其前后相邻的点命名为P1与P3；比较向量之间的夹角a2与Δa的大小，当a2＜Δa时，去除该点。然后连接后续点继续进行角度比较，直到a2≥Δa时，保留该点；令P3为新的基准点，重复上述步骤直到测量点均已处理完毕，其原理示意图如图1所示。

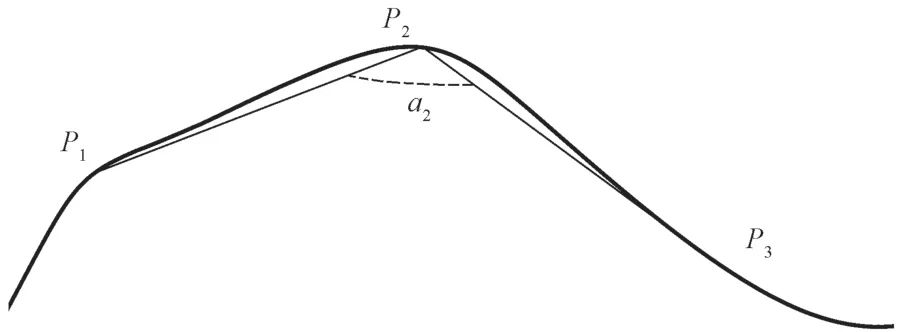
图1 角度偏差法示意图Fig.1 Schematic diagram of the angle deviation method

角度偏差法利用了反映曲面变化的特征参数曲线角度作为数据精简的准则，能够保留数据的一些特征，且一般对已经结构化的点云数据适用性较佳，如曲线的整体轮廓。但当曲线较为平坦时，存在曲率较小而角度可能较大的情况；同样，当相邻点相距较近时，也会存在使曲率较大而角度可能很大的情况。因此，曲率与角度作为衡量数据点所含信息多少的准则，在角度偏差法中无法和谐统一。同时，角度偏差法容易出现局部区域有空白断点的情况，且存在对数据曲率变化的点精简适应性不强的缺点。

3.2 角度距离法原理

为弥补上文所述的角度偏差法的缺陷，依据点云数据的特点设计出角度距离法，此算法逐点针对角度偏差法的缺陷，提出改良方法，改良的具体过程如下文所述。

传统角度偏差法无法将点的曲率与角度相统一作为精简数据的准则，因为传统的角度偏差法在设立角度阈值Δa时未考虑到点曲率因素导致问题的出现。为解决这一问题，现将角度阈值Δa与点的曲率大小相结合，建立新的角度阈值Δai，计算方程如下：

式中：ki为点Pi的曲率值，i=2,3,…,n；

Δa为开始设定的角度阈值。

由式（1）可以得知，当某点的曲率值较大时，其对应的角度阈值Δai会相对变小，使得此点能容易被保留下来；反之，当某点的曲率值较小时，此点会被去除。通过这种方法可以对数据点进行筛选，保留曲率值较大的点。

同时，针对传统角度偏差法会出现局部空白断点的弊端，采取设置最小的距离阈值d来解决，将相邻两点间距离大于阈值d的点保留。通过设立一个较小的最小距离阈值来保留测量数据点之间距离较大的点，防止局部断点的出现，d的取值大小为

σ为方差；

λ为比例系数，可通过改变λ的大小来调整阈值的大小，进而达到理想的精简效果。

最后，针对传统角度偏差法对测量数据点曲率变化的自适应力较差的问题，角度距离法采取将带有自适应属性的角度阈值Δai和最小距离d联立作为精简数据的衡量准则，其原理示意图如图2所示。

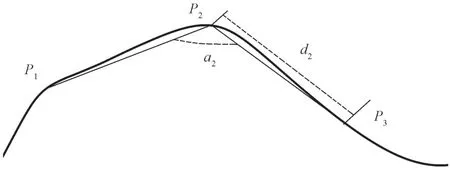
图2 角度距离法原理示意图Fig.2 Schematic diagram of the angle distance method

具体算法精简过程如下：

1）设定角度阈值Δa和距离阈值d；

2）选取一条曲线，并计算曲线上每个点的曲率；

3）选取曲线上第二点为P2，其左右两点为P1和P3；

4）判断曲线上的点是否处理完毕，若处理完毕，转步骤8；若未处理完毕，接步骤5；

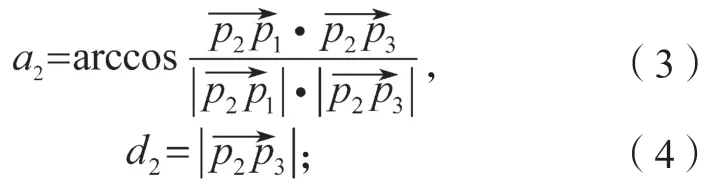
6）判断是否满足条件a2≥Δa或d2≥d，若满足条件，则P2为保留点，后令P3=P2，其左右的点为P1和P3，后接步骤7；若不满足条件，则说明P2为去除点，后令P3=P2，其左右的点为P1和P3，转步骤4；

7）判断曲线上的点是否处理完毕，若处理完毕，接步骤8；若未处理完毕，转步骤5；

8）精简完毕。

4 实验结果与分析

4.1 原始数据分析

以委托英国真尚有限公司设计生产所得的激光测量仪对某管道进行轮廓测量，其测量精度不超过±0.02 mm。现对管道某一截面进行测量，获得原始测量数据后，选取部分数据（选取部分数据点为705个）滤波去噪处理后分析其特点，如图3所示。

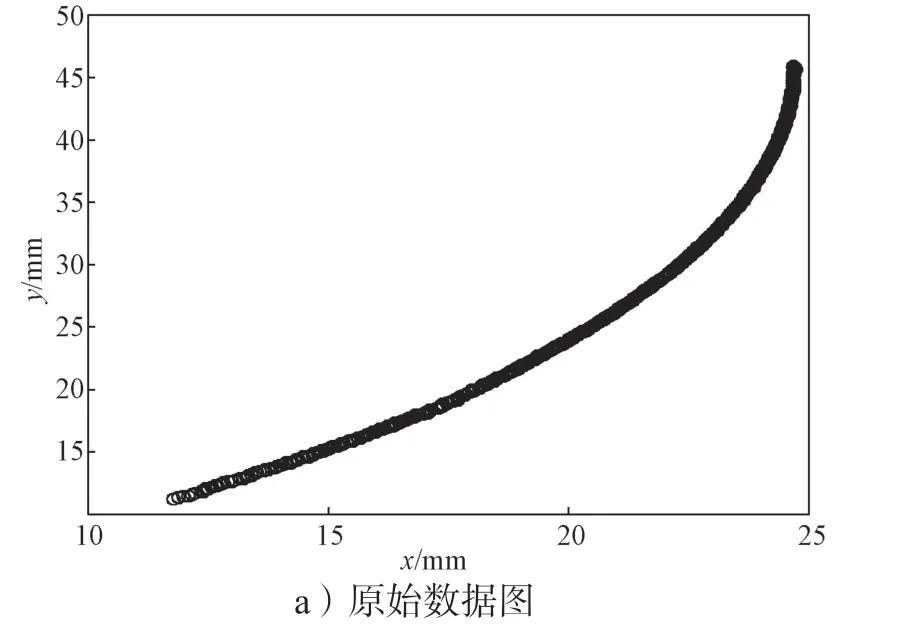
图3 原始数据点、局部放大及曲率变化图Fig.3 Diagram of original data points,local magnification and curvature change

由图3可以看出，原始数据是管道轮廓截面的一片段，测量点分布较密集，点密度约为每毫米15.6个且曲率较大段的点分布更密集。从局部放大图中可以看到轮廓表面凹凸不平的细节特征，细节特征能反映表面的粗糙程度等信息。同时，从曲率变化图3c来看，原始数据曲率值的整体趋势从左到右依次由小变大，除去部分曲率变化异常的点外，曲率变化基本在0.025～0.5 范围之内。这些信息能有效勾勒出管道的部分轮廓形状。

4.2 精简效果对比分析

借助上文的原始数据，在Matlab 软件平台上，利用角度偏差法与角度距离法两种算法对原数据进行精简处理，其精简结果如图4～5和表1～2所示（其中，角度偏差法的角度阈值Δa=2.90，角度距离法的阈值Δa2=2.90，d=0.062 mm）。

为验证曲率角度法的精简效果，将精简率、精度和精简时间3方面指标作为精简效果的评价准则，首先，对原始数据的曲率进行计算，将曲率值大的点作为标记点并记录其数量；之后统计精简后被标记点的数量，对比前后标记点的数量，两者数量越靠近，说明算法对数据大的曲率点的保留效果越好，以此为参考反映出算法对数据精简曲率与角度的统一。

图4 角度偏差法精简效果与局部放大图Fig.4 Reduction effect of the angle deviation method with a local magnification

由图4可知，角度偏差法能够较完整地反映管道部分轮廓形状。虽能够做到数据点在精简后的疏密应该随着曲面曲率的变化而变化，但其对曲率较小的线段数据点去除较多导致局部断点的出现，从而影响轮廓形状的完整性。

对比图3b和图4b所示的局部放大图。可知在局部细节保留上角度偏差法丢失严重，未能保留好轮廓的一些细节特征。图5为角度距离法的精简效果和局部放大图。

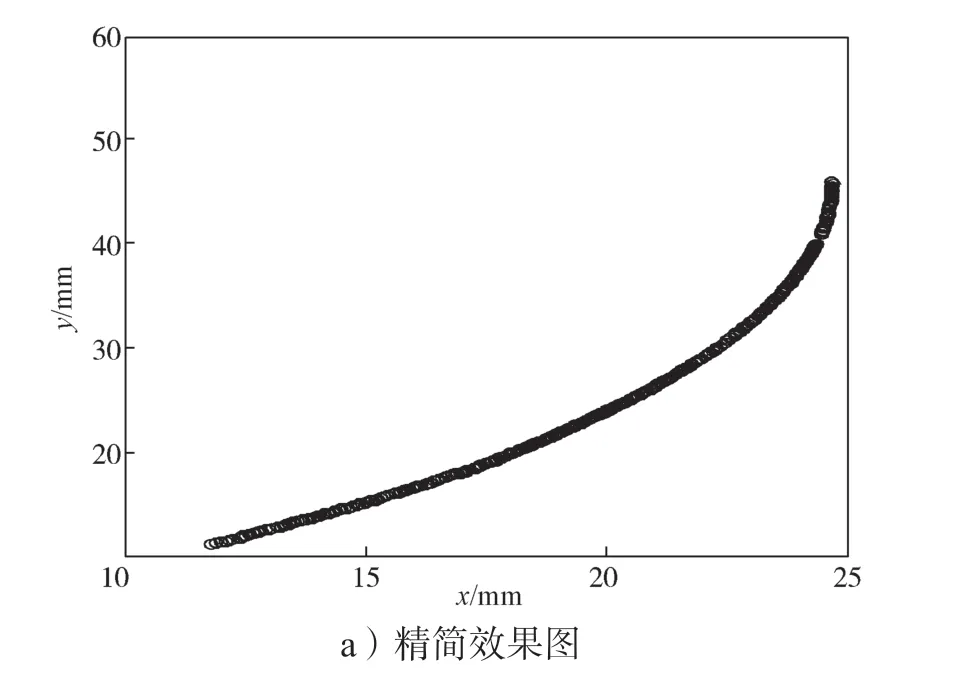
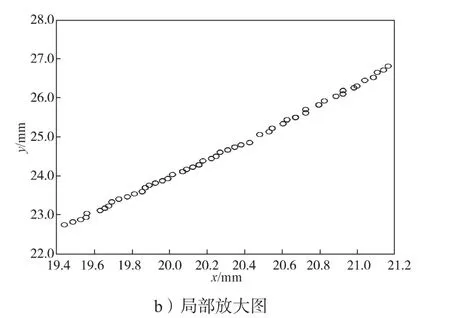
图5 角度距离法精简效果与局部放大图Fig.5 Reduction effect of the angle distance method with a local magnification

由表1和图5可以得知，从精简效果来看，角度距离法能够完整地反映管道的部分轮廓形状，并且改正了角度偏差法出现局部断点的缺陷。对比图3b和图5b所示的局部放大图，可知角度距离法在细节特征保留上远优于角度偏差法保留的细节特征。在保留曲率较大的标记点方面，角度偏差法未能完整保留这些标记点，而角度距离法能完整保留28个被标记的点，弥补了角度偏差法不能保留一些大曲率点的这一缺陷。精简后的数据点分布随着曲面曲率的变化而变化，这说明其对存在一定曲率变化的数据有一定的自适应能力。角度距离法能够有效改进角度偏差法的一些缺点，以下从精简率、精度和精简时间3方面来对比分析两种算法的优劣。

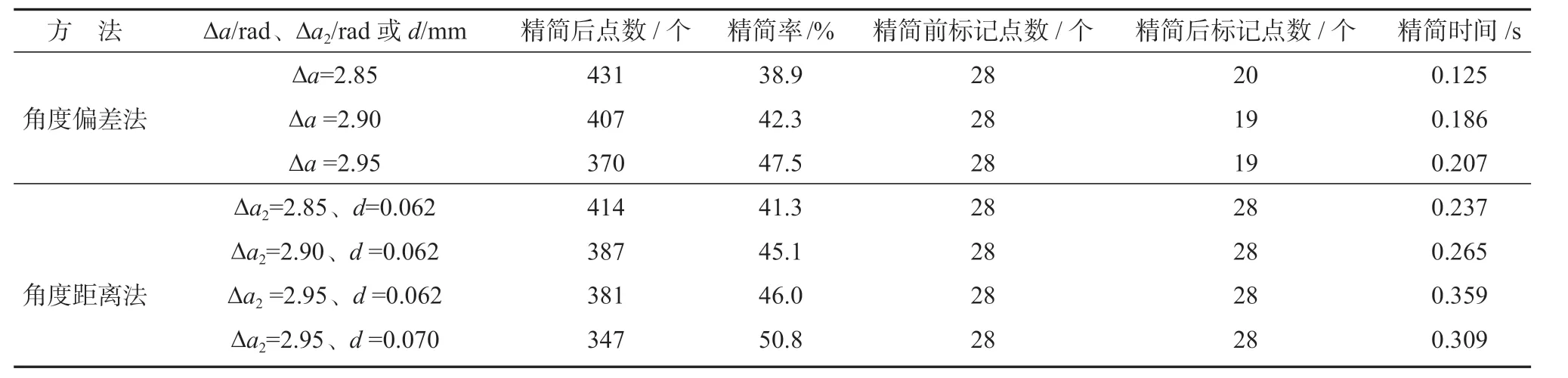
表1 精简结果对比表Table1 Results comparison table

1）精简率。对比两种方法的精简率，可知在角度阈值相同时，角度距离法的精简率高于角度偏差法的，且可通过修改阈值参数来改变其精简率，达到实际需要的精简效果。

2）精简时间。在精简时间方面，角度偏差法优于角度距离法，本文算法在精简时间上约慢0.1 s，其精简时间能够满足实际要求。

3）精度。两者的精度对比如表2所示，在精度对比中，角度距离法在曲线长度以及拟合曲线标准差中均优于角度偏差法。

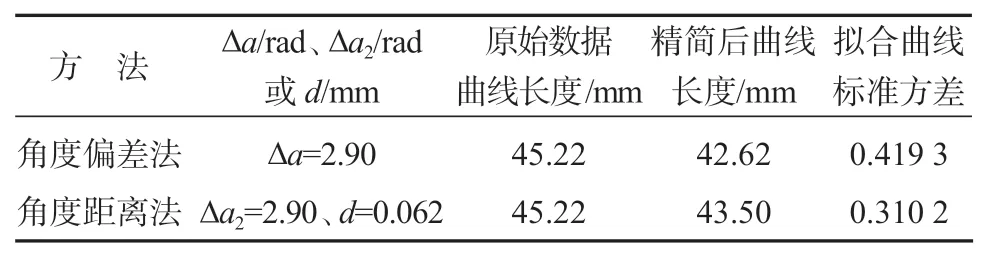
表2 精度对比表Table2 Precision comparison table

5 结论

本文针对传统角度偏差法存在的缺陷，提出了一种角度距离点云数据简化方法，对测量数据进行精细精简处理。即将点曲率大小融入角度偏差法，同时设置最小距离阈值以防止精简时出现局部断点，将角度与距离作为精简数据的准则，保留数据测量点。

通过实验结果与分析可以得知，所提出的改进的角度偏差法算法能够完整地保留被标记的大曲率点，并且能避免出现局部断点，能够保留轮廓的细节特征，达到数据点在精简后的疏密应该随着曲面曲率的变化而变化的要求。

与传统的角度偏差法对比精简效果，可知所提出的角度距离法不仅在精简率与精度方面均优于角度偏差法的，而且可以通过修改阈值选取合适的精简率，但是其在精简时间上耗时稍长，这将是此算法下一步改进的方向。