A novel Omega-driven dynamic PANS model *

Chao-yue Wang, Fu-jun Wang,2, Ben-hong Wang, Yuan Tang, Hao-ru Zhao

1. College of Water Resources and Civil Engineering, China Agricultural University, Beijing 100083, China

2. Beijing Engineering Research Center of Safety and Energy Saving Technology for Water Supply Network System, Beijing 100083, China

Abstract: A novel Omega (Ω)-driven dynamic partially-averaged Navier-Stokes (PANS) model is proposed in this paper. The ratio of the modeled-to-total turbulent kinetic energies fk is dynamically adjusted by the rigid vorticity ratio (the ratio of the rigid vorticity to the total vorticity), the key parameter of the Ω vortex identification method. Three classical flow cases with rotation and curvature are used to test the model. The results show that the turbulent viscosity is effectively adjusted by the new dynamic fk and the LES-like mode is activated, which can help the revelation of more turbulence information and improve the prediction accuracy. The new PANS model does not contain any explicit dependency on the grid size and enjoys good adaptability to the flow fields, and can be used for efficient engineering computations of the turbulent flows in the hydraulic machinery.

Key words: Dynamic partially-averaged Navier-Stokes (PANS), turbulence model, Omega, engineering computations

Introduction

The partially-averaged Navier-Stokes (PANS)model was proposed by Girimaji et al.[1]as a second generation URANS approach to resolve the substantial part of the turbulent structures. For high Reynolds number flows, the PANS model can switch from the URANS mode to the LES-like mode where the ratio of the modeled-to-total turbulent kinetic energies fkis reduced yielding a lower turbulent viscosity with high fluctuations[2-3], and it is also easy to be implanted into the existing URANS solver.

The original PANS model is developed assuming that fktakes a fixed value, and it is extensively used in many turbulent separation flow cases, such as the flow over a backward facing step[4], the flow past a square or circular cylinder[5-6], the cavitating flow around a hydrofoil[7], and the swirling flows in the pumps and turbines[8-9]. However, to remedy the assumption of the constant fk, the PANS model is gradually extended to the cases where fkis varied,to promote the development of dynamic methods. For example, Elmiligui et al.[10]proposed a dynamic expression of fk, which is similar in form to the damping function in the near wall region. Girimaji and Abdol-Hamid[11]derived a variable fkaccording to the classical Kolmogorov turbulence theory. Foroutan and Yavuzkurt[12]determined a modified formula of fk, which is inspired from the Von Kármán like energy spectrum equation[13]. Luo et al.[14]used a blending function to reduce the grid influence of the fk-limiter on the URANS computation in the boundary layer. All of these dynamic methods are related to the grid size Δ and the Taylor turbulence length scale λ, and have been successfully used in simulating the unsteady eddying motions[3].

However, as Wilcox said, “an ideal model should introduce the minimum amount of complexity while capturing the essence of the relevant physics”[15]. The current dynamic PANS models do not contain such an explicit dependency on the computation grids like the LES or DES models, but the space scale of the grids Δ is still required for calculating the function fk,which may serve as additional requirements on the grid conditions and affect the efficiency and robustness of engineering computations[16]. Accordingly, it may be a good idea that fkis dynamically adjusted using the flow parameters that directly reflect the features of the turbulent vortical structures,without containing any explicit dependency on the grid size and with the adaptability of fkto the flow field. As an important inspiration, Liu et al.[17]proposed an adaptive k-ω model using the Truesdell’s kinematic vorticity number Nkfor the corner separation flow, which can distinguish the local rotation and the deformation of the fluids. This idea is shown to be feasible. A self-consistent Omega ()Ω vortex identification method was proposed by Liu et al.[18], the key parameter of which is the ratio of the rigid vorticity to the total vorticity. This parameter is also known as the “eddy concentration” and can effectively detect the local features of the turbulent structures[19-20]. Besides, it is normalized and Galilean invariant[21], and is more suitable for the construction of a dynamic expression of fk.

In this paper, a novel Ω-driven dynamic PANS model is proposed, and the ratio of the modeled-to-total turbulent kinetic energies fkis dynamically adjusted by the above-mentioned key parameter of the Ω method. Three classical flow cases, the Taylor-Couette flow, the turbulent swirling flow through an abrupt axisymmetric expansion and the flow in a centrifugal impeller, are used to test this model.

1. Mathematical formulation

1.1 Principle of the Ω method

The Ω method proposed by Liu et al.[18]is originated from the vorticity dualistic decomposition theory[22]. It is indicated that the total vorticity can be decomposed into the rigid vorticity and the deformational vorticity, as expressed as

where ω is the total vorticity,Rω is the rigid vorticity andDω is the deformational vorticity.Moreover, the ratio of the rigid vorticity to the total vorticity Rpcan be given by R∈,. The pure deformation is more appropriately defined as the flows with =0

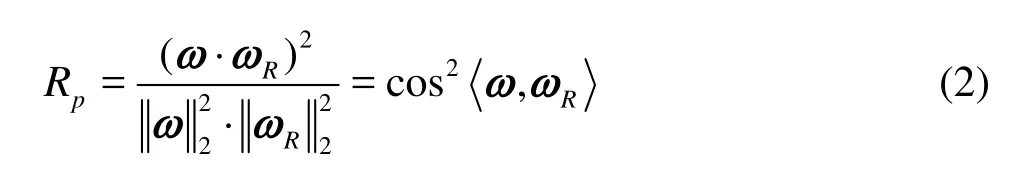
It is obvious that [01]

p

R,

p while the rigid rotation is more appropriately defined as the flows with =1R since the total vorticity is aligned with the vortex axis. In practical applications,the rigid vorticity ratio Rpis expressed as

p

1.2 Constructuion of the new model

The PANS model can be directly derived from a baseline URANS model by introducing the modeled-to-total ratio of the turbulent kinetic energies(fk) and that of the dissipation rates (fε). If there is a clear separation between the energy-containing scale and the dissipation scale (high Reynolds number flow),fεis approximately equal to 1. In this paper, the classical RNG k-ε model with the Spalart-Shur correction[23]is employed as the baseline URANS model. According to the conditions of km=fkk and εm≈ε, the transport equations of the modeled turbulent kinetic energy （km)and the dissipation rate（εm) are expressed as

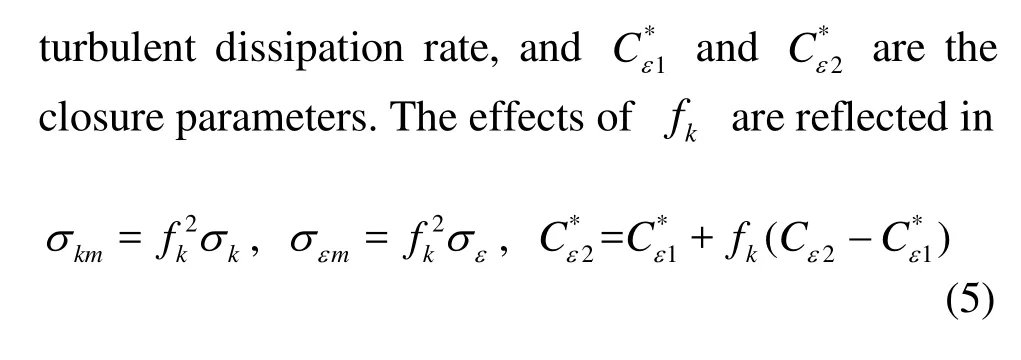
wherekσ is the original Prandtl number of the turbulent kinetic energy,εσ is the original Prandtl number of the turbulent dissipation rate and C2εis the original closure constant.

In order to derive the Ω-driven dynamic fk, it is necessary to clarify the relationship between the local features of the turbulent structures and the resolving ability of the turbulence model. According to the relevant researches, if the local fluids are in a strong rotation state ( Rp→ 1.0, e.g., in the vortex core region), the helical features induced by the rotatingcansuppressthe direct cascadeprocess and decreasetheturbulentviscosity[24].Ifthelocalfluids are in a strong deformation state ( Rp→ 0, e.g., in the free shear layers and the vortex boundary region), the effects of the energy dissipation and the eddy maintenancecausedbythe strongshearing also help therevelationof theturbulenceinformation[25].And if the local fluids are in a relative equilibrium state( Rp→ 0.5, e.g., in the viscous sublayer), the hybrid mode activated by the PANS model should be degenerated to the URANS mode. Accordingly, the Rp-based dynamic fkcan be expressed as

where Rpis the rigid vorticity ratio, α, β and γ are empirical coefficients. To well reflect the above“relationship”, based on the previous researches for the fixed fk, the values of α, β and γ are chosen as -1.6, 1.2 and 0.6, respectively. It implies that the lowest fkis 0.2 while the average fkis approximately 0.67, and the resolving ability of the PANS model might be effectively ensured. Moreover,three classical high Reynolds number flow cases, the Taylor-Couette flow, the turbulent swirling flow through an abrupt axisymmetric expansion and the flow in a centrifugal impeller, are used to test this model.

2. Applications of the new model

2.1 Taylor-Couette flow

The Taylor-Couette flow is one of the paradigmatic systems of the physics of the fluids, and is the flow between two coaxial and independently rotating cylinders[26]. It is a good test case for verification and validation of the turbulence model used for the turbulent flows with rotation and curvature. According to the previous simulations of this flow case[27-28], the computational domain and the meshing results are determined, as shown in Fig. 1.The inner cylinder rotates at a constant angular velocity, while the outer cylinder is in the stationary state. The Reynolds number based on the inner radius 1R, the outer radius2R and the circumferential velocity of the inner wall Uθis 8 000, and the Taylor number is 6.4×107. Hexahedral grids are adopted to discretize the domain, and the mesh is comprised of 128×32×64 elements in the circumferential, radial and axial directions. Periodic conditions are imposed in the axial direction, and the no-slip conditions are applied on- the cylinder surfaces.

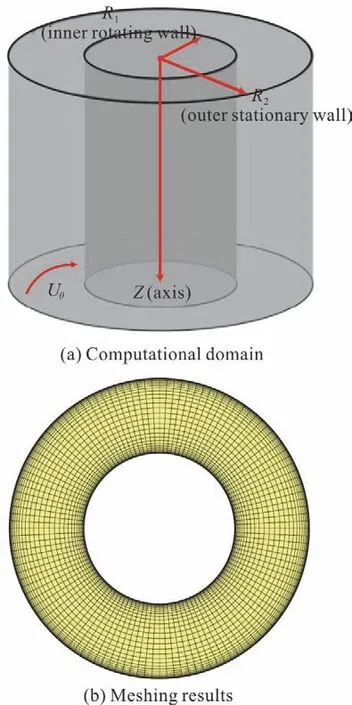
Fig. 1 (Color online) Computational domain and meshing results of Taylor-Couette flow

The distributions of the mean circumferential velocity and the turbulent vortical structures are shown in Fig. 2, and the turbulent vortices are visualized by the iso-surfaces of the Liutex criterion parameter[29]. The Liutex is a new physical quantity in scalar, vector and tensor forms to exactly represent the rigid-body angular speed of the local fluids[30-31].

Compared with the DNS results[27], the new Ωdriven PANS model gives a reasonably accurate prediction results (Fig. 2(a)). And compared with the URANS results[32], more detailed turbulent vortices are captured by the new model (Fig. 2(b)).Accordingly, the new model with an adaptive dynamic fkdoes ensure the prediction accuracy, and the novel idea can be applied.

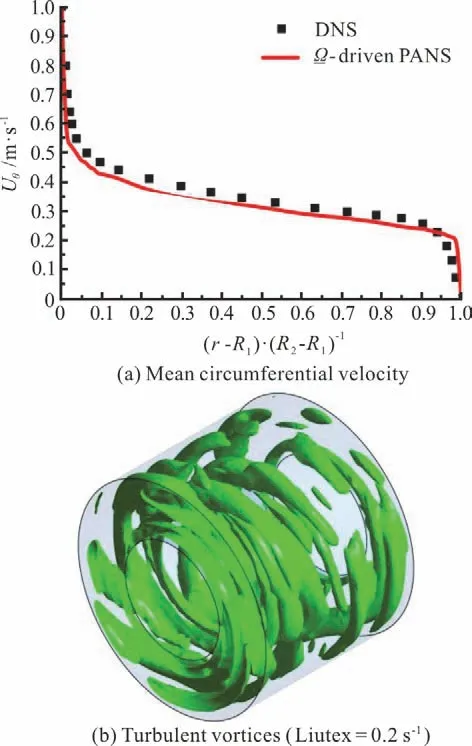
Fig. 2 (Color online) Distribution of mean circumferential velocity and turbulent vortical structures

2.2 Swirling flow through an abrupt axisymmetric expansion

The turbulent swirling flow through an abrupt axisymmetric expansion is a complex flow case involving many dynamic phenomena such as the vortex breakdown, the detachment and the reattachment[12]. It is also a good test case for verification and validation of the turbulence model used for the turbulent flows with rotation and curvature. According to the previous simulations of this flow case[12,33], the computational domain and the meshing results are determined, as shown in Fig. 3.The Reynolds number based on the inlet diameter D0and the bulk velocity U0is approximately 3×104,and the swirling number Sris approximately equal to 0.6. High quality hexahedral grids are adopted to discretize the domain, and the total number of grids is approximately 1.66×106. The velocity inlet condition with a high turbulence intensity is used according to the experimental data[34]. The pressure outlet condition and the no-slip wall condition are adopted.

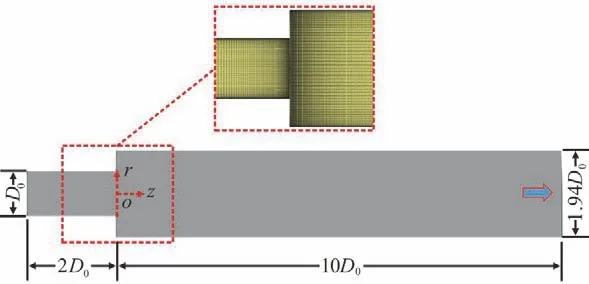
Fig. 3 (Color online) Computational domain and meshing results of the swirling flow

The distributions of the mean axial velocity Uzand the circumferential velocity Uθon three cross sections behind the expansion, corresponding to z/ D0=0. 25-0. 75, are shown in Fig. 4. Compared with the experimental results and other simulations[12,33-34],the new Ω-driven PANS model gives a reasonably accurate prediction results. Moreover, the distributions of the power spectrum density (PSD) and the turbulent vortical structures are shown in Fig. 5, and the turbulent vortices are visualized by the iso-surfaces of the Liutex criterion parameter[29]. Obviously, the resolved scales are asymptotic to the inertial subrange(the classical -5/3 scaling), which indicates that the LES-like mode is activated. Moreover, the important phenomenon, “a precessing vortex core rotates around the geometrical axis and subsequently breaks down to small coherent structures”[12], is also captured by the new model.

2.3 Flow in a centrifugal impeller

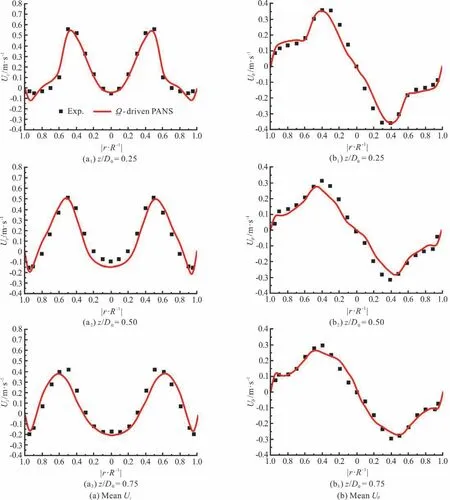
Fig. 4 (Color online) Distributions of mean axial and circumferential velocity

The distributions of the relative radial velocity Vr/V2and the circumferential velocity Vθ/V2(streamwise r/R2=0.5 ) are shown in Fig. 7.Compared with theexperimentalresultsandother simulations[35-36],thenewΩ-driven PANSmodel gives a reasonably accurate prediction results. The iso-surfaces of the turbulent vortical structures colored by the viscosity ratio μt/μ are shown in Fig. 8. The turbulent viscosity and the dynamic viscosity are at most of the same order of magnitude, which is much smaller than the computation results of ordinary URNS models. Accordingly, the turbulent viscosity is effectively adjusted by the new dynamic fk, which can help the revelation of more turbulent information.

3. Summary and conclusions

A novel -Ωdriven dynamic PANS model is proposed in this paper, and the ratio of the modeled-to-total turbulent kinetic energies fkis dynamically adjusted by the key parameter Rp(the rigid vorticity ratio) of the Ω vortex identification method (proposed by Prof. Chaoqun Liu), the idea of which is inspired from the relationship between the local features of the turbulent structures and the resolving ability of the turbulence model.

Fig. 5 (Color online) Distributions of power spectrum densityand turbulent vortical structures

Fig. 6 (Color online) Computational domain and meshing results of the centrifugal impeller

Through the tests of three classical high Reynolds number flow cases with rotation and curvature, the Taylor-Couette flow, the turbulent swirling flow through an abrupt axisymmetric expansion and the flow in a centrifugal impeller, it is found that the turbulent viscosity is effectively adjusted by the new dynamic fkand the resolved scales are asymptotic to the inertial subrange (the LES-like mode), which can improve the prediction accuracy and capture more turbulent vortices.

The new model does not contain any explicit dependency on the grid size Δ and possesses a good adaptability to the flow fields, and can be used for engineering computations of turbulent flows in hydraulic machineries.

Fig. 7 (Color online) Distributions of relative radial and circumferential velocity at r/R2=0.5

Fig. 8 (Color online) Iso-surfaces of vortical structures colored by viscosity ratio (Liutex=200s-1)