振动态在抽运探测激光驱动下对谐波辐射强度的影响

李 义，冯立强,2

(1. 辽宁工业大学理学院，锦州 121001；2. 中国科学院大连化学物理研究所 分子反应动力学国家重点实验室，大连 116023)

1 引 言

经过近三十年的研究，强场物理领域已经有了很大的发展. 其中，高次谐波作为强场物理以及非线性光学领域的重要现象得到了广泛的关注[1-2].

高次谐波可以由强激光场驱动原子、分子、等离子体以及固体来获得[3-4]. 其中，激光驱动原子、分子辐射高次谐波作为获得阿秒量级超短光源的方法更是被广泛研究. 目前，激光驱动原子、分子辐射高次谐波的过程可由半经典的三步模型[5]来解释. 具体来说：首先, 电子在激光驱动下由隧道电离进入连续态；其次，自由电子在后续激光驱动下加速并获得能量；随后，在激光反向驱动下，电子有几率与原母核发生碰撞，进而辐射出光子能量为基频场倍数的高阶谐波. 当然，如果辐射谐波相位匹配，通过叠加谐波平台的谐波可获得阿秒量级的超短光源.

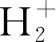
2 计算方法

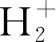
(1)

(2)

其中，mp为H核质量；R和z为核与电子坐标. 激光场E(t)可表示为：

E(t)=E1f1(t)cos(ω1(t-tdelay))+

E2f2(t)cos(ω2t)

(3)

其中，Ei、ωi和fi(t) (i = 1, 2)分别为激光场的振幅、频率和激光包络. tdelay为2束激光延迟时间. 脉冲包络fi(t)是10个光学周期的梯形形状，其中包含2个周期的激光上升和下降区间以及6个周期的激光振幅区间(标记为2-6-2 laser). 抽运激光和探测激光的激光波长都为λ=800 nm. 抽运激光和探测激光的强度分别为I1= 0.5×1014W/cm2和I2=1.0×1014W/cm2.

高次谐波谱图可表示为：

(4)

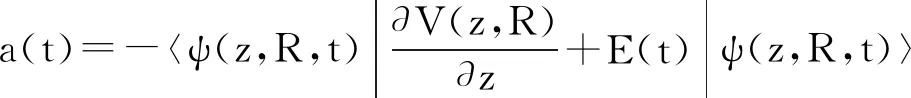
3 结果与讨论

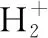
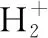
减小，如图1(b)所示，并且谐波辐射强度与υ=0时相比有明显增强. 当振动态继续升高时(例如：υ=4)，较大延迟时间下的谐波辐射强度(例如：tdelay= 3.0 T)反而高于较小延迟时间下的谐波辐射强度(例如：tdelay= 0)，如图1(c)所示. 这里T表示800 nm激光场的光学周期.

为了解释谐波辐射强度的变化，图2和图3给出了上述激光包络图以及谐波辐射的时频分析图[16]. 首先低振动态下(例如：υ=0，见图2所示)延迟时间为tdelay=0；tdelay= 2.0 T和tdelay= 3.0 T. 当谐波阶数大于35阶时，谐波光谱的主要贡献分别来自于t=4 T到t=6.5 T (相对于tdelay= 0情况)； t=4 T到t=6 T (相对于tdelay=2.0 T情况)；以及t= 5 T到t= 6.5 T (相对于tdelay= 3.0 T情况)，如图2(b)，2(d)和2(f)白色框线区域所示. 由图2可知，高强度谐波辐射主要来源于激光下降区间，即，t> 8.0 T. 对于谐波辐射在t= 4 T到t= 6.5 T区间，其辐射强度随着延迟时间增大而减弱，这是导致图1(a)中谐波辐射强度随抽运探测激光延迟时间增大而减小的原因.

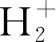
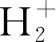
图2 激光包络图以及υ=0时谐波辐射时频分析图：(a)～(b) tdelay= 0；(c)～(d) tdelay=2.0 T；(e)～(f)tdelay= 3.0 T

Fig.2 The laser profiles and the time-frequency analyses of the harmonics from v = 0: (a)～(b) tdelay= 0; (c)～(d) tdelay= 2.0 T; (e)～(f) tdelay= 3.0 T

图3 υ=2和υ=4时谐波辐射时频分析图: (a)和(d) tdelay= 0；(b)和(e) tdelay= 2.0 T；(c)和(f) tdelay= 3.0 T

Fig.3 The time-frequency analyses of the harmonics from v = 2 and v = 4: (a) and (d) tdelay= 0; (b) and (e) tdelay= 2.0 T; (c) and (f) tdelay= 3.0 T

4 结 论