深水水下夹层管非线性屈曲特性*

黎之奇， 詹 玮

(湖南大学 土木工程学院， 长沙 410082)

随着海上油气开采逐步向深海推进，原来的单层油气输送管逐步发展为夹层管.夹层管由三层独立的管道组成，即内层、外层钢管以及由填充在两管环形空间的轻质保温绝热材料组成的夹芯层，三层式的结构形式使其在满足刚度要求的同时，夹层材料起到了隔热和保温作用，防止在深海环境下油气输送过程中突然降温而导致的堵塞.

随着夹层管的应用，国内外学者对于夹层管在各种荷载组合下的屈曲失稳进行了一系列研究.目前的理论分析主要基于以最小势能原理和数值计算相结合的方法，并考虑了失稳过程的变形非线性及各管之间的粘结情况[1-10].由于理论解未考虑在失稳前各层材料的屈服及塑性发展，因此，与试验结果比较会产生较大的误差，而通过建立夹层管的有限元模型进行夹层管在各种荷载下的极限承载力分析是目前较为有效的方法.Arjomandi和Taheri[11-12]基于材料弹性假设和弹塑性假设，运用Abaqus软件研究了夹层管在外压作用下的稳定性和后屈曲特性.通过大量的有限元模型研究了各种不同的结构参数，如厚径比、材料的相对弹性模量以及初始椭圆度等对夹层管临界屈曲压力的影响.通过进一步分别设定内外管与中间层的不同层间条件，重点分析了层间关系对承压能力的影响.Hashemian和Mohareb[13-14]将特征值法应用于夹层管的有限元计算.An等[15]提出了将钢纤维及PVA增强水泥基材料作为夹层管的填充材料，通过压力舱试验对夹层管在外压下的极限强度进行了研究.国内研究人员运用有限元软件Abaqus建立在不同载荷作用下夹层管的计算模型，讨论了结构参数以及夹芯层与内外管不同粘结方式对夹层管屈曲压力与特征路径的影响机理[16-18].

夹层管中间层材料的主要作用是保温，同时起到一定的承载作用.现有的夹层管中多采用聚合物材料作为夹芯层.文献[19]提出将固体聚丙烯、纯水泥和纤维增强应变硬化水泥等作为夹芯层.目前，对于这种具有非线性中间层材料的夹层管还缺少对其影响因素进行系统分析的研究成果.由于求解夹层管的真实结构响应存在很多的非线性因素，包括材料非线性、几何非线性和层间条件等，使用非线性有限元法会得到更加准确的结果.本文针对以纤维增强应变硬化水泥基复合材料作为中间层的夹层管，通过非线性有限元分析的方法建立计算模型，对夹层管在外压作用下的屈曲特性和极限承载力进行计算，重点考察层间粘附条件、内外管厚径比等参数的影响，并与试验结果进行了比较，其结果对深水水下夹层管设计具有一定指导意义.

1 夹层管非线性屈曲有限元计算模型

夹层管由外层钢管、中间夹层和内层钢管组成，结构如图1所示.内层管为油气输送层，中间夹层为保温层，外层管将内部各层与周围的海水环境隔离.

图1 夹层管结构示意图Fig.1 Schematic structure of sandwich pipe

深海海底油气输送管道长度可达数千米，因此，可认为管道中所有的几何性质、荷载与边界条件均沿管道长度方向均匀分布，将问题简化为二维平面应变问题.模型单元类型选用8节点线性缩减积分单元，内、外管沿径向分别划分为1个单元，夹芯层沿径向划分为8个单元，内外管和夹芯层沿环向均分为160个单元，因屈曲分析简化为平面应变问题，沿管道轴向可划分为1个单元，可以得到足够精确的结果.

对于夹层管，按其制造工艺和夹层材料，夹层与钢管之间可分为完全粘结、部分粘结和完全不粘结三类，其中，部分粘结方式情况复杂，屈曲荷载则介于完全粘结和完全不粘结形式之间.由于层间粘结情况对于极限承载力有很大的影响，完全粘结与完全不粘结则决定了夹层管的最大和最小曲屈荷载.因此，本文计算了“完全粘结”和“完全不粘结”两种层间关系.两种层间关系都通过定义接触面的相互作用来实现，接触界面由法向接触压力模型和切线方向的库伦摩擦模型确定.对于“完全不粘结”条件，接触面彼此允许发生法向和切向相对移动，接触面正切方向无摩擦建模.对于“完全粘结”条件，接触面不允许发生相对移动，切向定义罚函数，并取摩擦系数为1，同时设定极限剪强度为无穷大.

有限元计算模型的单元划分及施加的荷载和边界条件如图2所示.均布外压施加在外管的外表面上，使用自动生成的运动学耦合方程将横向平面节点的自由度与参考点耦合，约束Z方向的运动，其他五个自由度保持自由移动以模拟长管结构的平面应变状态，另一横截面上设置Z向对称约束，从而避免过约束问题.

夹层管屈曲失稳表现为材料非线性和几何非线性，因此，数值模型的计算分析需要增加几何非线性计算选项(Nlgeom).考虑到夹层管屈曲变形随外压增加而逐渐增大，在曲屈荷载附近，较小的外压增量也会引起较大的变形，所以选择弧长法(Riks)进行计算，并采用自动增量控制.

图2 夹层管有限元模型Fig.2 Finite element model for sandwich pipe

2 模型验证

(1)

式中：ε为真实应变；σ为真实应力；σy为屈服应力；E为杨氏模量；n为材料硬化系数.材料塑性特性采用各项同性强化J2塑性流动理论计算.

表1 内外层钢管材料参数Tab.1 Material parameters for inner and outer steel pipes

夹层材料为纤维增强应变硬化水泥基复合材料，采用Abaqus材料库中的CDP(混凝土塑性损伤)模型来定义其弹性、塑性和损伤行为[20].对于应变硬化水泥基材料，依据文献[21]取泊松比为0.2，膨胀角为24.7°，同时，根据文献[22]定义粘性参数μ=0.001，用来改善混凝土软化和刚度退化状态下的收敛速度.

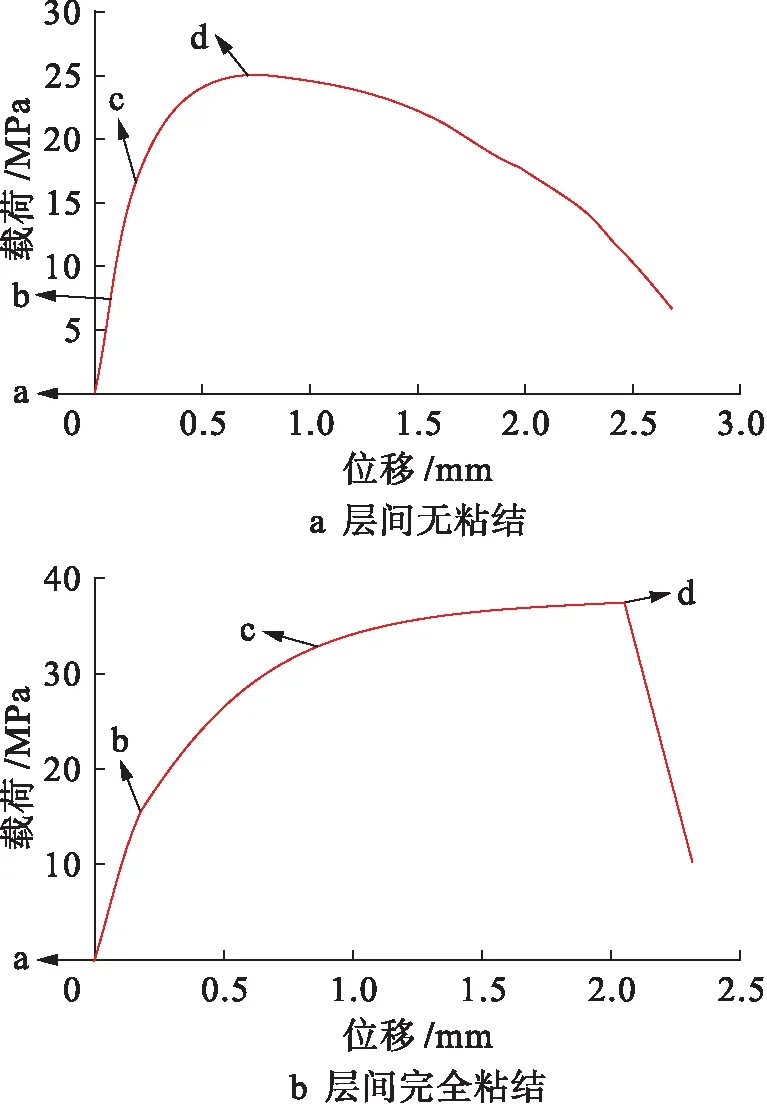
图3 夹层管在外压作用下的载荷位移曲线Fig.3 Load-displacement curve of sandwich pipe under external pressure

从图3中可以看出，载荷曲线先上升后下降，在图中存在一载荷最大值，在该点时，夹层管结构发生屈曲，载荷值即为临界屈曲外压.从图4、5可以看出，夹层管在达到压溃压力之前有较大的塑性变形过程，并且在屈曲发生时，层间完全粘结情况下的塑形应变高于层间无粘结的情况.对于层间粘结和不粘结两种情况，夹层管结构的塑性应变都首先出现在内层钢管，并且随着外压的增加，塑性应变区逐渐扩展至夹层以及外层钢管，当达到临界屈曲荷载时，各层塑性应变分布如图4d、5d所示，内层钢管及中间水泥基夹层材料均出现塑性变形，在管道对称纵截面处出现较高的塑性应变.两种层间粘结条件下的计算结果及与试验的比较如表2所示.

结果表明，试验值处于完全不粘结和完全粘结两种计算值之间，与实际夹芯层与内外管之间的粘结性介于完全粘结与完全不粘结之间的结论一致，验证了本文采用的有限元模型的适用性和正确性.

图4 层间无粘结夹层管的塑性应变分布Fig.4 Plastic strain distribution of sandwich pipe

3 影响参数分析

3.1 参数范围

夹层管的曲屈外压与各几何材料参数相关，

图5 层间完全粘结夹层管的塑性应变分布Fig.5 Plastic strain distribution of sandwich pipe under fully-bonded interlayer condition

其无量纲函数关系式为

(2)

式中：Pcr为夹层管的曲屈外压；Ep和Ec分别为内外钢管和夹芯层的弹性模量；Δ0为夹层管结构的初始椭圆率，其作用相当于初始扰动；vc和vp分别为夹芯层和内外管的泊松比；t1、r1和t2、r2分别为外管和内管的厚度与外半径.vc、vp取值分别为0.2、0.3，Ep取值为200 GPa.实际管件在制造过程中由于工艺原因都有一定的初始椭圆率.研究表明，初始椭圆率在0.1%～1.5%范围内对夹层管的曲屈荷载影响很小[11-12]，依据An等人的试验，本文计算初始椭圆率均取为0.2%.钢管厚径比t/r的取值范围为0.03～0.09，这一范围能够涵盖绝大部分API 5L标准厚度管道的厚径比.表3为算例的参数取值.

表2 夹层管压溃压力计算与试验结果的比较Tab.2 Comparison between experimental and calculated results of collapse pressure of sandwich pipe

注：Pco为夹层管压溃压力.

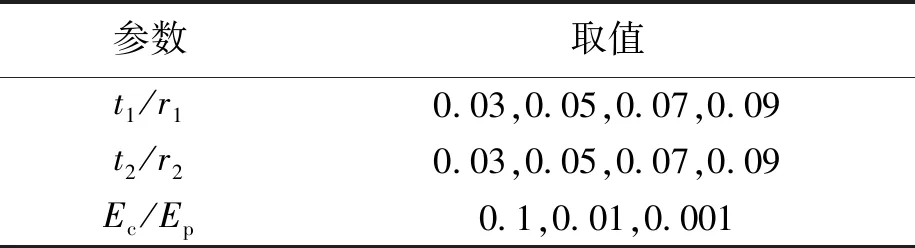
表3 算例的参数取值Tab.3 Parameter values of calculation examples

夹层管在外压作用下的变形特征响应由外管的椭圆率表示，即

(3)

(4)

3.2 层间粘结条件影响

图6 不同层间粘结的夹层管在外压下的特征响应

Fig.6 Characteristic response of sandwich pipe under external pressure and different bonded interlayer conditions

3.3 内外管厚径比影响

内管和外管取不同厚径比t/r时(初始椭圆率Δ0=0.2%)，对完全粘结和无粘结两种情形下夹层管承载力的影响计算结果如图7所示，其中，实线表示外管厚径比t1/r1=0.05时改变内管厚径比的结果，虚线为内管厚径比t2/r2=0.05时改变外管厚径比的结果.结果表明：1)外管厚径比和内管厚径比的增大都可以提高夹层管的承压能力，层间完全粘结时，提高内管的厚径比对夹层管的整体承载力影响更明显；2)层间不粘结时，二者对夹层管的整体承载力影响接近.由于增加内管的厚径比对夹层管的重量影响较小，因此从经济性上考虑更合理.

3.4 夹芯层材料弹性模量影响

图7 内外管厚径比对夹层管屈曲压力的影响

Fig.7 Influence of different thickness-to-diameter ratios of inner and outer pipes on buckling pressure of sandwich pipe

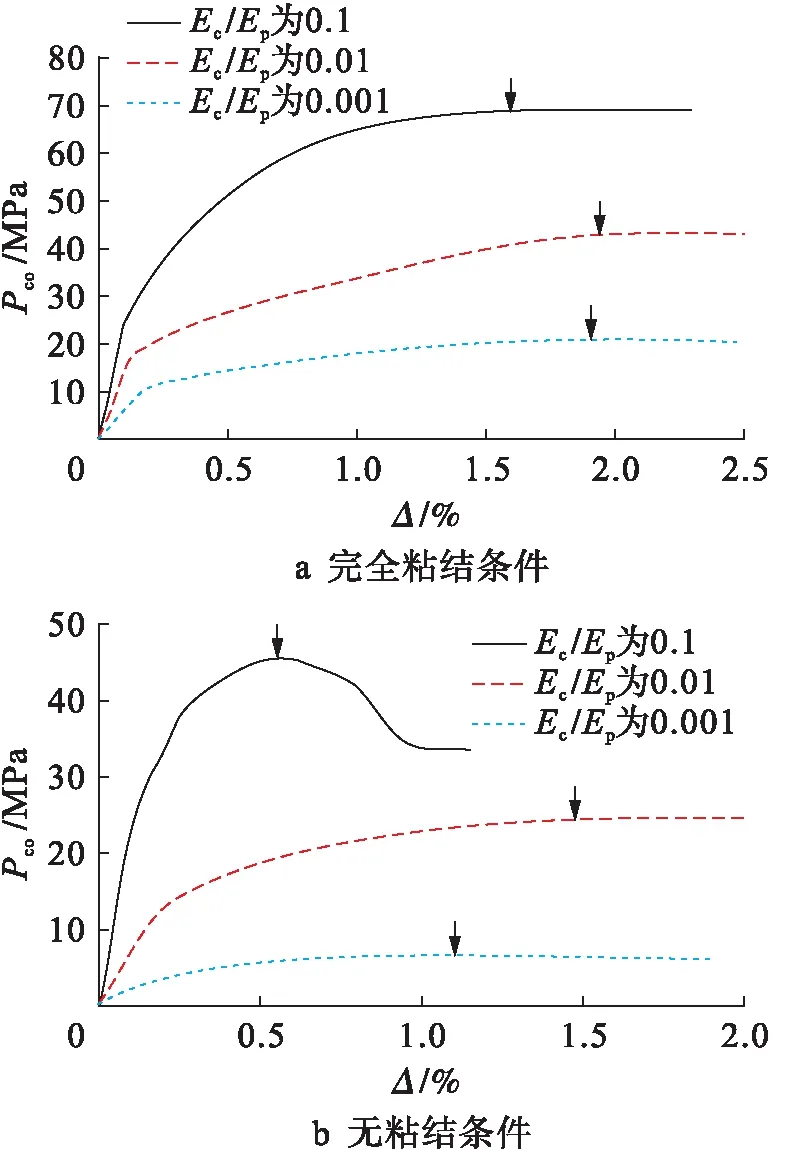
图8 不同夹芯层弹性模量的夹层管在外压下的特征响应

Fig.8 Characteristic response of sandwich pipe with core material of different elastic modulus under external pressure

在两种粘结情况下，夹层管的压溃压力随夹芯层材料弹性模量增加而增大，因此，选择夹芯层材料时，在满足一定的保温性能要求下应选用弹性模量较高的材料以提高其结构性能.

4 结 论

本文通过分析得出以下结假定格栅式地下连续墙为弹塑性材料论：

1) 夹层管受外压作用时，内管首先出现塑性应变，随着荷载的增加，中间层也出现塑性应变，直至荷载达到临界压力时管道发生压溃破坏.

2) 层间剪应力对夹层管的承载力有重要影响，在层间完全粘结的情况下，夹层管的承载力得到明显提高，并且在压溃前的塑性变形也明显增加.

3) 夹层管结构的各层几何比例对于其极限承压能力有较大影响.增加内管或外管的厚径比均可以提高夹层管的极限承压能力，在层间完全粘结时，内管厚径比的增大对夹层管压溃压力的影响更明显.

4) 夹层材料特性对夹层管屈曲失稳性能有较大影响，在满足保温性能设计的前提下，应尽量采用高弹性模量材料作为夹层材料.