显热蓄热式电暖器供暖室内温度场的实验研究

高晨晖，张兴惠，马质聪，王少博

(太原理工大学 土木工程学院，太原 030024)

2018年7月，国家发展改革委印发《关于创新和完善促进绿色发展价格机制的意见》[1]，明确提出要充分发挥电价的杠杆作用，优化资源配置，促进产业升级，节能减排。在此基础上，各省相继出台峰谷电价的配套政策，鼓励用户利用储能削峰填谷。

蓄热式电暖器能在电价低谷时将热量蓄存，全天逐渐释放，具有清洁、舒适、节能、卫生、性价比高等优点，不仅在我国北方地区，而且在长江流域夏热冬冷地区，也能有效地改善居室内热环境[2]，节约资源，受到越来越多人的青睐[3-4]。刘靖等[5-6]设计了一种相变蓄热电暖器，但其蓄热密度欠缺；BROUSSEAU et al[7]提出了多层相变蓄热系统，用于平衡电负荷；马贵阳等[8]改进了蓄热材料，强化了内部传热；MAWIRE et al[9-11]针对蓄热系统建立了仿真试验，评价了不同蓄热材料的性能；张斌[12]对已投入使用的蓄热电暖器供暖系统进行测试，评估其能耗和费用；廖晋[13]建模分析了材料和介质的温度场，得出电暖器的蓄放热特性；梁炬祥[14]从热物理的角度提出了具有应用前景的固体蓄热材料。本研究在人工气候室中搭建了显热蓄热电暖器供暖系统，通过对室内温度场的实验测试，分析蓄热型电暖器在不同室外温度、不同蓄热时间以及不同时刻的散热能力。

1 实验装置

1.1 实验装置

实验在太原理工大学人工气候室中进行，气候室尺寸为3.9 m×2.8 m×3.0 m，围护结构采用双面4.2 mm厚彩钢板，内部填充100 mm厚聚氨酯板，传热系数为0.25 W/(m2·℃).窗为普通玻璃推拉窗，传热系数为3.3 W/(m2·℃).人工气候室置于地下一层的实验室内，实验期间外部实验室的温度由热电阻实时测量记录。

实验装置选用显热式蓄热电暖器AZDX1600，额定功率1 600 W，额定蓄热量12.0 kW·h.内置加热元件为英格莱840合金钢，蓄热材料为高密度微晶陶瓷蓄热材料，最高工作温度可达750 ℃.蓄热电暖器尺寸为590 mm×620 mm×200 mm，置于气候室一侧中央，距墙500 mm，电暖器距地550 mm位置处有栅状出风口，热空气在热压驱动下从风口吹出。电暖器由CX-TGK01G微电脑时间控制自动启停。电暖器加热元件与蓄热材料见图1.

图1 电暖器加热元件与蓄热材料Fig.1 Electric heater heating element and heat storage material

1.2 测点布置

温度测试所用传感器为A级Pt100铂电阻，测温范围为-50～450 ℃，精度为(0.15±0.002×|t|)℃，t为实际温度。在蓄热电暖器正表面布置三个热电阻，在气候室外的实验室中布置三个热电阻，分别测量电暖器表面和气候室外部空气温度，气候室实景图见图2.气候室内测点的选取基于ISO 7730中对房间舒适性的规定。针对人体不同部位的温度需求，兼顾测点对区域温度评价的均匀性，沿竖直方向分别在离地面400 mm、1 200 mm、2 000 mm处布置三层热电阻，每层四行四纵，共48个点位，如图3所示。气候室外的测点以W1、W2、W3编号，电暖器表面测点以O1、O2、O3编号，气候室内测点分ABCD四行，第一行第一列自上而下的三个测点分别编号A11、A12、A13，以此类推[15-17]。

图2 气候室实景图Fig.2 Climate room real map

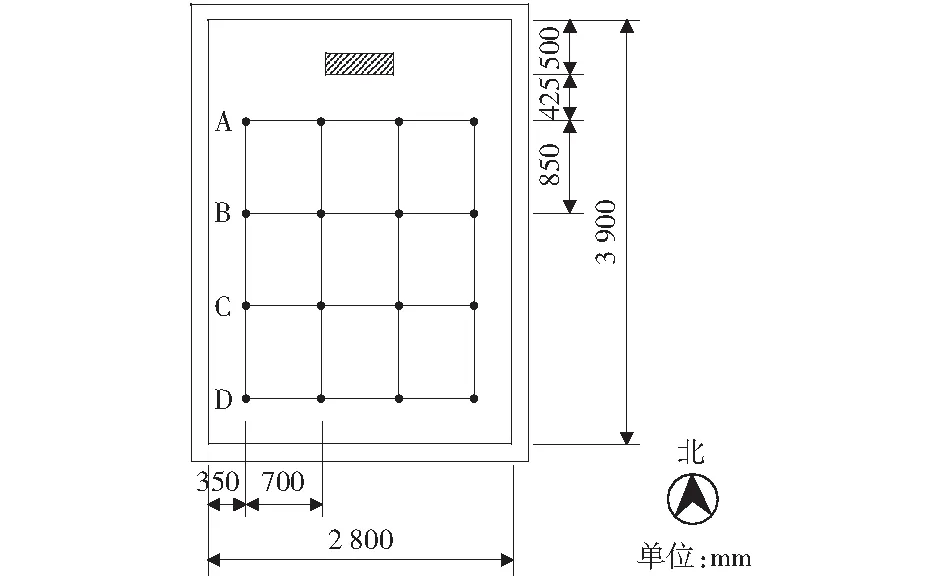
图3 测点布置示意Fig.3 Point arrangement

1.3 数据采集仪

实验采用SWP-ASR-MD智能化64路巡检仪自动检测和记录数据，测试精度为0.5%FS±1字，巡检仪对每路信号的采样时间为0.5 s，数据记录时间间隔为300 s.巡检仪与PC机连接，采集到的信号实时传到电脑上。

2 实验方案

通过调节实验室外窗和散热器开闭状态，改变气候室外部区域空气温度；通过设置蓄热电暖器自动启停时间，改变其蓄热时间，蓄热8 h时，设备在22:00开启，次日6:00关闭，蓄热9h时，设备在22:00开启，次日7:00关闭，蓄热10 h时，设备在22:00开启，次日8:00关闭。厂家建议蓄热时间为22:00至次日7:00.在不同工况条件下对气候室温度分布及其规律进行实验研究，实验工况见表1.

3 实验数据处理

3.1 有效性验证

基于SPSS软件，对测试得到的温度数据进行有效性验证。一个完整的实验周期为24 h，数据间隔为300 s时，48个测点共产生数据13 824个，每个测点分别取整点数据值代表其在1 h内的温度情况，一个实验周期内每个测点共有数据24个。将数据分别导入SPSS软件进行统计分析，数据有效性为100%.气候室内部分空气温度测点的数据统计信息见表2.

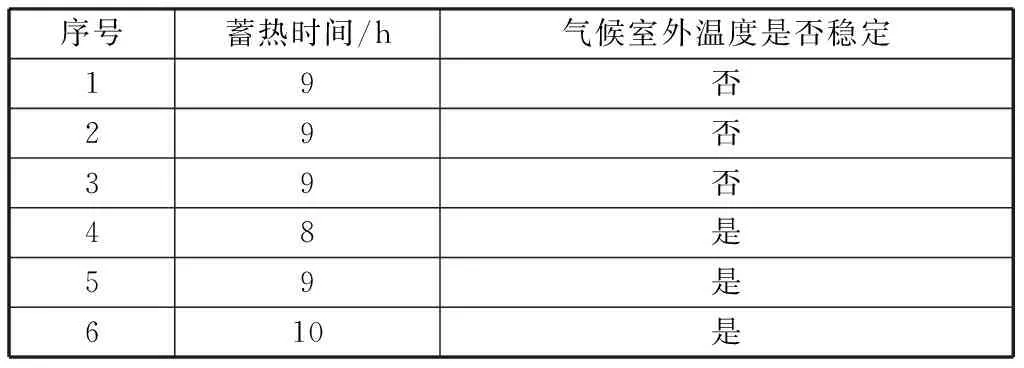
表1 实验工况Table 1 Test condition

3.2 正态分布验证

通过SPSS软件，对数据进行了K-S检验，分析其是否符合正态分布规律[18]。如表3所示，以前5个测点为例，Z值分布在0.5附近，P值(渐近显著性)均大于0.05，结果表明，检验分布为正态分布。同时，在Q-Q图(图4、图5)中，各点拟合直线为y=x，在表2中，偏度系数和峰度系数都小于1，都可以认为数据近似于正态分布。

表2 部分数据统计量Table 2 Partial data statistic

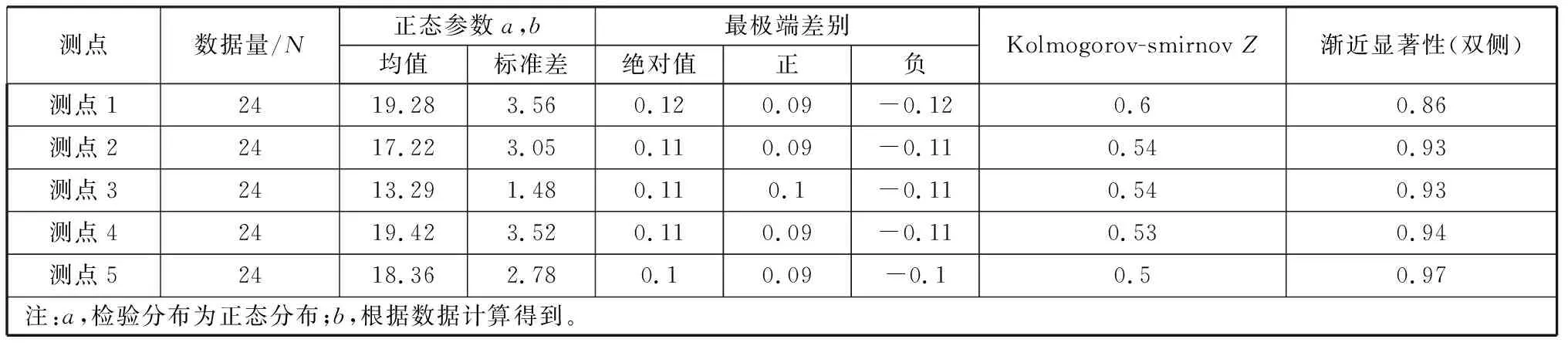
表3 单样本Kolmogorov-Smirnov检验Table 3 Single sample Kolmogorov-Smirnov test

3.3 数据处理方法验证

分别采取算术平均值、加权体积平均值、中位值、稳健平均值的处理方法分析数据[18]。因为气流小室中测点在三个维度上都是均匀分布，其加权体积平均值与算术平均值一致，所以只比较分析算术平均值、中位值、稳健平均值对于反映整体温度状况的优劣性。

3.3.1算术平均值

同一时刻气候室内各测点温度的算术平均值为

(1)

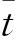
图4 测点1的正态Q-Q图Fig.4 Normal Q-Q diagram of point 1

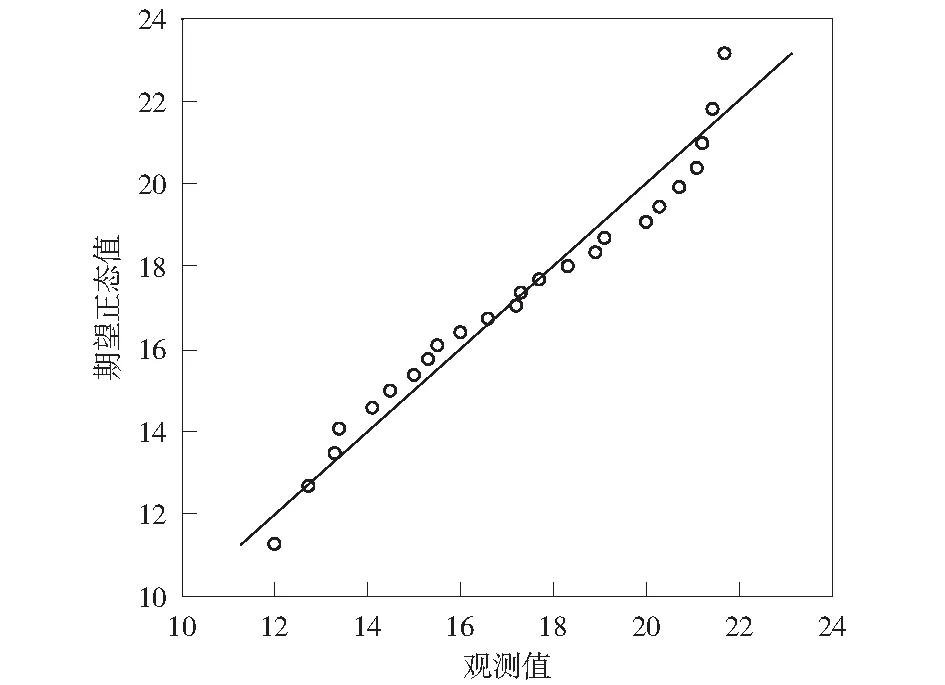
图5 测点2的正态Q-Q图Fig.5 Normal Q-Q diagram of point 2

3.3.2中位值

将同一时刻气候室内各测点温度按照从高到低的顺序排列，取中间位置的温度值作为中位值，即

(2)

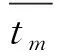
3.3.3稳健平均值

本文采用迭代算法的稳健平均值进行计算，其具体的处理过程分三步进行：

① 计算数据的初始稳健平均值t*和初始稳健标准差s*

t*=medt(i) (i=1,2,…,n) .

(3)

s*=1.483med|t(i)-t*| (i=1,2,…,n) .

(4)

② 更新t*和s*

令φ=1.5s*，对每个t(i)，

(5)

③ 计算新的t*和s*

(6)

(7)

通过迭代计算，重复步骤②③若干次，直到所得t*和s*的估计值变化很小为止。按照此方法对同一时刻气候室内各测点的温度数据进行计算，最终得到稳健平均值。

3.3.4可靠性比较

为了检验3种数据处理方法的可靠性，明确测点布置数量的改变对反映局部区域温度的有效性，在原数据样本中分别增加了5个新的测点，增加的测点温度分别为原样本中温度最大值的50%，75%，100%，125%，150%.利用3种数据处理方法分别对5组新样本进行分析，并将结果与原样本进行比较，从而判断3种方法的可靠性。因数据分布较为集中，几乎不存在极端值，因此稳健平均值的计算结果在数值上与算术平均值一致，所以只需要比较算术平均值和中位值。以2019-01-11 06：00数据为例，见表4.

表4中，平均偏差百分比为5个新样本的计算结果与原样本计算结果的偏差百分比的平均值。从比较结果来看，中位值的平均偏差百分比较低，结合中位值的计算定义可得，该种处理方法能较为准确地反映出部分区域的温度状况。

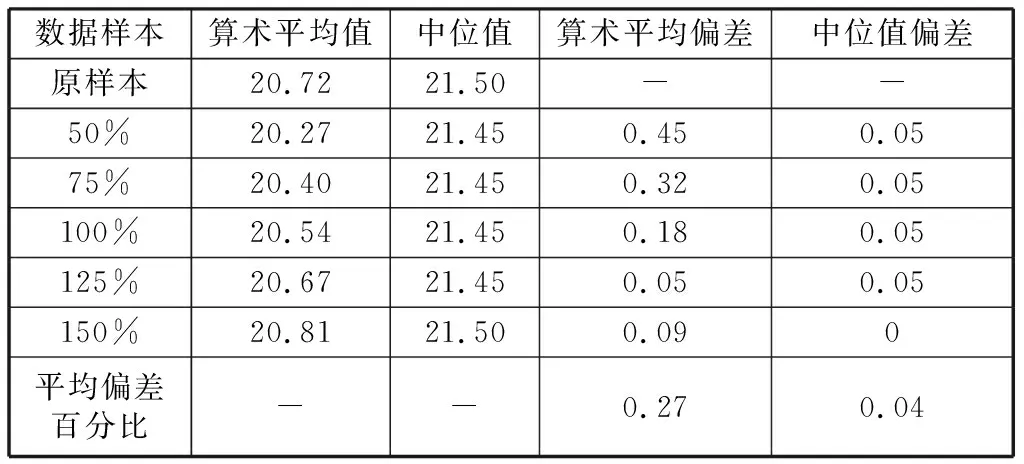
表4 处理结果比较Table 4 Partial data statistic

4 实验结果与分析

4.1 额定蓄热时间下室内温度场随时间和测点位置的变化

当蓄热电暖器蓄热9 h时(晚22:00开启，次日07:00关闭)，室外全天温度为-11～4 ℃，相对湿度18%～57%，风力小于三级。室内纵断面各测点平均温度如图6所示。其中，A断面距电暖器425 mm，B断面距电暖器1 275 mm，C断面距电暖器2 125 mm，D断面距电暖器2 975 mm.

结合图6可以看出：

1) 气候室内平均温度在蓄热阶段迅速上升，到凌晨03:00左右蓄热量逐渐饱和，温升速度减缓，此时电暖器表面温度达到峰值，最高温度为167.2 ℃，平均温度为88.1 ℃，电暖器关闭时，平均表面温度为74.8 ℃，室内平均温度达到最大值，随后，气温随时间缓慢下降，直到电暖器再次启动开始蓄热，此时电暖器平均表面温度最低，为24 ℃.

2) 晴朗天气下，07:00到中午13：00，电暖器逐渐放热，其表面平均温度为67.2 ℃，逐时降低，但由于室外温度逐渐提高，房间热负荷降低，气候室内温度依然能保持在17 ℃以上；当电暖器表面温度与室外温度同时降低的下午，室内平均温度降幅加大，在下午16：00左右，电暖器平均表面温度为42 ℃，室内平均温度低至16 ℃.

3) 在距离电暖器放热侧3.9 m范围内，在无人为因素干扰的情况下，各断面温差波动较小，尤其是蓄热开始后5 h以及再次蓄热前11 h内，各断面平均温度无显著差异；其余时间，最远断面与最近断面平均温度差值超过0.6 ℃，最高1.15 ℃.

图6 不同纵断面测点的平均温度随时间的变化Fig.6 Variation of the average temperature of different longitudinal measuring points with time

相同工况下，不同横断面测点的平均温度随时间的变化规律如图7所示，三排测点分别距离地面400 mm，1 200 mm，2 000 mm.

由图7可以看出：

1) 不同高度的测点变化规律一致但温差较大，各位置测点温度随着高度的升高而升高。距地面400 mm的测点，只有20.8%的时间温度超过16 ℃，距离地面1 200 mm和2 000 mm的测点，分别有66.7%、79.2%的时间温度超过16 ℃.

2) 不同高度的测点可反映出人体头部和脚部附近空气温度，头脚温差大会出现热舒适性问题。

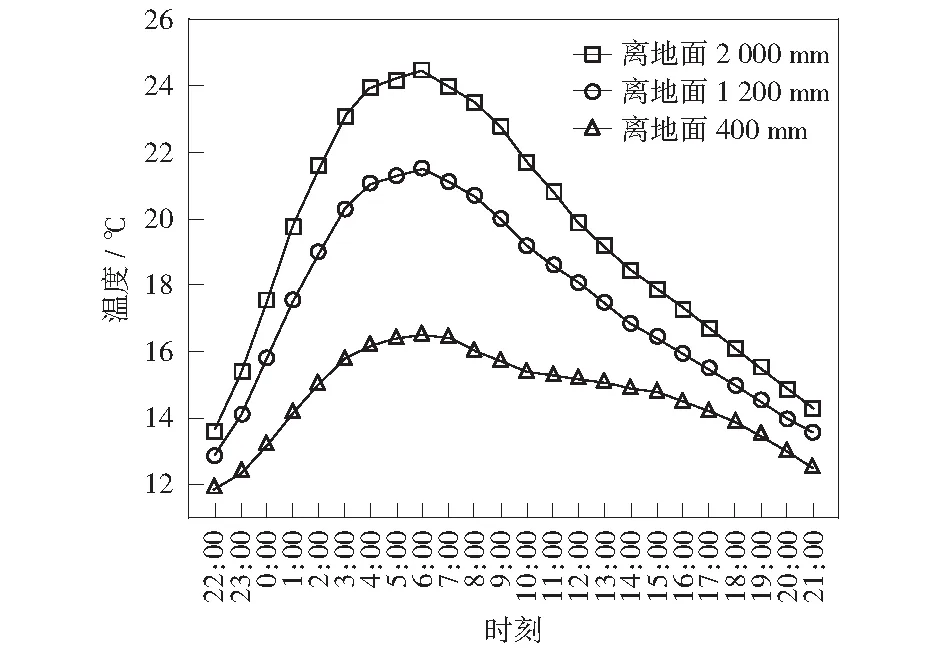
图7 不同横断面测点的平均温度随时间的变化Fig.7 Variation of the average temperature of different cross-section measuring points with time

通过MATLAB软件将人工气候室内每隔6 h的空气温度绘制成云图，如图8所示。因蓄热电暖器表面与室内空气温差较大，不容易直观地从图中反映室内温差的变化。

从图8中能反映出，电暖器在蓄热阶段室温均匀性较差，尤其是电暖器温度最高时；当电暖器停止蓄热，进入放热阶段时，室温逐渐趋于一致。

4.2 不同室外温度下室内温度场随时间和测点位置的变化

当电暖器蓄热时间一定，气候室室外温度不一定时，室内平均温度随时间的变化规律如图9所示。以晚22：00气候室室外温度T22为基准，比较室内温度差异。其中T22=9.27 ℃时，气候室室外日平均温度为9.34 ℃，相对湿度18%～57%，西南风1-2级。T22=10.10 ℃时，室外日平均温度为13.43 ℃，相对湿度16%～57%，西北风1-2级。T22=15.54 ℃时，室外日平均温度为15.82 ℃，相对湿度18%～55%，东北风1-2级。

由图9可以看出，蓄热时间一定时，室内温度与室外温度成正相关关系，室外温度越高，室内温度保持在峰值的能力越强。

4.3 不同蓄热时间下室内温度场随时间和测点位置的变化

当气候室外温度较为接近时，改变蓄热电暖器蓄热时间，得到室内平均温度随时间变化规律如图10所示。蓄热8 h时室外日平均温度为9.53 ℃，蓄热9 h时室外日平均温度为9.34 ℃，蓄热10 h时室外日平均温度为10.56 ℃.

图8 不同时刻室内气温云图Fig.8 Indoor temperature cloud map at different times

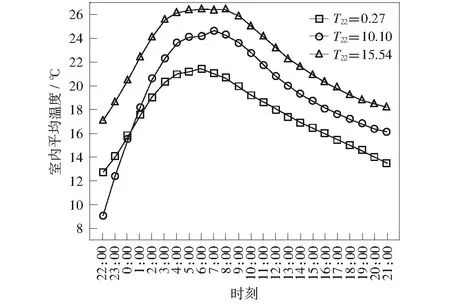
图9 不同室外温度下室内平均温度随时间的变化Fig.9 Variation of indoor average temperature with time under different outdoor temperatures

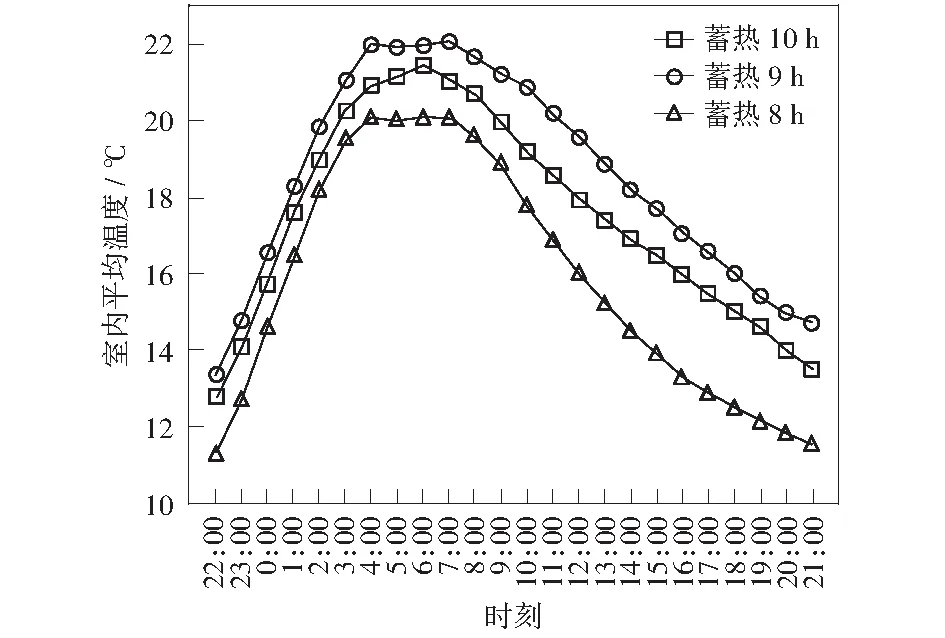
图10 不同蓄热时间下室内平均温度随时间的变化Fig.10 Variation of indoor average temperature with time under different heat storage time

随着蓄热时间的增加，室内所能达到的最高温度几乎不变，但维持较高舒适性的能力逐渐增强。在放热阶段，蓄热时间越长，热量散失越快。

5 结语

采用实验的方法研究了显热蓄热式电暖器供暖条件下室内温度场的变化规律，主要结论如下：

1) 显热蓄热电暖器蓄放热能力较强。当室外最高温度为0～5 ℃，最低温度为-10～-15 ℃，风力在5级以下时，蓄热时间合理的情况下，蓄热停止后，温度在16 ℃以上至少能保持16 h.房间水平温度梯度较小，温度较为均匀，垂直温度梯度较大，离地面1.2～2.0 m的范围内能长时间处于比较舒适的温度带，但头脚温差较大，会产生不舒适感。

2) 室内温度随时间变化规律与室外温度以及蓄热时间有较大关系，室外温度越高，蓄热时间越长，室温停留在舒适范围内时间越长，电暖器保持其高温状态的能力也越长。当天气寒冷时，可适当增加蓄热时间，以提高室内舒适性。9～10 h是较为合理的蓄热时间。合理地结合室外气温变化调整蓄热时间能有效降低供暖能耗，节省运行费用。

3) 算术平均值与中位值均能反映部分区域温度分布情况，中位值不容易受到极端数据值的干扰，能更有效地代表区域温度的整体情况。

研究结果有助于研发设计工作者更直接地了解蓄热电暖器蓄散热特性和使用状况，为优化改进蓄热电暖器提供参考，重点在于提高蓄热电暖器的蓄热能力、改进放热模式以提高室温均匀性等。