纵轴式掘进机截割头载荷影响因素的仿真分析

2020-06-02冯君玲田慕琴贺颖王茜

工矿自动化 2020年5期

冯君玲，田慕琴，贺颖，王茜

(1.太原理工大学矿用智能电器技术国家地方联合工程实验室, 山西太原 030024；2.太原理工大学煤矿电气设备与智能控制山西省重点实验室, 山西太原 030024)

0 引言

纵轴式掘进机是矿井巷道开拓过程中的重要设备，其可靠性和工作效率是煤矿安全高效生产的必要保证[1]。掘进机工作时，作用于截割头的载荷会受到截割煤岩物理机械特性、掘进机结构参数、操作参数及运动参数等因素影响。若掘进机结构参数与所截割煤岩特性不匹配，或者操作参数和运动参数选择不合理，将引起截割头载荷的剧烈波动，导致掘进机截齿、截割电动机、油缸等部件发生故障或损坏，从而降低掘进机的截割性能，影响煤矿的生产效率[2]。

国内外学者对掘进机截割头载荷特性及其变化规律进行了大量研究。张梦奇[3]基于单截齿破岩试验的相关理论，对纵轴式掘进机截割头横摆工况载荷进行了模拟研究，分析了截割头从开始接触煤岩至稳定工作状态中的载荷特性，通过频域分析发现截割头载荷受转频、截齿配置形式及螺旋线数量的影响显著。王想[4]对纵轴式掘进机截割头同时截割2种不同普氏系数煤岩的过程进行了数学描述，采用仿真方法对其载荷进行研究，分析了分层面夹角对载荷及其波动的影响规律。李媛媛等[5]采用有限元仿真方法对截割头截割过程进行动态仿真分析，得到了截割头三向力随煤岩普氏系数的变化规律。蔡文安等[6]利用自行设计的截割试验台，根据不同截割转速和进给速度相配合，对煤粉水泥配比为3.6∶1的煤岩进行截割试验，通过分析得到了最佳运动参数组合，为掘进机实际截割操作和掘进机自动化提供了参考依据。

以上研究采用试验方法或仿真手段对截割头载荷进行模拟，但只是分析单一因素对载荷及其波动的影响规律，且主要针对的是截割头设计、掘进机选型及系统改进等问题。然而掘进机实际截割过程中受到其内部及外部多种因素的综合影响，这些因素之间相互关联，仅研究单一因素的影响规律并不能全面反映截割头载荷及其波动的变化，鉴此，本文采用Matlab编程语言，针对纵轴式掘进机的水平截割工况，对影响截割头载荷的多种因素进行了较为全面的仿真分析，得到了各向载荷及其波动随各因素的变化规律。仿真结果可为掘进机掘进过程中操作参数和运动参数的合理选择提供理论依据，以增强掘进机工作平稳性，提高掘进生产效率，延长掘进机使用寿命。

1 截割头水平截割的载荷模拟及载荷波动模型

1.1 截割头水平截割的载荷模拟

单个截齿截割岩石时，其所受截割阻力Zi、牵引阻力Yi、侧向阻力Xi[7]为

Zi=Pk[ktkgky(0.25+0.018tihi)+0.1S]

(1)

(2)

Xi=Zi[(C1/(C2+hi)+C3)hi/ti]

(3)

将各个截齿三向力分别沿截割头坐标a，b，c分解为Ra,Rb,Rc，再对各个时刻参与截割的截齿受力进行求和，即得到截割头处于任一位置j时，作用于截割头的升力Raj、横向阻力Rbj、推进阻力Rcj和负载转矩Mj分别为[7]

(4)

(5)

(6)

(7)

式中：mj为截割头处于j位置时参与截割的截齿总数；βi为第i个截齿的安装轴线相对于齿尖回转平面的倾斜角；rgi为第i个截齿的齿尖回转半径。

依据式(1)—式(7)，在Matlab中编制截割头载荷模拟程序[8]，输入某纵轴式掘进机截割头(截割头截齿排列为交叉式)的结构参数(表1)，得到f为7时截割头完全钻入岩壁后旋转三周的截割载荷模拟曲线，如图1所示。表1中,t为平均截线距,L0为截割头轴向长度,D为截割头大端直径。

表1 截割头结构参数

由图1可知，水平截割工况下，截割头三向载荷大小关系为Ra>Rb>Rc；随着各时刻参与截割的截齿数发生变化，截割头三向载荷也发生变化，并呈现周期性波动，且横向阻力和升力波动较大，推进阻力基本维持稳定。

图1 截割头载荷模拟曲线

掘进机水平截割工况下截割头载荷及工作参数如图2所示，由式(1)—式(7)可知，截割头工作载荷主要受截割岩石特性参数、截割头设计参数、某一瞬时参与截割的截齿数及截割头转速和截割臂摆速等因素的影响。其中每一瞬时参与截割的截齿数由截割头设计参数、截割头钻入工作面深度(掏槽深度L)、截割头吃刀深度d共同确定，对于特定工作面选定的掘进机，其截割头结构参数在设计过程已经确定，在工作过程中无法调节[9]，因此，截割岩石特性参数、截割头掏槽深度、截割头吃刀深度、截割头转速和截割臂摆速成为影响截割头瞬时载荷的主要因素。

(a) 截割头载荷

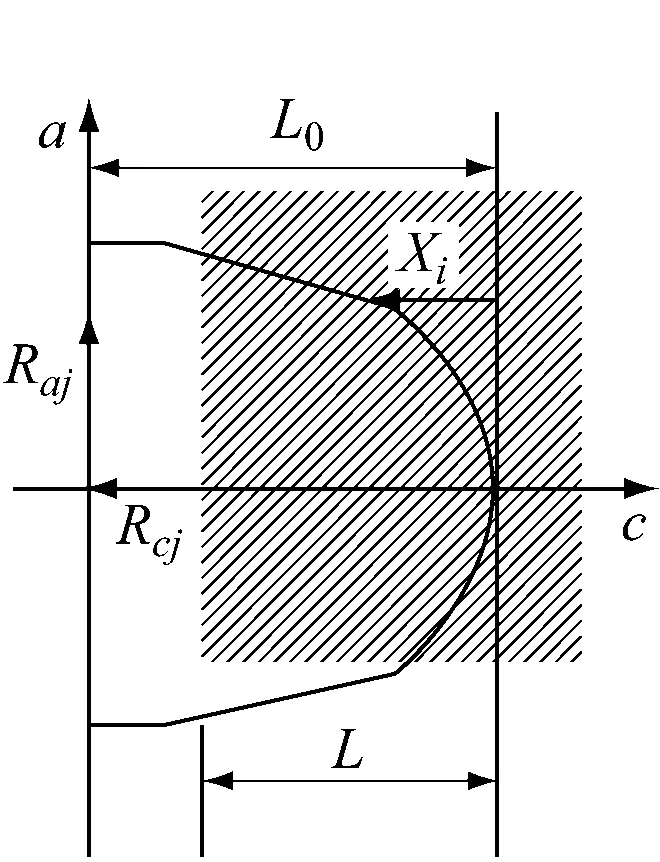
(b) 截割头工作参数

1.2 截割头载荷波动模型

掘进机截割岩壁时，每一瞬时参与截割的截齿数目和受力状态都会发生变化，截割头每转一周，其所受的载荷会产生波动；截割工作面地质条件复杂多变且具有一定的随机性，加上掘进机自身的结构特点，人工操控掘进机不准确，导致掘进机操作参数和运动参数产生较大随机性，使截割头受力随截割臂的运动时刻变化[10]，产生波动。截割头载荷波动会引起机身振动、掘进机关键部件发生故障甚至损坏；使掘进机在截割过程中产生机身偏向角，机身偏向角的产生和变化会严重影响掘进机的定向掘进，使截割断面出现偏差，降低巷道成形准确度与精度[11-13]。因此，有必要对截割头载荷波动规律进行研究。

截割头载荷波动可以用载荷变差系数来表示，它是载荷的均方差σR与载荷均值ER的比值，即

(8)

(9)

式中：RI为截割载荷在I时刻的离散值；N为离散点数。

2 截割头载荷影响因素仿真分析

采用岩石普氏系数作为截割岩壁特性的定量表征[5]，将某纵轴式掘进机的相关设计参数代入截割头载荷模拟程序中，通过分别改变截割岩壁普氏系数f、截割头掏槽深度L、截割头吃刀深度d、截割头转速n和截割臂摆速v的值，可以得到各参数对截割头载荷的影响规律。

2.1 截割岩壁普氏系数对截割头载荷的影响

根据普氏系数可对煤岩进行划分：当f小于4时为煤；当f为4～8时为中等坚固岩石；当f大于8时为坚固岩石。本文研究对象为纵轴式掘进机，因此，f的取值范围为4～10。当n=40 r/min,v=1.2 m/min,L=L0,d=D时截割头载荷均值及变差系数随f变化曲线如图3所示。

由图3(a)可看出，随着f的增大，截割头三向载荷及负载转矩均随之增加，这是由于f越大，岩壁破碎难度越高，所需截割力越大，其中，截割升力、推进阻力和负载转矩与f近似呈线性相关，而横向阻力则随f的增加呈指数形式增长；由于截割头完全钻入岩壁，所以,参与截割齿数的均值为定值17，大约是截割头总截齿数的一半(该掘进机截割头装配36把截齿)。由图3(b)可看出，水平截割时，在其他参数不变的情况下，截割头横向阻力波动随着f的增大而减小，截割头升力波动随着f的增大而近似线性增大，推进阻力和负载转矩波动则相对平稳，几乎不随f的变化而变化，说明截割载荷的波动并不随f的增大而增强。

2.2 截割头掏槽深度对截割头载荷的影响

截割头掏槽深度L是在截割头钻入岩壁后，水平截槽在工作面推进方向的深度，即截割头钻入岩壁的深度[14]。为了研究截割头掏槽深度对载荷的影响规律，在此定义截割头掏槽深度比λ为截割头掏槽深度与截割头轴向长度L0的比值，即

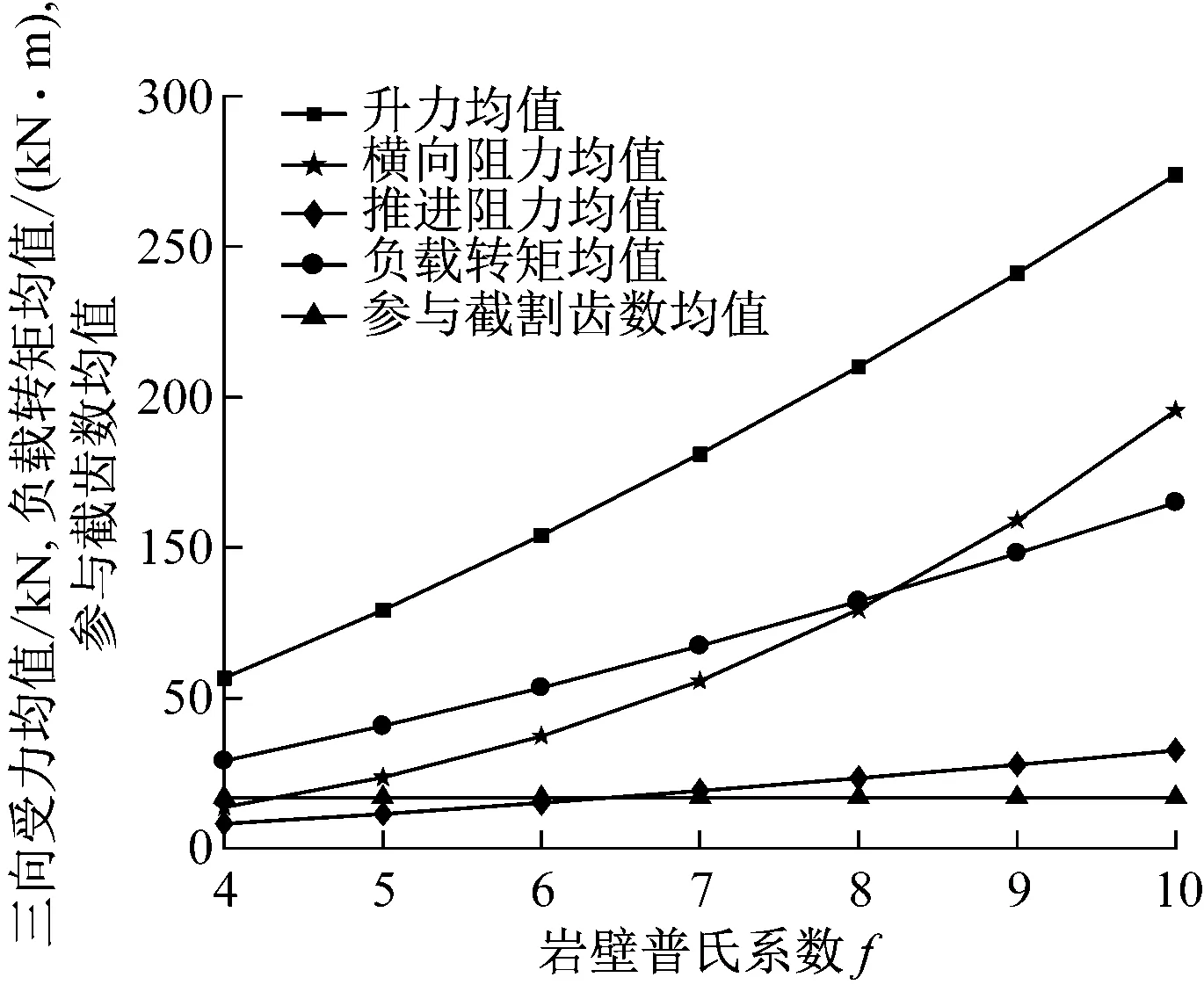
(a) 载荷均值随岩壁普氏系数f变化曲线

(b) 载荷变差系数随岩壁普氏系数f变化曲线

(10)

当n=40 r/min,v=1.2 m/min,f=7,d=D时截割头载荷均值、参与截割截齿数均值及变差系数随λ变化曲线如图4所示。

由图4可看出，随着λ的增加，参与截割的截齿数增加，截割头各向载荷亦随之近似呈线性增大，且升力增加幅度最大，推进阻力增加幅度最小；各向载荷波动中，横向阻力载荷波动高于其他方向载荷波动，且各向载荷波动随着λ的增大而减小，特别是横向阻力波动减小得更为明显。因此，截割头掏槽深度应等于或者接近于截割头轴向长度，这样不仅有利于降低截割头振动，而且能够有效提高生产率。

2.3 截割头吃刀深度对截割头载荷的影响

截割头的吃刀深度d是掘进机往返截割时沿工作面高度方向的截割深度，其大小对截割头的载荷、掘进机工作的稳定性有直接的影响[14]。定义截割头吃刀深度比γ为截割头吃刀深度与截割头大端直径D的比值，即

(11)

当n=40 r/min,v=1.2 m/min,f=7,L=L0时截割头载荷均值、参与截割截齿数均值及变差系数随γ变化曲线如图5所示。

(a) 载荷均值随掏槽深度比λ变化曲线

(b) 参与截割齿数随掏槽深度比λ变化曲线

由图5可看出，随着γ增加，参与截割的截齿数增加，升力均值明显增大；推进阻力均值先有小幅增加，后趋于平稳；横向阻力均值先增加，在γ=0.6时达到最大，随后随γ的增加而减小。升力波动远高于其他方向载荷波动，随着γ的增加，其波动显著降低；横向阻力波动随着γ的增加先显著降低,后略有升高，在γ=0.6时达到最低；推进阻力波动随着γ的增加也明显下降。因此，综合来看，为了减小截割头载荷波动，提高生产率，掘进机在一个横摆截割过程结束后，截割头升降摆动距离应等于或者接近于截割头大端直径。

2.4 截割头转速和截割臂摆速对截割头载荷的影响

掘进机截割头在截割电动机以及截割臂的带动下可以完成煤岩的破碎，从而实现掘进工作[15]。依据第1.1节的分析可知，截割头转速和截割臂摆速通过影响单个截齿的瞬时切屑厚度影响单个截齿的瞬时三向载荷，进而影响截割头的三向载荷以及掘进机的工作效率。为了分析其影响规律，设置L=L0,d=D，截割头以不同的转速n和截割臂摆速v截割f为7的均匀岩壁，得到截割头载荷变化及波动曲线,如图6—图8所示。

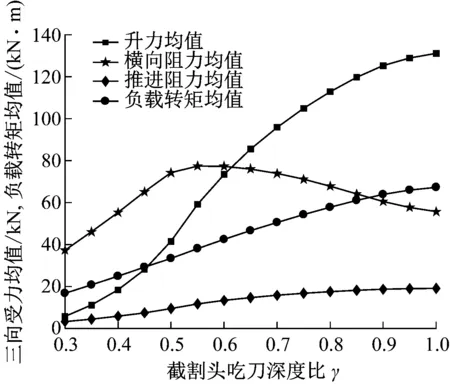
(a) 载荷均值随吃刀深度比γ变化曲线

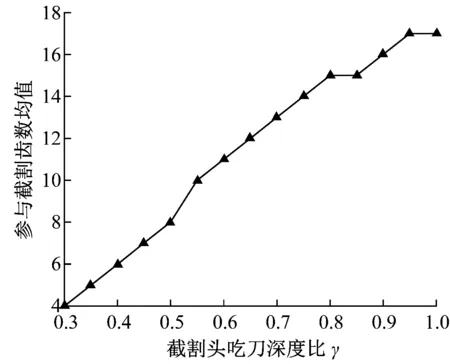
(b) 参与截割齿数随吃刀深度比γ变化曲线

(d) 载荷变差系数随吃刀深度比γ变化曲线

(a) 载荷变差系数

(b) 载荷均值

(a) 载荷变差系数

(b) 载荷均值

由图6—图8可看出，在n一定的情况下，三向载荷均值均随着v的增加而增大；在同一摆速下，三向载荷均值随着n的减小而增大。这是由于v增加或者n减小使得单个截齿瞬时切屑厚度增加所致。三向载荷中，横向阻力波动明显高于升力和推进阻力波动，横向阻力变差系数和推进阻力变差系数按截割头载荷规律变化，升力变差系数与之相反。因此，应合理选择n和v，在f较小时，截割阻力小，可适当增加n和v，以提高掘进效率；在f较大时，应相应降低n和v，以减小截割阻力和截齿磨损。虽然提高n能够减小切屑厚度，降低载荷，但同时也会降低截齿的截割能力，所以,不宜采用。实际应用中可以采用多目标优化方法，找到相应f下对应的n和v组合，在保证掘进机正常工作前提下，尽量减小截割头载荷,降低其波动程度。