多任务深度卷积网络的CT图像方向校正
2020-06-02林家庆韩娟袁直敏彭佳林
林家庆, 韩娟, 袁直敏, 彭佳林
(华侨大学 计算机科学与技术学院, 福建 厦门 361021)
医学图像理解的计算机辅助诊断/手术中,医学图像预处理是一个重要的步骤,是后续图像融合、目标检测和分割等任务的重要基础[1].实现图像的方向校正最直接的方法是刚性配准,但配准方法通常只适用于方向偏差较小的情况,当偏差角较大时,配准结果准确性仍有不足[2].Wei等[3]利用图像旋转后的插值阴影来进行旋转角度判别计算;Solanki等[4]通过打印出的图像的像素点特征来判断旋转角度.通过背景水平线检测来校正方向是一种常用的自然图像方向校正方案,但并不适合医学图像[5].此外,一些研究者们将旋转角度控制在90°的倍数来进行方向校正研究[6],但没有解决连续值情况.基于深度学习方法的头部和手部等特定类别图像的方向校正[7-12]的研究取得一定进展.Fischer等[13]尝试通过难度划分进行方向校正;de Vos等[14]尝试使用深度网络对图像进行局部的配准校正.但这些研究只能对图像进行略微调整且主要针对自然图像,而医学图像上方向校正的主要方法还是配准[15].
深度学习方法虽然在数据充足的情况下可以表现出优异的性能,但在数据稀缺时则表现一般.因此,如何构建在小样本训练集下的深度学习方向校正方法,也是医学图像方向校正领域的一个主要挑战.为解决上述方法的局限性,本文提出一种基于深度卷积网络的图像旋转和翻转的校正方法,以腹部CT(computed tomography)图像数据集作为训练和验证集进行实验验证.
2 研究方法
2.1 大样本下并行卷积回归网络
在训练样本充足(大样本)的情况下,建立并行卷积回归网络(parallel convolutional regression network,PCRN)来完成大样本下的方向校正任务,着重考虑网络生成预测结果的效率.即采用PCRN提取两个子任务的共享特征及专有特征,然后通过在最终层接上不同的回归器,同时完成两项子任务的回归.在面对侧旋角度回归和翻转状态回归两个回归任务时,模型使用共同的浅层特征生成各自任务相关特征完成多项任务的回归.网络结构如图1所示.
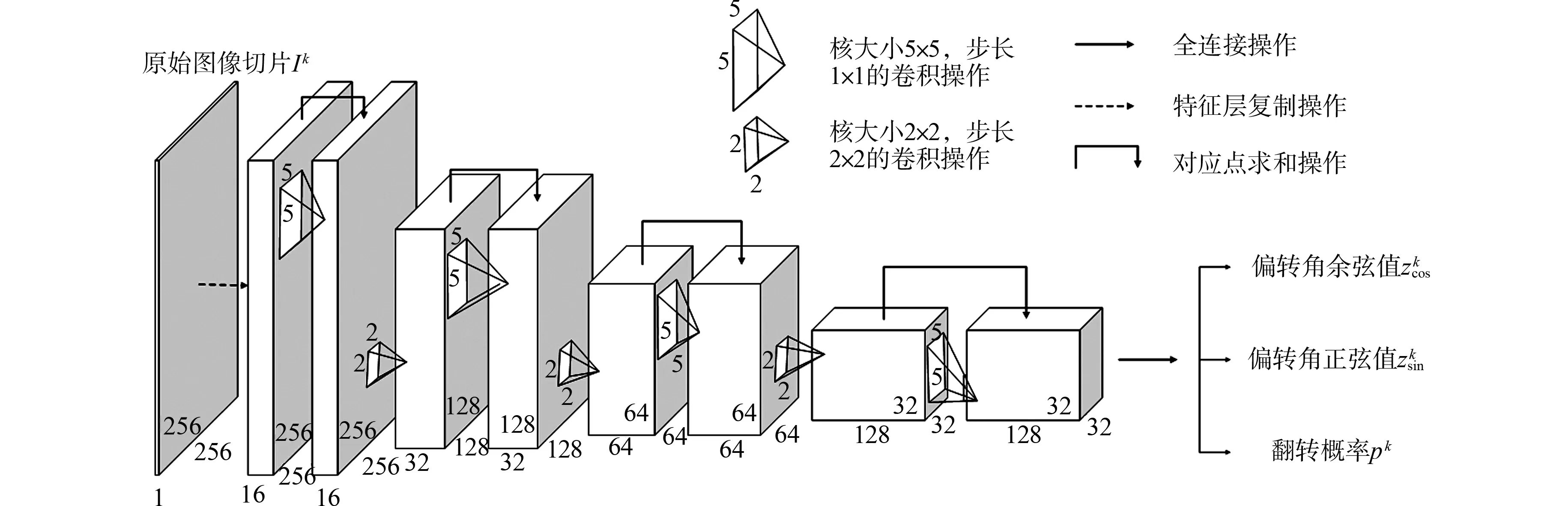
图1 并行卷积回归网络结构图Fig.1 Network structure of parallel convolution regression network
该网络整体上是一个特征编码残差网络,分为数据输入、特征提取、参数输出三个部分.具体地,PCRN网络输入部分包含一个复制层,将原始图像进行冗余复制,以便后续的残差连接;特征提取部分包含4个残差模块和3个下卷积层.其中每两个残差模块间使用卷积核大小为2×2,步长为2×2的下卷积层进行连接以压缩特征编码;每个残差模块中使用的卷积核大小为5×5,步长为1×1.受Highway神经网络和残差网络的启发[16-17],残差模块中的浅层和深层特征间使用Shortcut连接,使其中的卷积过滤器学到更容易习得的特征间残差[16,18],从而提高最终输出结果.

图2 正余弦值符号与所在象限的关系Fig.2 Relationship between sine-cosine symbols and quadrants
网络中的残差模块和下卷积层使用ReLu函数进行激活;参数输出部分包含一个全连接层,其输入为特征提取部分最后一层输出的高层语义特征,输出为预测偏转角余弦值、预测偏转角正弦值,以及图像翻转概率等3个目标方向校正参数.选用侧旋角度的正弦值和余弦值作为预测输出的原因是,使角度到输出的映射函数在(-180°,180°]范围均匀和连续[19].上述全连接层侧旋校正输出使用Tanh激活函数,翻转概率输出使用Sigmoid激活函数.


(1)

(2)
文中使用的偏差角回归损失函数为均方误差损失,即为
Lang=(cos(gt)-zcos)2+(sin(gt)-zsin)2.
(3)
式(3)中:gt为图像偏转角度真值;zcos,zsin分别为网络输出预测偏转角的余弦值和正弦值.
翻转概率逻辑回归使用交叉熵损失,即
Lrev=-(r·lgp+(1-r)·lg(1-p)).
(4)
式(4)中:r为图像翻转真值,翻转为1,否则为0;p是网络判断图像为翻转的概率输出.
总损失函数L为两个损失函数之和,即
L=Lang+Lrev.
(5)
在样本数量充足的情况下,PCRN只需一次前向传播就能生成所有结果,速度快且效率高;但在样本数量较少的情况下,PCRN的校正能力仍有限.
2.2 小样本下串行卷积回归网络
在训练样本稀缺(小样本)的情况下,采用串行卷积回归网络(serial convolutional regression network,SCRN)先完成较为简单的侧旋角度回归任务;然后,通过预测的校正角度将图像基本转回正位,继而对图像进行翻转判定,如图3所示.

图3 串行卷积回归网络结构图Fig.3 Network structure of serial convolutional regression network

图4 坐标旋转变换示意图Fig.4 Demonstration of coordinate rotationtransformation
首先构建侧旋校正网络预测三维图像侧旋角度α,然后通过α将图像基本调回正位,最后再使用翻转判定网络对基本处于正常位置的图像进行翻转判定.该方法中的两个网络与“并行卷积回归”中的网络基本相同,不同点在于:前面的侧旋校正网络少了翻转概率输出,后面的翻转判定网络少了侧旋角度正弦值和余弦值输出.
在侧旋校正阶段,按照PCRN方法可以预测三维图像I的偏转角α.图4为坐标旋转变换示意图.对于经旋转α角度后的图像I上的每一点(x′,y′),应用坐标旋转公式

(6)
计算出其旋转前坐标(x,y).由于图像像素点坐标为整数,通过双线性插值方法可以求得旋转α前的图像I.该阶段使用式(3)所述的损失函数.
在翻转判定阶段,训练时对未发生侧旋的输入切片进行[-5°,5°]范围内的随机侧旋,以模拟侧旋校正网络的输出偏差.测试时输入经过侧旋校正网络校正后的切片,通过输出翻转概率判定原图是否发生了翻转.该阶段使用式(4)所述的损失函数.
3 实验结果与分析
3.1 实验设置
在实验中,训练和验证数据使用ISBI 2017肝脏肿瘤分割竞赛训练数据集中的130个三维CT扫描图像.其中,100个为训练数据,30个为验证数据.测试数据集使用Codalab肝脏肿瘤分割竞赛测试数据集中的70个CT扫描图像.对训练数据进行如下预处理:1) 截取数据灰度范围到[-100,250],以消除大量无用的灰度信息,再等比例缩放到[0,1];2) 在垂直方向上截取从盆骨上沿到胸腔下沿的图像区域;3) 将每个三维图像数据在垂直方向上进行切片,并将分辨率从512 px×512 px下采样到256 px×256 px,以减小深度网络的体积和计算负荷;4) 将切片数据在(-180°,180°)范围内进行随机旋转,以作为训练输入数据;5) 对切片数据随机进行倍数范围在[0.95,1.05]的尺度缩放和灰度缩放.
为精确测量对比几种方向校正方法的能力,实验中对测试和验证数据进行了扩充.即除了对每个数据进行了上述灰度范围处理和区域截取外,还将每个区域截取后的三维数据切分为腹腔下部、腹腔中部和腹腔上部等3个区域.由此,总测试数据就达到70×3=210个,验证数据达到30×3=90个.对所有测试数据,实验先随机抽取50%进行翻转,再随机抽取50%变换为侧旋角度在(-180°,-90°]和[90°,180°]范围内的“大角度”样本,剩下的随机变换为侧旋角度在(-90°,90°)范围内的“小角度”样本.对于验证数据也进行以上操作.另外,考虑到现实中医疗图像数据通常较为稀缺,从100个训练数据中抽取10个作为小样本训练数据集,在实验中对训练样本稀缺时的深度学习方向校正方法也进行了研究.
文中模型训练阶段,网络使用Adam优化方法进行网络参数优化.Adam动量参数按照文献[20]的推荐,设β1=0.9,β2=0.999;初始学习率设为λ=1.0×10-4, 在训练中逐步递减,最小到λ=1.0×10-5;批量大小为24,翻转判定阈值为0.9.除了按照节2所述使用切片校正结果中位数代表三维图像校正结果,实验中还使用切片校正结果均值代表三维图像校正结果以便对比分析.实验评价指标分为侧旋校正和翻转判定两个方面,前者使用平均误差角度作为评价指标,后者使用错判率作为评价指标.
3.2 用于对照的基线方法
以传统配准校正方法作为基线方法进行对照比较.实验选取的参考切片和待校正切片大体在人体同一位置,以确保配准效果良好.由于参考切片和待配准切片内部结构较为相似并且图像本身不存在形变,因此考虑使用仿射变换进行配准[2].配准的变换参数定为缩放倍数、平移向量和旋转角度等3个参数,并在配准完成一次后将图像进行翻转后再次进行配准,通过比较两次配准的最优结果来判断图像是否发生了翻转.配准度量方法为平均平方误差,配准过程中的优化方法为梯度下降法.
进一步的,考虑到待配准切片和参考切片在腹腔内部细节上存在不同,实验考虑屏蔽内部细节差异以进一步提高旋转校正配准精度,并设计了第二种配准方法.即先将参考图像和待校正图像切片进行躯干内部填充,屏蔽掉躯体内部差异,使其成为简单的类椭圆二值图形;然后,按照第一种方法进行仿射变换配准.第二种方法由于屏蔽了腹腔内部细节差异而腹腔外形又为左右对称结构,翻转预测预期较差.最后,对于每个三维图像的方向校正结果,使用该图像中抽取切片的测试结果统计量,如平均值或中位数,作为三维图像方向校正最终值.
3.3 结果分析
在样本充足下,PCRN和基线方法估算的平均方向偏差测试结果,如表1所示.

表1 样本充足下PCRN和基线方法估算的平均方向偏差Tab.1 Average orientation error estimated by PCRN and baseline method on dataset with sufficient samples (°)
由表1可知:样本充足情况下,文中所提出的深度学习“并行卷积回归”方法对比参考方法在小角度情况下有略微的优势.进一步深入了解发现,参考方法的校正结果受配准时选择的参考切片影响较大.图5为配准方法的多最优解情况.从如图5可知:当选择的参考切片与待配准切片外形差别较大时,就可能出现多最优解的情况,从而导致校正效果不佳,而文中提出的方法能较好地解决该问题.
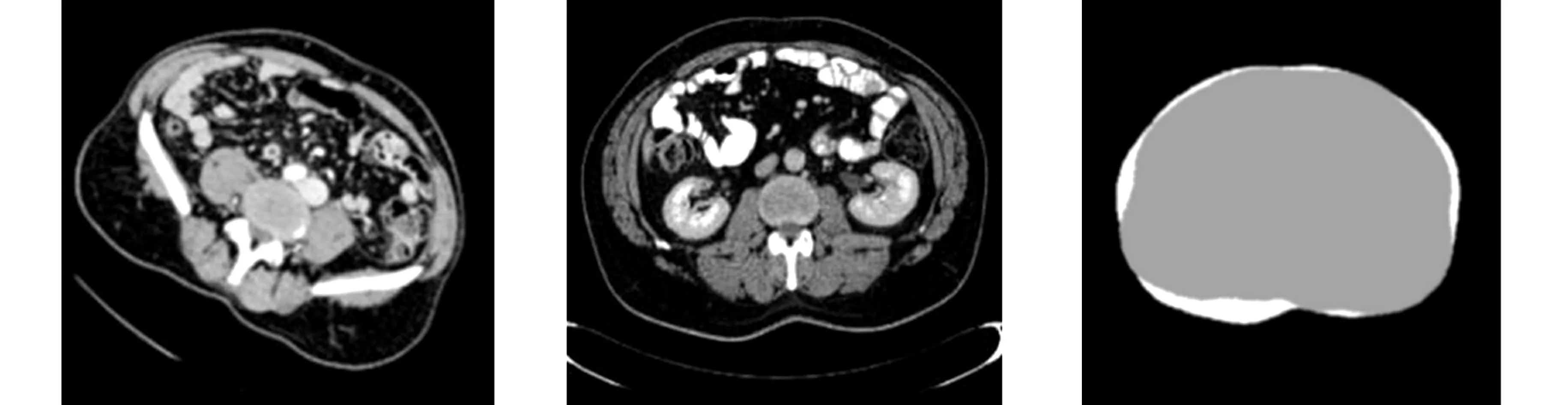
(a) 待配准切片 (b) 参考切片 (c) 配准的第一种最优结果

(d) 内部填充后的待配准切片 (e) 内部填充后的参考切 (f) 配准的第二种最优结果 图5 配准方法的多最优解情况Fig.5 Multiple optimal solutions of registration method
由表1还可知:文中所提出的深度学习“并行卷积回归”实验结果中,中位数统计结果与小角度情况下并无太大差异,而均值统计结果则明显较差.图6为校正角度符号相反的结果图.由图6可知:在极大角度情况下,校正角度在绝对值上差异不大,符号却可能相反,导致均值受巨大影响.
参考方法取得局部最优的典型示例,如图7所示.由图7可知:参考方法可能因优化方向错误导致最终结果陷入局部最优,所以在大角度情况下的校正结果明显差于文中所提的方法.

(a) 侧旋角度为-177°的切片a (b) 将a校正177°后的图像 (c) 将a校正-179°后的图像 图6 校正角度符号相反的结果示意图Fig.6 Results of the opposite correction angle sign

(a) 待配准切片 (b) 参考切片 (c) 待配准切片校正结果

(d) 内部填充后的待配准切片 (e) 内部填充后的参考切片 (f) 正确的校正结果 图7 参考方法取得局部最优的典型示例Fig.7 Typical examples of local optimal solution by reference method
PCRN典型方向校正结果,如图8所示.由图8(a),(b),(d),(e)可知:在样本充足情况下,文中提出的深度学习“并行卷积回归”方法在侧旋校正和翻转判定两个子任务上都取得了优异的表现.这说明网络充分的提取了图像的侧旋校正特征和翻转判定特征.进一步,通过对错判的翻转样本分析得知,由于图像内左右辨识特征太过稀少,样本本身辨识度太低,导致切片翻转判断错误(如图8(e),(f)所示).在实际应用中,通过统计同一个三维图像的整体翻转标识来避开该问题.参考方法中的原始配准方法由于配准误差大,导致翻转的最终判定受到较大影响,准确率较低;而内部填充的配准方法则基本没有翻转辨识的能力.
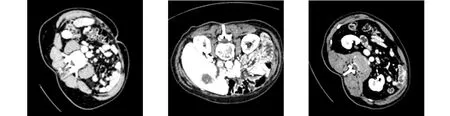
(a) 小角度下典型切片a (b) 大角度下典型样本切片b (c) 左右相似的难分样本c

(d) 切片a校正结果 (e) 切片b校正结果 (f) 切片c校正结果图8 PCRN典型方向校正结果展示Fig.8 Typical orientation correction results by PCRN
在样本稀缺下,SCRN和PCRN估算的平均方向偏差测试结果,如表2所示.由表2可知: 在样本稀缺情况下,使用SCRN方法侧旋校正效果接近表1中样本充足下的侧旋校正效果,且比样本稀缺下的PCRN方向校正效果好.此时,PCRN在小角度侧旋校正方面已经不如内部填充的配准方法.在翻转校正上,由于样本数量太过稀少的原因,PCRN翻转识别能力相比于样本充足情况下下降较多.但可以看到SCRN方法此时在翻转偏差平均值上,还是明显优于PCRN方法的.
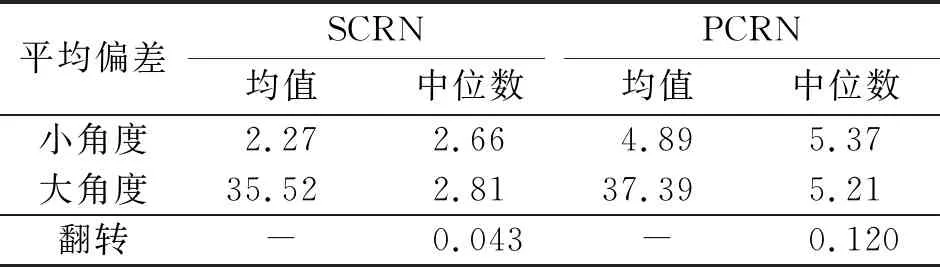
表2 样本稀缺下SCRN和PCRN估算的平均方向偏差Tab.2 Average orientation error estimated by SCRN and PCRN on dataset with limited samples (°)
4 结论
将复杂的CT图像方向校正任务分解为简单的侧旋角度校正回归和翻转概率逻辑回归两个回归子任务,并针对不同样本数量的数据集,分别以并行和串行的方式设计了两种多任务深度学习网络——PCRN和SCRN.
经典的仿射配准方法需要在同时估计缩放、平移参数和旋转参数情况下,才能实现较为准确的旋转和翻转估计.而文中提出的神经网络方法一个最大优势是,可以在无需估计缩放和平移的前提下,实现对旋转和翻转的更精准估计.在公开数据集上的实验结果证明文中提出的方法,在小角度侧旋、大角度侧旋和翻转判断上都有着较强的校正能力,具有很强的应用价值.后续研究将把串行回归的两个网络连接到一起,实现直接的端到端输出,以简化训练过程,提高模型精度.
