横风激扰下的跨座式单轨车辆运行平稳性分析
2020-06-02李军魏睿隗寒冰周伟
李军, 魏睿, 隗寒冰, 周伟
(1. 重庆交通大学 机电与车辆工程学院, 重庆 400074;2. 重庆交通大学 城市轨道交通车辆系统集成与控制重庆市重点实验室, 重庆 400074)
跨座式单轨交通具有小曲率线径运行的特点,在强横风作用下,跨座式单轨车辆可能脱离行驶轨面.目前,学者们对风荷载作用下的列车安全运行问题已进行了大量研究.彭祎恺等[1]对3种风载模型下的某型动车组头车侧风安全性进行对比分析,发现瞬态中国帽风载模型适合于我国高速列车的侧风安全评价.王康[2]引入瞬态中国帽风载模型及其计算方法,建立高速列车动力学仿真模型,对18种工况下的车辆安全性指标进行分析,得到在曲线外侧施加横风、曲线内侧施加横风和无横风等情况下高速列车的曲线通过安全性规律.曹亚博等[3]研究强阵风环境下高速列车的运行安全与脱轨边界,为阵风环境下高速列车的安全控制提供理论指导.Olmos等[4]建立一种有效的风-车-桥相互作用模型,并进行实验验证,以确定列车无法安全运行的临界风速和车速.Zhang等[5]研究基础因素对大跨度斜拉桥风轨车桥系统耦合振动的影响,发现车辆加速度在很大程度上受到风脉动和轨道不规则性的激励影响.
目前,关于风荷载作用下车辆安全性的研究主要集中于高速列车,较少涉及跨座式单轨交通[6],然而,在车辆模型、轨道线路等方面,跨座式单轨交通与高速列车具有明显的不一致性.基于此,本文对横风激扰下的跨座式单轨车辆运行平稳性进行分析,计算限值下的临界安全风速,得到横风激扰下跨座式单轨车辆运行的安全区域.
1 风载模型
1.1 瞬态中国帽风载模型

图1 瞬态中国帽风风速时间历程图Fig.1 Time history of transient Chinese cap wind speed
横风激扰模型可采用瞬态中国帽风载模型模拟自然界中的动态风场,风载模型中的动态阵风风速由稳定阵风风速和波动阵风风速叠加而成[7].任意一处的动态阵风风速u为
u(t)=u0(t)+ug(t).
(1)
式(1)中:u0为稳定阵风风速;ug为波动阵风风速.
以计算效率为前提,兼顾自然风脉动规律和极端变化情况,将模型进行简化.瞬态中国帽风风速时间历程图,如图1所示.图1中:umax为动态阵风最大风速;umin为动态阵风最小风速;t1~t8为动态阵风风速变化的作用时间;T为波动阵风持续时间.瞬态中国帽风载模型描述的动态阵风风速可由分段函数表示,即

(2)
式(2)中:A为umax与u0的比值,A=1.7.
由速度合成理论可知,合成风速uα和合成风向角α可由车速v、动态风速u和风向角αw合成,即

(3)
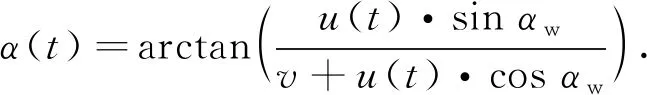
(4)
作用在车辆上的气动载荷可以简化为侧力Fy、升力Fz、倾覆力矩Mx、点头力矩My和摇头力矩Mz,根据准静态理论可得相关公式为
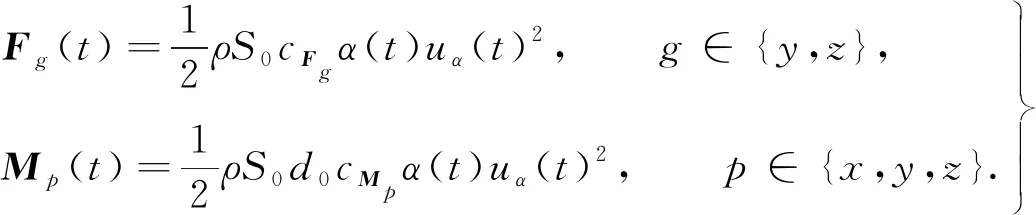
(5)
式(5)中:ρ为空气密度,ρ=1.225 kg·m-3;S0为迎风侧单轨车体投影等效面积,m2;d0为等效高度,m;cFg,cMp分别为气动力系数和气动力矩系数.
1.2 非定常随机风载模型
脉动风的风速功率谱是描述风速频率特性的重要参数,非定常随机风载模型采用经典且较为接近实际的达文波特(Davenport)风谱进行模拟.
Davenport脉动风功率谱经验表达式为
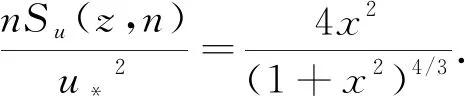
(6)
式(6)中:n为脉动风频率;Su(z,n)为脉动风风速功率谱;x为无量纲频率,x=1 200n/uave,uave为标准高度10 m处的平均风速;u*2=Kx2,K为地面粗糙度系数.
实际测量结果表明,近地层脉动风速根方差可近似计算,即σu≈2.5σ*,σv≈2.2σ*,σw≈1.35σ*.
据此,式(6)又可写为
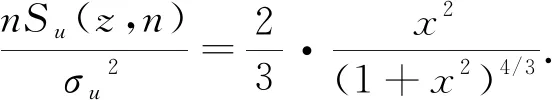
(7)
风场模拟采用谐波合成法,为了便于进行快速傅里叶变换(FFT),改用复指数形式表示,故一个零均值多变量一维平稳随机过程为
令Bjk(lΔω)=Hjk(lΔω)·exp(iφkl)(l=0,1,2,…,M-1),则式(8)可写为

(9)

图2 非定常随机风载风速时间历程图Fig.2 Time history of unsteady random wind speed
据此,通过N点FFT进行快速计算,根据计算结果再通过式(9)即可得到空间m点的随机脉动风速场,实际风速场为随机脉动风速场与当地平均风速之和.
非定常随机风载风速时间历程图(平均风速为15 m·s-1),如图2所示.
根据准静态理论和合成风速理论,可得到非定常随机风载模型[8-10].在跨座式单轨车辆模型中,风载荷以时间激励函数的方式输入,作为列车所受的外力激扰.
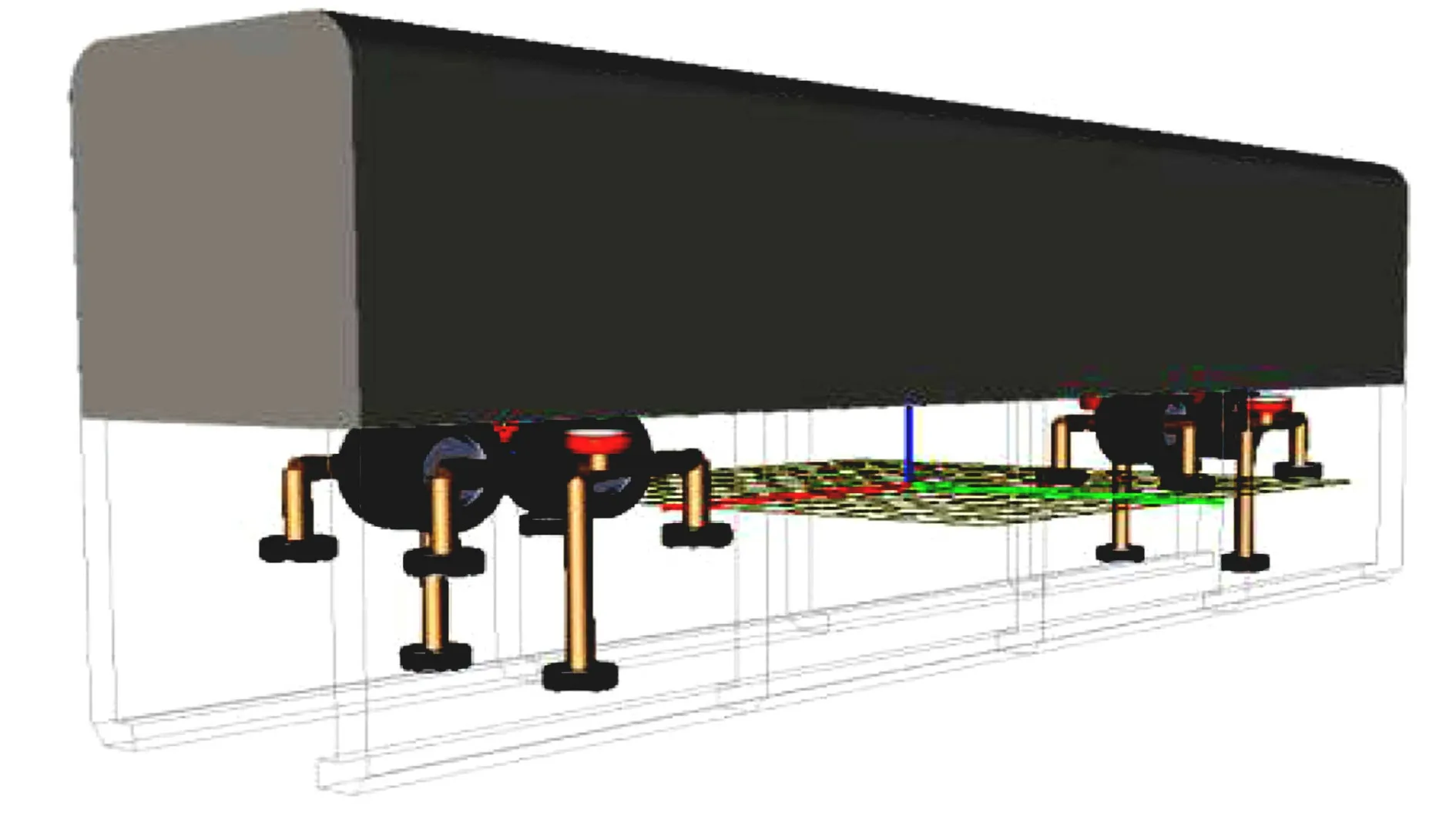
图3 跨座式单轨车辆模型Fig.3 Model of straddle monorail vehicle
2 跨座式单轨车辆动力学建模
2.1 跨座式单轨车辆动力学模型
跨座式单轨车辆的组成结构为车体、前后转向架、走行轮轮对、导向轮轮对和稳定轮轮对.走行轮、导向轮和稳定轮均使用橡胶轮胎,在模型中常常将其简化为并联的线性弹簧和阻尼器.轮对不设一系悬挂,只设由空气弹簧组成的二系悬挂[11-12].
利用多体动力学软件建立跨座式单轨车辆模型,如图3所示.该模型共计38个自由度,车辆主要动力参数,如表1所示.

表1 车辆主要动力参数Tab.1 Main dynamic parameters of vehicle
2.2 模型的验证
为验证模型的正确性,设置u=0,车速v分别为10,20,30,40,50,60,65 km·h-1,轨道线型为直线,轨道不平顺均采用常用且贴切的美国六级谱进行模拟,单轨车辆依次运行,并提取单轨车辆横向、竖向加速度数据.将处理后的仿真数据与文献[13]中实测的重庆轻轨加速度数据进行对比.仿真数据与实测数据的对比,如表2所示.表2中:av为竖向加速度;al为横向加速度.

表2 仿真数据与实测数据的对比Tab.2 Comparison of simulation data and measured data
当车速为65 km·h-1时,单轨车辆的加速度时程图,如图4所示.由图4可知:这些曲线是车体加速度的典型时程曲线.

(a) 竖向加速度 (b) 横向加速度图4 单轨车辆的加速度时程图Fig.4 Acceleration time chart of monorail vehicle
由表2和图4可知:模型仿真加速度与重庆实测数据[13]基本吻合.因此,可采用文中建立的仿真模型进行跨座式单轨车辆的动力学性能研究.
3 动力响应分析及平稳性能评价
3.1 车辆受风载大小的主要影响因素
分析两种风载模型在横风激扰作用下单轨车辆的动力响应情况,由式(3)~(5)可知,车辆受风载大小的主要影响因素为车速、风速和合成风向角,且横风对头车影响最大,故可对头车进行动力响应分析,进而评价整车动力响应及运行平稳性.
模拟单轨车辆在不同工况下的运行情况,即不同车速、风速和合成风向角的单轨车辆车体质心处横向加速度的时域历程曲线,轨道线型为直线轨道(长度L=500 m)[14].为便于研究车辆的横向振动,在单轨车辆动力响应分析及平稳性能评价中未考虑轨道不平顺.
3.2 平稳性能评价分析
目前,国内外尚未制定专用于跨座式单轨车辆的平稳性评价标准,因此,借鉴GB/T 5599-1985《铁道车辆动力学性能评定和试验鉴定规范》,基于仿真获取的单轨车辆横向加速度振动响应时程曲线进行数值计算[15-16].平稳性指标W采用斯佩林平稳性指标的计算方法,即
上式中:ai为振动加速度,m·s-2;fi为振动频率,Hz;F(fi)为频率修正系数.

表3 客运轨道车辆平稳性评价Tab.3 Stability evaluation of passenger rail vehicles
当含有h个频率成分时,平稳性指标计算式为
按上述标准,计算各控制变量下的单轨车辆平稳性指标.参考GB 5599-1985《铁道车辆动力学性能评定和试验鉴定规范》的客运轨道车辆平稳性评价,如表3所示.
3.3 合成风向角对车体质心处横向加速度的影响
设置仿真时间为20 s,步长为0.02,瞬态中国帽风载模型和非定常随机风载模型的风速均为u=15 m·s-1,合成风向角分别为45°,60°,75°,90°,105°,120°,135°,单轨车辆以60 km·h-1的速度稳定运行,在t1时刻分别驶入横向风带,车体质心处的横向加速度,如图5所示.
由图5可知:在两种风载模型中,当合成风向角为90°时,横向加速度最大;当合成风向角为135°时,横向加速度最小;当合成风向角为90°,75°时,横向加速度明显增大,说明角度不同,其等效风速也不同,车辆受到的风载相差较大;当合成风向角为75°~90°时,等效风速变化较大,横风对车辆安全性能有显著影响.
3.4 车速对车体质心处横向加速度的影响
设置仿真时间为20 s,步长为0.02,单轨车辆开始分别以10,20,30,40,50,60,70,80 km·h-1的稳定速度运行,t1时刻驶入风速u=15 m·s-1的横风风带后离开,因合成风向角为90°时的等效风速最大,故后续研究的合成风向角均设置为90°.车速对车体质心处横向加速度的影响,如图6所示.
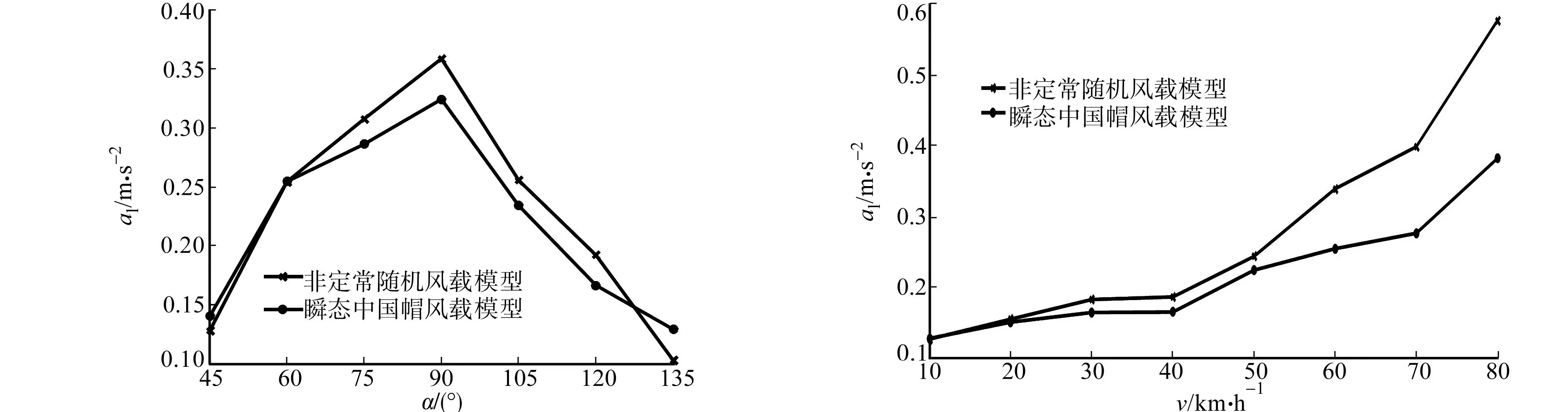
图5 合成风向角对车体质心处横向加速度的影响 图6 车速对车体质心处横向加速度的影响 Fig.5 Effect of synthetic wind direction angle on Fig.6 Effect of vehicle speed on lateral accelerationlateral acceleration at mass center of car body at mass center of car body
由图6可知:车体质心处横向加速度的最大值整体上随车速的增大而增大;由于抖振力和自激力的存在,相较于瞬态中国帽风载,非定常随机风载使单轨车辆的速度增幅更为明显,当车速增加至60~80 km·h-1时,非定常随机风载作用效果更为明显,横向振动响应强烈.
根据仿真得到单轨车辆在两种风载模型下的时域历程曲线,将其导入Matlab进行计算,从而评价其运行的平稳性.当横风风速为15 m·s-1时,单轨车辆在直线段轨道上以10,20,30,40,50,60,70,80 km·h-1的车速行驶.在非定常随机风载模型中,单轨车辆以10~50 km·h-1的速度行驶,车体横向平稳性指标均未超过2.50,车辆平稳性较好;以60,70,80 km·h-1的速度行驶,车体横向平稳性指标分别为2.750 9,3.050 7,3.645 0,均不能满足车辆平稳运行的要求.在瞬态中国帽风载模型中,单轨车辆以10~60 km·h-1的速度行驶,车辆平稳性较好;以70,80 km·h-1的速度行驶,车体横向平稳性指标分别为2.584 2,3.048 9,均超过2.50,单轨车辆无法平稳行驶.

图7 风速对车体质心处横向加速度的影响Fig.7 Effect of wind speed on lateral acceleration at mass center of car body
3.5 风速对车体质心处横向加速度的影响
当两种横向风速分别为5,10,15,20 m·s-1,合成风向角均为90°时,作用于车速为60 km·h-1的单轨车辆,其风速对车体质心处横向加速度的影响,如图7所示.
由图7可知:车辆横向加速度受风速的影响显著,随着风速的增加,横向加速度增大;当风速从15 m·s-1增至20 m·s-1时,相较于瞬态中国帽风载,非定常风载作用下车辆横向加速度折线更陡,对风速作用效果也更为敏感.
当车辆在直线段轨道上以60 km·h-1的车速行驶时,在风速为15,20 m·s-1的非定常随机风载和风速为20 m·s-1的瞬态中国帽风载的作用下,车体横向平稳性指标分别为2.750 9,2.961 3,2.704 8,可相应地评为合格、合格和良.此时,单轨车辆应立刻减速甚至停运,以保证运行平稳性.其余各种工况评价结果均为优,可安全稳定运行.
4 横风激扰下跨座式单轨车辆运行的安全区域
跨座式单轨车辆以不同的车速分别通过瞬态中国帽风载模型、非定常随机风载模型,根据国家标准GB 5599-1985《铁道车辆动力学性能评定和试验鉴定规范》计算限值下的临界安全风速,进而基于这两条线的交点及最内侧部分确定安全区域与危险区域的分界线,依据该线可得到某车速下对应的安全运行所不能逾越的风速,从而得到横风激扰下单轨车辆运行安全域,当合成风向角为75°~90°时,等效风速变化较大,故所有风载均垂直于车体.
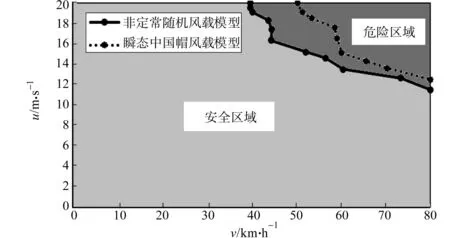
图8 单轨车辆运行的安全区域与危险区域Fig.8 Safe and dangerous areas for monorail vehicles
当车辆速度为0~80 km·h-1,平均侧风速度为0~20 m·s-1时,单轨车辆运行安全区域与危险区域,如图8所示.
由图8可知:随着车辆运行速度的增加,车辆允许的临界安全风速降低.非定常随机风载模型曲线表示所有敏感条件的阈值界限集合,是安全区域与危险区域的边界.当风速为12.65 m·s-1时,车辆临界速度约为73.4 km·h-1;而若要保持车辆以车速80 km·h-1匀速行驶在轨道梁上,则标准高度风速检测应限制在11.5 m·s-1左右.非定常随机风载曲线右上区域为危险区域,表明跨座式单轨交通应关闭或使用风屏障等措施以保证行车安全.从风载模型来看,非定常随机风载模型的临界风速大于瞬态中国帽风载模型,非定常随机风载模型考虑了侧风下车辆所受的抖振力和自激力.因此,在进行安全评估时,应选择非定常随机风载曲线的左下区域.
5 结论
1) 车速、风速、合成风向角对横风下单轨车辆的运行平稳性有着极大的影响,随着车速、风速的增大,单轨车辆运行平稳性越差;而当合成风向角为75°~90°时,车辆所受等效作用力最大,有脱轨可能.
2) 相较于瞬态中国帽风载模型,非定常随机风载模型使单轨车辆的横向振动响应更为明显.当风速为15 m·s-1,车速增加至60 km·h-1时,瞬态中国帽风载模型的车辆速度达到70 km·h-1,车辆的横向振动响应过大,超过平稳性指标.
3) 给出横风激扰下单轨车辆运行安全区域,非定常随机风载曲线表示所有敏感条件的阈值界限集合,是安全区域与危险区域的边界.在安全区域中,车辆可稳定行驶;在危险区域中,跨座式单轨车辆应采取立即减速、就近停车等措施,以保证行车安全.
