由圆周角例题谈解题策略
2020-06-01赵丹
初中生世界·九年级 2020年5期
赵丹

圆自身的旋转不变性让圆中的计算呈现灵活多样性,圆中的角度、半径问题是中考考查的热点。由于圆周角、圆心角、弧度数之间的关系,再加上弦、弧、角之间的灵活转化,为角的计算提供了不同方法。本文从有关圆中角的计算问题出发,在不同图形中结合条件寻找不同的解题方法,优化圆中角的计算。
一、借助圆的轴对称性(垂径定理)
例1 如图1,AD是半圆的直径,点C是[BD]的中点,∠ADC=55°,则∠BAD是多少?
【解析】由点C是[BD]的中点,联想到垂径定理,连接OC、BD可得OC⊥BD。方法1:借助等腰△COD,可得∠OCD=55°;由OC⊥BD,得∠CBD=35°,则问题解决。方法2:借助圆内接四边形对角互补,求得∠ABC=125°,可得∠CBD=∠CDB=35°,∠ADB=20°,可得∠BAD=70°。
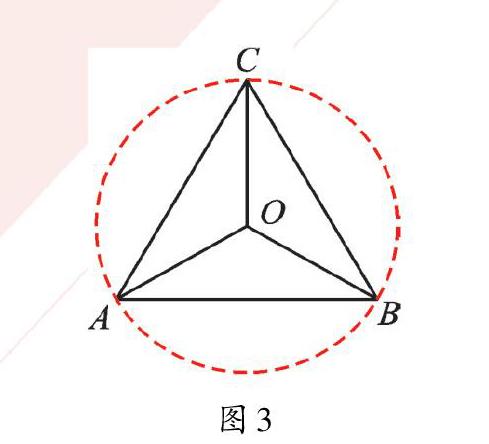
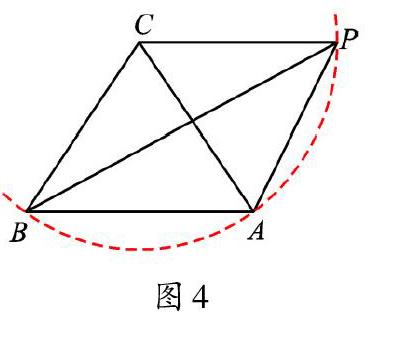
【解析】看到CA=CB=CP,联想到定长;由∠ACB=70°,联想到定角。看到定长定角问题,我们便联想到圆,可以看作是以C为圆心,以CA长为半径的圆,直接可得∠APB=35°。
【点评】在几何图形中,寻找隐圆是解决问题的一种非常简便的策略,一旦看到了隐圆的存在,许多问题便能快速解决。这就需要我们在解题过程中注重对隐圆模型的识别,从题目中挖掘定长、定角条件,以不变应万变。
圆中角的计算方法很多,如何做到解题方法的优化,这需要平时不断积累,做題时善于思考,不仅要追求正确,还要灵活运用不同方法,借助一题多解发展思维。
(作者单位:江苏省南京市科利华中学棠城分校)
