追本溯源：数学问题探究的一般方法

王磊

中考复习时，我们要重视对教材中的典型问题的深度探究。许多中考题的基本图形、基本思想、基本策略，都源自对教材中的问题的进一步整合和挖掘。下面就以苏科版教材八（下）第145页第11题为例，说说如何追本溯源。

原题再现

从反比例函数图像上的任意一点分别向两条坐标轴作垂线，这两条垂线与坐标轴所围成的矩形的面积不变。为什么？

【解析】根据题意，可以作图分析。如图1，点A在反比例函数y=[kx]上，坐标是（m，n），从点A向x轴和y轴作垂线，与两条坐标轴围成的矩形的面积是S=[mn]。而反比例函数的解析式可变形为xy=k，所以mn=k，也就是说[mn]是个定值，所以矩形的面积是不变的。

拓展一 通过面积求反比例函数的系数

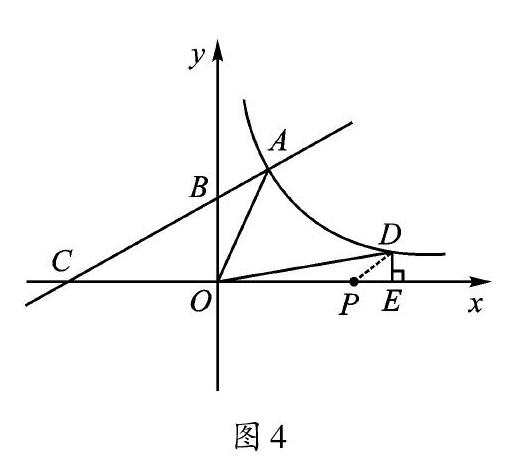
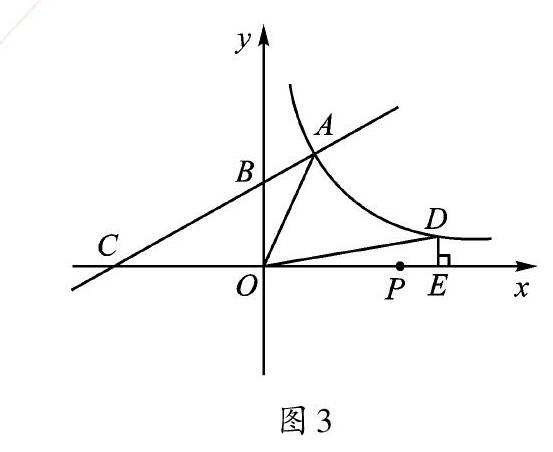
如图2，已知A为反比例函数y=[kx]（x<0）的图像上一点，过点A作AB⊥y轴，垂足为B。若△OAB的面积为2，则k的值为（）。

【点评】本题通过面积法，求反比例函数的系数k。与矩形面积不同的是，我們需要把横、纵坐标的积的绝对值除以2，才能得到三角形的面积，与教材例题相比，是逆向运用。

拓展二 反比例函数的综合题

【点评】利用坐标乘积的不变性，求交点坐标，是反比例函数与一次函数整合的常见题型，准确地求出交点坐标是关键。通过图形的几何性质，得到数量关系，利用设未知数解方程的方法，就可以很好地解决问题了。

（作者单位：江苏省连云港市海州实验中学）