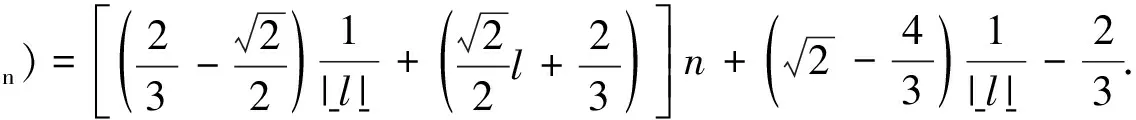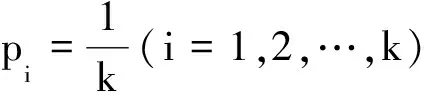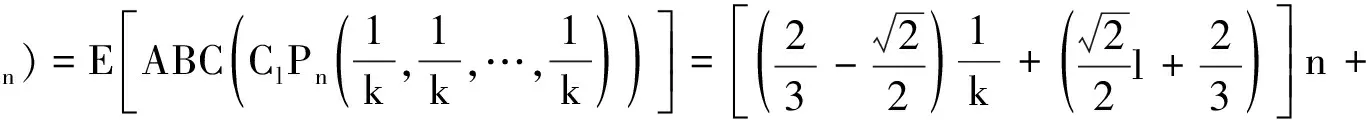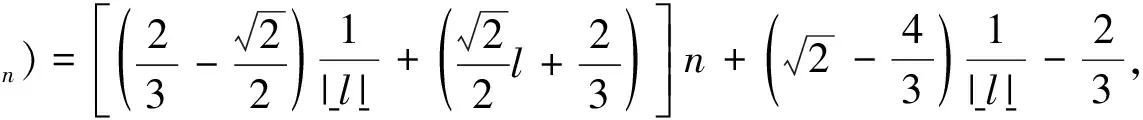随机多边形网格链图的ABC指数
2020-06-01陈维楠魏首柳杨世永郑升
陈维楠, 魏首柳, 杨世永, 郑升
( 闽江学院 数学与数据科学学院, 福建 福州 350108 )
0 引言
1947年,H.Wiener[1]首次提出了分子拓扑指数(Wiener指数).因分子拓扑指数对研究有机化合物的定量结构-性质相关性(QSPR)和定量结构-活性相关性(QSAR)具有重要作用,所以受到国内外学者的广泛关注,并得到了进一步发展,如Randic指数、Wiener指数、Merrifield-Simmons指数、Harmonic指数、代数-几何指数、Zagreb指数、扩展Zagreb指数和原子键连通性指数,等等[2].1998年, Estrada等[3]首次提出了原子键连通性指数(简称ABC指数),该指数是一个关于分子图的拓扑不变量,其定义为
(1)
其中G表示一个包含顶点集V(G)={v1,v2,…,vn}和边集E(G)的图(或分子图),di表示其顶点vi的度数.在研究烷烃等化合物的热形成过程中,因ABC指数可作为一个有效的预测性指数,因此其在烷烃的稳定性以及环烷烃的应变能等研究中得到了广泛应用[3-4].近年来,许多国内外学者研究了多种特殊图类ABC指数的计算问题.例如:文献[5-6]研究了不同特征或有条件限制的树的ABC指数以及它们的各种数学性质;林文水等[7]证明了Gutman提出的关于极小ABC指数的树的猜想;文献[8-9]对具有给定度序列图的ABC指数问题进行了研究;文献[10-11]对双圈图和化学双圈图的ABC指数进行了研究;文献[12-13]刻画了具有极值ABC指数的树状六边形网格图的极图及其构成;陈锦松等[14]建立了一个图的移边变换与ABC指数的关系公式; Ke[15]研究了苯环系统和荧蒽系统在自由边界条件下的ABC指数的表达式,并且给出了具有极大和极小ABC指数的树状苯环系统;文献[16]研究了8.8.4格子图和8.8.6格子图在自由边界条件下的ABC指数.文献[17]研究了柱面、轮胎曲面、克莱因瓶和莫不乌斯带上的四边形网格图的ABC指数,并得到了其精确表达式;武琳等[18]研究了图的ABC指数与直径之间的关系;文献[19-20]用差分方程和递归等方法分别研究了随机五边形网格链图、六边形网格链图和螺旋六边形网格链图的ABC指数的数学期望表达式.基于上述研究,本文利用类似文献[19-20]的方法研究一般随机多边形网格链图的ABC指数.
1 基本定义
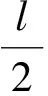

图1 n=1,2时的唯一多边形链图
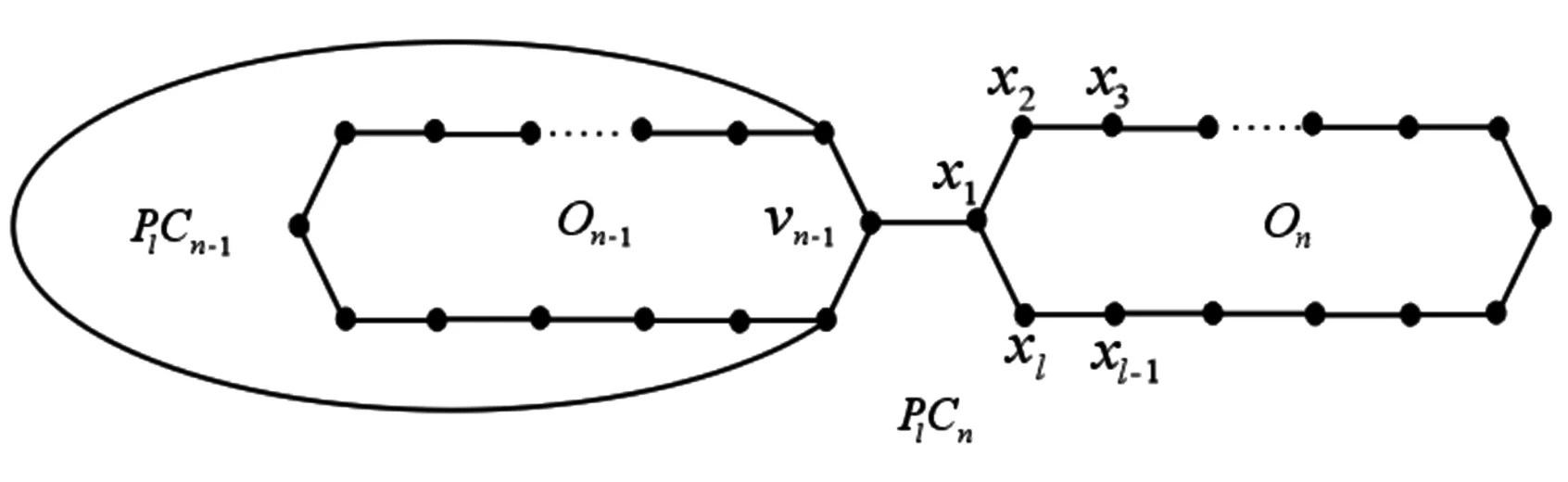
图2 长度为n的l多边形链图PlCn
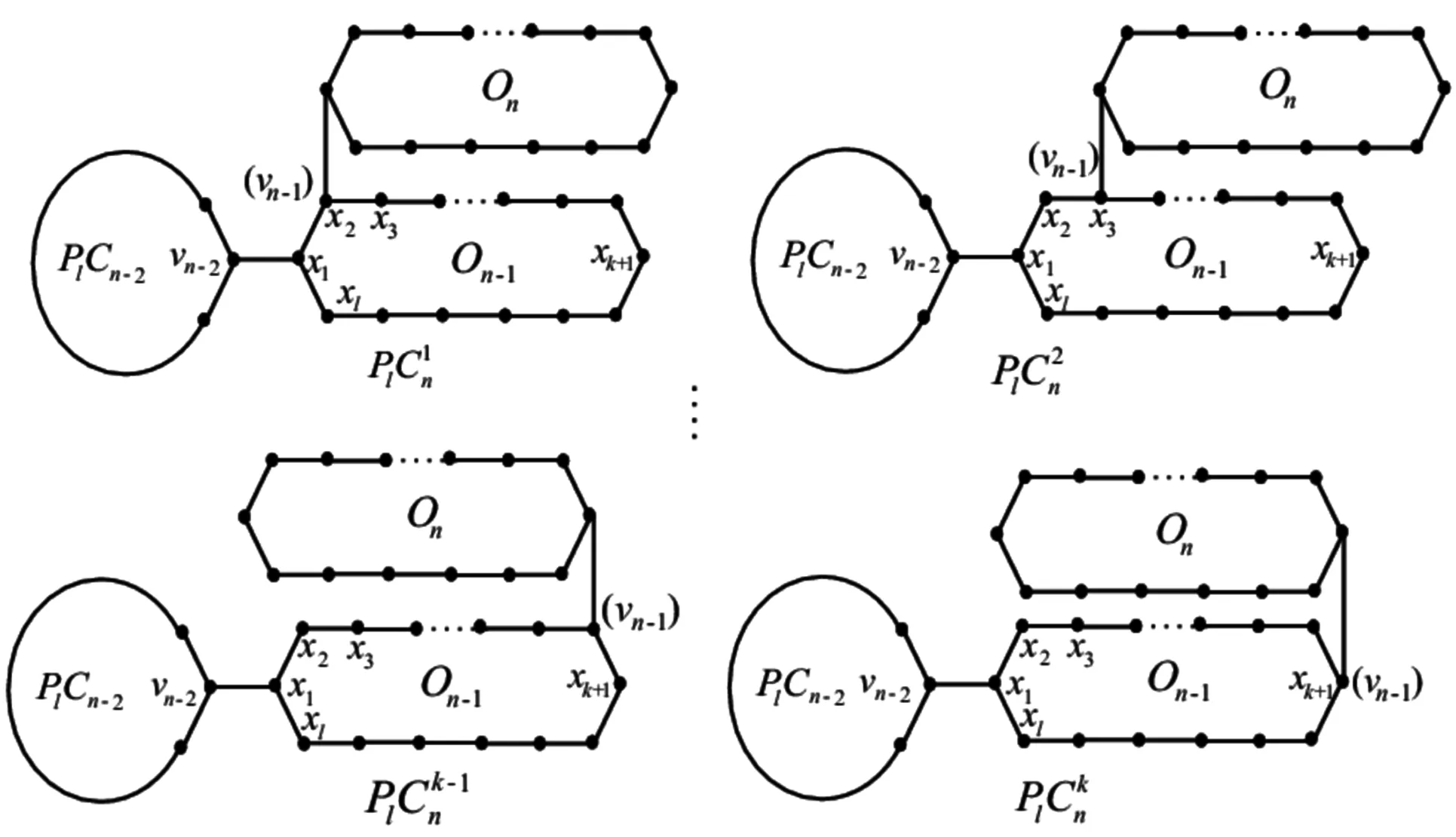
图3 一般的l多边形链图的k种连接方式
对于n≥3, 假设概率pi(1≤i≤k)都是常数且与n无关,则上述描述的过程是一个马尔可夫链过程.关联概率后的l-多边形链称作随机l-多边形链,且记作PlCn(p1,p2,…,pk).
2 随机多边形网格链图的ABC指数
为了推导方便,继续沿用上述的相关符号和定义.如果图G中一条边的2个顶点的度分别为i和j,则称此边为图G的(i,j)- 边,用nij(G)表示其边数.如图2所示,假设PlCn是在一个长为n-1的l-多边形链图PlCn -1上联接一个外部的新l-多边形On而得到的一个长为n的l-多边形链图,其中On=x1x2…xl.由l-多边形链图的定义可知,PlCn只有(2,2)- 边、(2,3)- 边和(3,3)- 边.所以,公式(1)可以转化为
(2)
由公式(2)可知,只需要确定PlCn的3类边的数目n22(PlCn)、n23(PlCn)和n33(PlCn), 然后将其代入公式(2)即可计算出l-多边形链图PlCn的ABC指数.
因PlCn(p1,p2,…,pk)是一个长度为n的随机l-多边形链图,所以ABC(PlCn(p1,p2,…,pk))是一个随机变量,本文用En=E[ABC(PlCn(p1,p2,…,pk))]表示其数学期望.
定理1设PlCn(p1,p2,…,pk)是一个长度为n的随机l-多边形链图(n≥2),则
当n≥3时,由图3所示的非同构联接方式可得出n22(PlCn),n23(PlCn)和n33(PlCn).
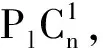
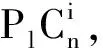
由上述2种情形的结果可得:
即
(3)
注意到E[En]=En, 将其应用于方程(3)可得如下递归式:
(4)
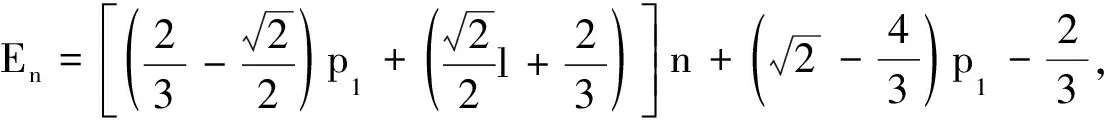
3 多边形网格链图ABC指数的平均值
设SlCn是由n个l-多边形网格链图构成的一个集合,定义SlCn的所有l-多边形网格链图的ABC指数的平均值为
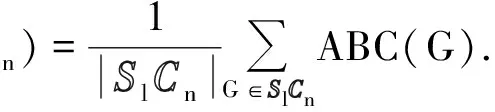
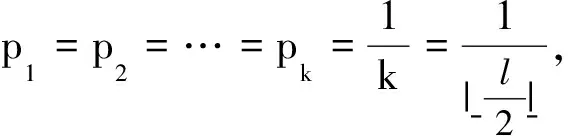
定理2SlCn中所有元素的ABC指数的平均值为