基于JC法的地震作用下土坡动力可靠度分析

2020-06-01罗浩，李逸，郑博，邹琦

北方交通 2020年4期

罗浩，李逸，郑博，邹琦

（中国市政工程中南设计研究总院有限公司武汉市 430010）

0 引言

地震、火山和滑坡被列为全球性三大地质灾害。滑坡常常给工农业生产以及人民生命财产造成巨大损失，有的甚至是毁灭性的灾难。自然界中大部分滑坡都是由地震引发的。地震作用下的边坡稳定性研究，对生产建设乃至人类的生存环境具有十分重大的意义。

然而，地震作用下的边坡稳定性分析一直是岩土工程界的难点问题。目前地震作用下的边坡稳定性研究的主要方法有拟静力法、Newmark分析法、动力有限元时程分析法以及完全动力分析法，且主要是对边坡的安全系数进行求解。传统拟静力法求解边坡安全系数的方法比较粗糙，吕擎峰等对其做了改进［1］，然而拟静力法没有考虑地震的动力特性，在评价岩土边坡稳定性方面还需进一步发展与改进。Newmark分析法［2］指出堤坝稳定与否取决于地震时引起的变形，并非最小安全系数，为地震作用下边坡的稳定性分析带来了新思路，然而它无法给出地震作用下的边坡破坏标准，给实际工程应用造成不便。动力有限元时程分析法［3］以及完全动力分析法［4-5］可以得到地震作用下边坡的安全系数时程曲线，更加直观地反应边坡的安全状态。康永君提出以动力有限元时程分析得到应力场，再使用遗传算法搜索每个时刻下的临界滑裂面，进而确定其安全系数，从而得到边坡在动力作用下的安全系数时程曲线［6］；刘汉龙提出了用最小平均安全系数作为评价指标，并利用安全系数最大振幅的0.65倍作为平均振幅来反映安全系数随地震波动变化的过程［7］。

地震作用下的边坡安全系数能在一定程度上反应地震作用下边坡的安全性，然而边坡的土性参数具有随机性［8］，单凭某一特定状态下的参数求得的安全系数并不能全面反应地震作用下边坡的安全状态。娄国充对地震作用下土质边坡的可靠度进行了分析［9］，但该论文是建立在拟静力方法的基础上的，具有一定的局限性。考虑土体参数的随机性，运用完全动力分析法，对地震作用下的边坡进行可靠度分析。

1 地震作用下土坡的动力计算模型及响应

1.1 地震作用下土坡的动力计算模型

在建立地震作用下土坡的运动方程时进行了两点假设：

（1）土体为各向同性的粘弹性体。

（2）土体在任一水平面上的剪应力是均匀分布的。地震作用下土坡的稳定性分析为平面应变问题。

设H0为坡高，θ为坡角，ugx、ugy分别为水平、垂直地震动。建立地震作用下土坡的动力计算模型，如图1所示。

对土体进行受力分析，考虑粘滞阻尼，得到地震干扰下土体作强迫振动的动力平衡条件为［10］：

X方向：

Y方向：

其中ux、uy分别为水平、垂直方向土体的位移，G为土的剪切模量，E为土的弹性模量，ρ为土的密度，cs为土的阻尼系数。

地震作用时土坡动力计算模型的边界条件为：

1.2 土坡的地震响应

设边坡底部基岩的输入水平地震动为ugx＝Im（Ux0eiat），垂直方向为ugy＝Im（Uy0eiat）［11］。其中Ux0和Uy0为水平垂直两方向的地震动位移幅值，a为地震动频率。

则由式（1）得水平位移为：

其中

由式（2）得竖向位移为：

其中

2 地震作用下土坡的可靠度分析

2.1 土中任意点的应力状态

在土体中取一单元体，设作用在该单元体上的静大、小主应力分别为σs1和σs3，动大小主应力分别为σd1和σd3，与大主应力作用面成任意角α的平面上的静正应力和静剪应力分别为σs和τs，动正应力和动剪应力分别为σd和τd。则单元体上的大小主应力σ1、σ3以及与大主应力作用面成任意角α的平面上的正应力σ和剪应力τ分别为相应静应力和动应力的叠加。如图2所示。

静力作用下，正静应力静剪应力为：

动力作用下，正动应力和动剪应力为：

其中ax和ay为土体的水平和垂直运动加速度。

则得正应力和剪应力为：

2.2 动力极限状态方程

采用整体圆弧滑动法求解边坡的安全系数，如图3所示，设坡角为θ，滑动圆弧为L，圆心坐标为O（x0，y0），半径为r，滑动体的重量为W，滑动体重心至圆心的水平距离为d。滑弧圆心位置按4.5H0经验法确定，图示中β1和β2可以查相应表格得到［12］。

则边坡的安全系数表达式如下：

其中

工程一般要求Ks≥1.2，本文取Ks＝1.2为临界状态。由此可得到极限状态方程为：

即

2.3 土坡的动力可靠度计算

选取土体重度γ、粘聚力c和内摩擦角φ为基本变量，采用JC法求解土坡的动力可靠度。设P*（γ*，c*，φ*）T为极限状态面上的一点，即：

在点P*处将式（25）按Taylor级数展开并取至一次项，有

则结构的可靠指标

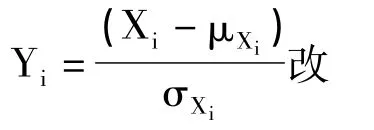
在原始X空间中的坐标为

由于验算点未知，不能直接求解β，故通过迭代法求解。

3 算例

3.1 概况

武汉地区某残积土坡的断面形式如图4所示，地震设防烈度为7度，设计基本地震加速度值为0.10g，竖向加速度分量取水平加速度分量的1／2，作用10s。依据有关试验资料进行统计，边坡有关参数按近似正态分布的统计特征值见表1［13］。

表1 土体材料力学参数

3.2 位移地震响应分析

如图5所示，选取坡顶点A和坡顶点垂直向下4.5m处的B点进行地震响应分析。AB两点水平和垂直方向上的地震响应的计算结果如图6和图7所示。

由图可见，AB两点位移随着时间呈明显的波动现象，在静力平衡位置作往返运动。A点最大垂直位移为0.01823m，B点最大垂直位移为0.00492m。可见坡体垂直位移在竖直方向随高程增加而增大。垂直方向的位移响应与输入的地震波一样呈现着正弦波动，土体阻尼作用不明显。

A点最大水平位移为0.05602m，B点最大水平位移为0.03362m。水平位移地震响应具有明显的竖向放大效应，且水平位移地震响应要远大于垂直位移地震响应，这是由于重力作用减弱了地震响应。水平位移地震响应表现出较明显的位移累积效应。

3.3 土坡的失效概率与可靠度时程

取β1为25°、β2为35°，运用离散元强度折减法计算得到该土坡地震前的安全系数为1.47，地震作用下的安全系数为0.96。可见，地震作用下土坡安全系数明显降低。

运用拟静力法计算得到失效概率为0.3037，可靠度为0.6963。运用动力方法计算可得到失效概率和可靠度的时程曲线如图8和图9所示。

由图可看出地震作用下的土坡失效概率和可靠度时程曲线呈现衰减的趋势，随着时间的推移而逐步趋向稳定。地震作用下土坡的失效概率的范围是［0.2118，0.5086］，均值为0.3618。可靠度的范围是［0.4914，0.7882］，均值为0.6382，即动力可靠度为0.6382。可见本方法求得的失效概率要大于拟静力法的结果，这是因为拟静力法没能考虑到地震特性和土体的动力特性，表明动力分析方法较拟静力法分析地震作用下土坡的稳定性更可靠。