产业集聚的要素配置效应再检验
——来自安徽28个两位数制造业的证据
2020-05-31刘冬萍
刘冬萍
(合肥师范学院 经济与管理学院,安徽 合肥 230001)
1 理论梳理与研究假设
1.1 理论梳理
国内外学者对产业集聚的生产要素配置效应研究已经比较充分,相继出现集聚规模经济论、生产要素拥挤论、集聚生命周期论三种不同的观点.
集聚经济理论:规模经济效应 该理论认为产业集聚促进了劳动力、资本、技术以及市场环境等生产要素的集中和优化,形成了内部规模经济从而降低企业生产成本.[1-3]同时,还产生了知识外溢和技术外溢等外部规模经济,不断带来经济体内创新产出和技术进步,提高了要素配置效率(劳动生产率),促进集聚区的经济增长.
国内有关产业集聚对生产要素配置和经济增长影响的研究起步较晚,多是对国外有关理论的延伸和实证检验,并且认为产业集聚对生产要素配置效率有正向影响. 如范剑勇利用2004年我国276个城市数据,实证发现非农产业集聚对劳动生产率具有显著的促进作用[4];刘修岩基于2003—2006年我国211个地级市的面板数据,通过工具变量法研究发现,就业密度、专业化水平等集聚因素对非农劳动生产率有显著正向影响[5];张治栋等运用安徽省县域面板数据,也得到了集聚能显著促进工业增长的结论[6].
集聚不经济理论:拥挤效应 该理论认为随着行业在一定程度上集聚,同类企业对劳动力、资本等生产要素的需求快速增加,造成要素价格上涨,生产成本上升;另一方面,同类企业的高度集聚还会带来过度竞争,造成低利润或负利润等不经济现象.[7-9]同时,集聚区基础设施、自然环境的承载力是有限的,过度集聚也会造成难以承载等问题,如交通拥堵、环境污染、生态破坏.
随着我国东部沿海集聚区内劳动力成本上涨、交通拥挤、过度竞争等问题的出现,国内学者发现各集聚区在获取了规模经济的同时,也产生了各种形式的集聚不经济. 如王缉慈等通过对沿海地区外向型产业集群的分析发现,产业集聚过程中出现了“逐底竞争”的无序现象[10];唐根年等研究发现部分制造业呈现聚集过度、生产要素拥挤的现象,生产要素配置效率存在损失[11];胡浩然等也验证了拥挤效应的存在[12-14].
集聚生命周期理论:适度规模 该理论认为在集聚早期,规模经济效应远大于拥挤效应. 随着集聚的加深,拥挤效应不断增大. 在规模经济效应和拥挤效应达到动态平衡时,集聚的总效应在某地区达到最高(拐点),之后过度集聚便会出现阻碍生产要素有效配置的现象.[15-17]
近年来,国内学者开始对我国产业集聚的适度规模和最优集聚度问题进行了探索性研究. 周圣强等利用面板数据门限回归法实证分析了产业集聚与全要素生产率的倒“U”型关系,并测算了“拐点”,但并未考虑资源能源消耗、环境污染等因素[18];潘雅茹等研究发现区位熵低于1.45时,产业集聚会对全要素能源效率有显著正向影响;高于1.45时,则会抑制全要素能源效率的提升,二者现存在稳健倒“U”形关系[19];李骏等验证了产业集聚的“拐点”效应[20].
1.2 研究假设
通过梳理可以看出,规模经济论强调产业集聚对生产要素配置效率的正向促进效应,而集聚拥挤论则分析了负向阻碍效应. 相对而言,集聚生命周期论对产业集聚的正负效应及其相互作用机制进行了深入剖析,比较全面,更加符合当前实际,即产业集聚并不总是有效的,存在适度集聚规模. 当前,随着皖江承接产业转移示范区、长江经济带等国家政策的全覆盖,安徽省制造业产业集群日益增多,截止2018年底,已形成209家省级产业集群专业镇. 张晴运用安徽各地市面板数据实证验证了战略新兴集聚对区域经济竞争力有显著促进效应[21]. 然而,在取得规模经济的同时,安徽也出现了资源开发过度、污染转入等不经济现象[22]. 那么,安徽制造业集聚对生产要素配置效率的影响是否也存在“拐点”?
基于此,本文提出假设:
制造业集聚与生产要素配置效率呈倒U型关系. 当集聚规模处于较低水平时,规模经济占主导作用,集聚规模的提高有利于提升要素配置的效率,属于集聚的要素配置效应提升阶段,此时会吸引更多企业进入集聚区;规模持续扩大后,过多的企业集聚将使企业资源消耗及生产要素价格上升,逐渐超出集聚区的承受能力,出现资源成本上升等要素拥挤现象,阻碍要素的有效配置,直到完全抵消了规模经济,达到动态平衡(临界点),此时生产要素配置的效率达到最大;当集聚规模超过动态平衡时的临界点之后,要素拥挤带来的效率降低占据主体,进入要素配置的效率下降阶段.
2 模型构建与变量说明
2.1 模型构建
本研究借鉴周圣强和朱卫平的方法[18],以全要素生产率来衡量生产要素的配置效率[21],建立制造业集聚的要素配置效应模型为
TFPjt=β0+β1·Aggjt+γ∑Xjt+μj+εjt
(1)
其中,t代表时期,j代表行业,TFPjt为行业的全要素劳动生产率(基数为1);Aggjt为产业集聚指数,考虑到单一测度指标的局限性,本研究分别将地理集聚指数(EGjt)、区位熵(LQjt)和空间基尼系数(Gjt)纳入模型中进行检验;Xjt为其他控制变量,μj表示个体效应,εjt为随机干扰项. 为了提高模型的准确性,对全要素劳动生产率及控制变量取对数,以降低样本离散程度. 同时,考虑到产业集聚对全要素生产率的非线性影响,在模型中依次加入产业集聚的二次项、三次项,修正模型为
(2)
针对该模型,本文首先采用静态面板固定效应估计进行检验,然后运用动态面板(系统GMM)方法再次进行估计,旨在通过不同估计方法,对结果的一致性进行评估. 其中,静态面板估计中的个体效应能够得到有效体现,但可能存在内生性问题,系统GMM则以滞后一期项为工具变量,能很好的解决内生性问题.
2.2 变量说明
2.2.1 全要素劳动生产率(TFPj)本文以全要素生产率(TFP)作为衡量劳动生产率的指标,采用基于产出的非参数数据包络分析-马奎斯特指数法(DEA-Malmquist)来测度各行业全要素生产率(TFP)的变化情况.j行业的全要素生产率指数计算公式为
(3)
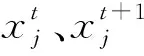
距离函数Dc、Dv恰好为数据包络分析法(DEA)中CCR模型和BCC模型中最优值的导数. 因此,可利用DEA方法求解出ΔTFPj指数. 本文利用Deap2.1软件进行DEA-Malmquist测算. 产出指标为产值,采用各行业规模以上工业总产值衡量,并用工业生产者出厂价格指数平减得到各行业剔除价格因素后的实际值. 投入指标为资本和劳动力,其中劳动力投入采用制造业各行业全部从业人员年平均人数来衡量;资本投入采用制造业各行业固定资产投资合计来衡量,并用固定资产投资价格指数进行平减处理. 需要说明的是,由于Malmquist指数法测算的指标并不是各年的当量,而是相对于上一年的变化. 因此,为了便于实证检验,以基年全要素生产率为基数,设定为1,则以后各年TFPj为上年的全要素生产率乘以当年的ΔTFP.
2.2.2 集聚程度(EG、LQ、G)本研究分别采用行业地理集聚指数(EGjt)、行业区位熵(LQjt)和行业空间基尼系数(Gjt)作为关键解释变量,来检验制造业集聚对全要素生产率的影响.
假设某地区有m个地市、n个产业,则j产业的EG指数计算公式为
(4)
其中,EGjt代表j产业的EG指数;sijt为t时期i市j产业的规模占该产业总规模的比重,xit表示t时期i市所有行业总规模占该地区总规模的比重.Hjt为t时期该地区j产业企业规模分布的赫芬达尔指数,采用关爱萍等的替代性办法[23]测算,即
(5)
其中,ouputijt为t时期产业j在i市的产值,ouputjt为t时期产业j在全省的总产值,kijt为t时期产业j在i市的企业单位数.
行业区位熵(LQjt)与各地区制造业专业化水平不同,但计算方式类似,即
(6)
其中,j表示行业,Pjt、TPjt分别表示安徽省和全国t时期j行业的总产值;Pt表示t时期安徽省制造业总产值;TPt表示t时期全国的工业总产值,LQjt表示相对于全国来说,t时期j行业的集聚专业化水平.
行业的空间基尼系数(Gjt)计算公式为
(7)
其中,Sijt代表i地区j行业t时期产值占全省该行业比重,xit表示i地区产值占全省总产值的比重.Gjt为安徽省j行业t时期的基尼系数,取值介于0~1,值越大,表示该行业在地理上的集聚程度越高,即产业在地理上愈加集中.
2.2.3 其他控制变量1)市场化水平(MLjt) 用各行业总产值减去国有控股工业企业产值后与该行业总产值之比来衡量. 2)外商投资企业产出占比(Fjt) 用各行业外商投资企业产值占该行业总产值的比重衡量. 3)企业平均规模(ASj) 采用各行业总产值与规模以上企业数之比来衡量,产值采用工业生产者出厂价格指数(以2010年为基年,记为100)平减.
2.3 数据来源与描述统计
本研究采用2010—2017年安徽28个两位数制造业行业面板数据作为样本. 考虑到2012年行业分类体系的变化,将之前的橡胶制品业与塑料制品业合并为橡胶与塑料制品业,将之后的汽车制造业和船舶、航空航天及其他运输制造业合并为交通运输制造业. 安徽省各行业产值、行业企业数、行业全部从业人员平均人数、固定资产投资额等数据均来源于2011—2018年的《安徽统计年鉴》. 其中,2018年的安徽统计年鉴中,缺少2017年各行业产值数据,以主营业务收入代替. 另外,在计算集聚指数时,16个市分行业产值、企业数及从业人员数数据则来自于各地市的统计年鉴. 《2016年阜阳统计年鉴》缺失,以同年安徽省指标值减去其他地市该指标值来替代. 各类货币量指标均按照2010年的不变价格进行了平减以消除物价因素. 各变量原始数据的描述性指标见表1.
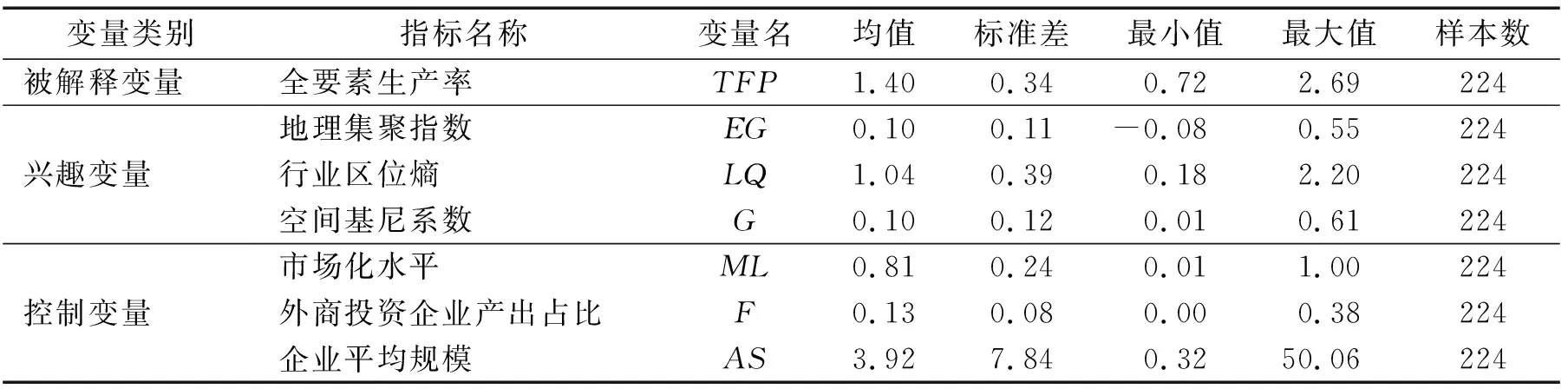
表1 相关变量的描述性统计
3 实证研究:产业集聚的要素配置效应检验
3.1 变量的平稳性检验
本文所使用的面板数据T为8,N为28,是典型的短面板数据,但因为要进行动态面板估计,为了避免出现伪回归的现象,对模型中的面板数据采用单位根(ADF)进行平稳性检验(结果见表2). 各变量的ADF检验统计量均显著,不存在单位根,均为平稳面板序列.
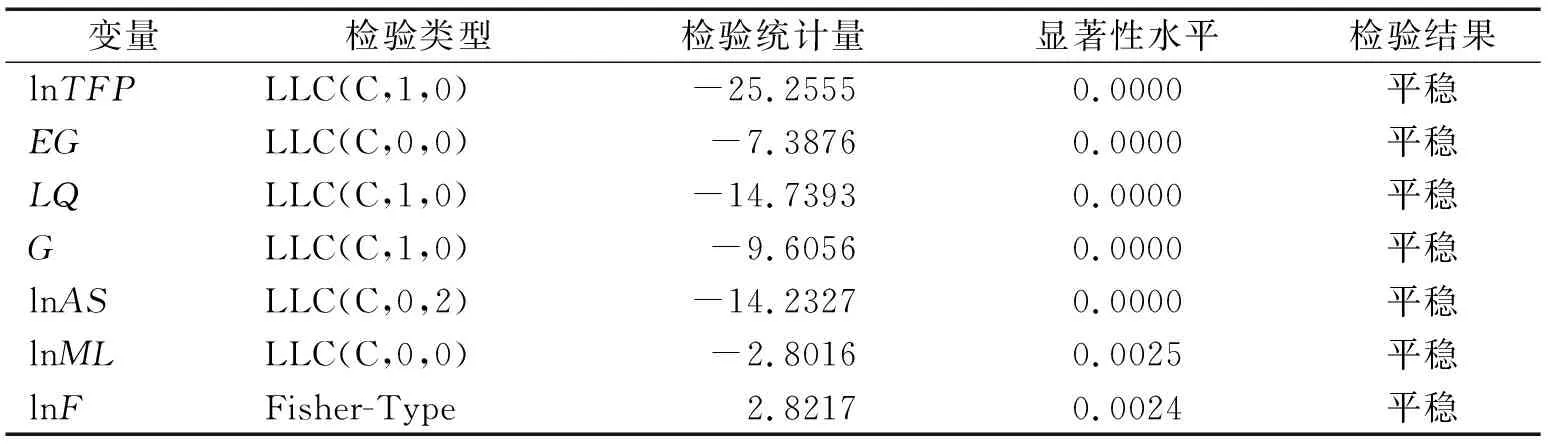
表2 ADF检验结果
注:检验类型中的LLC(C.T.K)中C表示截距项,T表示时间趋势项,K表示滞后阶数项;lnF部分数据缺失,为非平衡面板,故用Fisher单位根检验.
3.2 模型估计结果
表3为静态面板固定效应模型的估计结果,表4为动态系统GMM模型的估计结果,系统GMM估计以自变量的滞后项为工具变量,能很好地避免内生性问题. 由模型1、模型2、模型7和模型8的估计结果可以看出,地理集聚指数(EG)的一次项对全要素劳动生产率(lnTFP)有显著影响,且估计系数为正,但其二次方项(EG^2)对全要素劳动生产率的影响并不显著,表明地理集聚指数与全要素劳动生产率之间呈正向线性关系,并非倒U型关系,反映了安徽省制造业地理集聚有利于提高生产要素配置效率;由模型3、模型4、模型9和模型10的估计结果可以看出区位熵(LQ)及其二次方项(LQ^2)对全要素劳动生产率均有显著影响,且二次方项的估计系数为负,表明行业区位熵与行业全要素劳动生产率之间呈显著的倒U型关系;由模型5和模型6的估计结果可以看出空间基尼系数(G)及其二次方项(G^2)对全要素劳动生产率的影响均不显著,考虑可能存在内生性问题,而模型11和模型12采用系统矩估计方法,在解决内生性问题的前提下,空间基尼系数一次项的估计系数显著为正,二次项估计系数仍不显著,表明空间基尼系数与全要素劳动生产率有正向线性关系.

表3 全要素生产率(lnTFP)影响因素的静态面板固定效应模型
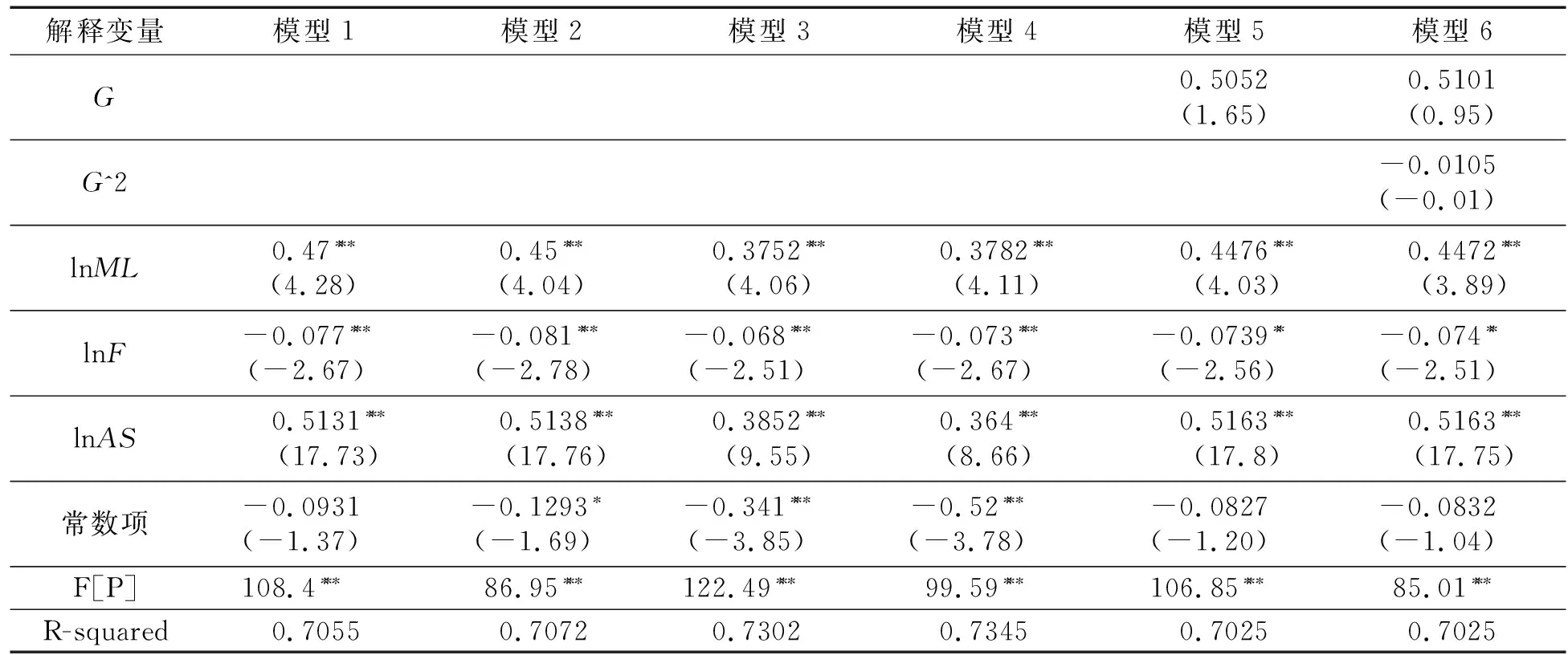
续表3
注:* 、* * 、* * * 分别表示0.1、0.05、0.01的显著性水平下显著.
总体来说,以行业地理集聚指数(EG)、行业空间基尼系数(G)为表征的产业集聚,其要素配置效应均体现出促进作用,并没有出现先“扬”后“抑”的倒U型特征. 以行业区位熵(LQ)为表征的产业集聚,与行业全要素劳动生产率呈现显著的倒U型关系. 具体来说,根据模型10,行业区位熵的一次项(EG)和二次方项的估计系数均在 1%的水平上显著,符号分别为正和负,即当行业区位熵水平低于拐点值(2.04)时,集聚对全要素劳动生产率会产生促进作用. 表明当行业专业化水平不高时,集聚带来的生产规模扩张,使得企业能够共享基础设施、降低运输成本,实现集聚的规模经济效应;当高于拐点值(2.04)时,过多的企业集聚一方面会引起同类企业的过度竞争,另一方面会使得生产要素价格上升,逐渐超出集聚区的承受能力,出现要素拥挤现象,阻碍要素的有效配置. 但从安徽各行业的区位熵水平来看,2010—2017年,28个制造业224个样本中,仅有电气机械和器材制造业的6个样本的区位熵水平超过拐点值,其余均小于拐点水平,反映了安徽省制造业的行业专业化水平普遍偏低,对行业全要素生产率总体上仍然是促进作用,抑制作用尚不明显. 总体来说,目前安徽省制造业集聚对生产要素配置效应总体上呈现出促进作用,未来一段时间内安徽应进一步促进制造业的集聚发展.
另外,由表4中的模型7至模型9结果可知,行业全要素劳动生产率具有显著的时间滞后效应,前一期的劳动生产率对后一期的有显著正向影响,即当前劳动生产率较高的行业,其未来的劳动生产率就可能持续走高,即行业全要素劳动生产率有明显的路径依赖特征.
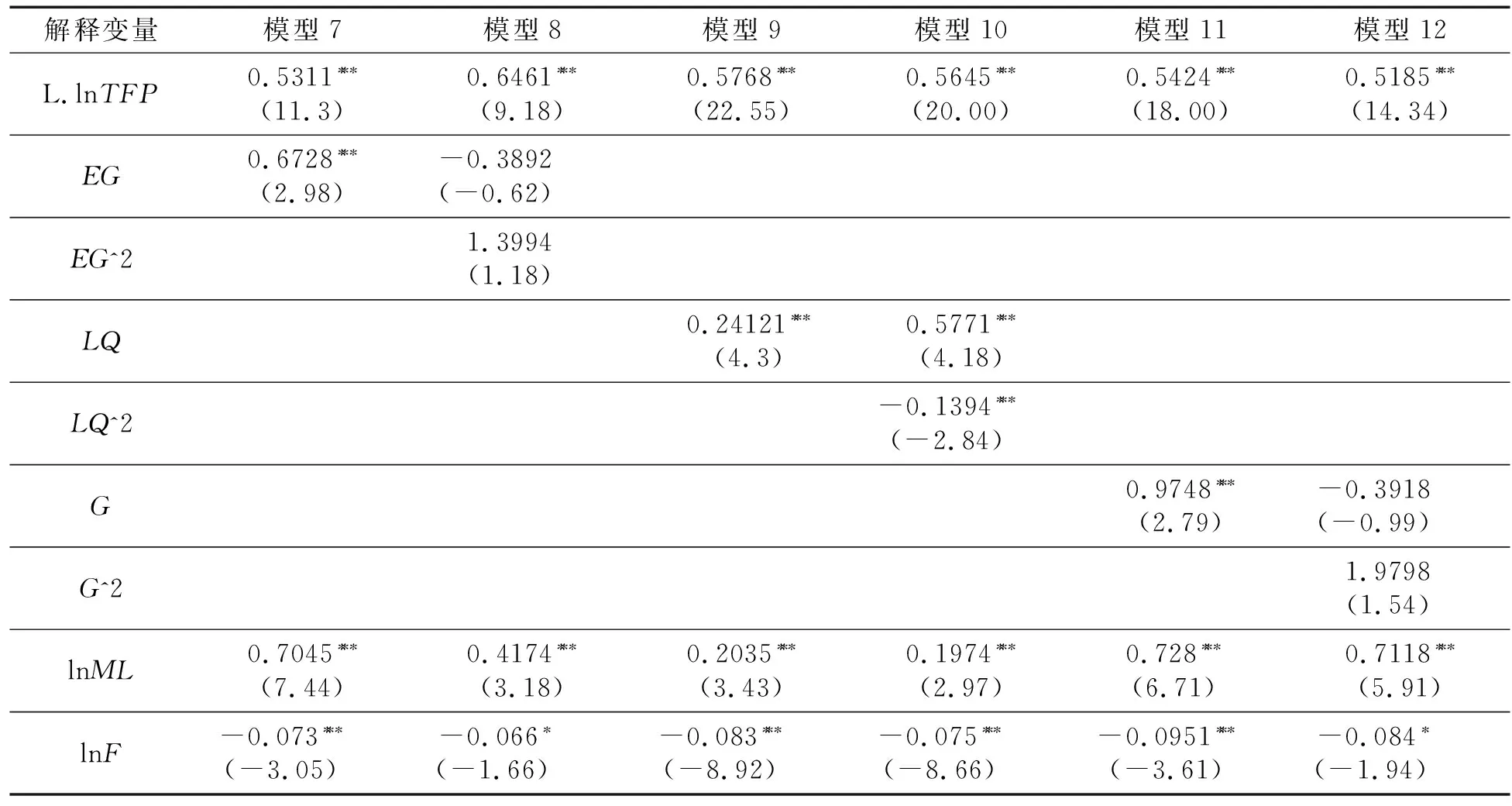
表4 全要素生产率(lnTFP)影响因素的动态系统GMM模型

续表4
最后,模型1至模型12中,各控制变量对全要素生产率的影响均在不同水平下显著. 其中,市场化水平(lnML)的估计系数均显著为正,与预期结果一致,表明市场化水平越高的行业,其全要素劳动生产率也越高;企业平均规模(lnAs)的估计系数均显著为正,表明企业平均规模越高的行业,其劳动生产率也越高,从另一个角度反映了规模化生产能提高生产效率;外资企业产出占比(lnF)的估计系数均显著为负,表明外资企业产出占比越高的行业,其全要素劳动生产率越低,与苏楠等研究结论[24]相似,这可能是由于地方政府为了引进外资而给予过多优惠政策,阻碍了市场对资源的有效配置.
4 结论与建议
本文以安徽28个两位数制造业为例,实证检验了产业集聚的要素配置效应. 发现:1)以行业地理集聚指数、行业空间基尼系数为表征的产业集聚,要素配置效应均主要体现出促进作用,并没有出现先“扬”后“抑”的倒U型特征;2)以行业区位熵为表征的产业集聚,与行业全要素劳动生产率呈现显著的倒U型关系,当行业区位熵水平低于拐点值时,集聚对全要素劳动生产率会产生促进作用;3)从各行业的区位熵水平来看,仅有电气机械和器材制造业的区位熵水平超过拐点值,其余均小于拐点水平,反映出安徽省制造业的行业专业化水平普遍偏低,对行业全要素生产率总体上仍然是促进作用,抑制作用尚不明显.
综上所述,安徽省制造业集聚对生产要素的配置总体上呈现出积极地促进作用,未来一段时间内应进一步促进制造业的集聚发展,特别是专业化集聚水平. 具体来说:1)各级地方政府在承接产业转移、促进产业升级过程中应充分考虑资源优势,引导有利于形成专业化特色的行业优先集聚,同时在提供完善政策的基础上,由市场机制来引导企业的集聚与扩散行为,从而提高生产要素的配置效率;2)以合肥、芜湖为中心,积极促进计算机、通信、汽车、航空航天设备等先进制造业的高端化发展,提升自主创新能力,为承接长三角地区高新技术产业转移奠定好技术基础;3)针对宿州、阜阳、淮北等制造业欠发达的皖北地区,进一步提升和促进农副食品加工业、食品制造业等具有区位优势的制造业集聚,同时加大对交通运输、物流配送、通讯、网络等基础设施等的建设力度,营造开放、公平公正的商业氛围,为省内制造业合理、有序的转入做好“软硬件”准备.
