上钢下混组合桩水平承载性能影响因素分析

2020-05-31苏晓栋孟星宇陈灿明

水利与建筑工程学报 2020年2期

苏晓栋,李致,孟星宇,吴烨,陈灿明

(1.南京水利科学研究院，江苏南京 210029；2.水利部水科学与水工程重点实验室，江苏南京 210029)

钢管桩和PHC桩或预制的预应力钢筋混凝土桩是高桩码头最常用的桩型[1-2]。钢管桩因其强度高和抗弯性能优异，但工程造价相对较高，常用于自由长度大或水平荷载较大的高桩码头；而PHC桩或预制的预应力钢筋混凝土桩工程造价明显低于钢管桩，但因其强度和抗弯性能明显低于钢管桩，一般用于以竖向承载为主或桩基自由长度和水平荷载相对较小的高桩码头。为了在确保桩基抗弯性能的前提下降低工程造价和改善沉桩性能，工程中衍生出钢管桩和PHC管桩的组合桩，其中上部钢管桩下部PHC桩的组合桩(简称上钢下混组合桩)能在确保抗弯性能不变的条件下有效降低工程造价[3-4]，而上部PHC桩下部钢管桩的组合桩(简称上混下钢组合桩)能在不减小桩基竖向承载力时极大提升桩基的沉桩性能[5-7]。目前组合桩已在工程中得到一定的运用，但缺乏规范系统的理论体系指导，对组合桩的承载机理及影响因素等缺乏规律性认识[8-9]。本文采用ABAQUS有限元软件计算分析对上钢下混组合桩(见图1)的接桩部位埋深、桩径、连接段参数对水平承载性能的影响，提出上钢下混组合桩承载力的计算方法与设计建议，为上钢下混组合桩的推广运用提供依据。

图1 上钢下混组合桩示意图

1 模型参数选择

1.1 计算模型

上钢下混组合桩模型桩径D为1.0 m，总桩长55.0 m，桩身入土深度35.0 m，自由长度20.0 m，PHC桩壁厚130 mm，钢管桩壁厚16 mm，联接段长度0.50 m，通过焊接将钢管节及加劲板与PHC管桩联接成一个整体。采用三维实体有限元模型，联接段加劲肋简化为等刚度满圆周布置，桩身各部分之间为固接。PHC桩下部为全封闭式桩尖，不考虑土塞效应。模型水平方向桩周土体直径取25倍桩径(25D)，土层总厚度取1.5倍桩基入土深度[10]。有限元模型网格采用渐变网格，土体由顶部至底部网格高度从0.5 m～1.5 m，桩周环向由圆心至圆周网格长度从0.1 m～2.0 m，土体范围内每隔2.0 m划分一个单元。桩体和土体的单元均采用三维八节点减缩积分单元(C3D8R)[11]。上钢下混组合桩三维有限元模型见图2。有限元模型坐标系以泥面处桩轴心为坐标系原点，泥面为XY平面，基桩轴线向上为Z轴正方向，水平荷载沿X轴正方向通过桩截面圆心。模型边界采用底部边界设置固定约束，四周边界设置法向水平位移约束[12-13]。

1.2 计算参数

钢管桩和PHC桩均采用线弹性本构模型，钢管桩及联接段均为Q345钢，PHC桩为A型桩，混凝土强度等级C80。地基土体采用Mohr-Coulomb弹塑性本构模型，以淤泥质粉质黏土作为土体模型参数。模型材料物理力学参数见表1。水平荷载逐级施加于桩顶横截面中心点。

图2 上钢下混组合桩三维有限元模型

表1 上钢下混组合桩模型材料物理力学参数

1.3 加载方式

根据《水运工程地基基础试验检测技术规程》[14](JTS 237—2017)中有关桩基水平静荷载试验的规定，加载分级进行，加载时每级级差取预计最大荷载1/10。根据钢管桩试桩资料，预估水平极限荷载为200 kN，因此每级荷载取20 kN[15-16]。

2 接桩深度影响

对于上钢下混组合桩，钢管桩越长越安全可靠，但工程造价越高。因此选择合适的钢管桩长度至关重要。根据纯钢管桩模型计算结果，钢管桩在极限荷载作用下弯矩零点位于泥面以下12D左右(D为桩径，接桩深度定义为PHC桩桩顶至泥面距离)，因此选择接桩深度Zs为0D、2D、4D、6D、8D、10D、12D总计7种上钢下混组合桩与纯钢管桩模型进行计算，以分析接桩位置对组合桩水平承载性能的影响。

2.1 桩身弯矩

对不同接桩深度上钢下混组合桩分级施加水平荷载至200 kN。180 kN荷载时各接桩位置组合桩桩身弯矩曲线见图3，桩身弯矩零点位置(插值法计算)见图4。

计算结果表明：

(1) 不同接桩深度组合桩在各荷载级作用下，其桩身弯矩分布规律与纯钢管桩基本相同。

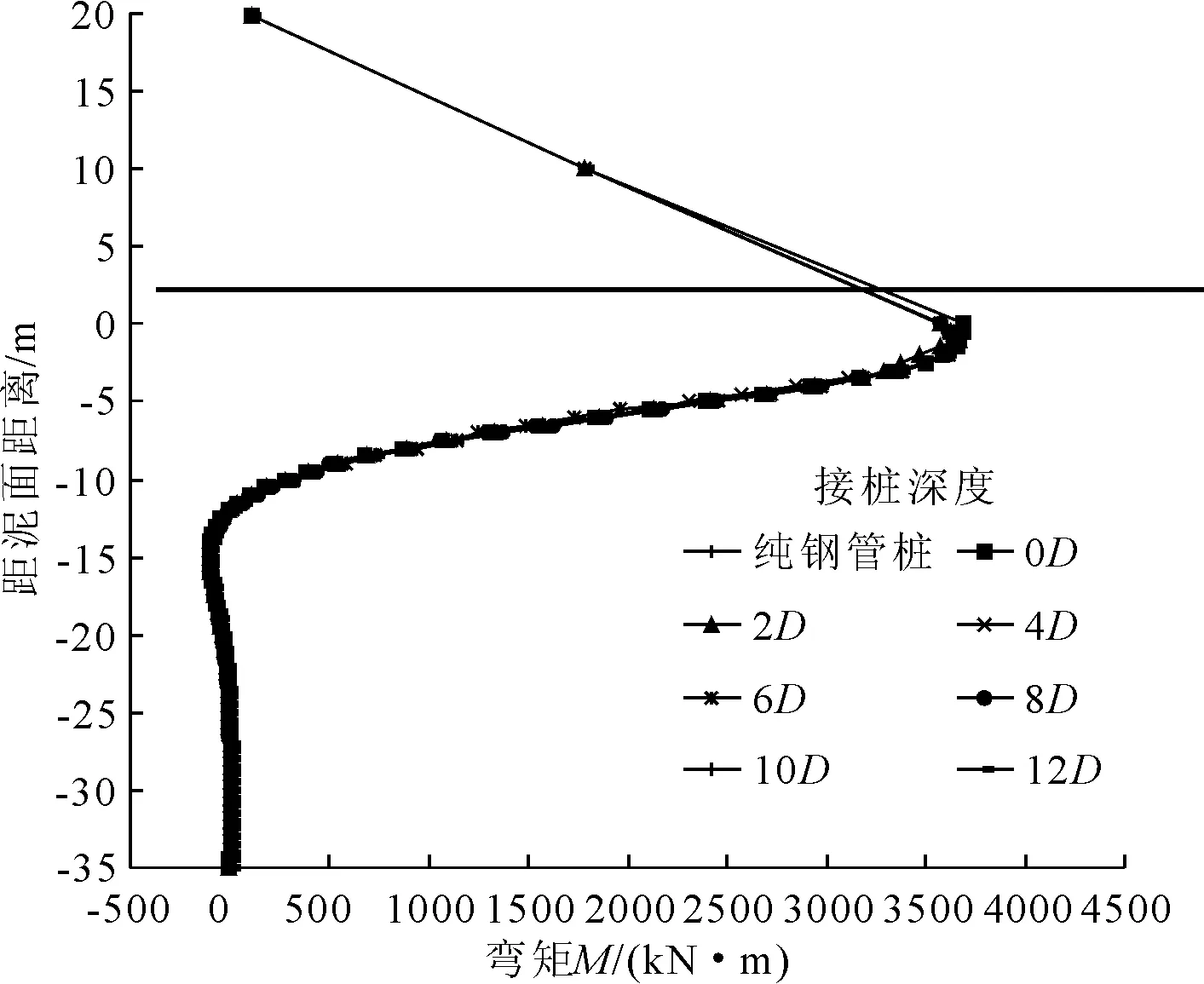
图3 180 kN荷载组合桩桩身弯矩

图4 接桩深度对桩身弯矩零点位置影响曲线

(2) 相同荷载作用下不同接桩深度组合桩的桩身最大弯矩值与位置均与纯钢管桩相近，桩身最大弯矩相差不超过0.89%。当接桩深度为0D时，位置相差最大为0.63D；接桩深度为2D～8D时最大弯矩位置相差不超过0.05D。较大荷载级时桩身最大弯矩一般在泥面以下0.90D～1.05D位置处。

(3) 钢管桩和组合桩在各水平级作用下的弯矩零点位置在-10.0D～-12.5D之间，且弯矩零点位置随着荷载的增加而逐渐下移。接桩深度对桩身弯矩零点位置的影响幅度在0.00D～0.26D左右(相对于纯钢管桩)。

因此，上钢下混组合桩的接桩深度对桩身弯矩分布影响较小，设计时可直接参考纯钢管桩桩身弯矩计算结果。

2.2 桩身泥面处位移

归一化的组合桩接桩深度与泥面处水平位移关系曲线见图5，图中横坐标Zs/D为接桩深度与桩径之比，纵坐标U/Us为组合桩泥面处水平位移U与同条件纯钢管桩泥面处水平位移Us之比。

计算结果表明：

(1) 相同荷载作用时组合桩泥面处位移均略小于纯钢管桩，且随荷载增加差距逐步加大。受联接段刚度的影响，接桩深度2D～4D时，组合桩泥面处水平位移最小。当接桩深度大于8D时，组合桩泥面处水平位移趋于稳定。

(2) 由于联接段的刚度明显大于钢管桩，当其位于受力较大区域时(最大弯矩附近)，对泥面处水平位移的减小程度较大，当联接段位于受力较小区域并逐渐下移时，其对水平位移的影响也逐步减小，直至无影响。

(3) 接桩深度4D时桩身泥面处水平位移的影响最大，在接近极限荷载180 kN时组合桩桩身泥面处水平位移比纯钢管桩小5.38%，而同条件下接桩深度大于8D时，组合桩桩身泥面处水平位移比纯钢管桩小2.16%。

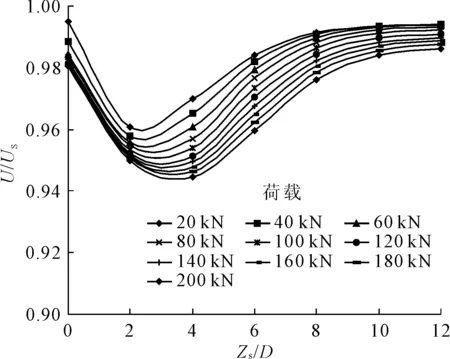
图5 归一化的接桩深度-泥面处水平位移关系

2.3 桩身应力

以钢管桩桩身应力达到或接近允许最大应力值的水平荷载级(180 kN)为例，比较纯钢管桩和组合桩桩身应力分布特点，钢管桩和联接段竖向应力(S33)云图见图6和图7(图中数值为拉正压负)。

计算结果显示：

(1) 在180 kN荷载作用下纯钢管桩桩身最大压应力310.4 MPa，最大拉应力306.6 MPa。

(2) 接桩深度0D组合桩钢管段桩身最大拉应力282.9 MPa，最大压应力290.3 MPa，小于纯钢管桩7.73%、6.48%，接桩深度2D组合桩钢管段桩身最大拉应力299.5 MPa略小于纯钢管桩，最大压应力317.3 MPa略大于纯钢管桩，幅度2.32%～2.22%；而接桩深度4D～12D组合桩，其桩身最大拉应力值306.5 MPa～307.0 MPa，最大压应力值为309.8 MPa～310.2 MPa，与纯钢管桩相近(幅度小于0.19%)。

(3) 随着接桩深度由0D增大至12D，下部PHC段桩身应力迅速降低，最大拉应力由54.34 MPa降至1.39 MPa，最大压应力由52.85 MPa降至1.67 MPa。

(4) 组合桩联接段刚度大于钢管桩，其最大应力均小于钢管桩段。

图6 水平荷载180 kN时钢管桩和组合桩桩身应力云图(单位：Pa)

图7 180 kN水平荷载时组合桩联接段应力云图(单位：Pa)

2.4 极限水平承载力

上钢下混组合桩水平极限承载力以钢管桩和PHC管桩桩身受力达到材料设计强度为依据。纯钢管桩和组合桩水平极限承载力见表2。

根据计算结果，组合桩水平极限承载力受接桩深度变化的影响很大。接桩深度小于8D时，组合桩的水平极限承载力主要受PHC桩的抗弯性能控制，当接桩深度大于等于8D时，组合桩水平极限承载力由钢管桩的抗弯性能确定，组合桩联接段刚度相对较大，不影响组合桩总体承载性能。

表2 不同接桩部位距泥面深度的组合桩水平极限承载力

因此，选择恰当的接桩深度是影响上钢下混组合桩水平承载力的最主要因素，组合桩接桩深度组合合适，其水平极限承载力将与纯钢管桩基本相同。

3 桩径影响

在计算分析组合桩接桩深度对承载性能影响规律的基础上，进一步探究桩径对组合桩极限承载力的影响。分别建立桩径600 mm、700 mm、800 mm、1 000 mm、1 200 mm、1 300 mm、1 400 mm的上钢下混组合桩模型，钢管桩壁厚12 mm～20 mm，PHC桩壁厚110 mm～150 mm，分别取接桩深度为5.5 m、6.0 m、6.5 m、8.0 m、9.0 m、10.0 m、10.5 m。预估桩基水平极限承载力60 kN～450 kN，荷载分10级逐步施加。

桩径对组合桩桩身弯矩零点位置影响曲线见图8(a)，不同桩径组合桩在各级水平荷载作用下桩身泥面处水平位移见图8(b)，各桩径组合桩水平极限承载力见图8(c)。不同桩径的纯钢管桩和组合桩钢管段桩身最大拉压应力值见表3。

图8 不同桩径的组合桩水平承载性能

表3 不同桩径的纯钢管桩和组合桩钢管段最大拉压应力

注：表中纯钢管桩联接段的最大拉压应力是指同条件的组合桩联接段所在位置对应的纯钢管桩的应力。

根据计算结果分析：

(1) 在极限荷载时，不同桩径的组合桩桩身弯矩曲线、桩身应力分布和泥面处水平位移曲线与纯钢管桩基本一致。

(2) 组合桩桩径越大极限荷载越大，桩身最大弯矩位置越低，且随荷载增大而逐渐下移，荷载加至极限荷载时，桩径600 mm、1 000 mm和1 400 mm组合桩最大弯矩点分别位于泥面下0.30D、1.02D和1.43D处。

(3) 极限荷载作用下组合桩弯矩零点随桩径增大逐渐下移。各级荷载作用下，桩径600 mm、1 000 mm和1 400 mm组合桩桩身弯矩零点分别位于泥面下11.10D～14.41D、10.43D～12.36D和10.20D～11.93D处。

(4) 各桩径组合桩桩身泥面处的水平位移均略小于同桩径的纯钢管桩，桩径600 mm～1 200 mm时减小幅度不大于3.16%，桩径1 300 mm～1 400 mm时，减小幅度不大于1.30%。

(5) 不同桩径组合桩在各级荷载作用下钢管段桩身最大拉压应力与同条件钢管桩基本一致，联接段的最大拉压应力均小于同条件对应位置的钢管桩桩身最大拉压应力，拉应力最大降低幅度28%，压应力降低幅度1.2%。

(6) 在合适的接桩深度条件下，不同桩径组合桩水平极限承载力与纯钢管桩相近，组合桩与相应桩径钢管桩水平极限承载力比值Hsc/Hs为0.998～1.003。

4 联接段参数影响

4.1 联接段长度

以桩径1.00 m的组合桩为对象，选取0.00 m、0.25 m、0.50 m、0.75 m、1.00 m、1.25 m、1.50 m、1.75 m和2.00 m共8个联接段长度，接桩深度8.0 m，分析比较联接段长度对组合桩水平受力特性的影响。

归一化的联接段长度-桩身弯矩零点关系、归一化后的连接段长度与泥面处水平位移曲线、各联接段长度组合桩水平极限承载力见图9。不同联接段长度的组合桩桩身最大拉压应力见表4。

计算结果表明：

(1) 联接段长度对组合桩内力分布影响不大，相同荷载作用下，桩身最大弯矩值的影响一般不大于0.25%，最大弯矩位置差距不大于0.10D，弯矩零点位置差距不大于0.92D。

(2) 联接段长度对桩身水平位移影响相对较大，由于联接段刚度大于钢管桩，组合桩桩身泥面处水平位移随着联接段长度增加而有所降低，接近极限荷载时，联接段0.50 m和2.00 m时，水平位移比同条件钢管桩下降2.4%和9.0%。

(3) 联接段长度变化对组合桩钢管段的最大拉压应力基本无影响，联接段最大拉压应力值随着联接段长度的增加而增加，最大拉应力值为61.2 MPa～140.4 MPa，最大压应力值为72.6 MPa～165.3 MPa，均小于相应的钢管桩段的桩身最大应力。

(4) 联接段长度对组合桩水平极限承载力有一定影响，但影响程度不大。当接桩深度8D、联接段长度0.00 m～1.25 m的组合桩水平极限承载力受钢管桩控制，承载力与纯钢管桩基本相当。当联接段长度超过1.50 m时，组合桩水平极限承载力将由钢管桩控制转变为受PHC管桩控制，此时组合桩水平极限承载力低于纯钢管桩，联接段长度1.5 m和2.0 m时组合桩承载力分别下降0.2%和1.6%。

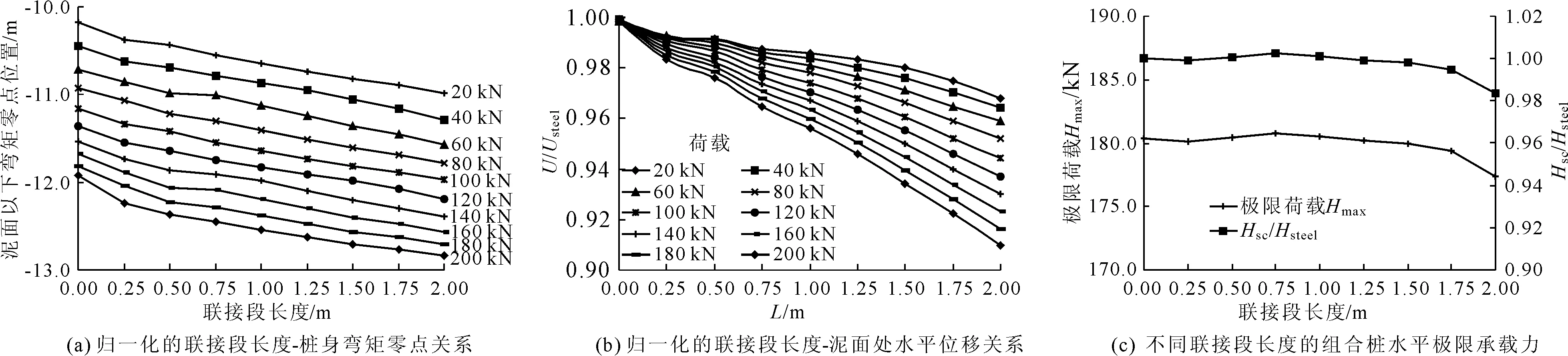
图9 不同联接段长度的组合桩水平承载性能

表4 不同联接段长度的组合桩桩身最大拉压应力

4.2 联接段刚度

针对桩径1.0 m，接桩深度8D，联接段长度0.50 m的上钢下混组合桩，仅改变联接段刚度为0.1EI、0.5EI、1.0EI、5.0EI、10.0EI、50.0EI、100.0EI(EI为钢管桩刚度)，比较联接段刚度对组合桩受力特性的影响。

归一化的联接段刚度-桩身弯矩零点关系、连接段刚度与桩身位移曲线、连接段刚度和极限承载力影响曲线见图10。

(1) 联接段刚度对组合桩内力分布影响也不大：桩身最大弯矩值随着联接段刚度增加而略有降低，联接段刚度100.0EI时相比0.1EI桩身最大弯矩值仅降低0.12%，联接段刚度对组合桩最大弯矩值位置的影响不大于0.05D。联接段刚度在0.1EI～5.0EI时，组合桩弯矩零点位置随联接段刚度增加而逐渐下移，联接段刚度大于5.0EI时，弯矩零点位置基本不变。

(2) 联接段刚度小于1.0EI时，组合桩桩身泥面处水平位移随着联接段刚度下降而增加，联接段刚度0.1EI时比1.0EI时泥面处水平位移增加了3.59%。当联接段刚度大于1.0EI时，桩身泥面处水平位移基本不受影响。

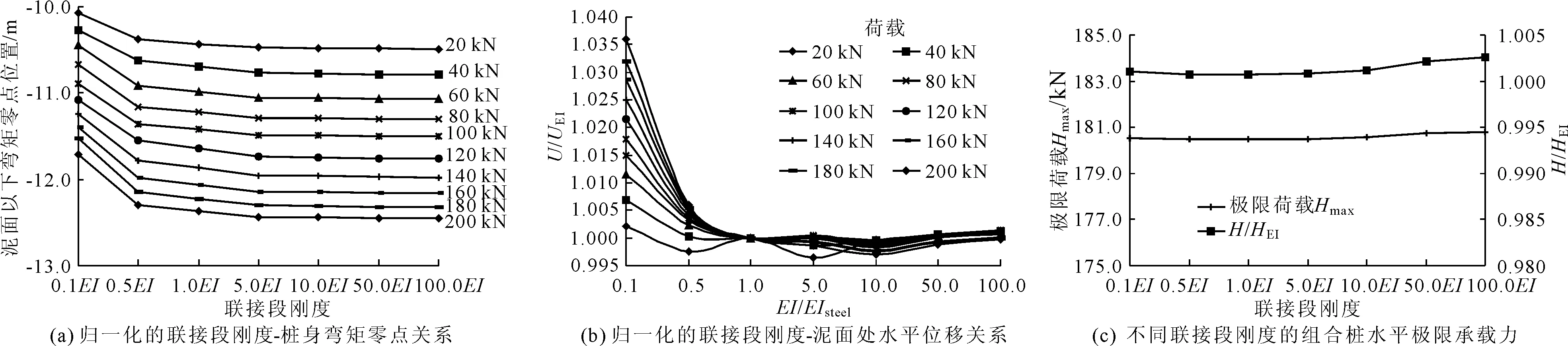
图10 不同联接段刚度的组合桩水平承载性能

(3) 联接段刚度对上钢下混组合桩上部钢管桩最大拉压应力值基本无影响，但对联接段本身最大拉压应力有一定影响，最大拉应力随着刚度的增加而增加，压应力随着刚度的增加先增加后减少。刚度小于1.0EI时，应力大于同条件钢管桩，刚度大于1.0EI应力小于同条件钢管桩。极限水平荷载作用下，联接段刚度为0.1EI的组合桩相比刚度为1.0EI的组合桩最大拉压应力值小9.13%和14.34%；联接段刚度为5.0EI～100.0EI的组合桩最大拉应力增幅为0.56%～16.24%，最大压应力变幅为1.59%～-11.09%。

(4) 组合桩水平极限承载力受联接段刚度影响较小，联接段刚度100.0EI仅1.0EI时增加0.3%，因此联接段加劲肋只需保证接桩牢固，而不必通过设置过多加劲肋来提升联接段整体刚度。