工艺参数对耐磨钢冷轧应力特性的影响
2020-05-30张玲芬
张玲芬
(烟台汽车工程职业学院,山东烟台 265500)
0 引言
耐磨钢在工业领域内有着广泛的应用[1],冷轧是其非常重要的加工方法之一[2],在制造业内受到越来越多的重视。冷轧过程中所出现残余应力问题是阻碍该工艺方案的主要因素,与工艺参数有着直接的关系,称为当前机械加工行业内的研究热点[3]。一般在冷轧过程中,轧压作用力和摩擦因数是影响耐磨钢成型效果的最关键因素,因此,在轧压工艺中,需要调节适宜的张力参数和匹配的摩擦因数,否则,在冷轧过程中容易出现边缘部位的异性变形,甚至压漏、损坏的问题[4]。
为了得出工艺参数对耐磨钢冷轧应力特性的影响,本文采用有限元数值模拟方法在不同条件下计算应力变化,为加工工艺的改进提供重要依据。
1 冷轧工艺有限元分析
1.1 数值模拟方案
有限元分析是工程分析不可或缺的方法之一,能够精确地模拟不同类型的工况以及多物理场[5],文中采用ABAQUS软件对冷轧工艺过程进行有限元分析。ABAQUS是目前应用较广泛和成熟的数值模拟软件之一,由美国HKS公司研发,在非线性材料及模型、边界调试、结构力学等方面有一定优势,在机械工程、建筑工程、水利水电、汽车制造等领域普遍得到了认可。ABAQUS具有强大的求解器,可实现不同模型的静力隐式和动力显式计算[6],集成了丰富的单元类型,能够有效地确保冷轧数值模拟分析的可靠性和精度。
1.2 建立模型装配体
冷轧工艺的模型相对简单,直接在ABAQUS/CAE内建立模型,并赋予对应的材料属性。当创建某个部件时,软件会自动生成独立的坐标系,便于在装配(Assembly)功能模块内创建最终的装配体。由于模型属于典型的大变形,因此采用显示动力学分析方法。
在装配模型构建时,首先基于转动和平动控制使得耐磨钢板模型与轧辊保持相切状态;然后在轧辊的质心位置创建1个动参考点,计算出压下率为19%时(材料极限)所需的平移位移,即可得出该动参考点的坐标;最后根据模型尺寸,设定咬入距离。
1.3 设定边界条件
冷轧分析的关键问题为接触设置,是影响计算收敛性和可靠性的主要因素。以力学角度分析,变形和接触问题属于典型的复杂非线性问题,要求确保多个物体每个时间步运动时的接触性,避免接触面之间的穿透。从数学角度分析,确保无穿透的约束方法主要有拉格朗日乘子法、罚函数法[7]和直接约束法等。根据耐磨钢的变形量,采用罚函数法。罚函数法在校验穿透时,可放大误差影响,最终使得模型不收敛,进而确保接触面的接触性,在显示动力学中非常常用。
在ABAQUS软件中,接触主要由Interaction功能模块控制。由于不同材料的接触属性不同,因此可采用罚函数(Penalty)来定义接触面之间的作用效果,包括摩擦因数。根据冷轧工艺可知,整个分析过程中不考虑托辊的变形,将其设置为刚体,采用刚体约束(Rigid Constraint)进行设置,如图1所示。
ABAQUS提供了多种单元类型供选择。根据分析类型,文中采用C3D8R(八节点线性六面体单元,减缩积分)类型的结构单元,可有效地处理非几何性的边界问题。八节点单元相比于其他单元类型,可有效地减少大变形条件下的误差。此外,八节点单元类型对于单元内的插值计算精度有着明显的作用,能够处理复杂的曲线计算。为了确保计算精度,应在计算允许条件下尽量减小网格尺寸,最终获得模型的网格划分结果如图2所示。
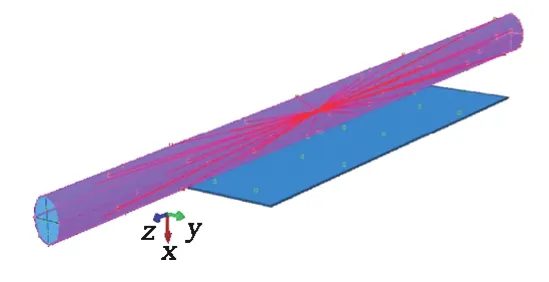
图1 刚体约束

图2 模型的网格划分结果
1.4 可视化分析
通过相应的设置,包括建立装配模型、定义材料属性、设定接触边界、提交工作界面、创建运算模型等,最终可通过连续的迭代运算获得可视化的仿真结果。图3和图4所示分别为耐磨钢板在咬入阶段、稳定阶段范围内的等效应力图。从图3、4可以看出,随着接触时间的增大,应力逐渐扩散,该分析结果可适用于不同工艺参数下的研究。
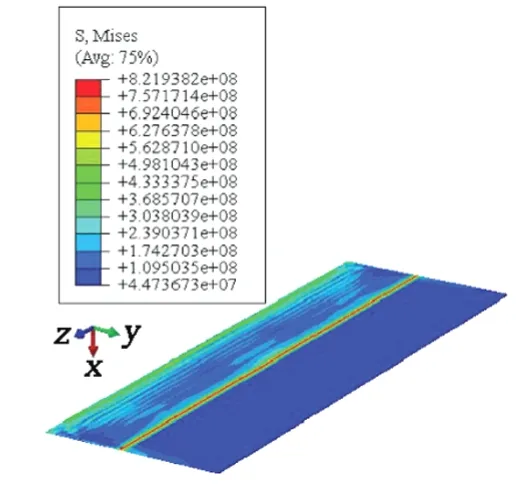
图4 稳定阶段应力云图

图3 咬入阶段应力云图
冷轧加工后的耐磨钢板表面将出现明显的残余应力。其中,外层表面为压应力,而内部表面则表现为拉应力。这种特性与金属本身的物理属性和承载有关,特别是在不同张力条件下,残余应力的大小有着显著的差别。在较大的张力条件下,残余应力将明显增大,而且波动较大。由此可见,过大的张力可直接导致塑形变形不均衡,最终引起冷轧工件的双边出现波浪形的缺陷问题。总体来看,中部位置的应力变化相对均匀,应力值相对较小,但是受钢板的厚度影响较大。
2 不同工艺参数的影响
2.1 前张力
为确保工艺参数与应力变化之间关系研究的可靠性,需采用单一变量法,即只改变某个变量进行分析。在不同前张力(95~145 MPa)条件下,可得出特定轧压方向下的应力值变化曲线,如图5所示。从图中可以看出:当前张力为95 MPa时,耐磨钢板上的最大应力值为560 MPa;应力值随着轧压距离的增大先减小更增大,在115 MPa的前张力条件下可获得更均衡和更低的残余应力。不同前张力对应力的分布变化有着明显的影响,特别是对于应力变化拐点的影响。前张力为135 MPa时,在轧压方向的最前端将出现应力变化的拐点。
2.2 后张力
保持其他参数不变,分别在后张力为45~95 MPa条件下进行计算,最终得出应力变化曲线,如图6所示。从图中可以看出:当后张力数值为45 MPa时,耐磨钢板上的最大应力为540 MPa;随着后张力的增大,应力值逐渐减小;在冷轧过程中,不同后张力条件下的残余应力差别不大。相比于前张力,后张力对应力的变化影响相对较小,比如,后张力不能明显改变应力变化的拐点,而且在远端的应力值受后张力值的影响可忽略不计。
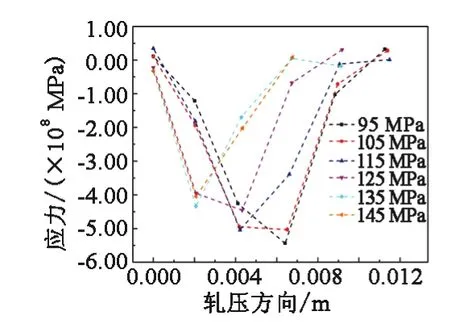
图5 不同前张力条件下的应力变化
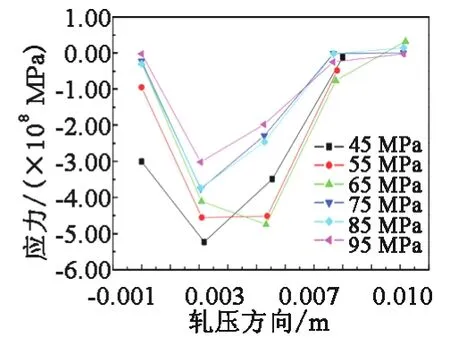
图6 不同后张力条件下的应力变化
2.3 摩擦因数
在仅改变摩擦因数(0.06~0.10) 条件下的应力变化曲线如图7所示。从图中可以看出:当摩擦因数分别为0.06和0.08时,应力值差别并不大,但是与摩擦因数为0.1时的应力值差别较大;总体来看,随着摩擦因数的增大,应力值呈增大变化趋势,这是由于接触副之间的润滑性减小,使得接触压力增大。摩擦因数在实际工程应用中也是比较容易调整的,特别是在冷轧模具的加工中,一般采用涂膜润滑材料的方法降低摩擦因数,最终达到减小残余应力的效果。

图7 不同摩擦因数条件下的应力变化
3 结束语
托辊前后张力对耐磨钢板冷轧应力的影响非常显著,这是由于前后张力明显地改变了钢板在冷轧过程中的受力情况,其法向的承载出现较大的改变。摩擦因数对冷轧压力的改变主要体现在摩擦力因素上,随着摩擦因数的增大,切向接触力增大。在实际冷轧工艺中,影响冷轧应力的因素非常多,最佳的工艺参数也难以确定,本文中基于ABAQUS的有限元仿真可以为部分工艺参数的优化提供重要的依据。
