基于Bagging改进算法变压器油中气体故障诊断研究*

2020-05-30芦佩雯黄永晶董凤珠

机电工程技术 2020年4期

芦佩雯，黄永晶，张恒，董凤珠

（1.成都纺织高等专科学校电气信息工程学院，成都 611731;2.西华大学电气与电子信息学院，成都 610039）

0 引言

变压器是发电厂和变电所的核心设备之一，对变压器故障诊断展开研究，对于降低故障发生率，提高电力系统的可靠性，具有重要的现实意义[1]。

变压器出现故障后，其油液溶解的气体与正常工作状态下的气体浓度具有明显差异，变压器油中溶解气体分析(dissolved gas analysis，DGA)基于此对变压器故障类别进行识别[2]，方法简单实用，但故障类型的判定过于依赖专家经验，存在故障类别判定不全，无法识别多故障类别的局限。

尹豪杰[3]在DGA的基础上，将4种常见的单一预测方法和马尔科夫理论、诱导有序加权平均算子结合起来，提出了一种新的DGA预测模型；刘佳佳[4]将DGA和指标加权法结合起来，建立了一种变压器故障在线监测方法；葛许良[5]在DGA的基础上，构建了分类深度置信网络(CDBN)诊断模型，提出了变压器在线监测与故障诊断方法；朱遥野[6]利用BP神经网络和灰色理论建立组合模型实现变压器故障性质诊断；贾京龙[7]分别选取深度学习机、极限学习机对变压器故障进行诊断；李春茂、徐牧等分别将粗糙集[8-9]、神经网络[10]、支持向量机[11-12]、专家系统[13]、模糊理论[14]等人工智能方法用于变压器的故障诊断，并取得较好的诊断效果。但是，这些方法在使用过程中，受到随机因素的影响，稳定性较差，并且随机初始化权值具有缺陷，容易陷入极限值，其可靠性和适应性有待提高。

本文对基于Bagging的集成算法做了进一步理论分析，提出基于SMOTE的Bagging改进算法，既克服了传统Bagging和Boosting算法存在盲目性和随机性的缺点，保证整体的分类准确率，又提高对少数类分类精度，并在基于DGA的变压器故障诊断中验证该方法的性能。

1 Bagging算法

1.1 Bagging算法的引入

与标准AdaBoost只适用于二分类任务不同，Bagging能不经修改地用于多分类、回归等任务。Bagging（bootstrap aggregating）算法通过构造预测函数系列，再以一定的方式重新组合成新的预测函数提高学习算法的准确度。逻辑上讲Bagging模型就是利用并行训练多个弱分类器，构成一个强分类器。单个弱学习算法通过多次使用该学习算法，得到新的预测函数序列，可以有效减少数据变化带来的误差，提升预测准确率。

1.2 Bagging算法过程

Bagging算法分为两个步骤：（1）分类，对每个基分类器抽样并训练得到强学习机，以强学习机作为模型，将多个弱分类器集成为强分类器；（2）自助采样，对基分类器的结果用加权或投票的方式进行合并，提高集成模型的预测精度，完成待诊断记录的故障判别[15]。

具体算法如下。

输入：训练集合T，测试数据x，分类方法C；

输出：x的类别判别R。

begin

for i=1，2，…，Ndo

Ti=bootstrap(T)；

Ci=C(Ti)；

Ri=Ci(x)；

endfor.

R=CntMax(Ri)；

end.

其中，CntMax表示寻求最多的支持类别，由N个分类器的判定结果得到。

自助采样也是Bagging的一个优点：因为每个基学习器只使用了初始训练集中约60%的样本，剩下的40%的样本可用作验证集对泛化性能进行“包外估计”，所以，记录每个基学习器的训练样本，并且令Tn表示tn实际使用的训练样本集，令Toob()

x表示对样本x的包外预测，即仅考虑那些未使用训练的基学习器在x上的预测，有：

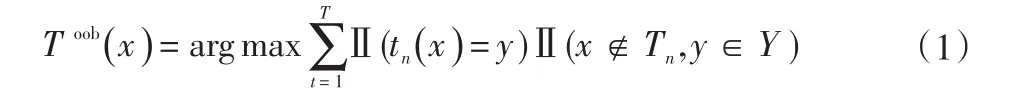
则Bagging泛化误差的包外估计为：

Bagging主要关注降低方差，因此它在支持向量机、神经网络等容易受样本扰动的学习器上效果更为明显。本文将支持向量机、神经网络等作为基学习器，将Bagging算法进行改进以提高变压器故障诊断的性能。

2 Bagging改进算法

传统的Bagging算法，对训练集样本随机采样，泛化能力强，分类精度高，但集成规模大，输出预测结果的速度较慢，并不是最理想的算法。

虚拟少数类向上采样是Chawla等[16]提出的一种向上采样方法，简称为SMOTE(synthetic minority over-sampling technique)，假设X是少数类样本的输入，它有a个同类最近邻，记为a1～an，随机选择ai，在X和ai之间进行随机线性插值，即可构造出新的少数类样本，新样本为

式中：u(0，1)为（0，1）之间的随机数。

SMOTE算法在原有训练集样本的基础上，按照一定的方法生成新样本，扩大样本个数，使分类器的分类平面从少数类向多数类扩展，从而不用担心分类器过度拟合的问题。

基于SMOTE的Bagging改进算法，首先利用SMOTE算法生成新样本，提高少数类样本与多数类样本之间的平衡性；接着通过对少数类样本加权的方式使基分类器偏重少数类样本，提高少数类的分类精度；最后利用Bagging算法进行集成改进，既提高了少数类分类精度，又保证了整体分类的准确率，具有很好效果。

定义：X为样本总集；n为样本数组；Xmin为X中的少数类样本；Xmax为X中的多数类数组样本；k为计数数组；w为样本权重；IB、OB为样本集合；R为任意样本；abs()为求绝对值，Mean()为求均值；Square()为求方差。

阐述算法步骤如下。

（1）确定少数类样本

分别记录样本总集X中每个类别所包含样本个数k和样本数组n；计算k的均值Mean(k)、方差Square(k)；若样本k[i]＜Mean(k)且 abs(k[i]-Mean(k))＞Square(k)，则此类为少数类样本：Xmin[j]=n[i]；反之为多数类样本：Xmax[j]=n[i]。

（2）增加少数类样本的数量

根据SMOTE算法，对少数类样本Xmin中的任意样本R求5个同类最近邻a1～a5，选择其中一个最近邻ai，计算R与ai的属性差值向量R-ai；选取(0，1)之间的随机数u，由式（1）得到新样本Rnew=R+u(0，1)·(R-ai)，以此类推，每个样本通过这种方式得到10个新样本，将所有新样本加入原样本总集，得到新的样本总集Xnew。

（3）确定训练样本权重

对新样本总集Xnew中的任意样本R，若R∈Xmax[]j，则样本的权重为：

式中：k[j]为Xmax[j]包含样本的个数；∑k[i]为所有样本的个数。

若R∈Xmin[]j，则样本的权重为：

式中：k[j]为Xmin[j]包含样本的个数；∑k[i]为所有样本的个数。

（4）对基分类器进行训练

IB为使用Bagging算法从新样本集Xnew抽取的样本，OB为未抽取的样本，用IB进行基分类器的训练，用OB对基分类器进行测试，测试结果作为每个基分类器的权重w，再以此为基础进行投票，即可确定分类结果。

为了验证Bagging改进算法的性能，选用接受者操作特性曲线（receiver operating characteristic curve，ROC曲线）下的面积（AUC）作为评价指标[17]。使用UCI中的不平衡类数据集Pima-Indians-Diabetes作为测试数据，Bagging算法的AUC=0.798，而Bagging改进算法的AUC=0.948，测试结果如图1所示。由图可知Bagging改进算法总体上表现出了良好的性能，X值从0.3开始，Y值几乎就达到了最佳并一直保持。由此可知，基于SMOTE的Bag-ging改进算法可以平衡少数类样本与多数类样本之间的差距，提高两者的平衡性，利用Bagging算法使用加权的形式进行集成，可以同时保证整体和少数类分类的分类精度。

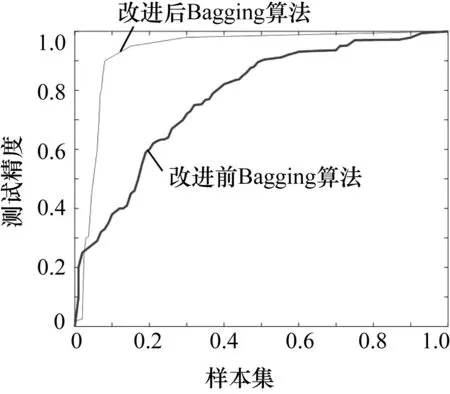
图1 Pima-Indians-Diabetes数据集ROC曲线

3 基于Bagging改进算法的变压器故障诊断

3.1 变压器故障类别的判定依据

变压器发生故障前往往会伴随一段放电或放热的过程，变压器油会溶解释放出氢气、甲烷、乙烷、乙烯、乙炔等5种特征气体，根据变压器正常状态和发生故障时5种特征气体的含量会发生改变的特点，通过对各气体成分含量的分析就可判断变压器故障。变压器的故障类别可以分为：（1）局部放电；（2）低能放电；（3）低能放电及过热；（4）电弧放电；（5）电弧放电及过热；（6）无故障；（7）低温过热；（8）中温过热；（9）高温过热。

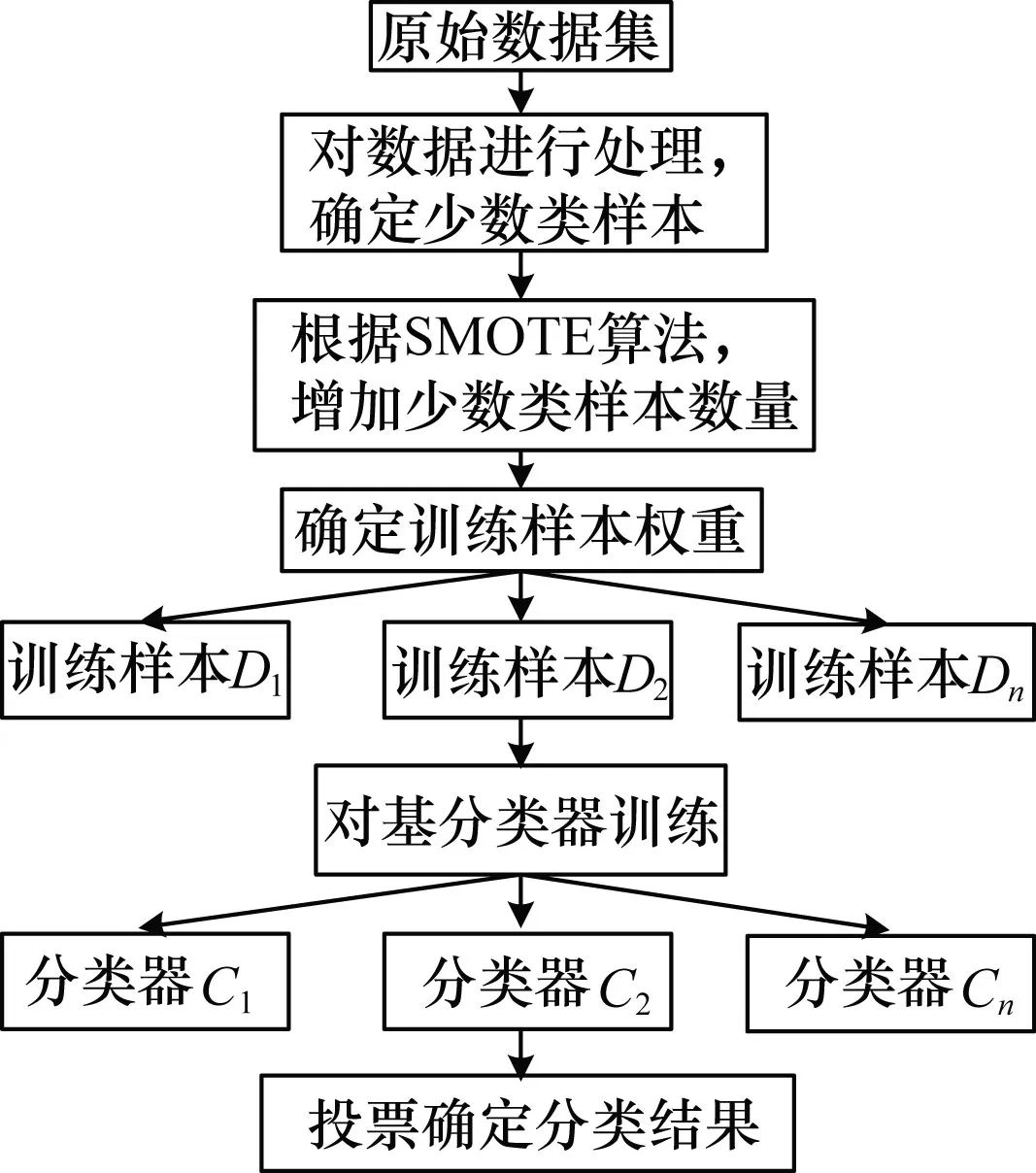
图2 Bagging改进算法的流程原理图

3.2 Bagging改进算法的流程

对变压器故障诊断来说，数据样本选取的合理性与故障预测正确率高低有密切联系，数据样本选取后，首先要对数据进行处理，以便建立可靠的训练模型。然后按照基于SMOTE的Bagging改进算法的步骤对数据样本进行训练、分类并最终确定结果。Bagging改进算法的流程原理图如图2所示。

利用Matlab将分类标签以及输入数据矩阵分开，把数据样本导入生成一张数据表格，对训练及预测数据样本集划分，将故障类别数据样本中的每一种故障样本数据划分成训练集和预测集两部分，再将两者分别重新组合在一起形成新的训练集和预测集，最后对数据采用X=normr(X)进行归一化预处理，使数据库中数据的行或列标准化。

3.3 仿真试验

本文以变压器油中气体含量的差异作为故障类别判断的依据，以文献[12]中的原始数据作为样本集，60%的数据用于训练集，40%用于测试集。180个故障样本，将其中的105个样本作为训练集，余下75个样本作为测试集。

运用Bagging改进算法对所选取的105个训练样本进行训练学习，其中弱分类器包含神经网络和k近邻、支持向量机、贝叶斯分类等。仿真模型运用Matlab集成学习工具箱中的fitcensemble 实现，其中：“goodResults={′TotalBoost′，′RUSBoost′，...，′LPBoost′，′AdaBoostM2，′Bag′;Mdl=fitcensemble(X，Y，′Method，′Bag，..′NumLearningCycles′，500，′Learners′，t)”。

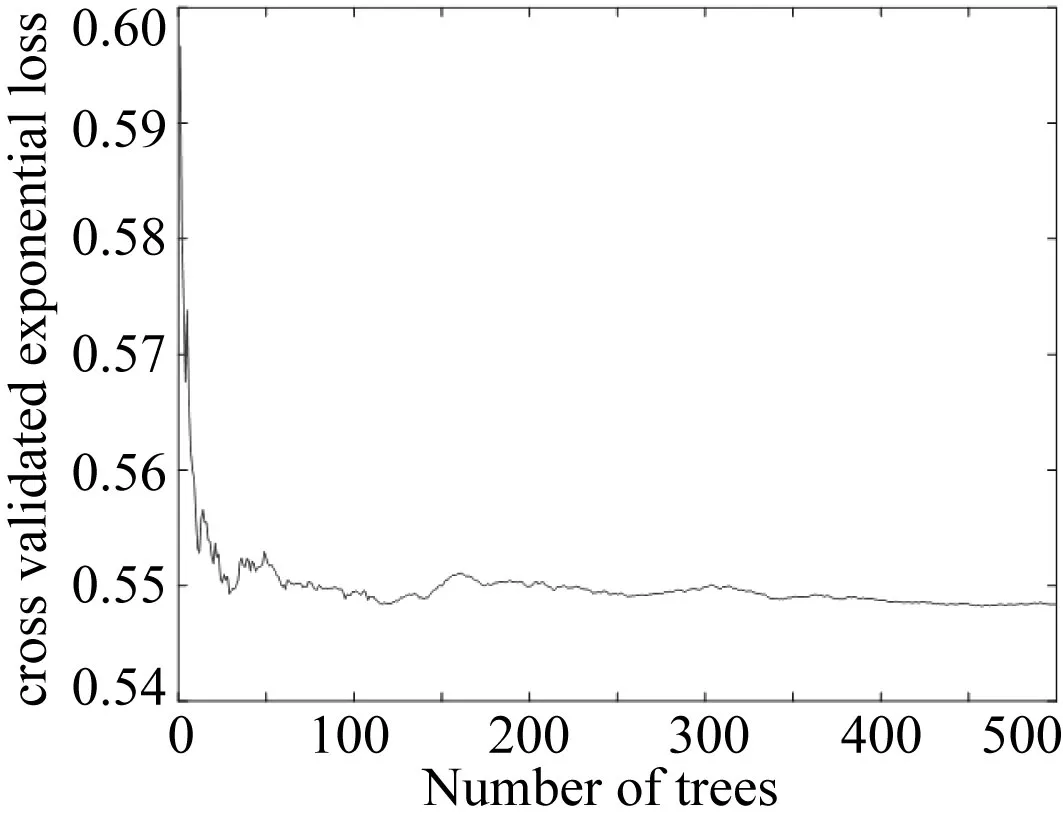
图3 迭代曲线

建立Bagging的预测模型时，首先对样本数据进行500次的交叉验证学习，使得到的结果能够达到最佳训练效果，预测精确趋近理想值，迭代曲线如图3所示。

对75组测试样本集，9种故障类别进行预测仿真试验，为了便于图形的可视化效果，对预测结果进行可视化处理，如图4所示。从图中可以看出，75组测试样本中，仅有7组样本的预测结果与实际结果不符，且集中在低温过热、中温过热和高温过热3种故障状态，其余故障状态则能够实现100%的准确预测。

图4 Bagging改进算法的变压器故障预测分类图

为了证明Bagging改进算法的性能，本文选取同一组样本集，同时用 TotalBoost，RUSBoost，LPBoost，AdaBoostM2 等Boosting衍生算法以及单分类器构成的SVMonly、BP神经网络和Bagging几种方法进行故障诊断预测精度比较试验，结果如表1所示。

表1 多种方法的故障诊断预测精度比较

从表中很容易看出，BP神经网络和单分类器SVMonly的预测精度最差，这也说明了变压器故障诊断难以建立精确的数学模型，使用单一分类器很难取得良好的预测效果，必须使用集成算法提高预测精度。从表中还可以看出，在同样的预测条件下，Bagging算法与Boosting算法性能基本接近，预测精度在84%～86.3%的区间范围内，说明了集成算法在变压器故障诊断中具有优越性，预测精度较高。

本文提出的Bagging改进算法通过增加少数类样本数量，减少少数类与多数类的不平衡性，调用弱学习算法完成对样本集的训练得到强学习机，利用强学习机作为变压器故障诊断模型，将多个弱分类器集成为强分类器，通过对模型的反复学习来提高集成模型的预测精度，提取数列具有的深层规律特征，以完成待诊断记录的故障判别。仿真实验得出Bagging改进算法的预测精度达到90.67%，超过其他几种方法，验证了此方法有较好的适应性和较高的诊断率，同时也证明了该算法的准确性和有效性。