根据巷道帮部围岩水平位移量选择合理的锚索支护参数

张周，吴德义

（安徽建筑大学，安徽 合肥 230022）

0 引言

随着煤矿开采逐渐由浅部转向深部， 煤矿中时常会出现严重的地质灾害问题[1]。 巷道开挖后改变了岩土体原来的应力状态， 若不及时进行相应的支护，很容易引起围岩的变形破坏，最终导致洞室出现严重毁坏[2]。 在煤矿开采过程中，锚杆（索）始终处于一个关键地位。 选择合理的支护参数对项目质量的提高和成本预算的减少具有重要意义。 在硬岩中布置锚杆的前提下布置锚索，分析不同的锚索预紧力、 锚索长度及不同的锚索间排距作用下的围岩水平方向位移量大小， 通过一系列对比并根据实际情况，来确定最合适的支护参数。

1 数值模型的建立

1.1 数值计算模型的建立

如图1 所示，以围岩直墙半圆拱形巷道的拱基线中心为原点建立数值模型，模拟的横向(X)、纵向（Y）和竖向（Z）依次为60 m、20 m 和60 m。 为了使模拟结果更准确，采用的划分网格比列为1:1。模型网格单元有2 万多个，在模型上面的边界处作用了16 MPa 的原岩应力。 在模型横向(X)、纵向（Y）和竖向（Z）处施加相应的约束条件。

图1 数值计算模型

利用平面应变情况来选取模型， 在巷道帮部和底部处的围岩上施加约束。 此外，本次模拟采用的是应变软化模型[3]。 巷道两边的变形是一样的情况，所以选取巷道左半部分进行水平方向位移量数值模拟。 如图2 所示，通过对OA 方向的切片数据处理来了解位移场的状况， 继而进一步分析巷道帮部围岩的稳定情况。 围岩巷道断面为直墙半圆拱形， 长为其峰值后强度伴随的应变衰减模型如表1，2 所示。5.2 m，高为5.2 m，半径为1.6 m。 围岩相关的物理力学参数和采用试验的方法所测得的各种岩性围岩及

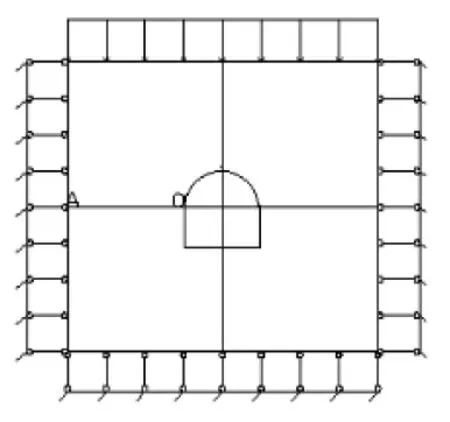
图2 数值计算模型示意

表1 围岩相关的物理力学参数

表2 不同岩性围岩的力学参数及峰后损伤强度、塑性系数衰减模型

1.2 应变软化本构模型

在煤巷现场提取试样，在实验室中制作成高为100 mm、半径为50 mm 的标准试件。 通过MTS 试验机的相关试验来确定本构模型中相关的塑性系数及损伤强度[4]，如表3 所示。

表3 实验测得本构模型中相关的塑性系数及损伤强度

通过现场试件所获得的本构模型中相关塑性系数及损伤强度能够较好地符合式（1）所表示的回归方程。式中：φ—残余内摩擦角 （°）；c—残余粘结强度（MPa）；k1、k2、k3、k4为系数。

通过式（1）和计算方法可以获得煤岩的应变软化本构相应的系数，如表4 所示。

表4 应变软化本构模型中的损伤强度及塑性系数

2 数值分析

在已经布置了2.5 m 长度、0.6 m×0.6 m 间排距和180 kN 的预紧力锚杆前提下， 选择合理的锚索参数来布置锚索， 通过FLAC3D 数值模拟软件对不同的锚索长度、 间排距和预紧力进行模拟，利用Tecplot 软件对巷道帮部围岩进行切片处理获取数据，并输入origin 软件中绘制出以距离巷道中心距离为横坐标、以围岩水平方向位移量为纵坐标的变化曲线图。

2.1 在硬岩中不同锚索长度的围岩水平位移量

在保证1.5 m×1.5 m 间排距和180 kN 预紧力一致的前提下，选择4 m、5 m、6.3 m 和7 m 的锚索进行模拟分析，通过图3 三个不同长度下的围岩水平位移变形情况来分析不同锚索长度与围岩位移变形量之间的关系。

图3 围岩在不同锚索长度支护下的水平位移量

通过对图3 围岩在不同长度锚索支护下出现的位移量进行分析， 发现随着锚索长度的增加，巷道围岩出现的位移变形量会减小。 当锚索长度由4 m 增加到5 m， 围岩水平方向的最大位移变形量从162 mm 降到142 mm；当锚索长度由5 m 增加到6.3 m， 围岩水平方向的最大位移变形量从142 mm降到130 mm；当锚索长度由6.3 m 增加到7 m 时，围岩水平方向最大位移量由130 mm 降低为124 mm。这些情况说明在一定范围里， 随着锚索长度增加，围岩位移变形量会逐渐变小， 最终位移量接近0，相对稳定。 在一定范围里，可加大锚索长度来控制围岩的变形， 但超出这个范围即使再增大长度，支护效果也没有显著改变，巷道围岩处在稳定状态。

在硬岩中不同锚索长度的围岩水平方向的位移量与距巷道中心距离之间的变化关系如图4 所示。

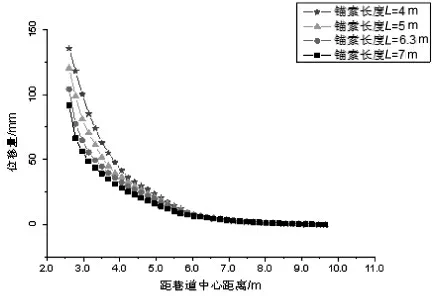
图4 在硬岩中不同锚索长度的围岩水平方向位移量与距巷道中心距离之间的变化曲线

由图4 可以看出，不同锚索长度的围岩水平方向位移量与距巷道中心距离之间的变化曲线整体表现为下降趋势，但当距巷道中心距离达到一定距离时，围岩水平位移量将不再发生改变，最终围岩位移量接近0，围岩表现相对稳定。 用4 m 和5 m长的锚索对巷道进行支护时，在距巷道中心2.6 m的位置分别产生了132 mm 和125 mm 的位移变形量，而用6.3 m 和7 m 的锚索支护时，产生的位移变形量都在100 mm 左右，变化不明显。 距巷道中心4.6 m 以内，用6.3 m 和7 m 的锚索支护时，围岩出现位移变化量比用5 m 的锚索小很多。 此外用6.3 m 和7 m 的锚索，曲线十分贴近，位移量改变不显著。 距巷道中心5.1 m 左右，三条曲线都十分贴近，表明采用三种长度锚索支护时，此处位移量基本一致。 距巷道中心7.1 m 左右时，位移量没有出现显著的改变，并逐渐接近0，围岩表现相对稳定。因此通过对比可以看出，选择6.3 m 的锚索较为合适。

2.2 在硬岩中不同锚索间排距的围岩水平位移量

在保证6.3 m 长度和180 kN 预紧力一致的前提下，选择1.1 m×1.1 m、1.3 m×1.3 m、1.5 m×1.5 m 和1.7 m×1.7 m 间排距的锚索进行模拟分析， 通过图5四个不同间排距下的围岩水平位移变形情况来分析不同锚索间排距与围岩位移变形量之间的关系。

通过对图5 围岩在不同间排距锚索支护下出现的位移量的分析，发现减小锚索之间的间距和排距，可以使巷道围岩位移变形量不断减小，直至接近0。当采用的间排距从1.7 m×1.7 m 减小到1.5 m×1.5 m 时， 巷道围岩位移变形量从151 mm 降低到133 mm；当采用的间排距从1.5 m×1.5 m 减小到1.3 m×1.3 m 时， 巷道围岩位移变形量从133 mm 降低到121 mm；当采用的间排距从1.5 m×1.5 m 减小到1.3 m×1.3 m 时， 巷道围岩位移变形量从121 mm 降低到115 mm。在一定范围内，随着锚索间排距的不断减小，围岩位移量减小，直到接近0。在一定范围内通过减小锚索间排距可以使位移量得到较好控制，但超出这个范围后，再减小间排距，位移量也不会有显著的改变，巷道围岩基本处在稳定状态。

图5 围岩在不同锚索间排距支护下的水平位移量

在硬岩中不同锚索间排距围岩水平方向的位移量与距巷道中心距离之间的变化关系如6 所示。

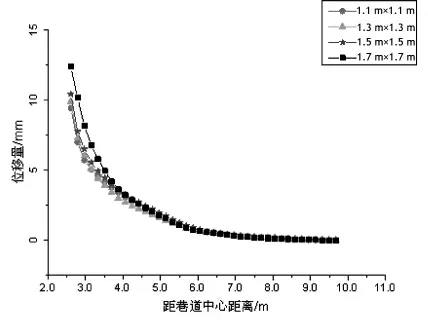
图6 不同锚索间排距的围岩水平方向位移量与距巷道中心距离之间的变化曲线

如图6 可知，随着距巷道中心的距离不断增加，围岩水平位移变形量逐渐减小， 直至围岩位移变形量接近0 时才趋于稳定。 采用1.1 m×1.1 m、1.3 m×1.3 m、1.5 m×1.5 m 和1.7 m×1.7 m 间排距的锚索在距巷道中心2.6 m 处出现的围岩水平位移变形量分别是95 mm、97 mm、100 mm 和119 mm， 显然采用1.1 m×1.1 m、1.3 m×1.3 m 和1.5 m×1.5 m 间排距的锚索围岩出现的位移量相差并不大。在距巷道中心4 m 内，采用1.7 m×1.7 m 间排距的锚索出现的位移量最大， 而采用1.1 m×1.1 m、1.3 m×1.3 m 和1.5 m×1.5 m 间排距的锚索时， 围岩水平方向位移量与距巷道中心距离之间的变化曲线非常贴近，接近重合，其支护效果差不多。 超出距巷道中心7 m时，图6 中的曲线基本汇合成一条曲线，位移量接近0，围岩基本稳定。 所以在满足性能要求、节省成本的前提下，通过对比分析可以看出，1.5 m×1.5 m间排距的锚索是相对合适的。

2.3 在硬岩中不同锚索预紧力的围岩水平位移量

在保证6.3 m 长度和1.5 m×1.5 m 间排距一致的前提下， 选择0 kN、60 kN、120 kN 和180 kN 预紧力的锚索进行模拟分析，通过图7 四个不同预紧力下的围岩水平位移变形情况来分析不同锚索预紧力与围岩位移变形量之间的关系。

图7 围岩在不同锚索预紧力支护下的水平位移量

由图7 可知，随着锚索预紧力的不断增加，巷道围岩水平位移变形量逐渐减小，直至接近0。 当采用的锚索预紧力从0 kN 变成60 kN 时，围岩水平方向最大位移变形量从170 mm 降低为151 mm；当采用的锚索预紧力从60 kN 变成120 kN 时，围岩水平方向最大位移变形量从151 mm 降低为138 mm；当采用的锚索预紧力从120 kN 变成180 kN 时，围岩水平方向最大位移变形量从138 mm 降低为133 mm。在一定范围内随着锚索预紧力的增加，围岩水平位移量会变小，最后位移量趋于0。 在一定范围内通过增加锚索预紧力可以减少围岩水平位移变形量，一旦超过这个范围，即使增大预紧力，支护效果也没有显著改善，此时围岩处于相对稳定状态。

图8 表示在不同预紧力作用下的围岩位移与巷道中心距离之间的变化关系， 随着距巷道中心距离的不断变大，位移量会出现变小，直到最后接近0，围岩表现相对稳定。 采用0 kN、60 kN、120 kN 和180 kN 的预紧力在距巷道中心为2.6 m 处产生的位移量分别为157 mm、138 mm、106 mm 和100 mm。在距巷道中心4.5 m 左右， 采用0 和60 kN 预紧力锚索出现的位移变形量最大。 从图中可以看出，采用120 kN 和180 kN 的预紧力锚索绘制出的曲线非常贴近，意味着采用这两种支护方式，在巷道帮部围岩出现的水平位移量差距不大，两者的支护效果差不多。 随着距巷道中心距离的不断增加，采用0 kN、60 kN、120 kN 和180 kN 预紧力锚索围岩水平方向位移量会减小，直到距巷道中心约为7.5 m时，位移量接近0，趋于稳定。经过分析，采用120 kN的预紧力较为合适。

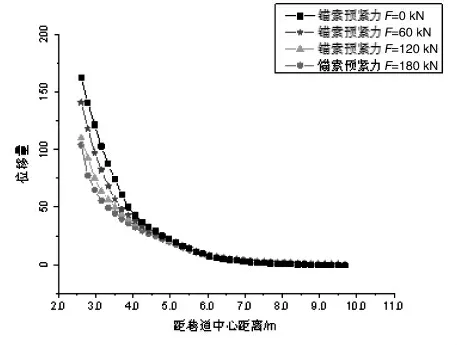
图8 不同锚索预紧力的围岩水平方向位移量与距巷道中心距离之间的变化曲线

综上所述， 通过对不同锚索支护参数的相关模拟， 确定在硬岩中的锚索支护采用长度6.3 m、1.5 m×1.5 m 间排距和120 kN 预紧力相对合理。

3 结语

在硬岩中，通过增大锚索预紧力（减小锚索间排距、增加锚索长度）会使围岩水平位移变形量发生减小，但减小到一定程度时，即使再增加锚索预紧力围岩水平位移量也不再发生显著变化，位移量趋近于0，围岩处于相对稳定状态。 通过对比分析，最终选取的锚索支护参数为6.3 m 的长度、1.5 m×1.5 m 的间排距和120 kN 的预紧力。