采空区移动变形的径向基函数神经网络概率积分法(RBF)反演

马学通，高德彬，杨映湖

(长安大学 地质工程与测绘学院，陕西 西安 710054)

0 引言

煤矿等采空区场地属不良建设场地，采空塌陷变形常造成地表建(构)筑物变形、耕地损毁、周边村庄的安全稳定性受影响等各种不良后果，严重威胁其变形影响范围内的人民生命财产安全[1-4]。工程实践中常采用概率积分法预测其影响范围，而其预测可靠性依赖计算参数选取。同时众多研究结果表明，概率积分法的参数选取与采矿地质条件密切相关[5-8]，且两者呈现出复杂的非线性关系。其参数反演常用最小二乘法[9]、智能算法[10]等。而径向基函数神经网络具有训练简洁、学习收敛速度快，以任意精度逼近任意函数的特点[11]。基于此，本文尝试选用径向基函数神经网络同时结合K层交叉验证法对概率积分法计算参数进行反演，为基于概率积分法预测采煤采空地表移动变形提供依据。

1 径向基函数神经网络

1.1 径向基函数(RBF)神经网络简介

径向基函数(Radial Basis Function)神经网络是Broomhead和Lowc于1988年根据生物神经元具有局部响应这一特点提出的，其结构图见图1。

图1 径向基函数神经网络结构

由图1可见，该神经网络包含三层结构，即只有一个隐藏层，输入层由N个感知单元构成，表示信源节点输入，且仅起到输入数据的作用。隐藏层含有M个径向基神经元(激活函数为RBF)，将低维非线性可分的输入映射到高维线性可分的空间，隐藏层节点的激活函数对输入局部响应，即当输入靠近基函数中央范围时，隐藏层节点将产生较大的输出，远离中心点时，输出将呈指数衰减。输出层含有P个线性神经元(激活函数为线性函数)，最终输出是隐藏层神经元输出的线性加权和。

径向基函数是中心点径向对称、取值仅依赖于中心距的非负实值函数，常采用高斯函数：

(1)

其最终输出为

(2)

式(2)中：wij为输出层第i个神经元与隐含层第j个神经元间的调节权重；M为隐藏层神经元数量；yj为神经网络的第j个最终输出值。

1.2 径向基函数(RBF)神经网络设计

长期采煤采空研究及工程实践，积累了大量矿区采空地表移动实测数据[10，13]。选取规范[9]提供部分矿区地表移动实测参数表的45个样本进行分析研究(表1)。每组样本由7个采矿地质条件(覆层岩性、煤层厚度、煤层倾角、采深、倾向采动程度、走向采动程度与松散层厚度)，以及概率积分法4个计算参数(下沉系数、水平移动系数、主要影响角正切与开采影响传播角)组成。借助45个样本的采矿地质条件与概率积分法参数关系，建立基于径向基函数神经网络模型对其进行预测分析。

1.3 K层交叉验证

为了从有限的数据中获取尽可能多的有效信息，同时避免数据过拟合的出现，因此选用K层交叉验证法进行训练验证。其训练验证步骤如下[12]：

1)将整个数据集随机分为K层；

2)用其中的K-1层进行模型训练，并采用第K层进行验证；

3)记录每一个预测结果的误差；

4)重复上述1)至3)过程，直至每“层”数据都作过验证集；

5)记录K个误差的平均值，即交叉验证误差，以用作衡量模型预测精度标准；

6)选取误差最小的模型作为最终输出模型。

将RBF模型与K层交叉验证相结合，可以有效避免人为划分数据集所产生的误差，显著提高模型的预测精度。

2 模型计算及误差分析

采用1.2节建立的RBF模型对表1中数据进行训练预测，其预测结果见图2至图5。

由图2至图5可见，采用径向基函数神经网络模型与K层交叉验证法相结合获得的预测值与实测值基本接近，可以为概率积分法提供较为准确的计算参数。

为了进一步验证该方法的预测精度，与文献[13]基于BP神经网络模型与支持向量机(SVM)的地表移动参数的预测结果进行比较分析。部分对比结果列于表2。

由表2可见，SVM模型均方根误差为BP模型的94.4%～123.15%，RBF模型均方根误差为BP模型的0.14%～60%，RBF模型均方根误差为SVM模型的0.57%～12.2%。由此可知，RBF模型的预测准确性更高，是一种有效的参数预测方法。

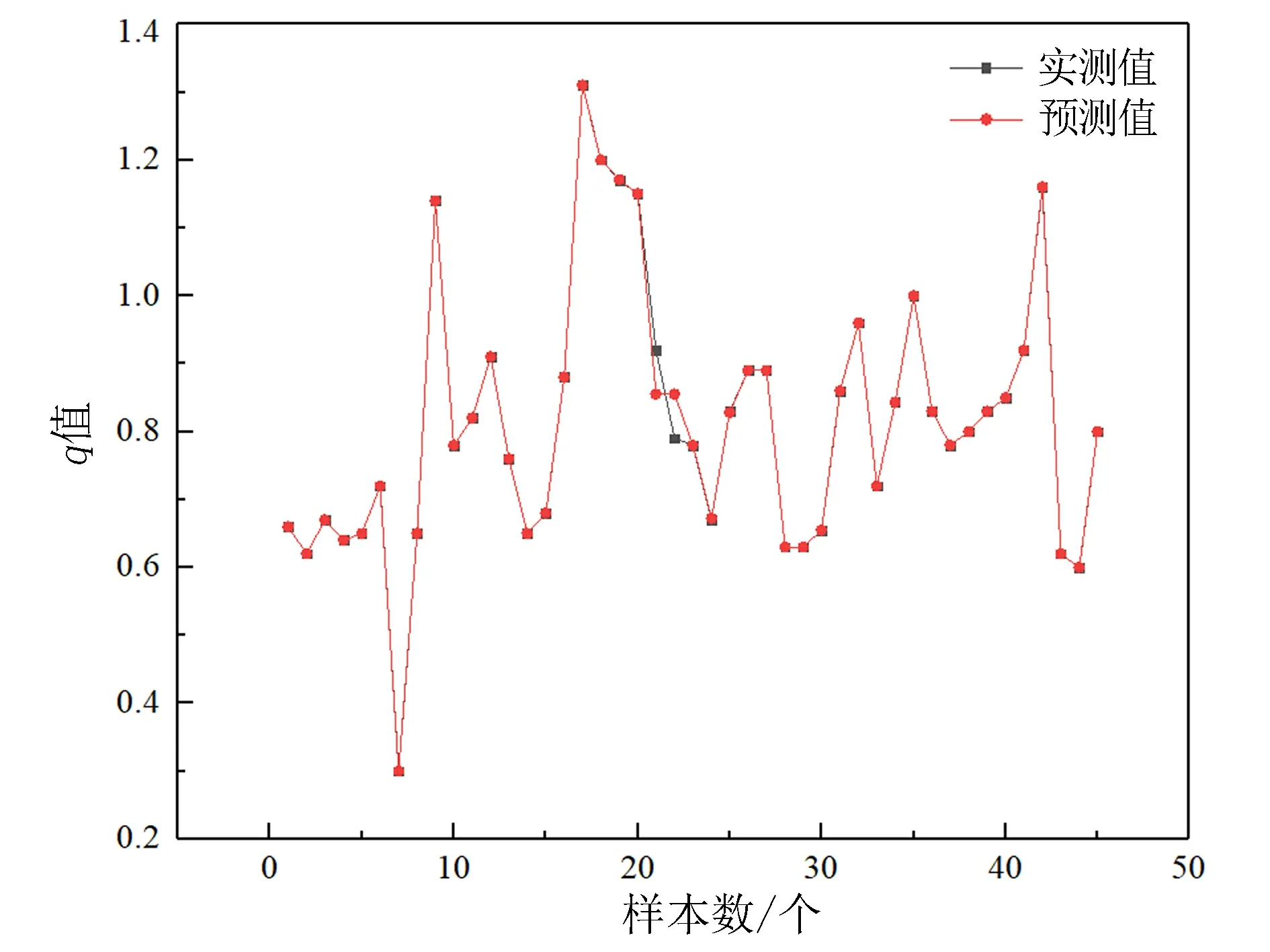
图2下沉系数q预测值与实测值对比 图3水平移动系数b预测值与实测值对比

Fig.2 Comparison of predicted and measured values of sinking coefficientqFig.3 Comparison of predicted and measured values of horizontal movement coefficientb

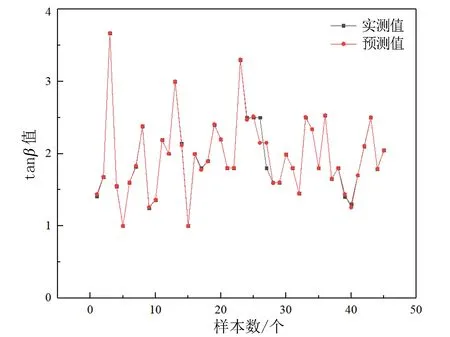
图4主要影响角正切tan预测值与实测值对比 图5开采影响传播角预测值与实测值对比

Fig.4 Comparison of predicted and measured values of the main influence angle tangent tanFig.5 Comparison of predicted and measured values of mining propagation angle

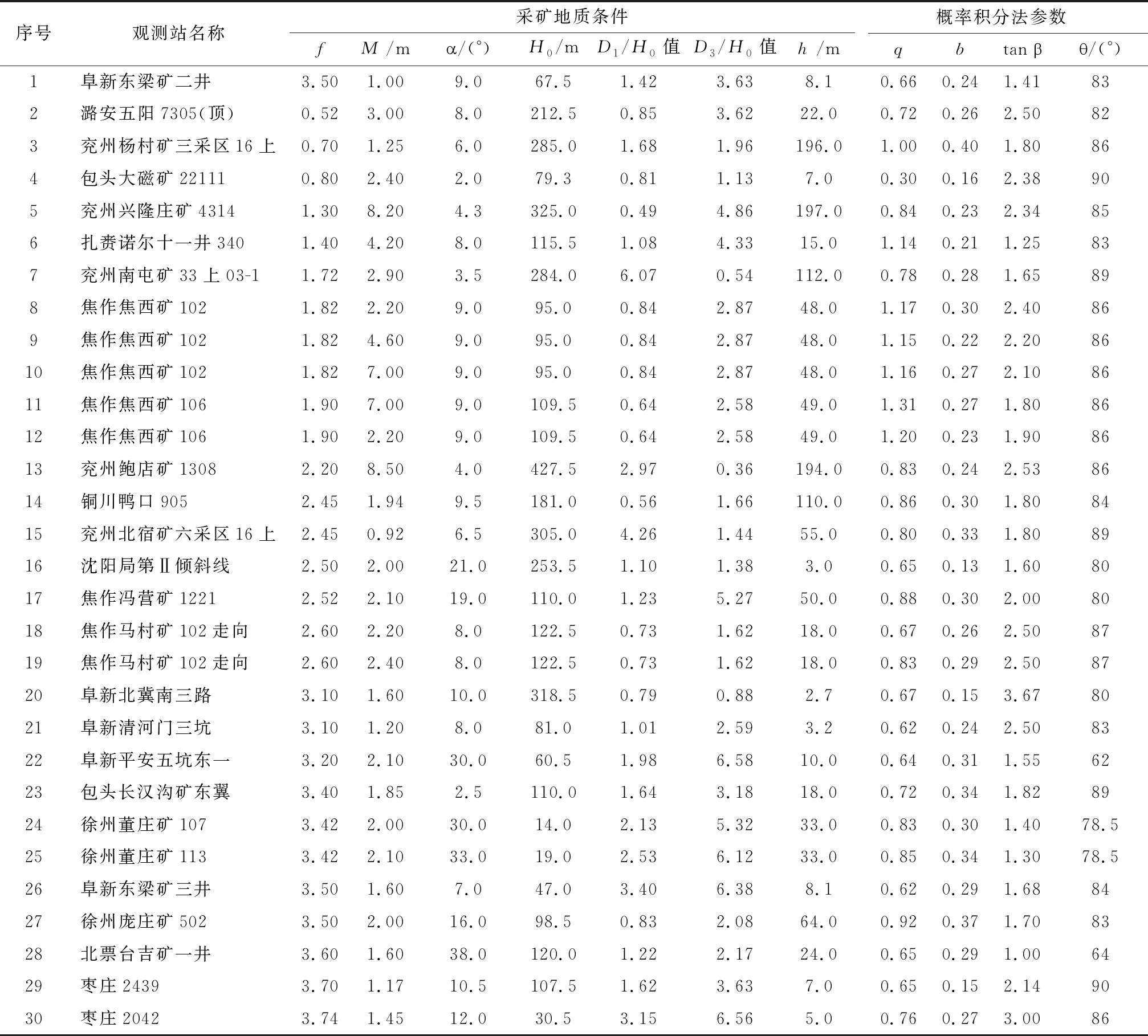
表1 典型矿区实测数据统计表(据文献[9，13] )

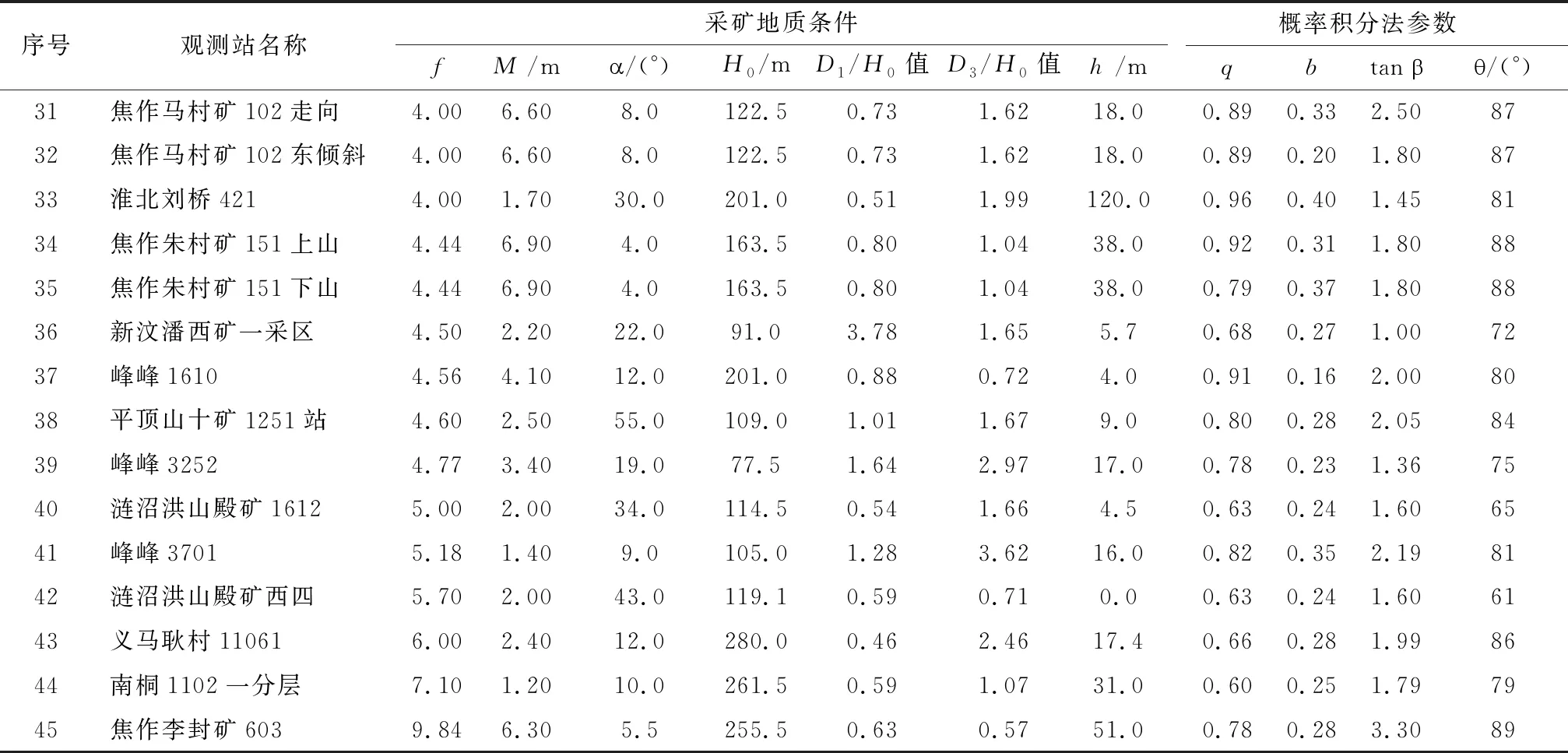
续表1

注：f为覆层岩性，M为煤层厚度，为煤层倾角，H0为采深，D1/H0值为倾向采动程度，D3/H0值为走向采动程度，h为松散层厚度；q为下沉系数，b为水平移动系数，tan为主要影响角正切，为开采影响传播角。

表2 各模型预测的均方根误差(RMSE)对比结果

3 结论

1)选取部分矿区地表移动实测参数，建立了概率积分法计算参数预测的径向基函数(RBF)神经网络预测模型，并结合K层交叉验证对已有数据进行随机分配训练及预测，避免了人为划分数据集的误差，有效提高了模型的预测精度。

2)与BP模型及SVM模型的预测结果进行对比发现，RBF模型的预测值具有更高精度，更加接近于实测值。因此在缺少采空变形监测的矿区，可根据规程的采矿地质条件参数并选用RBF模型预测计算参数，可满足采煤采空移动变形分析评价要求。