基于蒙特卡罗法的冲击力溯源系统不确定度评定

江文松, 王中宇, 罗 哉, 张 力, 胡晓峰

(1. 中国计量大学 计量测试工程学院, 浙江 杭州 310018;2. 北京航空航天大学 仪器科学与光电工程学院, 北京 100191;3. 北京长城计量测试技术研究所, 北京 100095)

1 引 言

冲击力溯源是通过一条具有规定不确定度的不间断的比较链,使测量的冲击力能够与规定参考值联系起来的特性。冲击力溯源技术被广泛地应用于航空发动机推力监测、航天器机翼载荷识别、汽车零部件性能检测、列车受电弓冲击试验、武器杀伤力评估等冲击载荷高精度测量及力传感器动态校准领域。作为力学量计量的核心,冲击力溯源是仪器设备性能可靠、工作稳定和数据准确的关键,并逐渐成为国际质量基础研究科学的热点问题之一[1～3]。冲击力溯源系统的测量不确定度来源于直接或间接测量过程,其中,直接测量过程是通过动态力值实现溯源的,间接测量过程是通过质量、加速度、位移和时间实现溯源的。通常利用测量不确定度表示指南(GUM)对这些测量量通过数值计算就能估计冲击力溯源系统的不确定度。但是,由于该溯源系统具有复杂的表征模型和未知的样本分布,GUM很难通过数值计算提高评定效率,也很难保证评定结果的准确可靠[4]。为此,Kumar G.提出了基于模糊逻辑推理的不确定度评定方法,解决参数未知、描述模糊和强非线性等知识模型的不确定性量化问题[5]。为了改善样本分布复杂和信息未知的影响,王中宇等将灰关联模型和自助熵理论引入复杂模型的不确定度评定上[6,7]。由于蒙特卡罗法(Monte Carlo method, MCM)不易受样本空间和模型非线性的影响,被用于复杂传递模型的不确定度评定[8～10]。尽管如此, MCM在模拟次数的确定和迭代停止条件的设计鲜有研究,影响不确定度的评定精度和效率。

本文利用蒙特卡罗方法对冲击力溯源系统进行测量不确定度的评定,主要包括冲击力溯源的表征、不确定性分量的表征和不确定度建模过程,通过设计冲击力溯源实验实现测量不确定度的MCM评定。

2 冲击力溯源的表征

溯源的冲击力是由落锤自由碰撞产生的,通常会以半正弦脉冲信号表现出来,如图1所示。

图1 冲击力的测量模型

冲击力的测量模型可以表征为[11]:

(1)

式中:F为溯源的冲击力;m1为落锤的质量;aequ(t)为落锤的等效加速度;a(xi,yi,t)为t时刻落锤上表面测点p(xi,yi)的加速度,采用激光外差干涉仪实时采集;n为落锤上表面测点p(xi,yi)的数量;ω0为冲击时初始角频率,与冲击信号的脉宽有关;E为落锤的杨氏模量,选铸钢材料时取198×109Pa;ρ为落锤的材料密度,取7.8×103kg/m3;h为落锤下落高度。

式(1)所示冲击力测量模型可简化为:

(2)

3 测量不确定度的MCM评定

3.1 不确定性分量的表征

由式(2)可知,冲击力溯源的不确定度既来源于力值发生装置,也来源于质量和加速度的测量过程。据此分析可知溯源系统的不确定度主要由落锤有效碰撞质量的测量误差、激光光轴与运动方向的不重合误差、激光外差干涉仪的测量误差、落锤的加速度分布不均匀、落锤的横向偏摆等引起。分别对这些误差项引起的不确定度进行建模。

3.1.1 有效碰撞质量误差

有效碰撞质量是由落锤产生,它可通过电子天平测量。选取的电子天平测量精度为±0.02 g(k=2)时,落锤质量示值误差Δm的标准差可表示为:

(3)

(4)

3.1.2 激光光轴与运动方向不重合

在理想的测量条件下,激光光轴与落锤的运动方向(即铅垂线方向)需要严格平行。受二维平台移动步距的限制,激光光轴与铅锤线方向之间会产生一个夹角γ,使激光光轴与运动方向不重合,如图2所示。

设激光外差干涉仪与落锤上表面测点之间的绝对测量距离为L,激光外差干涉仪测头与测点之间的垂直距离为Lcosγ。此时,落锤表面时变位移的测量误差为:

ΔL=L(1- cosγ)

(5)

在连续的时间历程上,冲击加速度是通过时变位移的二阶微分得到:

(6)

式中:L(t)为时变位移量;a(t)为冲击加速度。根据误差的传递关系,时变位移误差引起的加速度测量误差可以表示为:

Δaγ=1- cosγ

(7)

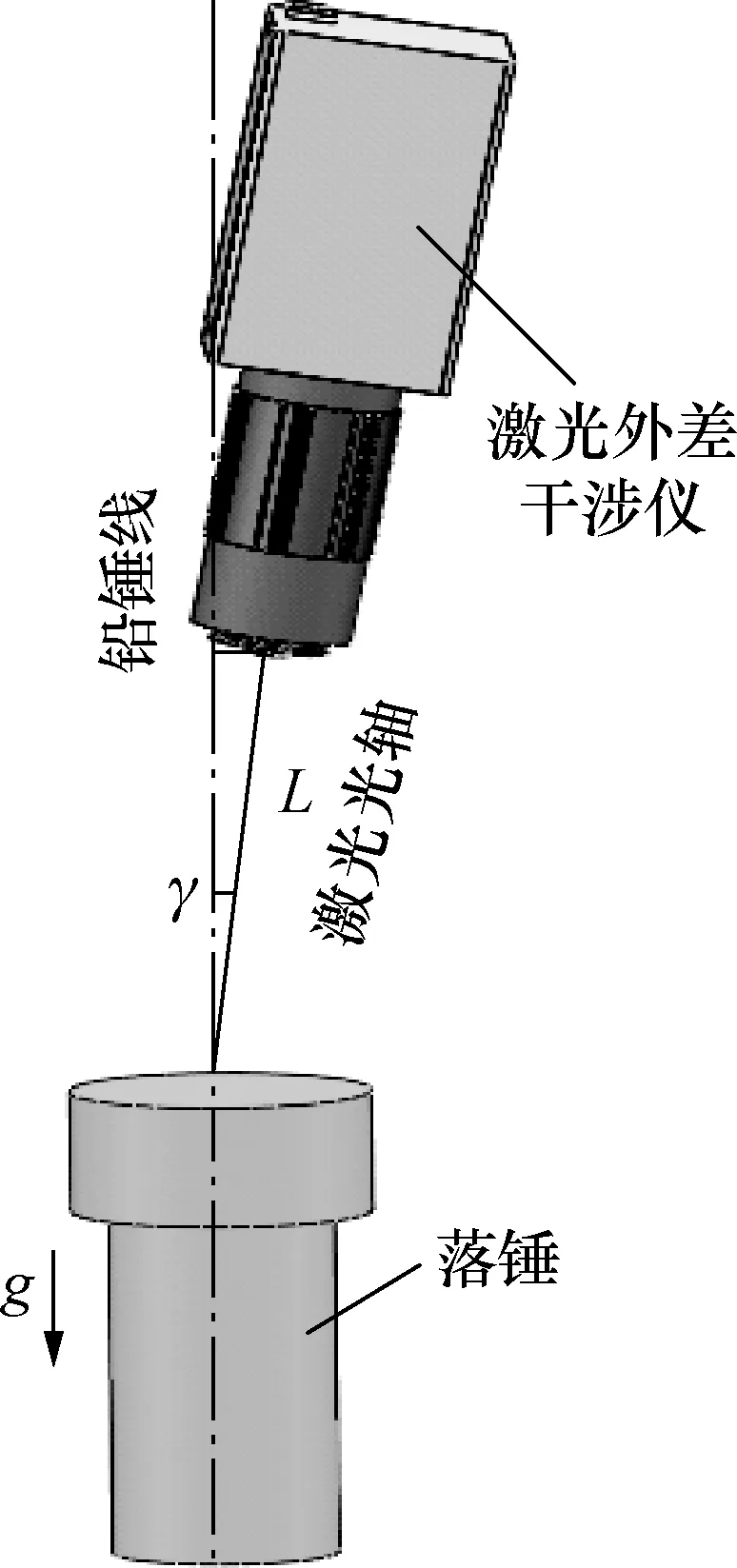
图2 激光光轴与铅垂线方向不重合模型

激光光轴与运动方向的夹角γ引起的测量误差服从投影分布,当二维平台对激光外差干涉仪的角度调整精度在[-0.002 9,0.002 9] rad区间时,加速度误差Δaγ的PDF服从投影分布,即:

(8)

此时的加速度误差Δaγ的期望和方差分别为:

(9)

3.1.3 激光外差干涉仪的测量误差

选用Polytec PSV-400型激光外差干涉仪,受到干涉仪灵敏度校准误差、线性度校准误差和采样时间误差等的综合影响,加速度的测量误差为0.2%(k=2),由加速度测量误差ΔaLDI引起的相对不确定度为:

(10)

因此,加速度测量不确定度满足均匀分布R[-0.1×10-2,0.1×10-2]。

3.1.4 落锤的加速度分布不均匀

在溯源时,通过测量落锤上表面5个均布测点的加速度并进行10次重复测量实验,就能求得落锤撞击时的加速度分布不均匀度。此时,落锤的加速度分布不均匀度χa(x,y,t)为:

(11)

式中:a(0,0)为同次测量时上表面中心点的加速度;n为上表面测点的数量。

3.1.5 落锤的横向偏摆

在冲击力溯源过程,落锤在非共振频率点的横向偏摆要求Txy-z≤5%,在共振频率点的横向偏摆要求Txy-z≤10%。相应地,落锤横向偏摆引起的加速度测量不确定度为:

(12)

一般地,溯源过程只考虑落锤在非共振频率点的横向偏摆,此时的加速度测量不确定度服从均匀分布R[-0.125×10-2,0.125×10-2]。

3.1.6 落锤的尺寸测量误差

利用示值最大测量误差为±0.07 mm(k=2)的游标卡尺测量落锤的下落高度h时,示值误差Δh的标准差为0.7×10-4h/2。尺寸测量的误差满足正态分布N(0,(0.35×10-4·h)2)。

3.1.7 电压测量误差

在加速度测量时,激光外差干涉仪输出的是表示位移的电压信号,当采用12位数据采集卡测量时,电压输出波形的测量及其二次微分的误差Δu为0.1%(k=2),由此引起不确定度为:

(13)

因此,电压测量不确定度满足均匀分布R[-0.05×10-2,0.05×10-2]。

3.2 不确定度评定模型

冲击力溯源系统的表征模型中7个输入量可以表示为向量x=(x1,x2,x3,x4,x5,x6,x7)=(Δm, Δaγ, ΔaLDI,χa,δxy-z, Δh, Δu)的形式。在置信概率p确定的情况下,抽样次数Mmc满足如式(14)所示关系[12～15]。

(14)

实际上,抽样次数Mmc的选择对冲击力溯源的不确定度评定至关重要:样本容量越大,迭代结果越稳定,越能反映输入量的总体分布。为了使溯源表征模型输入量的样本分布最佳逼近其总体分布,将M0作为初始抽样次数,利用相邻迭代次数之间的相对误差作为适应度函数,即

(15)

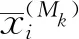
然后,利用基于梅森旋转算法(Mersenne twister)的伪随机数生成技术,分别对具有不同样本PDF的分量进行Mmc次抽样。抽样后的输入量可以表示为如下的矩阵形式:

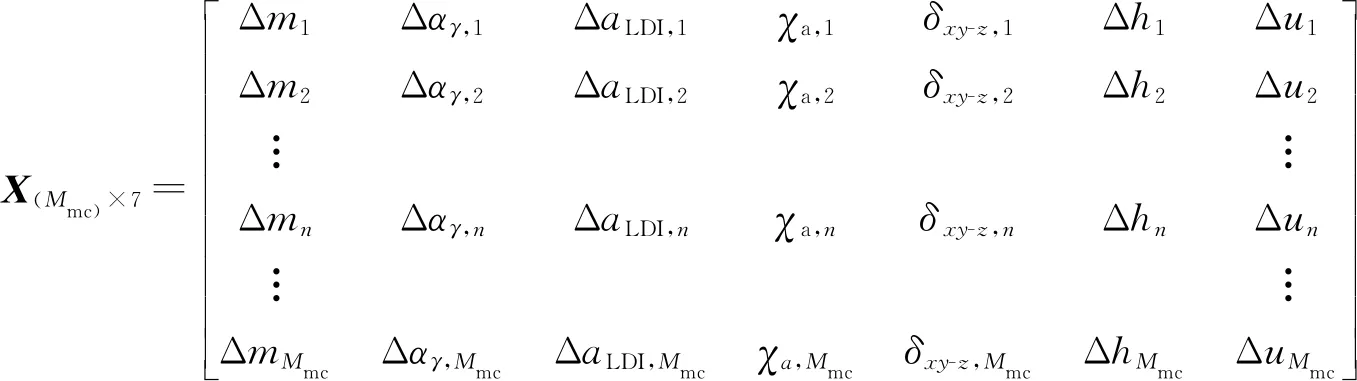
(16)

式中:X(Mmc)×7为一个(Mmc)×7的矩阵,其每一列中的所有元素是该列输入量经过Mmc次模拟后抽取的样本。当抽样次数为r时,模拟输出的冲击力F(xr)为:

F(xr)=F(x1,r,x2,r,x3,r,x4,r,x5,r,x6,r,x7,r)

(17)

式中r=1,2,…,Mmc。根据式(17)就能模拟出冲击力溯源系统的测量不确定度。

4 实验与不确定度评定

4.1 冲击力溯源装置的工作原理

利用一套冲击力溯源系统验证上述模型的有效性。它主要由砧体底座、导轨、锤架、隔振基座、弹簧减震器、力传感器、落锤、激光外差干涉测振仪、二维移动平台和测量支架组成,如图3所示。

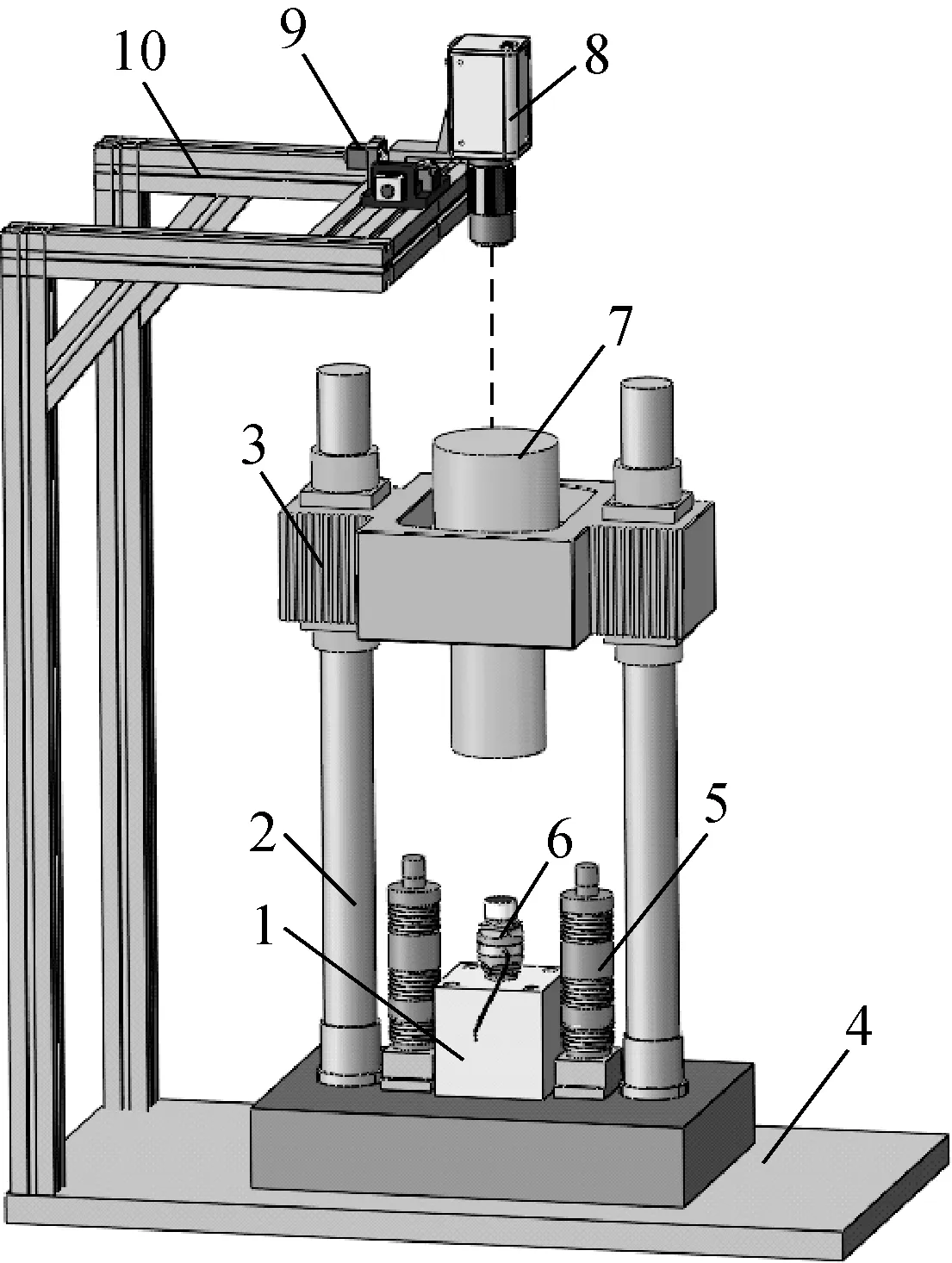
图3 冲击力溯源系统原理图

力传感器安装在砧体底座上,正面接受落锤施加的冲击力。落锤在自由落体过程的运动参量通过激光外差干涉测量系统采集。激光外差干涉测量系统主要由测量支架、二维移动平台和激光外差干涉测振仪等设备组成。

冲击力溯源主要包括3步:首先,悬挂在锤架上的落锤沿着导轨提升至预设高度。然后,锤架从导轨上释放并跟随落锤一起沿铅垂线方向自由下落,锤架砸落到弹簧减震器之后便悬停并与落锤分离。最后,落锤继续下落并撞击到砧体底座上的力传感器产生冲击力。

为了降低落锤横向偏摆引起的加速度分布不均,在落锤上表面选取均匀分布的5个点作为加速度的测点。其中,中心点P0位于落锤的表面圆心,其它4个测点与中心点的直线距离均为20.0 mm,如图4所示。利用激光外差干涉测量系统同时采集上述5个均匀分布测点的加速度并计算各点的加速度峰值,如表1所示。

图4 落锤上表面加速度的测量点分布

根据表1的计算结果可以看出,落锤上表面加速度幅值不均匀度的均值为0.789%,标准差为0.065%,可见落锤的加速度分布不均匀度的震荡区间有限。由式(11),加速度幅值不均匀度引起的不确定度服从均匀分布R[-0.789×10-2,0.789×10-2]。

4.2 溯源冲击力的测量不确定度评定

根据MCM评定方法,将冲击力测量模型中各不确定变量作为模型的输入,建立输入量的分布及特征值表征关系。利用上述测量结果计算输入量的概率分布及其特征值,如表2所示。

选取置信概率p=95%,此时抽样次数应满足

Mmc>M0=2×105

将M0作为初始迭代次数,迭代预设精度取0.001 N,根据式(15)中的适应度函数进行迭代抽样,统计出样本量稳定时的抽样结果,如图5所示。

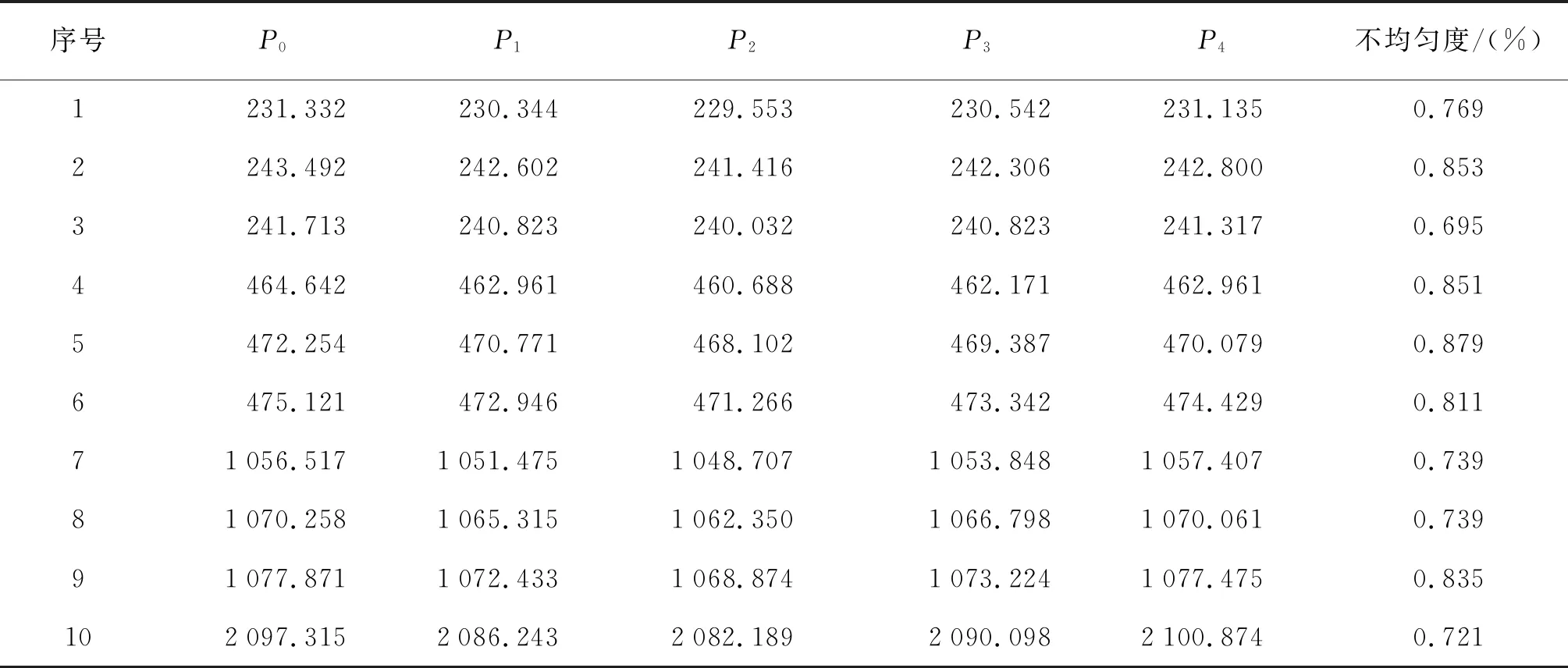
表1 落锤上表面的加速度峰值

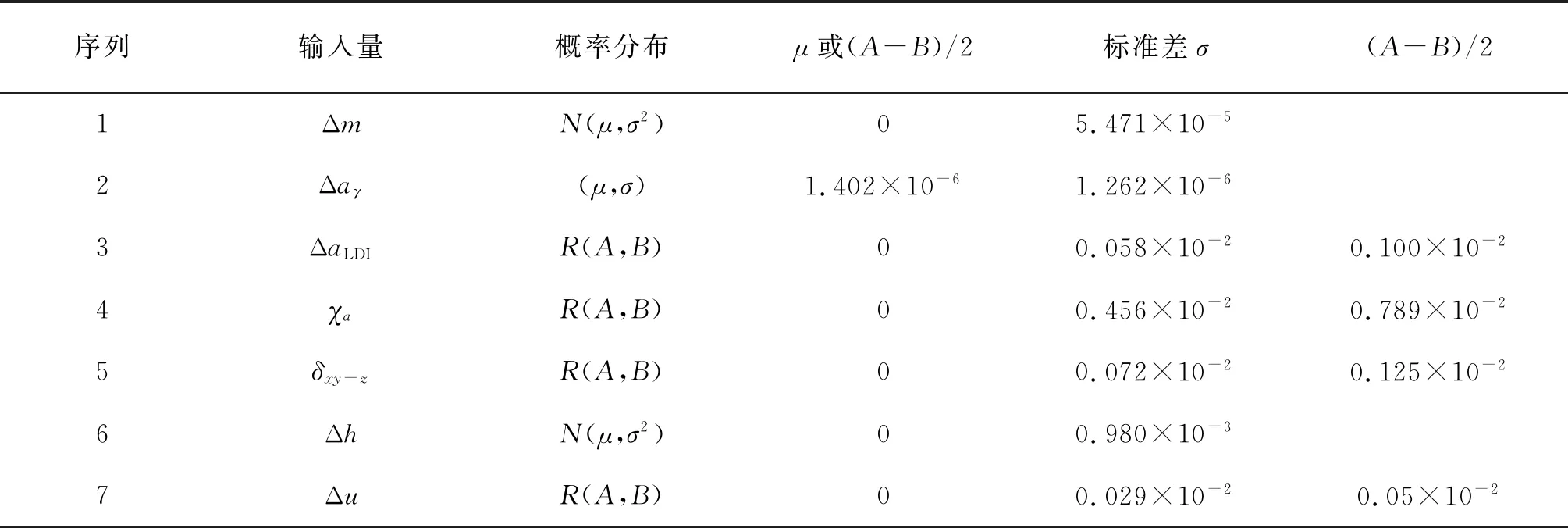
表2 冲击力溯源表征模型的输入量分布及特征值

注:μ为期望值;σ为标准差;A为样本区间上界;B为样本区间下界。

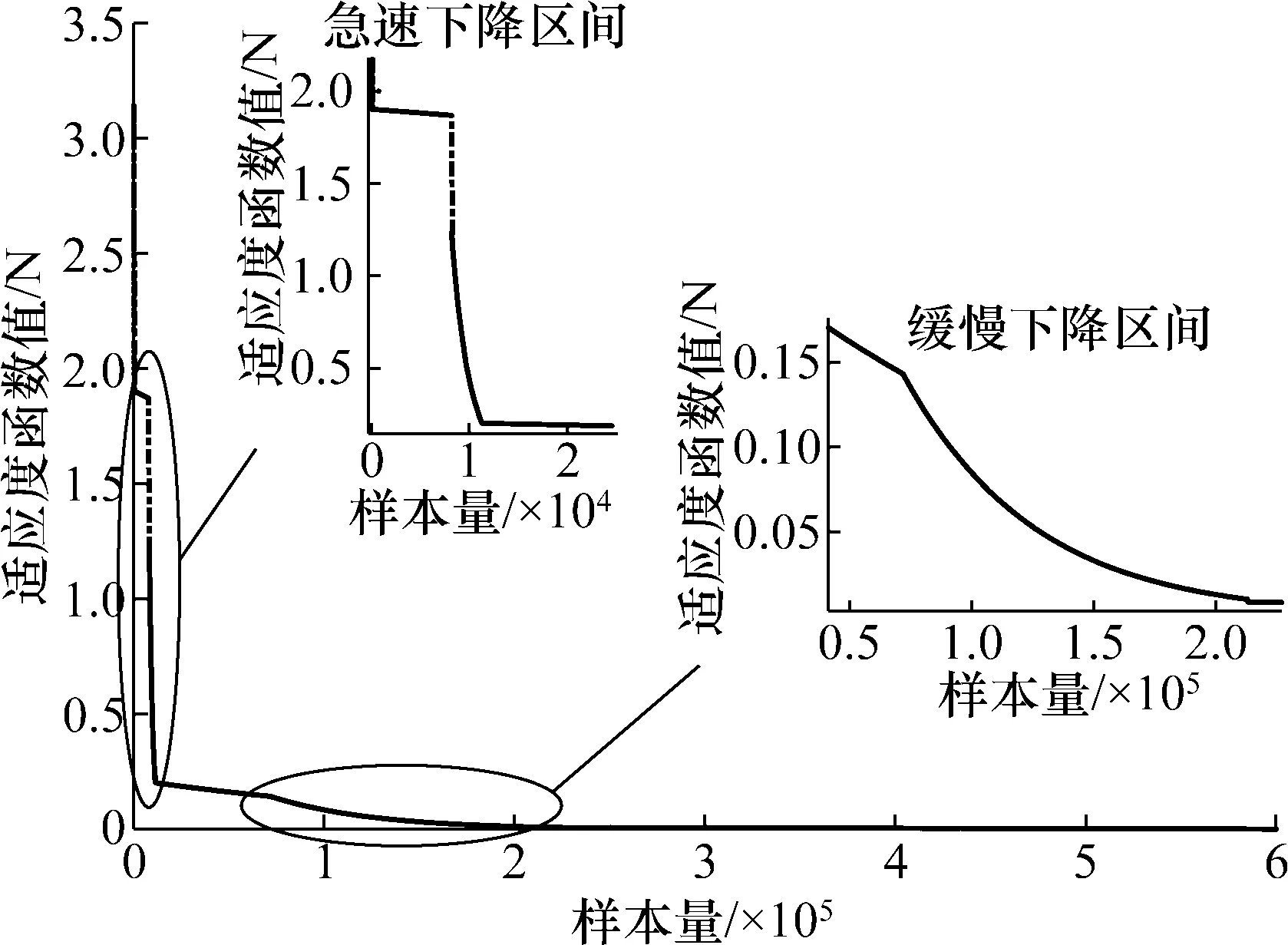
图5 样本空间的抽样迭代过程

由图5可以看出适应度函数经过1193次抽样后快速下降趋稳;当样本量达到2.13×105次时,适应度函数已经满足预设精度要求,为了使样本统计结果更为稳定,本文选取抽样次数为4×105次。

模型经过Mmc次抽样,就能统计出各相互独立的输入量对应PDF的样本直方图,如图6所示。

将式(16)中每次抽取的样本代入式(2)的冲击力测量模型,就能模拟出该次抽样的输出冲击力。将各输入量的概率密度函数代入式(17),求出输出量F的估计值分布及其样本统计直方图,如图7所示,可见,输出量的样本近似对称分布。

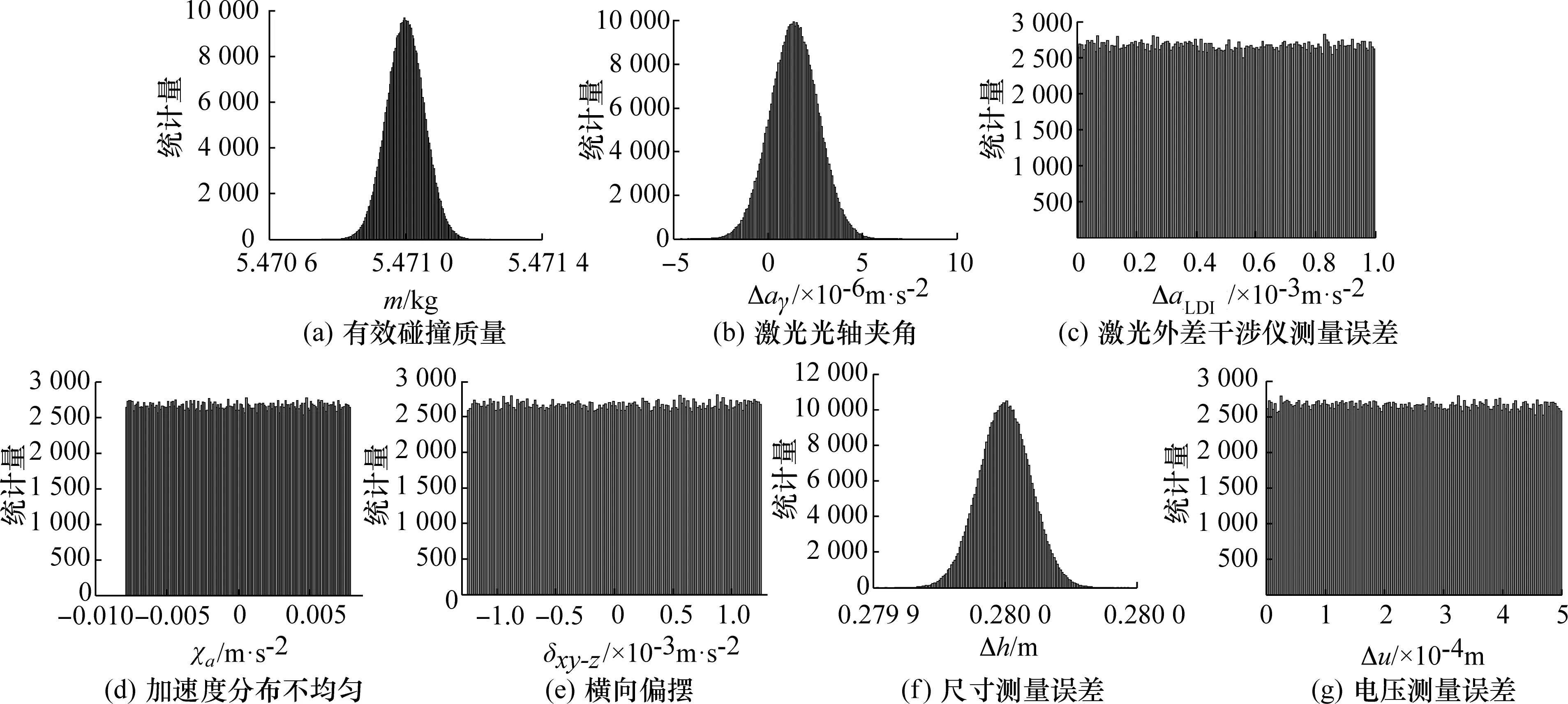
图6 冲击力溯源表征模型的输入量样本直方图

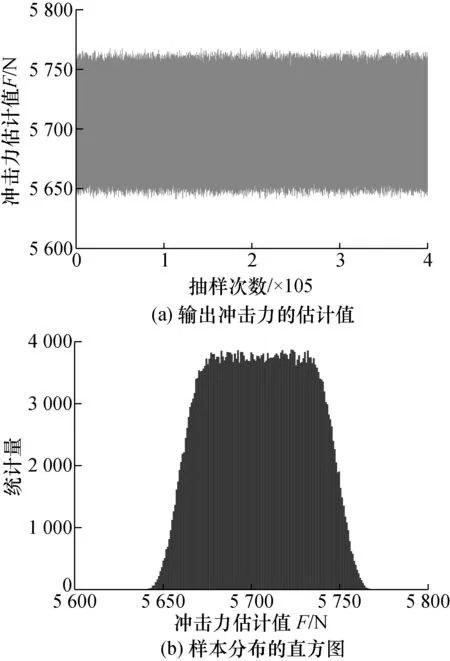
图7 输出冲击力的估计值及样本直方图

(18)

由输出估计样本的近似对称分布,可求的扩展不确定度Up为:

(19)

式中:F′为F(xr)经过升序重排后的新序列;p为置信概率。利用式(19)可求得p=95%时的扩展不确定度U0.95=46.685 N。

相对扩展不确定度Urel为:

(20)

在对冲击力溯源系统进行测量不确定度评定时,当撞击面处的Kistler9331B力传感器输出峰值为5 689.894 N的冲击力时,对应测量不确定度的评定结果如表3所示。

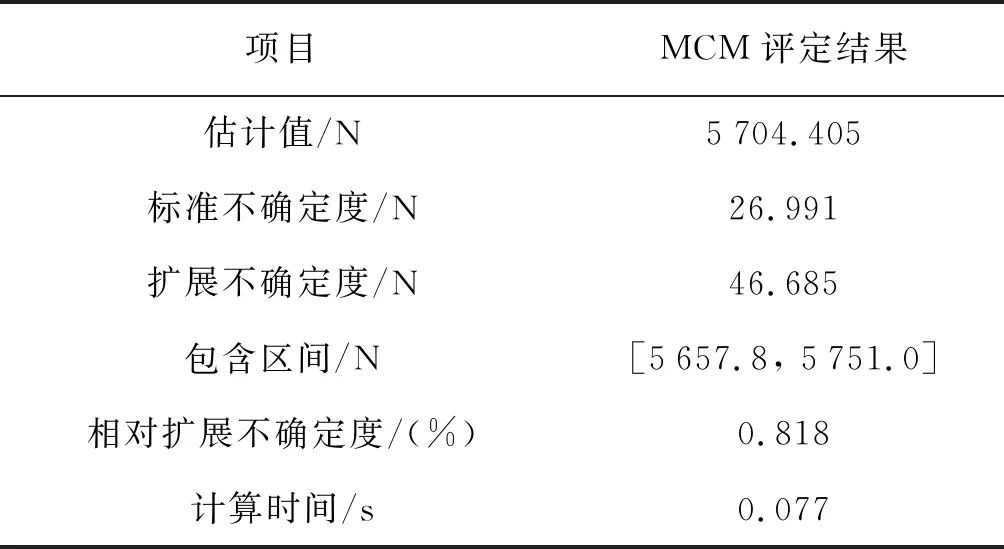
表3 冲击力溯源系统的测量不确定度MCM评定结果

根据输入量的样本分布和MCM评定结果可知,冲击力溯源系统的不确定度主要是由落锤上表面加速度分布不均匀和横向偏摆引起。在进行冲击力溯源时,通过改善落锤上表面加速度分布的均匀性和降低落锤冲击过程的横向偏摆,均能较好地提高溯源精度。MCM法通过适应度函数直接判定最优抽样次数,计算时间为0.077 s。

5 结 论

冲击力溯源系统的不确定度评定是动态力计量体系的关键技术,本文主要研究结论如下:1)利用MCM方法对动态力溯源系统进行不确定度评定,在95%的置信水平下,冲击力溯源系统的相对扩展不确定度优于0.818%。评定结果表明,冲击力溯源系统的不确定度主要来源于落锤上表面加速度分布不均匀和横向偏摆。2)本文建立的MCM方法是对冲击力溯源系统测量不确定度评定的有效尝试和补充。