基于数据驱动的电动出租车充电站规划方法研究
2020-05-28邓昌棉张勇
邓昌棉 张勇
摘 要:为了规划城市道路网上电动出租车的充电基础设施,以满足整个城市电动出租车的充电需求,本文利用出租车乘客起讫点大数据,基于M/M/K排队模型提出电动出租车在充电站处排队模型,建立行驶距离最小的充电站选址优化模型及遗传求解算法。以苏州市出租车GPS数据为例,对模型进行验证。研究结果表明:随着充电速率的增加,将减少电动出租车充电需求的单位成本,从而增加充电站设站数量,由此将缩短电动出租车充电的行驶总距离;基于不同工作日GPS大数据求解的充电站选址在道路网中呈簇状分布,模型结果具有稳健性,这表明可以在邻近区域内寻找可布设点建设充电站。研究结果可为出租车充电站规划和运营提供决策依据。
关键词:电动出租车;充电站选址规划;GPS大数据;M/M/K排队模型
Abstract:In order to plan the charging infrastructure of electric taxis on urban roads to meet the charge needs of electric taxis in the entire city, utilizing the big data of taxi passengers, a queueing model of electric taxis charging at charging station based on the M/M/K queuing model and a location optimal model of electric taxi charging stations for minimum total travel distance and models algorithm are all proposed. The GPS data of Suzhou taxi is used to verify the model. The research results show that with the increase of the charging rate, the unit cost of the electric taxi charging demand will be reduced, while the number of charging stations increases, thus reducing the total distance of electric taxis. The locations of charging stations are distributed in clusters in the road network, thus the model results are robust. This means that applicable sites can be found to build charging stations in adjacent areas. The research results can provide decision basis for the planning and operation of taxi charging stations.
Keywords:Electric taxi; battery charging station location planning; GPS big data; M/M/K queueing model
0 引言
電动汽车因其环保、经济而发展非常迅速[1],太原、深圳、广州和北京等城市的电动出租车的市场占有率接近100%。目前电动出租车主要为插电式充电(以下简称插电),其耗时较长。例如:北汽慢充8 h、快充2 h;特斯拉慢充10 h、快充1.5 h;比亚迪慢充20 h、快充2 h。由于电动出租车需要全天候运营,其续航里程较短,充电耗时长,制约了电动出租车的普及。因此,如何规划电动出租车充电基础设施以满足其需求,是满足电动出租车交通运输的首要问题。
目前,许多学者对插电式电动出租车的充电基础设施规划方法开展研究。此类选址研究大致有3类:P-中值问题[2]、P-中心问题[3]和覆盖问题[4]。第一类P-中值问题是指给定设施数P,确定设施的位置使得需求点到其分配设施的距离与相应的需求量乘积之和最小,如Shahraki等[5]和Ghamami等[6]进行了此类研究。第二类P-中心问题是指在网络中给定P个设施,使得全部需求点到与其最近设施的距离之中最大值最小化的问题,如Li等[7]和Wong等[8]进行了此类研究。第三类覆盖问题可分为两大类[9],集覆盖选址问题和最大覆盖选址问题,前者即在满足全部需求被覆盖的情况下,设施数目最少或设施建设成本最低的问题,如Tu等[10]和Hu等[11]进行了此类研究;后者在已知服务站数目和服务半径的情况下,确定P个服务站的最优位置使得其覆盖的需求量最大的问题,如Jung等[12]和Asamer等[13]进行了此类研究。
由于乘客搭乘出租车的OD(出租车起终点间的交通出行量)对随机性大,对电动出租车充电站的选址有较大影响。而出租车GPS采集的数据为分析出租车的运营特性提供了可能,由此也为更好地规划充电基础设施提供了新的思路[14]。基于出租车GPS采集的数据可预估充电需求,因此规划充电站至关重要。Lu等[15]基于时空网络开发模型优化出租车队的最佳时间表,实现车队总运营成本的最小化。Kang等[16]从电动出租车寿命的角度,研究了淘汰燃油出租车的经济可行性,但并未对出租车充电过程进行研究。上述研究存在两个缺陷:一方面没有考虑电动出租车到站时无空闲充电桩的概率,这对出租车充电的影响较大;另一方面,以往研究只能粗略估计出租车出行需求,容易造成规划的充电站规模出现不足或过剩。这两方面决定着以往的研究难以满足电动出租车对电能补充的苛刻要求。因此必须深入考察电动出租车在充电站处有空闲充电桩的概率,同时利用大数据精确掌握路网上的OD需求,由此实现电动出租车充电设施的科学规划。
本文根据出租车运营大数据获得高时空精度的出租车充电OD对需求,提出插电式出租车充电设施规划的科学方法。
(1)为描述插电式出租车充电过程,基于M/M/K排队模型,建立出租车在站充电的随机过程的数学描述。
(2)以出租车充电OD对需求最小行驶总距离为目标,考虑总成本和有空闲充电桩概率等约束,建立充电站选址和充电桩数量的一体化决策模型及求解算法。
(3)对不同工作日充电站选址分析,揭示基于出租车大数据的充电站选址的稳健性。
1 模型构建
1.1 基本假设
本文仅考虑研究范围内的主要路网(包括快速路和主干道),其路网G由路段和节点组成,记为G=V,N。其中,V为节点集合,N为路段集合。研究范围内的划分小区记为A。为方便建模,进行以下基本假设:
A1:出租车到达充电站时,以先到先服务的顺序进行充电。
A2:有充电需求的电动出租车到达充电站的间隔时间服从泊松分布,充电时间服从负指数分布。
A3:在划分小区A的出租车充电OD对需求将选择距离该小区最近的路网节点进入路网。
A4:假设一辆出租车某一订单结束到下一订单开始的间隔时间大于1 h认为出租车去充电站进行充电。
A5:出租车司机会在电量耗尽前到达充电站进行充电。
A6:假定出租车司机在到达充电站前是无法准确预知是否有空闲充电桩。
1.2 出租车充电随机性分析
一辆电动出租车到达后,如果充电站此时有空闲充电桩,那么将会进行充电并充满电后离开;如果没有空闲充电桩,将会在充电站处排队等待。由上述充电过程可知,充电桩数量会影响电动出租车在充电站補充能源的等待时间。根据上述A1假设,出租车随机到达充电站,以先到先服务原则进行充电。将k个充电桩和电动出租车数量构成的系统视为M/M/K排队系统。
利用M/M/K排队理论计算充电站没有空闲充电桩的概率[17]。令Pn表示系统中出租车数为n的概率(n=0,1,2,3,…,∞),μ为出租车充电的速率,λ为出租车到达充电站的速率,ρ=λ/(k·μ)<1,根据M/M/K排队理论计算系统中不同出租数量的状态概率为:
1.3 充电站选址分析
1.3.1 充电需求分析
由于出租车通常安装GPS设备用于导航和运行监控。利用出租车运营轨迹数据可实现出租车出行需求的准确估计,如:Wang等[18]和Chrysostomou等[19]的研究。根据出租车GPS数据来讨论出租车的充电需求。首先根据假设A4,一辆出租车某一订单结束为O和下一订单开始为D转换成充电OD对需求;其次将研究区域主要道路网划分成1 km×1 km小区,然后根据出租车充电OD对需求,将各个出租车需求匹配到对应的小区,因此可以得到各个小区间的OD对矩阵;最后根据假设A3,通过路网对各个小区间的OD对矩阵进行转移和分配,得到路网节点OD对矩阵。
由于已知出租车路网OD对矩阵,其他车辆路网流量未知,因此忽略出租车发生拥堵的情况。根据全有全无分配方法来分配电动出租车的充电需求。充电站j的充电需求估计为:
1.3.2 充电站优化模型
在电动出租车电量耗尽之前,电动出租车司机总是会选择最短的路径去进行充电。对此,提出了基于出租车充电OD对需求以最小行驶总距离为目标的优化模型,约束条件为总成本(包括建设费用和充电桩费用)和出租车到站没有空闲充电桩的概率均满足规划要求,即
2 求解算法
模型(5)—模型(12)属于非线性的整数规划问题,采用传统的启发式整数优化方法求解较为困难。本文采用遗传算法进行求解。该算法是简单的智能算法,其原理不再赘述。具体步骤如下。
Step 1:输入参数。初始选址数量g,运用Floyd算法,根据路段矩阵求出距离矩阵和路由矩阵。
Step 2:初始化。建立种群大小J、交叉率、变异率和最大种群代数K,置个体代号m=1,并依据∑Ji=1xi=g,随机产生M个初始种群 Sm=x1,x2,x3,…,xJ。
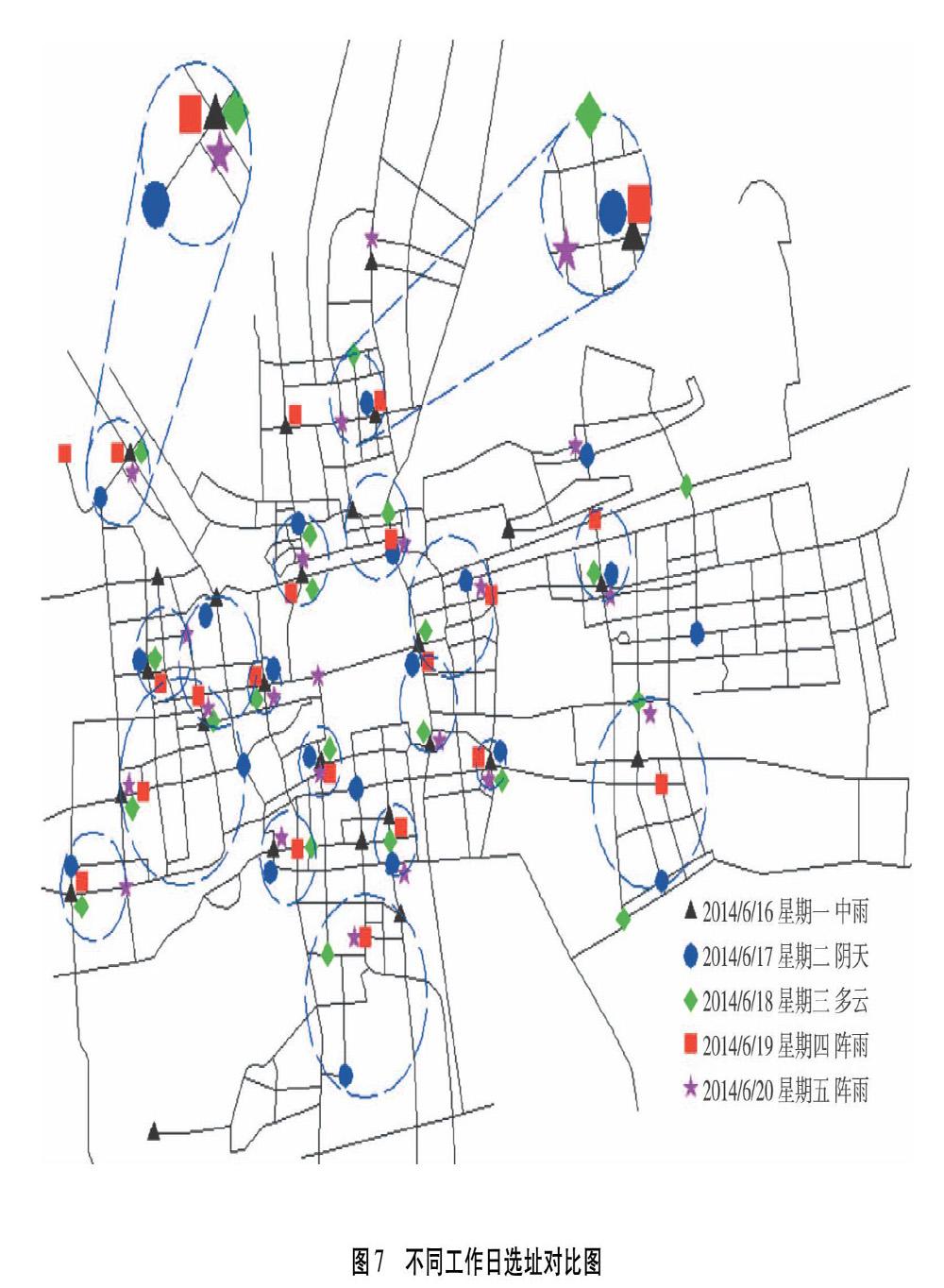
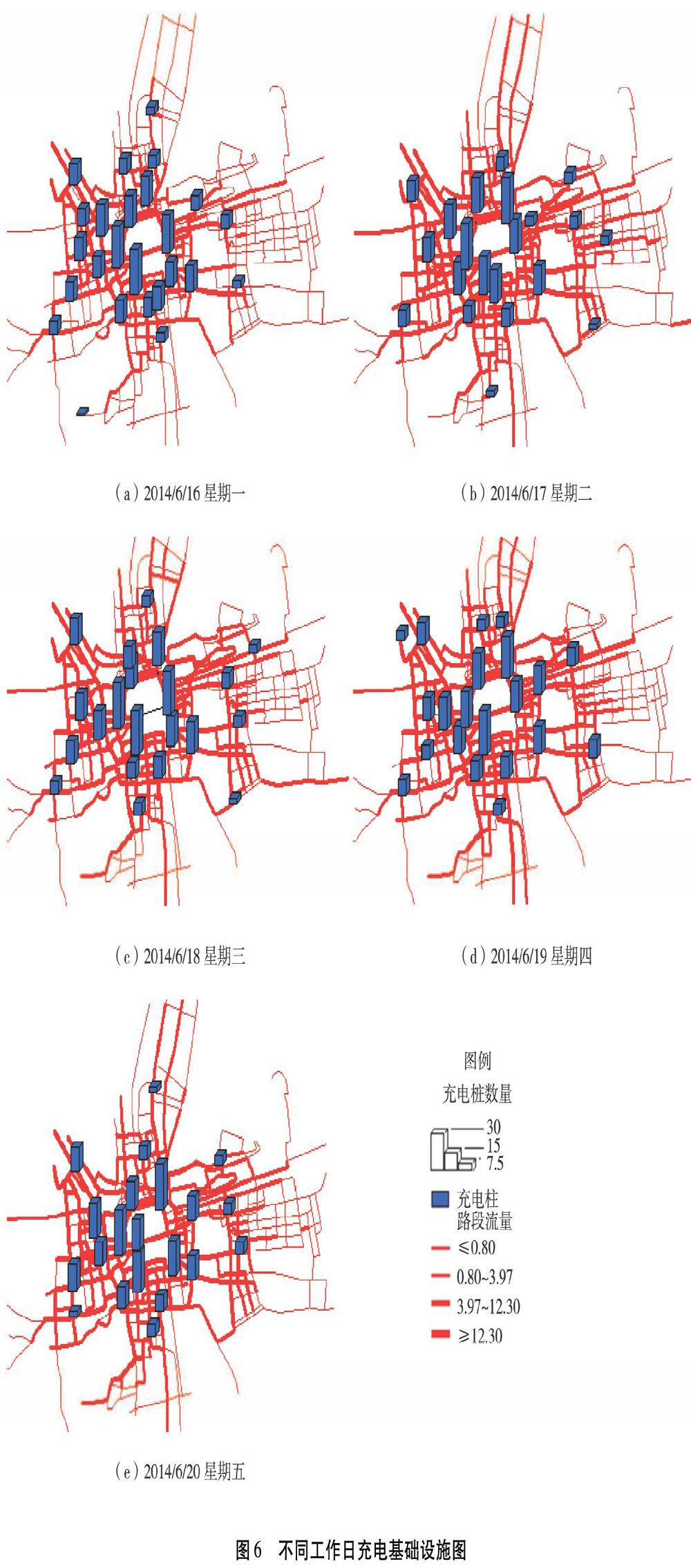
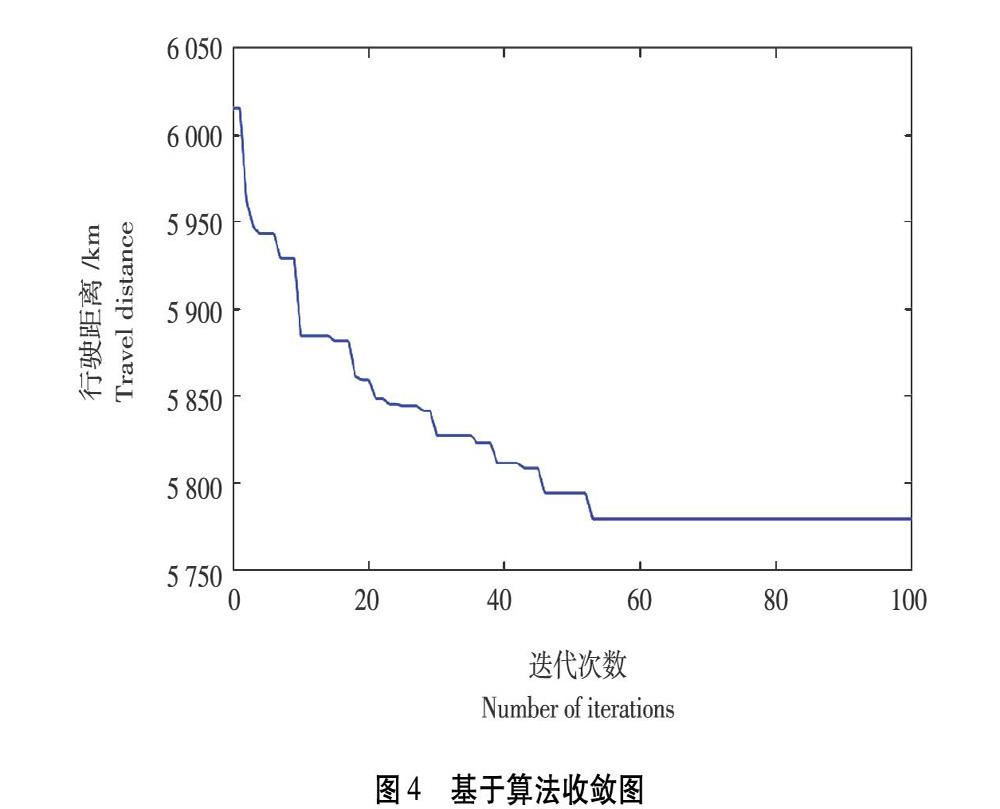
Step3:依据公式(5)计算各种群目标函数最小行驶总距离ZSm,并根据目标函数计算各种群的适应度FSm,用公式(13)计算,其中ε为适应度淘汰指数。
Step 4 :如果k Step5 :根据公式(4)及Step 4的Sm计算λj,j∈V。通过遍历确定满足公式(7)—公式(12)约束条件的充电桩数量可行解空间Λg。如果可行解空间Λg存在,则g=g+1,返回Step 2;如果可行解空间Λg不存在,则g=g-1,得到选址点集合Sg,可行解空间Λg,进行Step 6。 Step6:即Sg为最优解选址。可行解空间Λg中可行解最小成本即为充电桩最优解。 3 实例分析 将常规出租车的GPS数据作为插电式出租车的需求,开展充电站选址及充电设施的配置研究。根据2014年6月16日至2014年6月22日的中国苏州出租车GPS数据对充电需求进行估算,有效数据总共有1 125 136条,其中:16号153 463条数据、17号156 819条数据、18号157 118条数据、19号158 228条数据、20号168 192条数据、21号172 986条数据、22号158 330条数据。其中一条数据主要包括出租车OD对起讫点经纬度、时间、行程和车牌号等。 3.1 数据处理 首先根据A4的假设,把出租车GPS数据转换成充电OD对需求。充电OD对需求经纬度及研究区域主要道路网数据可视化,如图1所示。由图1可见,黑色为路网(包括461个结点和723个路段),紫色点为充电OD对需求起讫点。把研究区域划分成1 km×1 km的方格网小区(总共7 654个小区),见灰色方格网。把出租车充电OD对需求起讫点进行方格网聚集,得到划分小区的OD对矩阵。 根据路网将方格网小区的OD对矩阵进行分配,得到路网节点的OD对矩阵。出租车充电OD对需求将在O到充电站和充电站到D之间进行2次最短路径的选择,按照全有全无的規则分配到道路网络上去。 由于出租车GPS记录了出租车每天的订单起讫点数据。为了确保电动出租车能满足出行需求,有必要分析出租车需求受到气象、不同工作日的影响情况。为此,选取2014年6月16日至2014年6月22日一周的数据进行分析,如图2所示。由图2可知,2014年6月6日(星期一)有中雨,在16:00—19:00订单量基本上为零;2014年6月19日(星期四)和2014年6月20日(星期五)有阵雨,分别在1时和18时的订单量很小。由此可见,降雨量对出租车订单有影响,降雨量越大实际上会减少乘客对出租车的需求;由于星期六和星期天是周末,GPS数据缺失一部分,所以忽略对周末的数据进行分析。工作日每天的出租车订单数量趋于稳定,在8:00—10:00和20:00—23:00是订单高峰时段,符合居民出行的特点。 由订单分析结果忽略周末数据,根据假设A4和不同工作日的数据进行处理,为了解不同工作日电动出租车充电需求数量进行对比分析,选取2014年6月16日(星期一)至2014年6月20日(星期五)的数据分析。根据图3进一步验证了,降雨量对出租车订单有影响,降雨量越大实际上会减少出租车出行;且发现图2与图3形状相反,在6:00—8:00是充电的高峰期与运营高峰期相差1 h,其符合出租车充电和运营的特点。 3.2 结果分析 选取2014年6月16日6:00—8:00的出租车充电OD对需求进行分析,根据特斯拉的充电站建设指标[20],充电桩充电速率μ=1(车/h),出租车去充电站有空闲充电桩的最小概率η=0.9,充电站建设成本cs=200万元、一个充电桩的成本为ck=2万元,投资总成本为C=6 000万元。图4为求解算法的收敛结果,随着迭代次数的增加行驶总距离减少,其迭代50多次就达到最优值,说明迭代收敛快且迭代过程符合算法设计要求。 随着充电技术的进步将充电时间缩短,这将对电动出租车充电系统规划产生重要影响。由图5可知,在充电速率μ=1(车/h)时,行驶距离为5 725 km,系统内的充电站数量为21个;而μ=2(车/h)时,系统最小行驶距离为5 660 km,系统内的充电站数量为25个。由此可见,随着充电速率的增加,由于电动出租车充电需求所需的单位成本降低,将有更多的资金建设更多的充电站,由此减少出租车充电的行驶总距离。因此,充电技术的进步将直接提高整个充电设施的运营效率。 具体分析不同工作日出租车GPS数据对充电基础设施的影响。图6是关于不同工作日的充电站选址、路网中的路段流量及充电站中充电桩数量的结果,红色路段宽度表示路段出租车的流量,柱状图所在位置为充电站的选址点,蓝色代表充电桩数量。由图6可知,模型求解结果确保了充电站设置在路段需求流量大的路网节点,且在路网上的分布较均匀;另外,利用各个工作日的出租车大数据,对比相同位置充电站的充电桩数量大致相同。结合图6和图1进行分析得充电站选址综合考虑了流量大的区域及城市外围区域,并满足整个城市出租车的充电需求。 为了分析不同工作日充电站的选址结果,图7给出了不同工作日充电站选址。由图7可知,发现充电站在不同工作日的选址大致出现在同一区域,各个选址点相差1到2个交叉口的距离,其充电站选址呈簇状分布。这一结果表明,即使各个工作日的出租车需求存在随机性,但是模型利用这些大数据优化的选址区域是确定的,具体的结果区域内可能相差2 km左右(见图7中的放大部分)。因此模型结果具有相当的稳健性。对于城市布设充电站时,由于不是每个区域都能布设充电站,其充电站选址呈簇状分布,说明偏移一定距离其选址也符合出租车充电OD对需求,能够解决城市某些区域不能布设充电站的问题。 4 结束语 根据出租车乘客起讫点大数据估计充电OD对需求,基于M/M/K排队理论建立了描述出租车充电的随机模型,及出租车最小行驶总距离为目标的充电站选址及充电桩配置一体化优化模型,并运用遗传算法对模型进行求解。利用苏州市出租车GPS大数据对所建模型进行了验证。研究发现:随着充电速率的增加,将减少电动出租车充电需求的单位成本,从而增加充电站设站数量,由此将缩短电动出租车充电的行驶距离;基于不同工作日大数据求解的充电站选址在道路网中呈簇状分布。这表明基于运营大数据的电动出租车充电站选址优化结果具有稳健性。 研究成果将为充电站选址规划和充电桩的数量提供决策依据。基于运营大数据的插电式出租车充电设施优化模型,还可以进一步拓展以下方面的研究:①本研究仅考虑了出租车不受社会交通流的影响,该假设较为严格,在未来的研究中可以放松该假设,将道路交通流的实际影响考虑进来。②本研究并未考虑地价,只是统一用建设成本表示,不同的区域位置地价成本不一样。③在实际中,电动出租车充电需要充电位,且充电位及等待充电位的数量将影响电动出租车的充电情况。因此未来可针对该情形进行深入讨论。 【参 考 文 献】 [1]2018年全球电动汽车保有量及市占率走势分析预测[EB/OL].中国产业信息网, http://www.chyxx.com/industry/201806/648847.html.2018-6-12. Analysis and forecast of global electric vehicle ownership and market share trend in 2018[EB/OL]. http://www.chyxx.com/industry/201806/648847.html.2018-6-12. [2]HAKIMI S L. Optimum locations of switching centers and the absolute centers and medians of a graph[J]. Operations Research, 1964, 12(3): 450-459. [3]HAKIMI S L. Optimum distribution of switching centers in a communication network and some related graph theoretic problems[J]. Operations Research, 1965, 13(3): 462-475. [4]CHURCH R, REVELLE C. The maximal covering location problem[J]. Papers of the Regional Science Association, 1974, 32(1): 101-118. [5]SHAHRAKI N, CAI H, TURKAY M, et al. Optimal locations of electric public charging stations using real world vehicle travel patterns[J]. Transportation Research Part D: Transport and Environment, 2015, 41: 165-176. [6]GHAMAMI M, ZOCKAIE A, NIE Y M. A general corridor model for designing plug-in electric vehicle charging infrastructure to support intercity travel[J]. Transportation Research Part C: Emerging Technologies, 2016, 68: 389-402. [7] LI Y H, LUO J, CHOW C Y, et al. Growing the charging station network for electric vehicles with trajectory data analytics[C]// 2015 IEEE 31st International Conference on Data Engineering, Seoul, South Korea, IEEE, 2015. [8]WONG R C P, SZETO W Y, WONG S C. A cell-based logit-opportunity taxi customer-search model[J]. Transportation Research Part C: Emerging Technologies, 2014, 48:84-96. [9]DASKIN M S. Location modeling in perspective[J]. Wiley Online Library, 1995: 383-400. [10]TU W, LI Q Q, FANG Z X, et al. Optimizing the locations of electric taxi charging stations: a spatial-temporal demand coverage approach[J]. Transportation Research Part C: Emerging Technologies, 2016, 65: 172-189. [11]HU L, DONG J, LIN Z H, et al. Analyzing battery electric vehicle feasibility from taxi travel patterns: The case study of New York City, USA[J]. Transportation Research Part C: Emerging Technologies, 2018, 87: 91-104. [12]JUNG J, CHOW J Y J, JAYAKRISHNAN R, et al. Stochastic dynamic itinerary interception refueling location problem with queue delay for electric taxi charging stations[J]. Transportation Research Part C: Emerging Technologies, 2014, 40: 123-142. [13]ASAMER J, REINTHALER M, RUTHMAIR M, et al. Optimizing charging station locations forurban taxi providers[J]. Transportation Research Part A: Policy and Practice, 2016, 85: 233-246. [14]CAI H, JIA X P, CHIU A S F, et al. Siting public electric vehicle charging stations in Beijing using big-data informed travel patterns of the taxi fleet[J]. Transportation Research Part D: Transport and Environment, 2014, 33: 39-46. [15]LU C C, YAN S Y, HUANG Y W. Optimal scheduling of a taxi fleet with mixed electric and gasoline vehicles to service advance reservations[J]. Transportation Research Part C: Emerging Technologies, 2018, 93: 479-500. [16]KANG S C, LEE H. Economic appraisal of implementing electric vehicle taxis in Seoul[J]. Research in Transportation Economics, 2019, 73: 45-52. [17]GROSS D, SHORTIE J F, THOMPSON J M, et al. Fundamentals of queueing theory[M]. John Wiley & Sons, 2008. [18]WANG N, LIU Y F, FU G Z, et al. Cost-benefit assessment and implications for service pricing of electric taxies in China[J]. Energy for Sustainable Development, 2015, 27: 137-146. [19]CHRYSOSTOMOU K, GEORGAKIS A, MORFOULAKI M, et al. Using big taxi GPS data to investigate the feasibility of electric taxis in Thessaloniki, Greece[C]// 95th Annual Meeting of the Transportation Research Board (TRB), Washington DC, United States, 2016. [20]GUO M. How much does it cost to build an electric car charging station[EB/OL]. http://www.chinairn.com/scfx/20180608/11400154.shtml. 2018-6-8.
