森林防火机器人轨迹寻踪技术研究
2020-05-28布升强梅淼李琼琼杨家富王大明
布升强 梅淼 李琼琼 杨家富 王大明

摘 要:蚁群算法是解决森林防火机器人轨迹寻踪问题的有效方法,针对传统蚁群算法收敛速度慢、容易陷入局部最优解的不足,本文设计一种自适应的蟻群算法。信息素启发因子α与期望启发因子β共同起引导蚂蚁搜索的作用,动态调整两者在搜索过程中的取值,提高收敛速度;基于地图位置信息设计改进型的启发式函数,提高前期搜索效率;依据蚂蚁的行进意图扩展禁忌表内容,避免路径交叉,减少蚂蚁的迷失数量;在信息素更新函数中导入转角指标,并通过信息素浓度对比试验确定权重系数的最优取值,使路径更平滑;基于Matlab平台搭建林区仿真地图,对比测试自适应蚁群算法性能。试验结果表明,自适应蚁群算法具有自适应调节能力、不会出现交叉路径,与传统蚁群算法相比,在收敛速度与搜索结果方面有着较好的改善。
关键词:森林防火机器人;蚁群算法;轨迹寻踪
Abstract:Ant colony algorithm is an effective method to solve the problem of track tracking of forest fire protection robot. Aiming at the shortcomings of traditional ant colony algorithm, such as slow convergence speed and easy to fall into the local optimum, an adaptive ant colony algorithm is proposed in this paper to solve these problems. Pheromone heuristic factor α and expectation heuristic factor β work together to guide the ant search. To accelerate the convergence rate, the value of α and β in the search process is dynamically adjusted. The heuristic function based on the information of location is designed to improve the efficiency of early ant search. Based on ants intention, the tabu table is expanded to avoid path crossing and reduce the number of lost ants. The corner performance index is added to the update function of pheromone to smooth the search path, and the optimal value of the weight coefficient is determined by the contrast test of pheromone concentration. The simulation map of forest region is built based on Matlab, and the performance of adaptive ant colony algorithm is. Experimental results show that the algorithm has the ability of self-adaptive adjustment, and does not appear cross path. Compared with the traditional ant colony algorithm, the algorithm has better convergence speed and better search results.
Keywords:Forest fireproof robot; ant colony algorithm; track tracing
0 引言
森林火灾是一种突发性强、破坏力大的自然灾害。森林火灾事发突然,蔓延速度快,火灾的扑灭也显得格外困难。及时发现和清理隐燃的余火,特别是肉眼难以发现的无烟隐燃火,才能够有效地避免发生余火复燃。长期以来,一直采用人工进行森林余火探测与清理,该方式效率低下并且危险系数很高。为了提高探测余火的效率和安全系数,需要一种有效的、快速的余火探测及清理移动消防机器人,该消防机器人能够在森林地形条件下进行火灾探测和清理等消防作业[1-4]。本文主要讨论在全局环境信息已知的基础上,林区防火机器人的轨迹寻踪研究。
轨迹寻踪技术是人工智能领域中的一个重要分支,主要用于引导移动机器人在已知环境内快速搜索出一条从起始点与到目标点的可行路径。轨迹寻踪的算法大致可分为:基于势场的搜索算法[5-6],基于采样的搜索算法[8-9],基于仿生学的搜索算法[7]。其中,基于势场的搜索算法与基于采样的算法优点在于能够在短时间内快速搜索出可行路径,缺点是在大范围复杂路况下搜索时,易陷入局部最优甚至导致搜索失败。相比之下,基于仿生学的搜索算法,能有效地求解出路径最优解,并表现出良好的自组织、自管理能力。本文选用基于仿生学的搜索算法作为该环境下的轨迹寻踪算法。
在基于仿生学的搜索算法中,最具代表性的有蚁群算法(ACO)、粒子群算法(PSO)、细菌觅食法(BFO)、人工蜂群算法(ABC)和萤火虫算法(FA)等,其中,蚁群算法(ACO)的启发机制与反馈机制能保证算法的可靠性[10-13],但传统的蚁群算法存在收敛速度过慢和易陷入局部最优点等不足。针对基本蚁群算法的这些缺点,国内外学者们进行了相关研究,并提出了大量的改进方法,改进的思想可分为两类:第一类是围绕蚁群算法自身的结构和参数进行优化,结构优化的思想主要有最大最小蚁群系统[14-17]、精英蚂蚁优化策略[18]和双向搜索策略[19]等,参数优化的思想主要包括多要素的启发式搜索策略[20]、带赏罚机制的搜索策略[21]等;第二类是多算法融合的优化思想,如多群落混合的搜索策略[22]、模拟退火的搜索策略[23]等。
林区环境中存在的障碍物种类主要以静态障碍物为主,可将林区环境视为具有复杂路况的地图。本文主要基于第一类优化思想设计了自适应的蚁群算法,包括混合型的启发式函数与复合型的信息素更新策略的设计,以及两者权重系数的动态调整,同时扩增了禁忌表的内容。
1 传统蚁群算法
蚁群算法最初由意大利学者Marco Dorigo等于1991年提出[7]。在求解路径规划问题中,计算可行路径处的转移概率pmi,j(t),根据轮盘赌法选择蚂蚁下一步的移动位置。
转移概率pmi,j(t)的具体公式为:
2 自适应改进型蚁群算法
2.1 参数α、β基于迭代次数的自适应改进
迭代初期,各路径上的信息浓度大致相同,启发式信息在搜索过程起引导作用。随着算法迭代,路径上的信息素逐渐累积,信息素替代启发式信息在搜索过程中起引导作用。当某一路径上的信息素浓度远超过其他路径上的信息素浓度时,为防止蚂蚁因信息素累积而陷入局部最优解的情况,需要减弱信息素的作用。由上述分析得出,α在迭代過程中呈现先增后减的变化趋势,而β的变化趋势与α“互锁”,即先减后增的变化趋势。在传统的蚁群算法中,α和β通常取某个固定值,算法缺乏自适应能力。为描述参数α与β在迭代过程中的变化趋势,本文选用幅度衰减的三角函数,见公式(3)和公式(4)。在不改变其他参数的基础上,测试衰减幅度对算法性能的影响,见表1。当衰减程度为30%,搜索效果较好。
2.2 混合改进型启发式函数
启发式函数可视为搜索导向信息,引导蚂蚁的搜索。传统蚁群算法中,计算当前位置距离终点的最短距离,取该距离的倒数作为启发式函数的取值,见公式(5)和公式(6)。这是一种贪心策略,蚂蚁会因贪图当前路径而错过全局最优路径,且容易在复杂路况下迷失。
2.3 信息素更新策略
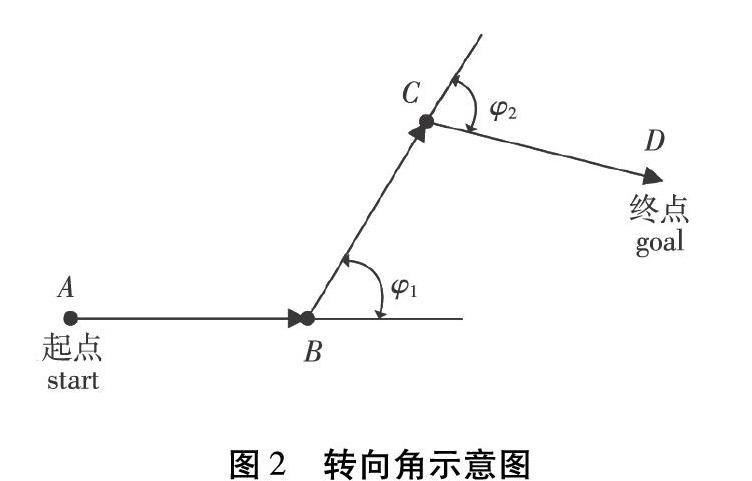
蚁群算法中,更新信息素的方法[6]主要有:Ant-Cycle模型、Ant-Density模型和Ant-Quantity模型。传统的蚁群算法常选择Ant-Cycle模型作为信息素的更新策略,但是Ant-Cycle模型仅考虑路径的最短距离,忽略了路径的平滑程度。在机器人的应用领域,需要考虑转弯角度的影响,因此本研究加入了转角θcost指标,要求机器人搜索出一条转角有限的平滑路径。如图2所示,A、B、C、D为路径节点,start、goal则对应路径的起点、终点,路径的转向角分别为φ1与φ2。
2.4 禁忌表优化
传统的蚁群算法中,为避免蚂蚁重复搜索,蚂蚁在确定移动位置后,便将当前位置加入禁忌表中,后续的蚂蚁在选取移动路径时,会参考禁忌表中的信息,避免出现“倒退”的情况,但“不倒退”的策略在面对“凹陷”的区域时,容易迷失在其中。蚂蚁在“凹陷”区域内搜索路径,常会出现路线“相交”的情况。本文将“相交”路径视为蚂蚁陷入“凹陷”区域的标志,在此基础上,把上一位置的邻域加入禁忌表中以改善路径“相交”的情况。
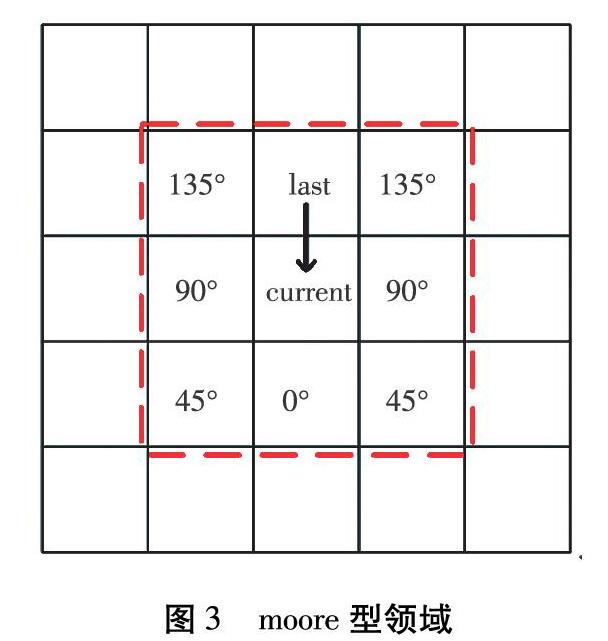
根据蚂蚁移动情况,将蚂蚁“后方”的位置加入禁忌表,确保蚂蚁“前向”选择路径,图4与图5表示蚂蚁往某一方向直行或转弯后可行路径的情况,在原始禁忌表的基础上,将起始栅格(is,js)的相邻点(is+signi,js+signj)加入禁忌表,其中signi与signj为位置增量标志,根据蚂蚁具体的行进情况取值0、1。
3 仿真实验
常见的地图模型有:拓扑地图、栅格地图和四叉树模型等,其中栅格地图实现与维护简单,常用于表示环境信息。本研究采用栅格法建立二维的地图模型,林区存在的障碍物大多形状不规则且分布不均,需对栅格地图中的障碍物膨胀处理直至填满栅格并记为1。
3.1 地图模型
本研究采用栅格法建立二维的地图模型,地图中的栅格位置通过序号法表示,见公式:
3.2 算法流程
蚁群算法的参数选取一般根据经验取值,并通过实验择优。迭代次数与蚂蚁数量的取值过小影响算法的收敛结果,取值过大时效性差,通常将蚂蚁数量设置为30~50只、迭代为100~150次。为突显信息素对搜索过程的影响,蒸发系数设置为0.2~0.5。本研究选用20×20的栅格地图,参数取值见表2。
3.3 结果分析
在20×20的栅格地图上,分别测试原始蚁群算法,尤海龙等[7]基于迭代次数改进的蚁群算法(以下简称为改进蚁群算法),本文的自适应蚁群算法(以下简称为自适应蚁群算法)。对比测试不同算法间的差异,由于蚂蚁遵循赌轮盘法的规则选取路径,算法存在一定的随机性,每一次执行都可能得出不同的结果,因此,重复试验10次,并记录平均值。
(1)障碍物随机分布地图下的仿真实验
在20×20的栅格地图上,通过随机函数生成障碍物的分布情况,设置障碍物数量占栅格总数量的35%。在此情况下,重复多次试验并对所得试验结果取均值。3种算法的路径性能指标的对比结果见表3,路线情况如图7所示。
在表3中,蚂蚁迷失率等于搜索失败的蚂蚁数量比蚂蚁的总数量,迭代稳定次数取决路径收敛的最小迭代次数并取整。结果表明,3种算法的搜索路径长度相差不大,对比其余路径指标,自适应蚁群算法与改进算法均优于原始算法。自适应蚁群算法与改进算法在迷失率和迭代稳定次数上差距不大,但在运行时间上自适应蚁群算法优化了8.9%。
在图6中,圆形标记代表本文的自适应蚁群算法,菱形标记代表改进蚁群算法,方形标记代表原始算法,3种算法的后半程搜索路线情况基本一致,差别集中在前半程路径。自适应蚁群算法的搜索路径在光滑程度方面要优于传统算法与改进蚁群算法。由图7可知,自适应蚁群算法与改进蚁群算法的收敛情况均优于原始算法,同时,自适应蚁群算法的收敛次数与最小路径长度皆优于改进蚁群算法。
4 結束语
根据森林防火机器人的轨迹寻踪需求,基于原始蚁群算法,提出了一种自适应的蚁群算法。为降低蚂蚁前期搜索的盲目性,在启发式函数中加入了位置分布信息,引导蚂蚁在搜索前期有针对性地进行搜索,提高了算法的收敛速度;动态调整α、β两种参数的取值,优化了算法的自适应能力;在信息素更新函数中导入转角指标,要求蚂蚁搜索出一条转角较少的平滑路径,同时验证了转角指标对信息素浓度分布的影响;扩增了禁忌表的内容,以确保蚂蚁前向搜索,有效地回避交叉路径;在仿真试验平台下,验证了算法的可行性与有效性,为森林防火机器人的轨迹寻踪技术提供了理论基础,但是本文主要针对静态环境下复杂路径规划的研究,在动态性能方面,算法的搜索效率不高,还有待进一步的研究。
【参 考 文 献】
[1]蒋敬, 郭会玲, 蒋霄然. 我国2005—2016年森林火灾案件大数据分析[J]. 林业经济, 2019, 41(7): 106-109.
JIANG J, GUO H L, JIANG X R. Big data analysis on chinas forest fire cases from 2005 to 2016[J]. Forestry Economics, 2019, 41(7): 106-109.
[2]邸雪颖, 刘畅, 孙建, 等. 森林火灾损失评估技术研究[J]. 森林工程, 2015, 31(2): 42-45.
DI X Y, LIU C, SUN J, et al. Technical study on forest fire loss assessment[J]. Forest Engineering, 2015, 31(2): 42-45.
[3]魏娜,肖冰,才丽华,等.基于GIS的森林安全防火系统的研究[J].林业机械与木工设备,2019,47(12):16-19.
WEI N, XIAO B, CAI L H, et al. Research on forest safety fire prevention system based on GIS[J]. Forestry Machinery & Woodworking Equipment, 2019, 47(12):16-19.
[4]陈越, 赵亚琴, 蒋林权,等. 森林火灾火焰像素检测的背景减除算法[J]. 林业工程学报, 2018, 3(4):131-136.
CHEN Y, ZHAO Y Q, JIANG L Q. Background subtraction algorithms for detecting flame pixels of forest fire[J]. Journal of Forestry Engineering, 2018, 3(4):131-136.
[5]刘志荣, 姜树海. 基于强化学习的移动机器人路径规划研究综述[J]. 制造业自动化, 2019, 41(3):90-92.
LIU Z R, JIANG S H. Review of mobile robot path planning based on reinforcement learning[J]. Manufacturing Automation, 2019, 41(3): 90-92.
[6]施杨洋,杨家富,布升强,等. 基于RRT改进的智能车辆路径规划算法[J]. 计算技术与自动化, 2019, 38(4): 143-148.
SHI Y Y, YANG J F, BU S Q, et al. Improved intelligent vehicle pathing planning algorithm based on RRT[J]. Computing Technology and Automation, 2019, 38(4): 143-148.
[7]尤海龙, 鲁照权. 参数α、β和ρ自适应调整的快速蚁群算法[J]. 制造业自动化, 2018, 40(6): 99-102.
YOU H L, LU Z Q. A fast ant colony algorithm for α, β and ρ adaptive adjustment[J]. Manufacturing Automation, 2018, 40(6): 99-102.
[8]张玮, 马焱, 赵捍东, 等. 基于改进烟花-蚁群混合算法的智能移动体避障路径规划[J]. 控制与决策, 2019, 34(2): 335-343.
ZHANG W, MA Y, ZHAO H D, et al. Obstacle avoidance path planning of intelligent mobile based on improved fireworks-ant colony hybrid algorithm[J]. Control and Decision, 2019, 34(2): 335-343.
[9]RAJPUT U, KUMARI M. Mobile robot path planning with modified ant colony optimisation[J]. International Journal of Bio-Inspired Computation, 2017, 9(2): 106.
[10]PATLE B K, BABU L G, PANDEY A, et al. A review: On path planning strategies for navigation of mobile robot[J]. Defence Technology, 2019, 15(4): 582-606.
[11]康冰, 王曦辉, 刘富. 基于改进蚁群算法的搜索机器人路径规划[J]. 吉林大学学报(工学版), 2014, 44(4): 1062-1068.
KANG B, WANG X H, LIU F. Path planning of searching robot based on improved ant colony algorithm[J]. Journal of Jilin University (Engineering and Technology Edition), 2014, 44(4): 1062-1068.
[12]卜新苹, 苏虎, 邹伟, 等. 基于复杂环境非均匀建模的蚁群路径规划[J]. 机器人, 2016, 38(3): 276-284.
BU X P, SU H, ZOU W, et al. Ant colony path planning based on non-uniform modeling of complex environment[J]. Robot, 2016, 38(3): 276-284.
[13]黄艳国,宋峰华.遗传蚁群算法在公路隧道照明设计中的应用[J].公路工程,2018,43(4):39-43.
HUANG Y G, SONG F H. Application of genetic ant colony algorithm in lighting design of highway tunnel[J]. Highway Engineering, 2018, 43(4):39-43.
[14]BANERJEE A, CHATTOPADHYAY S, GHEORGHE G, et al. Minimization of reliability indices and cost of power distribution systems in urban areas using an efficient hybrid meta-heuristic algorithm[J]. Soft Computing, 2019, 23(4): 1257-1281.
[15]刘建华, 杨建国, 刘华平, 等. 基于势场蚁群算法的移动机器人全局路径规划方法[J]. 农业机械学报, 2015, 46(9): 18-27.
LIU J H, YANG J G, LIU H P, et al. Robot global path planning based on ant colony optimization with artificial potential field[J]. Transactions of the Chinese Society for Agricultural Machinery, 2015, 46(9): 18-27.
[16]宋广虎,冯全,海洋,等.采用深度学习法优化的葡萄园行间路径检测[J].林业机械与木工设备,2019,47(7):23-27.
SONG G H,FENG Q,HAI Y,et al.Vineyard Inter-row Path Detection Based on Deep Learning[J].Forestry Machinery & Woodworking Equipment,2019,47(7):23-27.
[17]王曉燕, 杨乐, 张宇, 等. 基于改进势场蚁群算法的机器人路径规划[J]. 控制与决策, 2018, 33(10): 1775-1781.
WANG X Y, YANG L, ZHANG Y, et al. Robot path planning based on improved ant colony algorithm with potential field heuristic[J]. Control and Decision, 2018, 33(10): 1775-1781.
[18]方朋朋, 杨家富, 施杨洋, 等. 基于梯度下降法和改进人工势场法的无人车避障方法[J]. 制造业自动化, 2018, 40(11): 81-84.
FANG P P, YANG J F, SHI Y Y, et al. Gradient descent method and improved artificial potential field method for obstacle avoidance of unmanned vehicle[J]. Manufacturing Automation, 2018, 40(11):81-84.
[19]DAI X L, LONG S, ZHANG Z W, et al. Mobile robot path planning based on ant colony algorithm with A* heuristic method[J]. Frontiers in Neurorobotics, 2019, 13: 15.
[20]TAHERI E, FERDOWSI M H, DANESH M. Closed-loop randomized kinodynamic path planning for an autonomous underwater vehicle[J]. Applied Ocean Research, 2019, 83: 48-64.
[21]YUE L W, CHEN H N. Unmanned vehicle path planning using a novel ant colony algorithm[J]. EURASIP Journal on Wireless Communications and Networking, 2019, 2019(1): 136.
[22]孙琼, 李林. 旅游路线规划蚁群算法的伪随机比例规则优化[J]. 科技通报, 2016, 32(1): 175-178.
SUN Q, LI L. Optimized pseudo-random proportion rule of ant colony algorithm for tourist routes planning[J]. Bulletin of Science and Technology, 2016, 32(1): 175-178.
[23]CASTILLO O, NEYOY H, SORIA J, et al. A new approach for dynamic fuzzy logic parameter tuning in Ant Colony Optimization and its application in fuzzy control of a mobile robot[J]. Applied Soft Computing, 2015, 28: 150-159.
